Chose promie, chose due:
Je vais tenter une explication complète avec la molécule d'azote N2 comme exemple. Elle n'a pas trop d'électrons, en a quand même plus que H2 et n'a pas la particularité de l'état fondamental triplet de O2. 
Un atome isolé d'azote N a la configuration électronique suivante: 1s2 2s2 2p3 ou plus précisément 1s2 2s2 2px1 2py1 2pz1 (=orbitales atomiques).
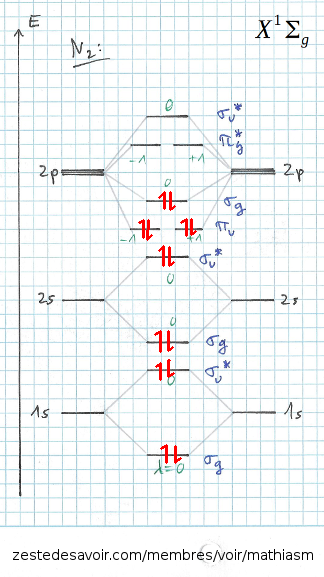
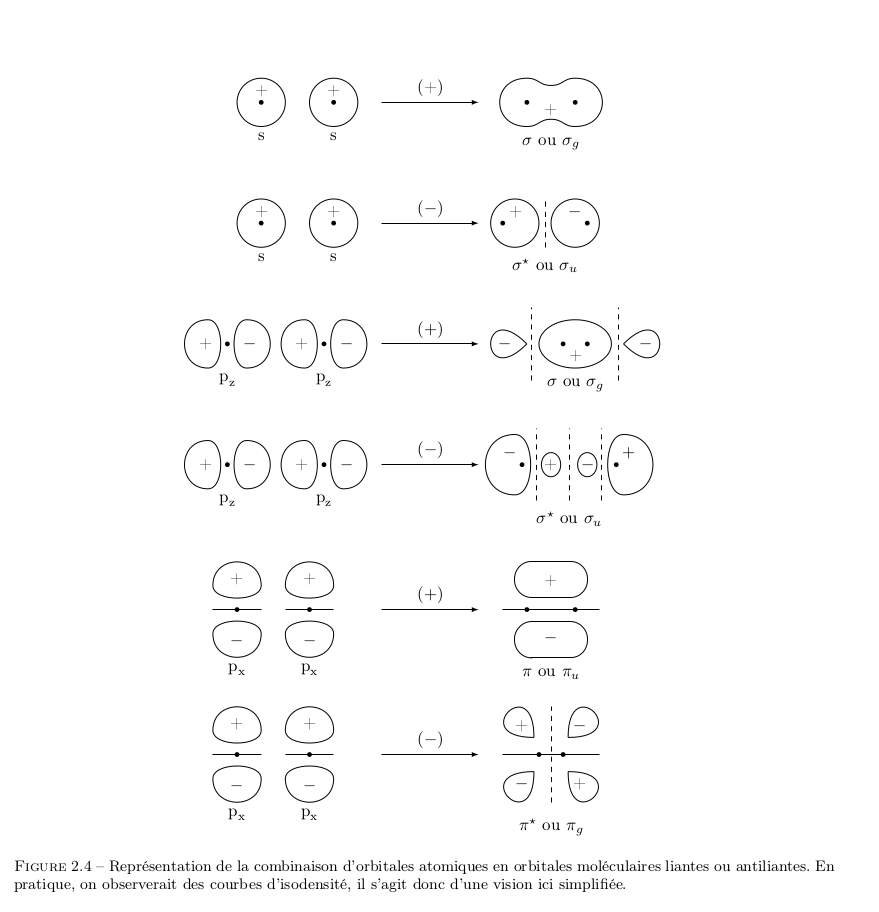
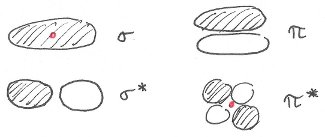
Dans une molécule d'azote N2, ces orbitales atomiques (AOs) forment des orbitales moléculaires (MOs) $\sigma$ et $\pi$. Quelques conventions: si l'orbitale est anti-liante, elle porte l'exposant *. Si l'orbitale possède un centre d'inversion i, elle porte un indice g; si elle ne possède pas de centre d'inversion, elle porte l'indice u. Voici donc le diagramme des MOs:
(on constate que les 2 orbitales $\pi_u$ sont plus basses en énergie que la $\sigma_g$, c'est une spécificité de N2 à savoir)
Dans le diagramme de MOs ci-dessus, j'ai déjà placé les 14 électrons de la molécule en partant du bas et en suivant le principe d'exclusion de Pauli, ce qui donne l'état fondamental.
Le terme spectroscopique suit les normes suivantes:
{X,A,B,…}{1,3}{$\Sigma$,$\Pi$,…}{g,u}
- X signifie "état fondamental", A "1er état excité", etc.
- l'exposant 1 ou 3 indique si l'état est singulet ou triplet
- le symbole grec indique la valeur absolue de la somme des moments angulaires $\lambda$ pour chaque électron ($\Sigma$ pour une somme de 0, $\Pi$ pour 1). Les moments angulaires valent $\lambda=0$ pour les MOs $\sigma$, $\lambda=-1$ pour les $\pi$ de gauche et $\lambda=1$ pour les $\pi$ de droite.
- g ou u se détermine en faisant le produit total des u/g pour chaque électron avec les règles de multiplication suivantes: gxg=g, uxu=g, gxu=u
Donc pour l'état fondamental ci-dessus, on a:
- état fondamental $\rightarrow$ X
- singulet $\rightarrow$ 1
- |0+0 + 0+0 + 0+0 + 0+0 + (-1)+(-1) + 1+1 + 0+0 | = 0 $\rightarrow$ $\Sigma$
- g g u u g g u u u u u u g g = g
Ce qui donne au final X1$\Sigma$g.
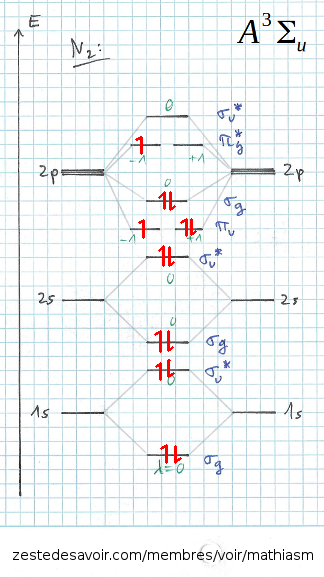
Le 1er état énergétique situé au-dessus de l'état fondamental est celui avec un électron situé dans la MO $\pi_g$* au lieu de la MO $\pi_u$ et est un état triplet (c'est un constat expérimental, il faut le savoir "par coeur" je crois):
Terme spectroscopique:
- 1er état excité $\rightarrow$ A
- triplet $\rightarrow$ 3
- | 0+0 + 0+0 + 0+0 + 0+0 + (-1) + 1+1 + 0+0 + (-1) | = 0 $\rightarrow$ $\Sigma$
- g g u u g g u u u u u g g g = u
Soit A3$\Sigma$u.
Le 2ème état excité est avec un électron dans la MO $\pi_g$* au lieu de la MO $\sigma_g$ et est un état triplet, le terme est B3$\Pi$g. Je vous laisse vérifier pour voir si vous avez compris!
Ce n'est pas parce que tous ces états excités existent que toutes les transitions entre eux sont permises!
J'espère que c'est désormais un peu plus clair pour vous? N'hésitez pas à demander pour plus de précisions. 
Le seul soucis d'après moi est de savoir l'ordre des excitations (d'ailleurs je suppose qu'on les obtient uniquement par expérience, mais je ne connais pas grand chose à ce domaine…). Mais à part ces A/B/…, vous devriez être capables de donner le terme spectroscopique pour tout diagramme rempli d'électrons.
Bonne chance!





 )
)