Calculer les k plus courts chemins dans un graphe

Bonjour,

Je vous propose un challenge d'algorithmique qui je l'espère va vous intéresser.

Mise en situation

Vous êtes invité à passer une soirée chez des amis. Rien de mieux pour commencer ce magnifique weekend d'été ! La soirée débute à 20H dans une salle qui vous est inconnue. Mais pas de panique, vous avez votre GPS et votre amis vous a donné l'adresse de la salle. Il est 19h30 et votre GPS vous indique qu'il vous faut 25mn pour vous rendre à votre soirée. Patatra ! Vous détestez par dessus tout arrivé à l'heure à une soirée, et arriver en avance serait encore pire ! Sauf que maintenant, vous êtes installé dans votre voiture et vous ne souhaitez pas en sortir. Vous voudriez que votre GPS vous donne un autre itinéraire un peu plus long, ainsi vous ne perdriez pas votre temps, et comme vous aimez rouler, cela ferait d'une pierre deux coups. Le problème c'est que votre GPS ne sait pas faire ça. Alors vous commencez à réfléchir à une solution pour ce problème…

Définition du problème

Le problème du plus court chemin est un problème bien connu en informatique. Etant donné un graphe et deux sommets $i$ et $j$ de ce graphe, vous cherchez le plus court chemin entre ces deux sommets. Généralement, une fonction $\varphi$ associe à chaque arc du graphe une valeur (en général un nombre réel). Le coût d'un chemin est alors définit comme la somme des coûts sur les arcs (donné par $\varphi$). Vous cherchez donc le chemin qui minimise ce coût.

Si vous avez fait un peu d'informatique, on sait facilement résoudre ce problème en utilisant des algorithmes comme Dijsktra ou Bellman-Ford.

Le challenge que je vous propose ici consiste non pas à calculer le plus court chemin mais les k plus courts chemins, k étant fixe (un paramètre de votre algorithme). Bien sûr, il va de soi que les chemins doivent être différents (mais ils peuvent avoir le même coût).

Votre algorithme prendra en entrée

• un graphe
• un entier $k$ qui indique le nombre de plus courts chemins à calculer
• un entier $i$ qui est le noeud de départ
• un entier $j$ qui est le noeud d'arrivé

Exemple

Afin de fixer les idées si on prend le graphe suivant :

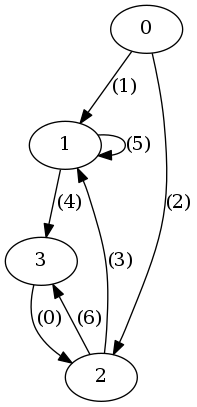
On suppose que votre noeud de départ est le noeud $0$. Vous vous intéressez à calculer les $2$ pluscourts chemins. Votre algorithme devra alors renvoyer les résultats suivants (ici ce sont les 2 plus courts chemins issus du sommet $0$) :

Par exemple le plus court chemin pour aller au sommet $2$ en partant de $0$ c'est en prenant l'arc $(0,2)$ de coût $2$. Mais si on cherche un itinéraire alternatif alors il existe un autre chemin qui vous fait passer successivement par les sommets $0,1,3,2$ dont le coût est $5$.

Pour le sommet $0$ c'est un peu particulier. Par convention, il existe un plus court chemin pour aller d'un noeud vers ce même noeud qui est de coût nul ($0$). Mais si vous cherchez, il n’existe pas d'autres chemins pour rejoindre le sommet $0$. Et donc le deuxième plus court chemin n’existe pas. Cela est représenté par le symbole $\infty$.

Quelques outils

Comme me l'a fait remarquer Davidbrcz, il serait bon de ma part de vous fournir des outils afin de vous faciliter la tâche. Malheureusement, je ne serai capable de vous aider que dans un langage particulier à savoir Ocaml. Cependant tout aide est la bienvenue ! Donc n'hésitez pas à proposer des squelettes de codes dans un langage particulier. J'ajouterais aussi que dans la plupart des langages, vous trouverez facilement une librairie de graphes pour vous faciliter la tâche.

Ocaml

Si vous comptez utiliser Ocaml, Jean-Christophe Filliâtre et Sylvain Conchon ont codé une très bonne librairie de graphe qui s'appelle sobrement ocamlgraph. Elle est très générique et peut-être déroutante de prime abord. On va voir par la suite comment s'en servir. Avant toute chose, si vous n'avez pas ocamlgraph, vous pouvez le télécharger par opam :

1

opam install ocamlgraph

Pour ne pas s'embêter à la compilation vous pouvez utiliser ocamlbuild (disponible sur opam également).

Pour ma part j'utilise un simple petit Makefile pour compiler mon projet qui ressemble à ça :

1
2

all:
    ocamlbuild -use-ocamlfind -package ocamlgraph main.native

Cela va compiler le fichier main.ml et toutes les dépendances qui vont avec. Si votre code est dans un autre fichier, veuillez changer le main.native par <nom_fichier>.native.

Ocamlgraph vous propose deux types de graphes: persistent ou imperative. Je privilégie les structures de données persistent car plus idiomatique à la programmation fonctionnelle. Pour connaître la différence, il vous suffit de regarder l'interface proposer par ocamlgraph.

Ensuite vous avez quatre types de graphes qui vous sont proposés. Je vous conseille d'utiliser le module ConcreteLabeled. Les sommets sont des int, mais vous pouvez donner un label à vos arc. Le label étant du type que vous souhaitez. Dans notre cas, ce type pourrait être un int ou autre chose en fonction de votre algorithme.

Entrées/sorties

En lisant la doc, vous verrez aussi qu'il existe le module Graphviz qui vous permet d'afficher un graphe. Mais pour afficher un graphe il faut pouvoir le créer. Pour ma part, j'ai utilisé un générateur. Cependant, afin d'avoir d'avoir un format compatible, il peut-être intéressant de lire un graphe au format .dot. Heureusement il existe un parser intégrer à la librairie ocamlgraph. Pour créer un graphe dans ce format, vous pouvez regarder ici (c'est très simple).

Snippet

Voici un code minimal qui vous montre comment créer le graphe d'exemple avec ocamlgraph

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

open graph
module Vertex = struct
  type t = int
  let compare = compare
  let hash = Hashtbl.hash
  let equal = (=)
end
      
module Edge = struct
  type t = int
  let compare = compare
  let default = 0
end

(* Kind of graph that we use*)
module Graph = Persistent.Digraph.ConcreteLabeled(Vertex)(Edge)


let _ =
  let g = Graph.empty in
  let edge = Graph.E.create 0 1 1 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 1 4 3 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 1 5 1 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 3 0 2 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 0 2 2 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 2 3 1 in
  let g = Graph.add_edge_e g edge in
  let edge = Graph.E.create 2 6 3 in
  let g = Graph.add_edge_e g edge in
  Printf.printf "Hello graph!");

Jeux d'essais

Si vous en faites la demande, je pourrais mettre des jeux d'essais au format dot qui est très facile à parser.

Mot de la fin

Voilà ! Il me semble que vous avez toutes les clés en main pour comprendre le problème et tenter de le résoudre. Si vous avez la moindre question, n'hésitez pas !

Bonne chance !

vers ce même noeud qui est de coup nul

coût. Mais sinon, le challenge a l'air intéressant, même si la question semble plus mathématique qu'informatique.

J'ai fait le choix de placer le problème dans un contexte pas trop général justement. Sinon, oui tu peux généraliser (assez facilement) et tomber dans de l'algèbre. Ce sera sans doute l'objet de quelques articles.

Il ne suffit pas d'appliquer des algorithmes de flots minimal / maximal de manière intelligente ?

Il y a plusieurs solutions possibles. Si tu en as une, vas-y. La mienne ne se base pas sur les flots.

Algu-rythme, encore une fois, implémente l'algorithme ou bien donne-moi une preuve de correction de ce que tu avances car à première vue, ce n'est pas évident que ça marche. Par exemple, comment tu vas garantir que tu n'auras pas deux fois le même chemin ?

Si vous venez avec des solutions, ça serait sympa d'argumenter un peu sur la correction de votre solution. Il n'y a pas qu'une solution possible !

comment tu vas garantir que tu n'auras pas deux fois le même chemin ?

Par exemple, comment tu vas garantir que tu n'auras pas deux fois le même chemin ?

De la même façon que le dijkstra simple le garanti !

Dans la file à priorité on trouve plusieurs exemplaires du même nœud (un par arrête entrante déjà traitée), chacun avec une pondération distincte (technique du "tas paresseux", on autorise les doublons pour n'en depoper que k normalement, et on "jette" les autres qui sont périmés lorsqu'on les depop). En s'autorisant à traiter k fois un nœud chaque fois comme si c'était la première, on s'assure d'avoir les k premiers plus courts chemins vers ce nœud. On s'assure cependant de ne jamais faire de cycle, donc on ne repasse pas deux fois par le même nœud au cours d'un chemin, ainsi chaque nœud dans la file transporte trois informations : le nœud lui même, son poids, et une chaîne de bits (ou d'ID) nous informant des nœuds par lesquels passe déjà le chemin courant.

Je ne comprend pas bien ton algorithme. Si j'ai le graphe suivant :

L'algorithme devrait donner comme résultat :

$(2,3,\dots , k+1)$

Mais j'ai pas l'impression que c'est le cas si tu n'autorises pas les cycles. Mais encore une fois, c'est difficile de juger à première vue si ton intuition est bonne car tu donnes pas un algorithme très clair et il faut déchiffrer l'idée que tu as en tête.

Mais j'ai pas l'impression que c'est le cas si tu n'autorises pas les cycles.

En effet, en autorisant les cycles le résultat est ok, mais sinon, non. Je te donne l'algo demain !

Ok j'attend ça. Merci d'y avoir réfléchi en tout cas.

Je trouve le contexte un peu ridicule, mais la question est intéressante.

A part faire un algorithme classique qui recherche tous les chemins possibles et ensuite qui prend les k ayant les coûts totaux les plus faibles (basiquement, recherche en largeur ou en profondeur puis filtrage), j'ai une autre idée. Elle reste à vérifier et j'ai la flemme d'implémenter ça. Ce qui est sûr c'est que c'est sans doute créatif, mais probablement pas efficace.

1. ON recherche le chemin le plus court de façon classique
2. ON supprime une arête appartenant au chemin. Nommons les noeuds aux extrêmités de l'arête supprimée U et V.
3. On recherche le chemin le plus court entre U et V.
4. S'il n'exite plus de chemin, on remet l'arête en place. IL n'est plus nécessaire de considérer aucun chemin sans cette arête. ON recommence au point 2 avec une autre.
5. Si on trouve un autre chemin, on l'enregistre et on ajoute les arêtes rencontrées comme potentiellement supprimables lors d'une prochaîne itération.
6. On supprime une autre arête et on recommence au point 2 jusqu'à ce qu'on n'ait plus d'arête potentiellement supprimable

Je ne sais pas si c'est très clair.... c'est une sorte de backtracking sur les arêtes qu'on peut supprimer.

C'est probablement rigolo, mais je doute que ce soit réellement efficace. Mieux vaut rechercher l'ensemble des chemins possibles puis filtrer.

@QuentinC :

Le contexte est voulu pour que ce soit ridicule. C'est mon hommage personnel (et peut-être raté) à des concours d'algorithmique comme Google HashCode.

Pour ton algorithme, ça ne va pas marcher. Je pense que le dernier exemple que j'ai exhibé à Algue-Rythme fournit un contre-exemple pour ton algorithme aussi.

On peut généraliser Dijsktra facilement, j'avoue. Par contre, je me demande si on peut faire de même avec Bellman-Ford…