Bonjour à tous.
Dans ce défi je vous propose de réaliser une simulation de feu de forêt à travers un modèle simple (pour ne pas dire simpliste). Si vous vous fichez des histoires de percolation et que vous voulez simplement programmer, vous pouvez sauter la section suivante.
La percolation
La percolation désigne l’idée de passer au travers. L’exemple typique est celui du café. Pour faire du café (la boisson), il faut faire passer de l’eau dans du café (la graine) moulu. Une solution consiste à mettre le café dans un filtre et faire passer l’eau dedans ; en passant, elle va se charger en poudre de café. Si vous serrez le filtre plus fortement, l’eau mettra plus de temps pour traverser le café moulu, et la boisson finale sera plus forte. Cependant, si vous serrez trop, l’eau ne passera plus : la percolation n’a plus lieu.
On voit ici apparaître un seuil. En deçà, l’eau passe, au delà, non. L’existence d’un seuil est très général dans les cas de percolation. Si vous voulez en savoir plus sur la percolation, notamment du point de vue mathématique, je vous redirige vers l’article de Hugo Duminil-Copin.
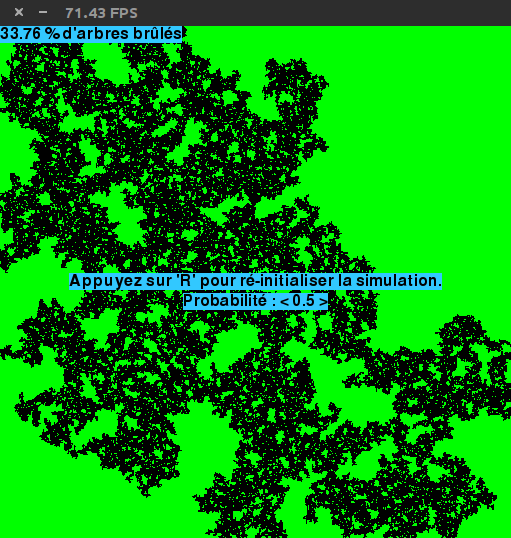
Dans le cas d’une simulation de feux de forêt, le seuil de percolation sera vue ainsi : si, partant d’un incendie originel, la forêt brûle presque entièrement, il y a percolation. Si seule une petite zone brûle, il n’y a pas percolation. Cette transition est très nette. Dans la cas d’une forêt pleine sur un réseau carrée, elle a lieu si la probabilité de propagation de l’incendie est de 0,5. Typiquement, sur un réseau 2D de 100x100, le nombre moyen d’arbre brûlé passe de moins de 100 (moins de 1%) à plus de 9000 (plus de 90%) quand cette probabilité passe de 0,4 à 0,6. Pour des compléments, ainsi que quelques résultats théorique, je vous renvoie vers un mémoire très propre sur le sujet.
La simulation
Pour commencer, on va considérer une grille. Chaque case de la grille pourra contenir soit des cendres, soit un arbre, soit un arbre en feu. Elles contiennent toute à la base un arbre.
On remplace le contenu de l’un des cases (choisie aléatoirement) par un arbre en feu.
La règle de propagation de l’incendie est la suivante : on considère une case en feu. Chacun de ses voisins, si c’est un arbre, à une probabilité p (déterminée à l’avance, c’est le paramètre de notre simulation) de devenir un arbre en feu. Une fois tous les voisins testés, la case considérée devient des cendres. On teste alors la case en feu suivante.
Le programme se termine quand plus aucune case n’est en feu. L’information utile est typiquement la proportion d’arbre ayant brûlé.

Attention à ce qui se passe aux bords ! Pour éviter les problèmes, le plus simple est de placer dans chacune des cases aux bords des cendre plutôt qu’un arbre (mais il ne faudra pas les compter dans le calcul de la proportion d’arbres brûlés).
Pour améliorer le modèle, on peut imaginer les situations suivantes :
- La bords sont constituée d’arbre, mais le bord gauche est accolé au bord droit, et le haut en bas. Autrement dit, on travaille sur un tore. En physique, on parle de condition aux bords périodiques ;
- La forêt est parsemée de trou : une partie des cases est constituée de terrain vague qui ne brûle pas. Prenez garde à la manière dont vous calculez la proportions d’arbre brûlé ;
- Le réseau est hexagonal au lieu de carré.
Vous pouvez aussi faire une sortie graphique, même si la proportion d’arbre ayant brûlé est suffisant pour ce défi.
Bien sûre, on voudrait théoriquement faire des statistiques sur nos simulations, donc s’assurer qu’elles sont efficaces. Si vous trouvez ce défi trop simple, n’hésitez pas à chercher à faire quelque chose d’efficace. Un système un peu grand (1000 par 1000) avec un p proche mais supérieur de 0,5 donne déjà une simulation assez lente.
Un défi plus corsé
Vous trouvez la simulation précédente trop facile ? Dans ce cas, je vous propose une autre simulation de percolation plus compliquée, en particulier dans l’analyse des résultats. Une version plus détaillé de ce problème a été présentée par GéoMl17, alias Micmaths, sur Openclassrooms.
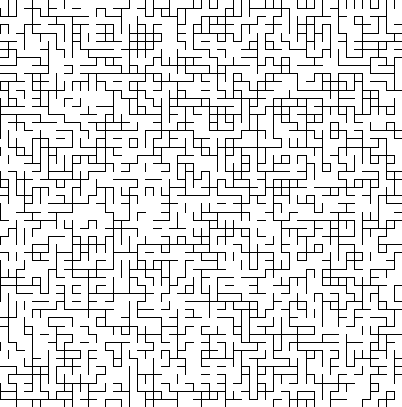
On considère un réseau de point régulièrement espacé, et on s’intéresse aux segments qui relient les points. Ils ont une probabilité p d’être plein, et 1-p d’être vides. On applique cela pour chaque segment. Si p est grand, on pourra passer de quasiment n’importe quel segment plein à n’importe quel autre. Si p est plus faible, on va avoir des domaines au sein desquels on peut se déplacer, mais qui ne sont pas liés entre eux. Le but est d’identifier les domaines en question.
Dans ce modèle, il y a percolation par exemple s’il est possible de passer de gauche à droite (ce qui est équivalent à dire que l’on ne peut pas passer de haut en bas en sautant de segments vides en segments vides)
Pour ce faire, vous pouvez vous inspirez de ce qui existent pour les recherches de chemin ou les parcours… d’arbre.
Sur ce, n’hésitez pas à montrer votre code, ou à poser des questions, que ce soit sur la percolation ou sur l’implémentation des simulations.
Les codes
Ici seront ajoutés les différents codes proposés, classés par langage.
Ada
C
fromvega, variante à 6 états (2 brulant, 2 ne brulant pas, le feu et les cendres). Images disponibles.
yoch, avec des détail sur le côté algorithmique.
C++
Berdes, en utilisant un automate cellulaire.
Olybri, jolie animation avec la SFML.
Raymo, parallélisation avec openMPI.
S-sonic`, affichage en temps réel avec la SFML.
C#
ThuleMalta, avec affichage.
Coffeescript
Excel
AurelB. Avec Excel… En VBA. Le code.
Fortran
Gabbro, tentative d’usage des forall sur un modèle avec des trous placés aléatoirement, et une probabilité de brûler fixée à 1 (inspiré par yoch).
Haskell
Javascript
luuka, avec une démo live.
Python
Aabu, avec un lac.
Folaefolc, modèle de base avec affichage.
Gabbro, modèle de base uniquement (code ayant servi a générer les premières images du défi).
klafyvel, avec affichage.
yoch, une variante avec des trous placés aléatoirement, et une probabilité de brûler fixée à 1.
Scheme
kelepoc, version épidémiologie.
Windev
elegence, avec des trous.







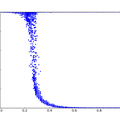






 ). C'est le résultat correspondant au fichier d'entrée forestfire_input2.txt, présent dans le dépôt github.
). C'est le résultat correspondant au fichier d'entrée forestfire_input2.txt, présent dans le dépôt github.