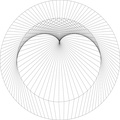
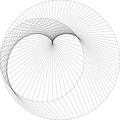
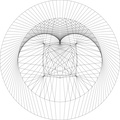
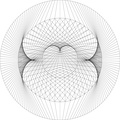
Quelques cas particuliers, abordés ou pas dans la vidéo de Micmaths. La plupart de ce qui suit correspond à des pensées furtives, non formalisées. Il est tout à fait possible que je rate une explication évidente, et je le poste plus comme une ouverture à la discussion que comme des explications. Ceci étant dit, voyant voir ces cas partiuliers.
Vous pouvez essayer par exemple 300 points avec un facteur de 149, qui va vous donner un quadrillage, ou avec un facteur de 199, qui va vous donner un maillage triangulaire. Pour comprendre ce qui ce passe, calculez $149^2 [300]$ et $199^2 [300]$. De la même manière, en prenant un facteur de 150, tous les points sont reliés uniquement à deux points sur le cercle, selon leur parité. Et en prenant 300, tous les points sont reliés à un point unique.
Vous pouvez aussi essayer avec des facteurs plus complexes, mais il est beaucoup plus dur de ce rendre compte de ce qui se passe, et c'est beaucoup moins plaisant esthétiquement. Par exemple, $107^4 [300]$ vaut 1, et puisque $107^2 [300]$ ne vaut pas 1 (mais 49), tous les traits d'un cercle à 300 points avec un facteur 107 font partie d'un motif à 4 cotés (ces cotés peuvent se croiser).
On pourrait donc raisonnablement ce demander si il existe un facteur tel qu'en partant d'un point, on n'y retourne que lorsqu'on est déjà passé par tous les autres points. En applicant le même raisonnement, il suffit de regarder les résultats de $X^{299} [300]$, pour voir si l'un d'entre eux vaut 1 (où X est le facteur, entre 2 et 300). La réponse, c'est que ça n'existe pas si l'on a 300 points sur le cercle.
Si vous avez écrit un script pour calculer ces modulos, vous vous êtes sûrement rendu compte que parfois, ils valaient 0, et ce quelle que soit la puissance entière strictement supérieure à 1 associée. Avec 300 points sur ce cercle, c'est le cas pour 30, 60, 90, 120, 150, 180, 210, 240, et 270. Que peut-on en déduire sur ce qui sera affiché ? Simplement que tous les points vont être reliés à un point qui sera lui même relié à… lui même. Et donc, on va avoir un certains nombres de points auxquels tous les autres seront reliés. Comment peut-on savoir combien de points agiront comme "aimants" ? Simplement en multipliant le facteur jusqu'à ce qu'il soit égal à 0, modulo le nombre de points du cercle. Pour 30, on va donc avoir 10 "aimants", "centres", ou peu importe. pour 60, on en aura plus que 5 (60, 120, 180, 240 et 0). Pour 90, on aura donc 90, 180, 270, 60, 150, 240, 30, 120, 210 et 0. Soit 10 centres. Comment peut-on trouver ce nombre directement, sans passer par cette phase de calcul qui pourrait se réveler fastidieuse ? Il faut remarquer que ce que l'on cherche, c'est un couple d'entier naturel (n,m) tels que $Facteur*n=Nb_{points}^{Cercle}*m$ avec n aussi petit que possible. Ça se simplifie un peu en $\frac{n}{m}=\frac{Nb_{points}^{Cercle}}{Facteur}$. En reprenant les valeurs précédentes, pour un facteur 30 avec 300 points, on trouve facilement 10. C'est tout aussi facile pour 60 avec 300 points. Par contre, en divisant 300 par 90, si on simplifie la fraction, on se retrouve avec $10/3$, ce qui donne 10 "centres".
C'est surtout pour le paragraphe directement au dessus que je disais que c'était simplement des pensées désordonnées. Il est surement possible de formaliser ça pour expliquer de manière claire et succinte ce qui se passe, mais là je vais aller dormir.