Bonjour,
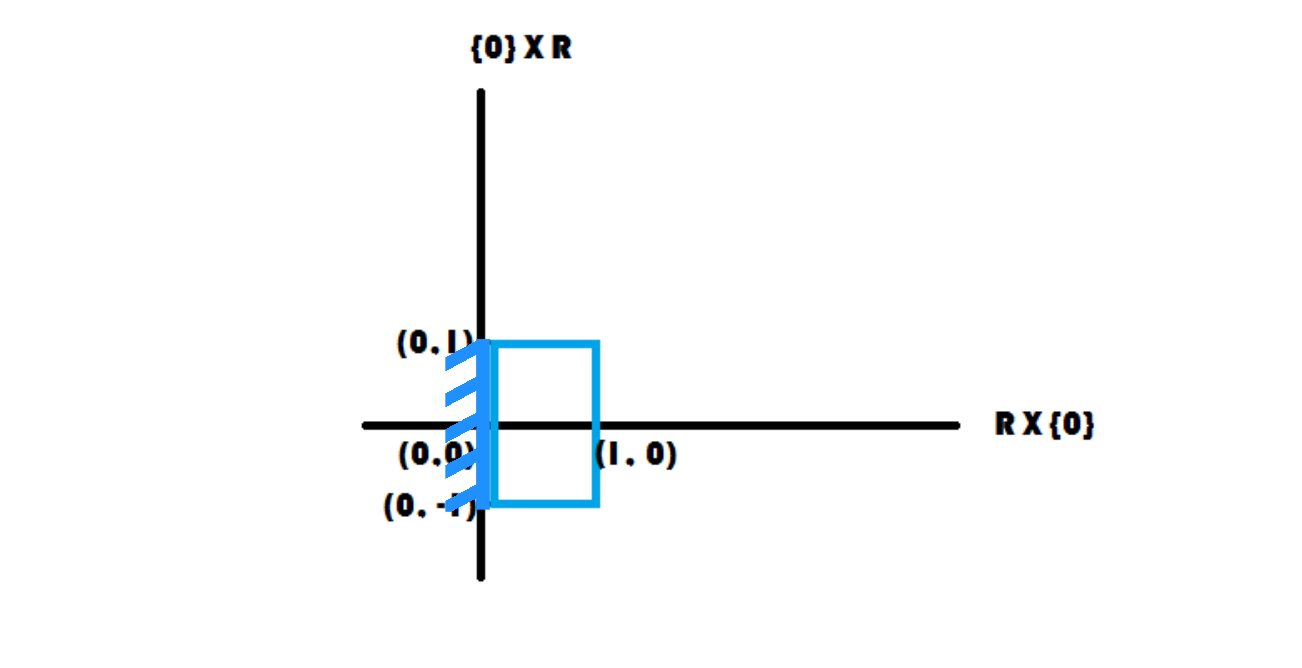
Je dois représenter $]0,1] \times [-1,1]$ dans $\mathbb R^2$.
Comment représenter l’exclusion du zéro alors? Faut-il simplement dessiner quelque chose comme ça :
Merci.
Non surtout pas.
Y a pas de convention générale à ma connaissance. Le mieux est décrire sur le côté la description de l’ensemble.
En revanche il ne faut pas décaler le trait, ce qui représente une tout autre configuration.
"Le mieux est décrire sur le côté la description de l’ensemble."
Et alors que dois-je dessiner?
Ça date pour moi, mais il n’y a pas une convention avec des hachures ?
Édit : trais sur l’axe 0, comme le signale Holosmos, je précise !
Ah oui, je n’y avais pas pensé.
Il est joli ton corbeau 2.0 Gabbro.
Bon je ne vais pas me prendre la tête pour ça, je met des hachures et pi voilà. 
Merci pour votre aide !
Les hachures ça fait pas très propre mais bon, pourquoi pas.
De toute façon, hachure ou pas, il faudra indiquer quelque part que c’est ouvert à gauche.
J’ai déjà vu dessiné en pointillés quand c’est exclu et en traits pleins quand c’est inclus (et c’est ce que je vois aussi quand je cherche sur internet).
Je dessinerais un rectangle avec un fond bleu clair, et des bordures bleu foncé, mais uniquement 3 bordures sur les 4. Mais comme ce n’est pas une convention connue/fréquente, il faut bien sûr expliquer la convention à côté.
Je dessinerais un rectangle avec un fond bleu clair, et des bordures bleu foncé, mais uniquement 3 bordures sur les 4. Mais comme ce n’est pas une convention connue/fréquente, il faut bien sûr expliquer la convention à côté.
C’est pas très cool pour les daltoniens ton affaire (il y a en a qui ont du mal avec les nuances claires/foncées). Pourquoi faire compliqué quand on peut faire simple comme les pointillés ?
Maintenant, on me demande de représenter $(\mathbb R - ]0, 1[ \cup [2, 3[) \times ((\mathbb R - [−1, 1]) \cap [0, 2])$, dois-je simplement faire apparaître les intervalles exclus?
À ma connaissance, il n’y a pas de convention universelle pour les dessins d’ensembles ; l’essentiel est qu’il soit le plus intelligible possible. Ici, pour moi la meilleure solution, pour des raisons de lisibilité, est de dessiner le complémentaire de ton ensemble (i.e. les intervalles exclus).
De toute manière, tu ne pourras pas échapper à quelques indications textuelles pour préciser.
Ajout — J’ai lu que certains suggèrent de hachurer les frontières lorsqu’un ensemble est ouvert. C’est à mon avis une très mauvaise idée, au sens où on pourrait tout à fait imaginer que les hachures indiquent que l’ensemble « continue ». C’est même assez courant d’adopter cette convention.
À ma connaissance, il n’y a pas de convention universelle pour les dessins d’ensembles
Il y en a une, elle utilise des symboles un peu étranges comme $\mathbb R$ ou $\cap$. Elle est vachement concise en plus. 
J’ai vraiment du mal à représenter $(\mathbb R - ]0, 1[ \cup [2, 3[) \times ((\mathbb R - [−1, 1]) \cap [0, 2])$… Vous avez pas un coup de pouce?
PS : Quel est l’intérêt de cet exercice mathématiquement parlant?
Vous avez pas un coup de pouce?
Tu peux déjà essayer de représenter chacun des deux ensembles sur chaque axe de ton domaine sans faire le produit pour l’instant.
PS : Quel est l’intérêt de cet exercice mathématiquement parlant?
Vérifier que tu as capté le sens des différents opérateurs, j’imagine.
Merci pour ton conseil qui m’a aidé.
Cependant, a-t-on : $(C_{\mathbb R} [−1, 1]) \cap [0, 2] = ]1, 2]$?
Eh bien $x \in (\mathbb R \cap [0,2]) \iff (x \in \mathbb R)$ et $(x \in [0,2])$.
Or, $[0,2] \subset \mathbb R$ donc si $x \in [0,2]$ alors $x \in \mathbb R$. De ce fait, $\mathbb R \cap [0,2] = [0,2]$.
En excluant $[-1, 1]$ de $\mathbb R$, on ne considère plus que $]1,2]$.
Après réflexion j’obtient quelque chose comme cela, où les pointillés représentes les exclusions :
Ça me semble correct.
Ok, donc j’ai pas grand chose à ajouter.
Bonne soirée, merci pour votre aide.
Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte
