Ce tuto a pour vocation de présenter les accords et renversements les plus utilisés, expliquant ainsi quelques bases de la théorie musicale classique. Nous verrons ainsi les accords parfaits et les septièmes de dominante.
Il est préférable de savoir lire les notes et d’avoir quelques bases en musique (intervalles, etc.) pour lire ce tuto.
Ce n’est en aucun cas une description exhaustive de tous les accords que l’on peut rencontrer, mais plutôt une présentation générale des plus fréquents.
- Rappels (ou pas)
- L'accord parfait à trois notes
- Les renversements de l'accord parfait
- Bilan intermédiaire
- Accords de septième
- Accord de septième de dominante
- Les renversements de l'accord de septième de dominante
- Récapitulatif des accords
- Mise en pratique
Rappels (ou pas)
Nous parlons ici de musique classique tonale.
Avant de rentrer dans le vif du sujet, je vais réexpliquer quelques notions qui seront très utiles pour la suite. Je suppose cependant que vous connaissez les notes, et que vous savez vous repérer sur une partition.
Les intervalles
Un intervalle entre deux notes désigne sa distance. En général, on résonne modulo l’octave (soit 12 demi-tons).
| Nombre de tons | Intervalle | Note par rapport à Do |
|---|---|---|
| 1/2 | Seconde mineure | Do |
| 1 | Seconde Majeure | Ré |
| 1+1/2 | Tierce mineure | Ré |
| 2 | Tierce Majeure/Quarte diminuée | Mi / Fa |
| 2+1/2 | Quarte juste | Fa |
| 3 | Quarte augmentée/Quinte diminuée | Fa / Sol |
| 3+1/2 | Quinte juste | Sol |
| 4 | Quinte augmentée/Sixte mineure | Sol /La |
| 4+1/2 | Sixte Majeure/Septième diminuée | La/Si |
| 5 | Septième Mineure | Si |
| 5+1/2 | Septième Majeure | Si |
| 6 | Octave | Do |
On remarque que certains intervalles ont plusieurs appellations : c’est selon l’utilisation qui en est faite.
Les degrés
Un degré désigne la place d’une note dans une échelle musicale. Ceux-ci sont notés en chiffres romains allant de I à VII.
| Degré | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|
| Nom | Tonique | Sus-tonique | Médiante | Sous-dominante | Dominante | Sus-dominante | Sensible |
| Exemple en Do Majeur | Do | Ré | Mi | Fa | Sol | La | Si |
| Exemple en La Majeur | La | Si | Do | Ré | Mi | Fa | Sol |
Les degrés ont des fonctions bien particulières, et on peut en particulier mentionner le fait que l’enchaînement V-I est conclusif, et on le retrouvera souvent à la fin d’une phrase musicale.
Les tonalités
Pour faire court, la tonalité est le ton définissant l’état stable d’un morceau. Elle peut être Majeure ou mineure.
Pour savoir en quelle tonalité on est, il suffit en général de regarder les dièses et bémols. Ensuite, on se rapporte à une figure comme celle-ci (source : wikipédia) :
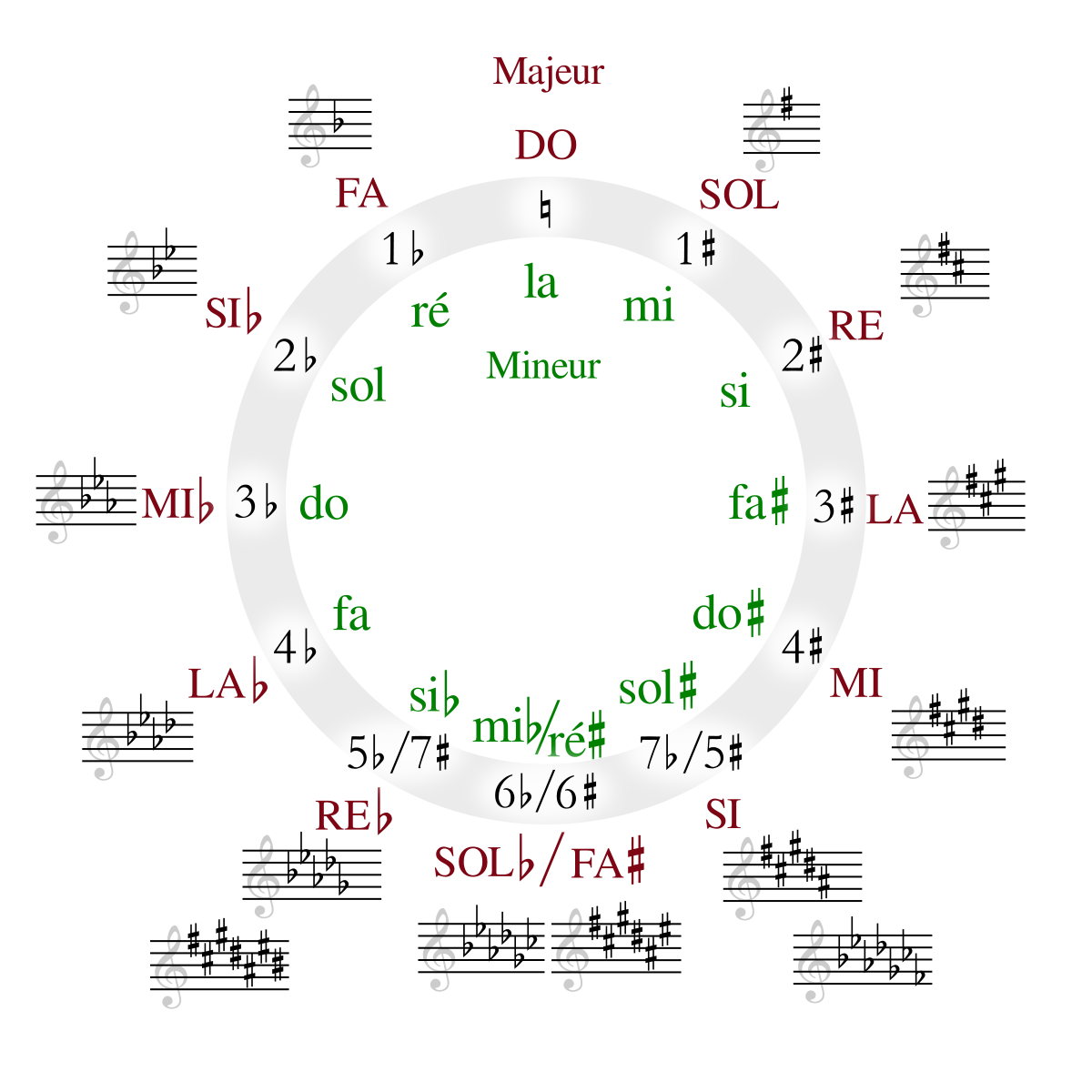
Pour vous aider à appréhender un peu mieux cette image, voici quelques clés de lecture :
- quand on fait le tour dans un sens ou dans un autre, on ajoute une quinte à chaque pas
- pour passer du Majeur au mineur (de l’extérieur à l’intérieur), on enlève une tierce mineure
- la tonalité est altérée (par exemple Fa m) s’il y a un dièse sur la tonique (en Fa m, le Fa est dièse).
L'accord parfait à trois notes
Un accord est un ensemble de notes, 3 ou plus. Les intervalles qui le composent vont lui donner sa couleur.
Un accord à trois notes est appelé « triad » dans la langue de Shakespeare et parfois « triade » en français, même si ce terme est plus facilement employé dans le jazz.
Commençons par l’accord le plus utilisé à trois notes. Sa forme théorique est formée par :
- la note fondamentale (ou juste la fondamentale) qui donnera son nom à l’accord
- au-dessus : une tierce (majeure ou mineure)
- Au-dessus de la tierce : la quinte. Si elle est juste, l’accord sera dit parfait

Si la tierce est majeure, on aura un accord majeur.
Si la tierce est mineure, on aura un accord mineur.
Si l’on regarde cet accord pour chaque degré, en se plaçant en Do Majeur, on obtient :

- les accords de Do, Fa et Sol sont des accords parfaits majeurs
- les accords de Ré, Mi, La sont des accords parfaits mineurs
- l’accord de Si a une tierce mineure, mais une quinte diminuée entre le Si et le Fa. Ce n’est donc pas un accord parfait, mais de quinte diminuée
En mineur harmonique, c’est légèrement différent : les degrés I et IV sont en mineur, les degrés V et VI en majeur, les II et VII de quinte diminuée et le III en quinte augmentée.
Il y a plusieurs formes du modes mineur : naturelle, harmonique et mélodique. On utilise souvent la forme harmonique, mais en notant explicitement les altérations qui ne font pas partie de la forme naturelle (le septième degré augmenté). Voir la page Wikipédia.
État fondamental
La note la plus grave est importante, car c’est la fondation de l’accord. Pour l’instant, nous avons considéré le cas où la note la plus grave correspondait au degré. Par exemple, dans un accord de Sol (Vème degré), il y avait un Sol à la basse.
Dans ce cas, on dit que l’accord est à l’état fondamental.
La fondamentale d’un accord désigne la note génératrice d’un accord. Par exemple, La pour La-Do-Mi.
Le fondamental ou l’état fondamental désigne la forme canonique d’un accord.
On chiffre cet accord ou , car l’intervalle entre la fondamentale et les autres notes sont une quinte (d’où le ) et une tierce (d’où le , que l’on omet souvent, car on le sous-entend).
Utilisation
L’état fondamental n’a pas d’utilisation particulière : c’est l’accord canonique. Par conséquent, on le rencontre fréquemment.
Redoublements
Dans la plupart des cas, la phrase musicale a plus de 3 voies. Dans ce cas, comme l’accord parfait ne possède que 3 notes distinctes, il faut en redoubler. Pour les accords parfaits en général, on va redoubler la fondamentale, éventuellement la quinte. On évitera de redoubler la tierce.
À l’état fondamental, on redoublera le plus souvent la basse.
Les renversements de l'accord parfait
L’état fondamental est le plus fréquent, mais il existe d’autres états. En effet, lorsque la basse est une autre note de l’accord, on dit que l’accord est renversé.
Pour un accord parfait, il y a deux cas :
- la tierce est à la basse : c’est le premier renversement
- la quinte est à la basse : c’est le deuxième renversement
Premier renversement
Le premier renversement est utilisé régulièrement. On l’appelle accord de sixte, et on le chiffre car l’intervalle entre la fondamentale et les autre notes sont une tierce et une sixte, mais on ne note pas la tierce (comme pour l’état fondamental).
Ce qui est important pour définir un accord de sixte, c’est que la basse soit la tierce. Après, l’ordre des autres notes est libre.
Redoublements
Tout comme pour l’état fondamental, on redoublera souvent la fondamentale, et plus rarement la quinte.
Exemples

Video : Exemples de l’état fondamental et du premier renversement
Quand on lit un accord, on va de bas en haut. Cela permet de commencer par la basse, qui définit l’état de l’accord.
Deuxième renversement
Le deuxième renversement est moins utilisé. On l’appelle accord de sixte et quarte, et on le chiffre . Pris seul, il sonne moins bien que les autres, à cause de la quarte que forme la basse avec la tonique. On l’utilisera donc avec plus de parcimonie. Il peut cependant être utilisé à des fins spécifiques (sixte et quarte de cadence par exemple).
Exemple
L’accord Mi-La-Do est un accord de La car il contient les bonnes notes : La, Do (la tierce) et Mi (la quinte). Comme la quinte (Mi) est à la basse, c’est un accord de sixte et quarte.
Conditions d’utilisation
Comme cet accord sonne plutôt mal tout seul, il y a certaines règles qu’il faut essayer de respecter quand on l’utilise, pour lisser le passage de l’accord et faire en sorte que ça sonne mieux :
- la préparation. Il faut avoir une des notes qui forment la quarte qui soit déjà présent dans l’accord précédent
- la résolution. Dans l’accord suivant un accord de sixte et quarte, il faut qu’une des deux notes de la quarte descende d’un ton, un demi-ton, ou reste identique
Préparation

Résolution

Les notes vertes sont les notes de préparation. Les rouges sont les notes de résolutions. Les liaisons sont ici simplement pour souligner les notes concernées.
Utilisation
Voici quelques cas (dans l’ordre de la vidéo) où l’on peut utiliser un accord de sixte et quarte :
- passage : pour passer d’un degré à un autre. Si la basse effectue un mouvement de trois notes consécutives ascendantes ou descendantes, alors l’accord du milieu peut être un accord de sixte et quarte
- broderie : la basse est immobile, et l’accord facilite un enchaînement, où est juste là pour faire joli
- cadence : l’accord vient préparer la dominante d’une cadence
Ici, les notes vertes sont les préparations, les notes rouges sont les résolutions et les bleues sont les accords de sixte et quarte.
Vous l’avez peut-être remarqué, le dernier accord est considéré comme V alors que c’est un accord de I. C’est un cas particulier de notation : un accord de de cadence s’écrit presque toujours V chiffré , car il sonne plus comme un V avec une double appogiature que comme un I.
Redoublements
Tout d’habitude, on redoublera souvent la fondamentale. Cependant, comme la basse est la quinte, on pourra aussi facilement redoubler la quinte.
Récapitulatif
Récapitulatif des trois états possibles pour un accord majeur (Do) et un accord mineur (Mi), ainsi que quelques formes possibles à voix. Notez les répétitions de la basse ou de la quinte.

Bilan intermédiaire
Avec ce que l’on a appris, nous en savons déjà suffisamment pour identifier certains accords dans un morceau.
Petit exercice : identifier les degrés et déterminer les états dans le petit morceau ci-dessous.
Attention : nous sommes en La mineur, ce qui signifie que le premier degré est La et non plus Do comme auparavant.
Réponse :

Rappelez-vous que le I chiffré de cadence s’écrit V chiffré , car il sonne plus comme un V avec une double appogiature que comme un I.
Pour donner un ordre d’idée en termes de fréquence d’apparition des degrés, on voit très souvent le I et le V, un peu moins les IV et II, de temps en temps un VI, rarement un III, et jamais le VII.
Finalement, ce n’est pas si difficile, et avec quelques ces quelques bases on peut déjà construire une phrase musicale. Passons maintenant à d’autres accords, toujours très utilisés.
Accords de septième
Nous passons maintenant au niveau supérieur, avec des accords à 4 notes. Bien entendu, nous n’avons pas étudié tous les accords à 3 notes, mais une liste exhaustive serait longue est peu intéressante.
Intéressons-nous donc aux accords de septième. Ils se construisent de façon simple : une fondamentale, une tierce, une quinte, et une septième.
En fait, c’est comme l’accord parfait, mais auquel on ajoute encore une septième.
Avec 3 notes, on a déjà plusieurs possibilités : la tierce peut être Majeure ou mineure, la quinte peut être juste (accord parfait), diminuée ou augmentée.
Avec 4, on ajoute à toutes ces possibilités la septième, qui peut être Majeure, mineure, et même parfois diminuée.
Exemples :
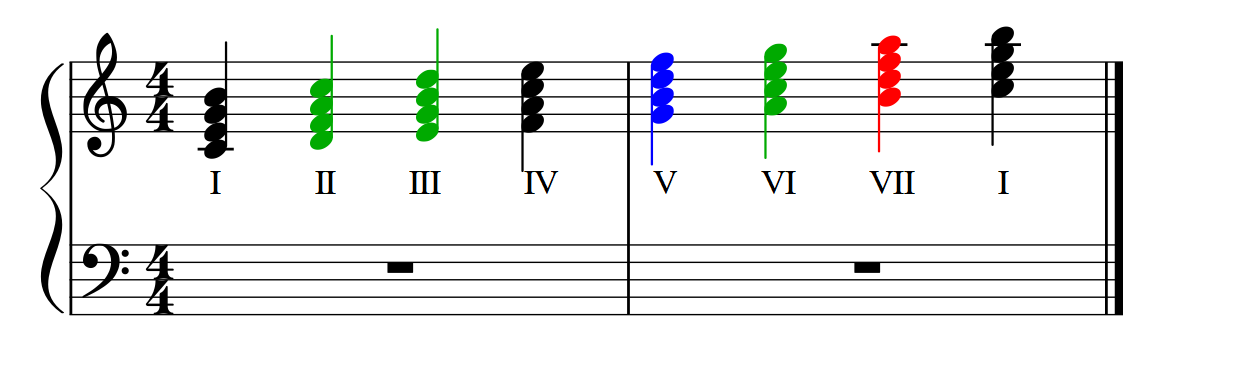
- les accords des degrés I et IV sont des accords avec tierce Majeure et tierce mineure
- les accords des degrés II, III et VI ont une tierce mineure et une septième mineure
- l’accord du degré VII a une tierce Majeure, une quinte diminuée et une septième mineure
- l’accord du degré V a une tierce Majeure et une septième mineure
Tous les accords de septième ne sont pas présents. Par exemple, l’accord de septième diminuée, couramment utilisé, n’existe qu’en mineur (en La, ce sera l’accord Sol-Si-Ré-Fa).
Nous allons nous intéresser particulièrement à l’accord de septième de dominante (accord de septième sur le degré V), car il est largement utilisé.
Les autres accords de septième s’appellent des accords de septièmes d’espèces. On peut en rencontrer dans divers contextes, comme ici  .
.
Accord de septième de dominante
L’accord de septième de dominante est un accord à 4 notes très utilisé. On l’entend souvent lors des cadences (à la fin d’une phrase musicale).
La septième de dominante, comme son nom l’indique, est sur la dominante. Ainsi, il s’utilise comme l’accord à trois sons du V, mais possède en plus la dissonance engendrée par la septième.
La construction est sans ambiguïté, et il est constitué de :
- une tierce majeure
- une quinte juste
- une septième mineure
Contrairement à l’accord parfait vu auparavant, cet accord est identique en majeur et mineur.
La résolution
Règle à bien retenir : la septième d’un accord de septième de dominante se résout en descendant sur la tierce.
État fondamental
L’état fondamental se construit en empilant les intervalles énoncés en partant d’une note choisie. Par exemple, si je choisis la fondamentale comme étant Si, alors l’accord final sera :
- un Ré : la tierce majeure de Si
- un Fa : la quinte juste de Si
- un La : la septième mineure de Si
Comme c’est un accord de septième de dominante et que la fondamentale est Si, nous sommes en Mi (Majeur ou mineur).

La septième de dominante doit avoir une tierce Majeure. Pour cette raison on met un dièse sur le Ré.
Chiffrage
On chiffre cet accord .
Là, pour le chiffrage c’est un peu subtil. Le indique la sensible, donc comme cet accord est composé d’une septième, d’une quinte et d’une tierce à la sensible, il devrait être chiffré , mais pour que ce soit plus lisible, on omet les tierces et quintes dans les chiffrages, donc le disparaît et le devient , d’où le .
Utilisation
On peut utiliser cet accord presque partout où l’on utilise une dominante. Seulement, il implique une dissonance donc ce n’est pas judicieux d’en mettre partout. De plus, cet accord a besoin d’être résolu donc cela implique des restrictions sur l’accord suivant.
Les renversements de l'accord de septième de dominante
Tout comme l’accord parfait, l’accord de septième de dominante possède des renversements. Cependant, comme cet accord a 4 notes et pas 3, il possède 4 états.
Il est intéressant de bien comprendre et de retenir ces accords, car ils sont très souvent utilisés.
Premier renversement
Le premier renversement s’obtient quand on a la tierce à la basse.
Par exemple, en Do Majeur, l’accord de septième de dominante est composé des notes Sol-Si-Ré-Fa. La tierce de Sol est Si, donc dans le premier renversement c’est Si qui sera à la basse.

On peut remarquer que le dernier accord ne possède pas de Ré.
C’est normal : les notes indispensables d’un accord de septième de dominante sont la fondamentale, la septième, et la tierce. On peut donc omettre la quinte. Cependant, si on oublie la quinte, il faut redoubler une note. On essaye tout comme pour les accords parfaits de redoubler la fondamentale ou la quinte (on ne redouble pas la septième). Ici la quinte est absente donc on redouble la fondamentale.
Chiffrage
On peut appeler cet accord accord de quinte diminuée et sixte.
Cet accord est chiffré (six, cinq barré). Le six correspond à l’intervalle entre la basse et la fondamentale et le cinq barré correspond à la quinte diminuée entre la basse et la septième. La tierce quant à elle, est omise dans le chiffrage.
Utilisation
L’accord de septième de dominante est intéressant, certes, mais ce serait une grosse erreur de ne l’utiliser que sous forme fondamentale. En effet, celle-là est lourde et son utilisation serait maladroite au cours et non pas à la fin d’une phrase musicale.
Le premier renversement, plus léger, pourra être utilisé avantageusement en cours de phrase.
De plus, cela permet à la basse d’être plus chantante, car l’enchaînement V-I5 ou V-I6 utilisera plutôt des notes conjointes que des grands intervalles (de quinte par exemple).
Deuxième renversement
Le deuxième renversement s’obtient lorsque c’est la quinte qui est à la basse.
Petit exemple, en Ré Majeur pour changer.

Cet accord va se comporter comme une sixte et quarte de passage. En effet, cet accord sonne moins bien que les autres états de la septième de dominante. On fera donc attention, tout comme pour l’accord de sixte et quarte de passage, à avoir un mouvement de basse conjointe. Il n’est cependant pas nécessaire de préparer la quarte.
Le premier exemple est cependant un peu spécial : comme la résolution se fait au I6, mais que la septième doit descendre à la tierce, alors la tierce se retrouve doublée. Si elle est à l’unisson, comme ici, il n’y a pas de problème. Mais s’il y a bien deux tierces, elle est quand même acceptée mais seulement si elle est au ténor. C’est un peu capillotracté, mais bon, ce n’est pas moi qui ait inventé les règles et les exceptions qui vont avec.
Chiffrage
On peut appeler cet accord accord de sixte sensible.
Cet accord se chiffre , en référence à la sixte entre la basse et la sensible ( fait référence à la sensible).
Utilisation
Comme dit précédemment, cet accord est très peu utilisé. On l’utilisera un peu comme une sixte et quarte de passage.
Troisième renversement
Le troisième renversement se forme, vous l’aurez deviné, en mettant la septième à la basse. Cela a pour effet d’intensifier la dissonance.
Exemple en Mi mineur (pour changer un peu)

Ce renversement doit nécessairement aboutir à un accord ayant le troisième degré comme basse. En effet, la septième doit descendre à la tierce. Ainsi, cet accord a une moins grande valeur conclusive que les autres, car l’enchaînement V-I implique obligatoirement un I6.
De plus, on aura souvent (mais pas obligatoirement) la sensible au soprano.
Chiffrage
Comme l’intervalle entre la fondamentale et la sensible est une quarte, on chiffrera cet accord ( faisant référence à la sensible).
On pourra appeler cet accord accord de triton, en référence à la quarte augmentée (également appelée triton).
Utilisation
On peut utiliser cet accord librement, donc de la même manière que l’état fondamental et que le premier renversement. Il ne sera cependant pas utilisé lors de cadences conclusives, à cause du I6 obligatoire.
Récapitulatif des accords
Petit tableau récapitulatif des accords que nous avons rencontrés.
| Nom | Chiffrage | Exemple en Do Majeur | Remarques |
|---|---|---|---|
| Accord parfait à l’état fondamental | 5 |  |
Très utilisé |
| Accord de sixte | 6 |  |
Couramment utilisé |
| Accord de sixte et quarte |  |
Attention à la préparation et à la résolution | |
| Septième de dominante à l’état fondamental |  |
Couramment utilisé | |
| Accord de quinte diminuée et sixte |  |
Couramment utilisé | |
| Accord de sixte sensible |  |
Utilisation restreinte | |
| Accord de triton |  |
Moins conclusif que les autres renversements |
Mise en pratique
Maintenant que vous connaissez les accords les plus connus, on va essayer de les retrouver dans un vrai morceau.
Je ne vais pas vous donner de la musique qui passe à la radio parce que j’ai envie que vous écriviez plus de deux accords. Bon ok, j’exagère, parfois, il y en a 3. Voire 4 (comme pour le légendaire La m-Fa-Do-Sol).
Premier exercice
On va commencer par un morceau à trous. Je vais vous donner quelques mesures avec des accords déjà remplis, et vous allez compléter. C’est extrait d’un petit morceau de Bach : la cantate « Jesus bleibet meine Freude » BWV 147 (on peut avoir une version orchestrale ici).
Petite remarque : le septième degré n’existe pas vraiment. S’il y a des notes du septième degré, alors c’est probablement un accord de sixte sur la dominante, ou quelque chose comme ça. En fait, les degrés que l’on rencontre sont dans l’immense majorité des cas I, V, IV, II et VI.
Si vous voulez juste l’image :

Et la correction qui va avec :

L’accord de V de V peut sembler un peu obscur, mais c’est juste un accord de septième de dominante sur le V. On le repère grâce au Do .
Deuxième exercice
Un peu plus compliqué cette fois. Voici le début d’une sonate en Fa Majeur de Haydn (Joseph de son prénom) qui a vécu au XVIIᵉ siècle. Mis à part le premier accord de la 5ᵉ mesure (Do-Fa-Si), et la 10ᵉ mesure (avec le Mi b) vous avez toutes les clés en main pour trouver les accords de ce début de morceau.
Attention, je n’ai jamais dit que c’était facile. Il faut tout d’abord déterminer quelles sont les notes qui composent accords (notes réelles), et quelles notes sont étrangères (elles sont là pour la déco).
Voilà donc le bout à analyser :

Il ne faut pas hésiter à aller l’écouter, donc par exemple ici histoire de bien voir de quoi il s’agit. En plus, ça aide pour l’analyse. Petite remarque : les chiffres qui sont déjà là sont les doigtés (histoire d’aider un peu l’interprète qui devra jouer ça).
Bon, sans plus attendre, voici la solution :

Remarque : l’avant-dernier accord est un peu spécial. On considère qu’il y a une appogiature, et c’est le plus simple, car on a pas besoin de le chiffrer.
Les accords avec des points d’interrogations sont un peu plus compliqués. Ce sont des accords de V de IV. En gros, ce sont des accords de septième de dominante pour le quatrième degré (donc des accords de Fa Majeur avec une septième mineure, d’où le Mi ).
Comme vous avez pu le constater sur ces deux exemples, on rencontre en effet beaucoup les degrés I et V, et on voit beaucoup d’accords à l’état fondamental (surtout ici pour les accords de septièmes).
Comme vous avez pu le constater, la musique n’est pas faite au hasard. Il y a toute une théorie qui vise non pas à embêter le musicien, mais à l’aider à faire les choses proprement pour que ce soit plus joli. J’espère en tout cas que ce tuto vous encouragera à avoir un œil (ou plutôt une oreille) critique sur la musique de manière générale.
Merci pour tous ceux qui m’ont encouragé et notamment nohar pour sa relecture pendant la bêta et qwerty pour la prise en charge de la validation.




 ), ça s’est révélé plus dur (au point que je tirais quelquefois au sort les accords, jugeant selon la probabilité d’occurrence).
), ça s’est révélé plus dur (au point que je tirais quelquefois au sort les accords, jugeant selon la probabilité d’occurrence). . Mis à part ça, la mesure 11 me questionne : un accord de II équivaudrait Sol-Si-Ré en Fa majeur, non ? Or, il y a un Mi. Du coup, je ne comprends pas mon erreur à ce niveau.
. Mis à part ça, la mesure 11 me questionne : un accord de II équivaudrait Sol-Si-Ré en Fa majeur, non ? Or, il y a un Mi. Du coup, je ne comprends pas mon erreur à ce niveau. !
!


