Dessiner la fractale de Mandelbrot

Dessiner la fractale de Mandelbrot

Ce tutoriel a pour but de vous faire découvrir l’univers des fractales en informatique et plus particulièrement celui de l’ensemble de Mandelbrot.

Attention, ce tutoriel requiert une certaine base de connaissance en mathématiques. Même si je vais expliquer le plus dur, il est nécessaire d’avoir une solide connaissance de l’arithmétique de base : +,−,×,x2,x+,-,\times,x^2,\sqrt{x}.

Tout d’abord, qu’est-ce qu’une fractale (ou figure fractale) ? Je ne vais pas vous donner la vraie définition qui est tout à fait incompréhensible pour la plupart des personnes. En fait, une fractale est une figure complexe qui possède une infinité de détails, quelle que soit l’échelle à laquelle on la regarde. De plus on retrouve souvent le même motif ou un motif similaire dans le motif de la fractale en lui-même. Pour finir, il faut dire qu’une fractale est trop irrégulière pour que l’on puisse la décrire par des termes géométriques habituels.

Voici quelques exemples de fractales :

Ensemble de julia Éponge de Menger Ensemble de Mandelbrot

Vous avez sans doute déjà vu la dernière. C’est l’ensemble de Mandelbrot, la fractale sur laquelle nous allons travailler.

Préliminaires

Les nombres complexes

Afin de comprendre la formule qui définit l’ensemble de Mandelbrot, il faut tout d’abord savoir ce qu’est un nombre complexe.

Un nombre complexe est un nombre qui possède deux parties : une partie réelle et une partie imaginaire. La partie réelle est un nombre quelconque appartenant à l’ensemble des réels. La partie imaginaire est aussi un nombre appartenant à l’ensemble des réels.

C’est quoi cette arnaque ? Pourquoi on a un nombre composé de deux nombres ?

Et bien, le nombre complexe aura pour valeur sa partie réelle additionné à sa partie imaginaire, elle-même multipliée par ii. Si on note xx la partie réelle et yy la partie imaginaire, le nombre complexe, noté zz, sera z=x+iyz=x+iy. Notez au passage l’utilisation de xx et yy, habituellement utilisés pour les coordonnés d’un point. La plus grosse difficulté des nombres complexes vient du fait qu’il est courant de définir ii par i2=−1i^2=-1.

Mais, je croyais qu’un nombre au carré était toujours positif ? o_O

C’est vrai pour tous les réels (les nombres que l’on étudie le plus souvent), mais ce n’est pas forcément vrai pour les nombres complexes, à cause de cette propriété particulière que possède ii. Il faudra vous y faire. Un exemple de nombre complexe : 3+5i3+5i. 33 est la partie réelle et 55 la partie imaginaire.

Voici quelques exemples d’opérations sur les nombres complexes pour que vous compreniez.

  • L’addition : (17+3i)+(4+6i)=(17+4)+(3+6)i=21+9i(17+3i)+(4+6i)=(17+4)+(3+6)i=21+9i. Comme vous pouvez le voir, il suffit d’additionner les parties réelles et les parties imaginaires entre elles pour obtenir le résultat.
  • La multiplication : (17+3i)×(4+6i)(17+3i)\times (4+6i). D’abord, on développe : 17×4+17×6i+3i×4+3i×6i17\times 4+17\times 6i+3i\times 4+3i\times 6i. Ensuite, on rassemble les éléments et on simplifie : 68+114i+18i268+114i+18i^2. Et là, miracle : i2=−1i^2=-1, donc on peut continuer à simplifier : 68+114i−18=50+114i68+114i-18=50+114i.

Les nombres complexes peuvent être utilisés pour représenter un point dans un repère. Par exemple, le point de coordonnées (2;4)(2;4) peut être représenté par le nombre complexe 2+4i2+4i. On voit que la partie réelle du nombre complexe correspond à l’abscisse du point et la partie imaginaire à l’ordonnée. Dans le cas général, le nombre complexe z=x+iyz=x+iy correspond au point M de coordonnées (x;y)(x;y). On dit que zz est l’affixe de M. En continuant là-dessus, il faut savoir que la distance OMOM correspond au module du nombre zz. On peut donc en déduire que le module de zz, noté ∣z∣|z|, est égal à x2+y2\sqrt{x^2+y^2}. Retenez bien cette notion, c’est important pour la suite.

C’était la partie la plus dure, donc si vous avez compris tout ça, le reste devrait rester assez simple.

Je précise aussi que ce n’est qu’une petite introduction aux nombres complexes et que je n’ai abordé que les points nécessaires à la compréhension de la suite du tutoriel.

Les suites

Le second point de math qu’il faut connaitre est les suites.

En mathématiques, une suite est une famille d’éléments indexée par les entiers naturels.

Wikipédia

La définition de Wikipédia est plus ou moins claire, mais le plus important est la partie en gras. Par exemple, si on parle de la suite (Un)(U_n), le nom de la suite est UU et l’index est nn.

Une suite peut être définie directement en fonction de nn. C’est le cas le plus simple, en voici un exemple : Un=5n+1U_n=5n+1. C’est un peu comme une fonction, sauf que nn est forcément un entier positif : U3=5×3+1=16U_3=5\times 3+1=16.

Mais il existe une autre méthode pour définir une suite : on définit le premier terme de la suite et une formule de récurrence qui va nous permettre de calculer un terme en fonction du précédent. Un exemple : le premier terme U0=1U_0=1 et la formule de récurrence Un+1=3Un−1U_{n+1}=3U_n-1. Pour calculer U2U_2, on va procéder comme ceci :

U2=3U1−1=3(3U0−1)−1=3(3−1)−1=6−1=5\begin{aligned} U_2 &= 3U_1-1 \\ &= 3(3U_0-1)-1 \\ &= 3(3-1)-1 \\ &= 6-1 \\ &= 5 \end{aligned}

Rien de bien compliqué au final si on a déjà compris le principe des fonctions.

Si vous êtes arrivés ici vivants et que vous avez compris l’essentiel, la suite de ce tutoriel devrait vous sembler très simple.

L'ensemble de Mandelbrot

Ses caractéristiques

L’exemple de l’ensemble de Mandelbrot donné dans l’introduction peut être trompeur, car il y a plein de couleurs, mais en réalité la fractale n’est qu’une figure. Sur l’image ci-dessous, on voit clairement la fractale en noir.

Mandelbrot en noir et blanc

La grosse forme qui ressemble presque à un cercle est appelée cardioïde (vous avez une petite explication sur Wikipédia). Comme vous pouvez le voir, le cercle à gauche de la cardioïde est lui-même entouré de cercles de différentes tailles et cela se répète tout au long de la fractale de manière infinie. Une autre caractéristique, c’est les petits points qui sont à gauche de la fractale. Normalement, ils forment un segment qui s’arrête brusquement (vous pouvez le voir sur la fractale en couleur). Et bien, si on zoome sur ce segment on retrouvera toujours la fractale et ce quel que soit le zoom que l’on prend.

La formule

En se servant des connaissances que vous avez acquises juste avant, vous pouvez enfin comprendre la formule qui définit l’ensemble de Mandelbrot.

L’ensemble de Mandelbrot est une fractale qui est définie comme l’ensemble des points cc du plan complexe pour lesquels la suite récurrente définie par Zn+1=Zn2+cZ_{n+1}=Z^2_n+c et la condition Z0=0Z_0=0 ne tend pas vers l’infini (en module).

Wikipédia

Pour faire plus simple, on regarde chaque point du plan complexe (de l’image) et on regarde si la suite tend vers l’infini en module (c’est à dire si le module de ZnZ_n pour nn très grand se rapproche de l’infini). En réalité, ce genre de calcul est bien compliqué pour notre pauvre ordinateur et donc, nous avons seulement besoin de tester si le module de ZnZ_n dépasse 22 à un moment. S’il ne le dépasse pas, c’est qu’il fait partie de la fractale.

Mais comment savoir s’il ne le dépasse pas?

On va tout simplement vérifier qu’il ne dépasse pas 2 jusqu’à un certain rang assez grand pour que l’on puisse raisonnablement penser qu’il ne le dépassera pas ensuite. C’est le rang (appelé nombre d’itérations) que l’on va choisir qui va fixer en partie la qualité du rendu final. Si le nombre d’itérations n’est pas assez grand, on va considérer trop de points comme faisant partie de la fractale, alors que si le nombre d’itération est trop grand, la fractale aura tendance à être trop nette (c’est un peu le problème de la fractale en noir et blanc que je vous aie montrée juste au-dessus).

L'algorithme

Bon, maintenant que vous savez comment définir la fractale de Mandelbrot, on va passer à la pratique : on va créer l’algorithme qui va nous permettre de dessiner la fractale. Pourquoi un algorithme plutôt qu’un code ? Tout simplement car on peut dessiner l’ensemble de Mandelbrot avec quasiment tous les langages, donc pour que tout le monde puisse le traduire, on va définir une méthode qui doit marcher quel que soit le langage que l’on utilise. Ce sera ensuite à vous de le traduire dans votre langage favori.

Le premier jet est assez simple :

définir iteration_max = 50

Pour chaque point de coordonnées (x; y) du plan :
    définir c = x + iy
    définir z = 0
    définir i = 0

    Faire
        z = z*z + c
        i = i+1
    Tant que module de z < 2 et i < iteration_max

    si i = iteration_max
        dessiner le pixel correspondant au point de coordonnées (x; y)
    finSi
finPour

Notez que le i dans ce code correspond au nombre d’itérations et non pas au nombre imaginaire ii.

Comme vous pouvez le voir, ce code est très simple, mais sera difficilement traduisible si on utilise un langage qui ne comprend pas les nombres complexes. C’est pour cela que l’on va définir 2 variables pour le nombre zz : une pour la partie réelle zrz_r et une pour la partie imaginaire ziz_i. On va faire de même pour cc. Le calcul z=z×z+cz=z\times z+c devient donc :

z=z2+c=(zr+izi)2+(cr+ici)=zr2+2izrzi+(izi)2+cr+ici=zr2+2izrzi−zi2+cr+ici=(zr2−zi2+cr)+i(2zrzi+ci)\begin{aligned} z &= z^2+c \\ &= (z_r+iz_i)^2+(c_r+ic_i) \\ &= z_r^2+2iz_rz_i+(iz_i)^2+c_r+ic_i \\ &= z_r^2+2iz_rz_i-z_i^2+c_r+ic_i \\ &= (z_r^2-z_i^2+c_r)+i(2z_rz_i+c_i) \end{aligned}

Il ne reste plus qu’à séparer la partie entière et la partie imaginaire :

zr=zr2−zi2+crzi=2zrzi+ci\begin{aligned} z_r &= z_r^2-z_i^2+c_r\\ z_i &= 2z_rz_i+c_i \end{aligned}

Attention, il ne s’agit pas d’égalités mathématiques, mais de la décomposition du calcul de zz dans le code.

De plus, au lieu de calculer le module de zz et le comparer à 2, on va juste calculer le carré de ses composantes (partie réelle et partie imaginaire) et comparer le résultat à 4 car : zr2+zi2<2⟺zr2+zi2<4\sqrt{z_r^2+z_i^2}<2 \Longleftrightarrow z_r^2+z_i^2<4

On peut donc changer le code comme ceci :

définir iteration_max = 50

Pour chaque point de coordonnées (x; y) du plan :
    définir c_r = x;
    définir c_i = y;
    définir z_r = 0
    définir z_i = 0
    définir i = 0

    Faire
        définir tmp = z_r
        z_r = z_r*z_r - z_i*z_i + c_r
        z_i = 2*z_i*tmp + c_i
        i = i+1
    Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

    si i = iteration_max
        dessiner le pixel correspondant au point de coordonnées (x; y)
    finSi
finPour

On stocke zrz_r dans une variable temporaire pour éviter d’utiliser la nouvelle valeur de zrz_r dans le calcul de ziz_i.

Rien ne vous choque ? Et bien ça devrait. En informatique, on va utiliser une image pour dessiner la fractale, sauf que là on utilise un plan pour les coordonnées de xx et yy. Il va donc falloir faire correspondre ces deux grandeurs. Tout d’abord, il faut savoir que l’ensemble de Mandelbrot est toujours compris entre -2.1 et 0.6 sur l’axe des abscisse et entre -1.2 et 1.2 sur l’axe des ordonnées.

Il y a deux techniques pour gérer la différence de taille entre le plan et l’image utilisée.

La plus simple consiste à définir la zone que l’on va dessiner et une valeur de zoom. On calculera ensuite la taille de l’image à partir de ces informations :

// on définit la zone que l'on dessine. Ici, la fractale en entière
définir x1 = -2.1
définir x2 = 0.6
définir y1 = -1.2
définir y2 = 1.2
définir zoom = 100 // pour une distance de 1 sur le plan, on a 100 pixels sur l'image
définir iteration_max = 50

// on calcule la taille de l'image :
définir image_x = (x2 - x1) * zoom
définir image_y = (y2 - y1) * zoom

Pour x = 0 tant que x < image_x par pas de 1 
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = x / zoom + x1
        définir c_i = y / zoom + y1
        définir z_r = 0
        définir z_i = 0
        définir i = 0

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i = iteration_max
            dessiner le pixel de coordonnées (x; y)
        finSi
    finPour
finPour

Avec ce code, on obtiendra une image de 270*240 pixels. Les avantages de cette technique :

  • on définit soit-même l’échelle (le zoom) que l’on veut ;
  • la fractale a toujours les mêmes proportions.

L’inconvénient : on ne connait pas la taille finale de l’image sans la calculer soi-même avant. Il y a donc des risques de se retrouver avec une image bien trop grande (et l’ordi va patauger pour dessiner la fractale) ou une image bien trop petite.

La deuxième technique est tout simplement de définir la zone que l’on veut dessiner et la taille de l’image. Le zoom sera calculé en fonction de ces valeurs :

// on définit la zone que l'on dessine. Ici, la fractale en entière
définir x1 = -2.1
définir x2 = 0.6
définir y1 = -1.2
définir y2 = 1.2
définir image_x = 270
définir image_y = 240
définir iteration_max = 50

// on calcule la taille de l'image :
définir zoom_x = image_x/(x2 - x1)
définir zoom_y = image_y/(y2 - y1)

Pour x = 0 tant que x < image_x par pas de 1
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = x / zoom_x + x1
        définir c_i = y / zoom_y + y1
        définir z_r = 0
        définir z_i = 0
        définir i = 0

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i = iteration_max
            dessiner le pixel de coordonnées (x; y)
        finSi
    finPour
finPour

L’avantage : on a une image de la taille que l’on veut, donc il n’y a pas de risque de se retrouver avec une image de 10000*10000.

L’inconvénient : à moins de calculer soi-même la taille de l’image en fonction de la taille de la zone à dessiner (et là, ça reviendrait à la première technique), on se retrouve souvent avec une image complètement disproportionnée.

Voilà pourquoi je préfère utiliser la première technique, quitte à avoir une validation qui demande si on veut vraiment dessiner la fractale en indiquant la taille de l’image.

À partir de ce stade, vous pouvez déjà faire un rendu de la fractale. Voici ce que j’ai fait en recopiant le code :

Premier rendu de Mandelbrot

Le chiffre en haut à gauche, c’est le temps de génération en secondes. C’est un peu long, mais en grosse partie à cause de PHP qui n’est pas vraiment adapté. D’après mon expérience, en utilisant un langage bas niveau tel que C ou C++, on peut arriver très facilement à des résultats 10 à 20 fois plus rapides. Et en utilisant des outils spécialisés (qui se servent de la carte graphique), vous pourrez avoir des rendus de la taille de votre écran à 60 fps. :)

D’ailleurs, en parlant du PHP, voici le code que j’ai utilisé pour générer la fractale :

<?php
$x1 = -2.1;
$x2 = 0.6;
$y1 = -1.2;
$y2 = 1.2;
$zoom = 100;
$iterations_max = 50;

$image_x = ($x2 - $x1)*$zoom;
$image_y = ($y2 - $y1)*$zoom;

// on crée l'image et les couleurs, inutile ici de remplir l'image vu qu'on dessinera tous les pixels
$image = imagecreatetruecolor($image_x, $image_y);
$blanc = imagecolorallocate($image, 255, 255, 255);
$noir  = imagecolorallocate($image, 0, 0, 0);
imagefill($image, 0 ,0 , $blanc);

$debut = microtime(true);
for($x = 0; $x < $image_x; $x++){
    for($y = 0; $y < $image_y; $y++){
        $c_r = $x/$zoom+$x1;
        $c_i = $y/$zoom+$y1;
        $z_r = 0;
        $z_i = 0;
        $i   = 0;

        do{
            $tmp = $z_r;
            $z_r = $z_r*$z_r - $z_i*$z_i + $c_r;
            $z_i = 2*$tmp*$z_i + $c_i;
            $i++;
        } while($z_r*$z_r + $z_i*$z_i < 4 AND $i < $iterations_max);

        if($i == $iterations_max)
            imagesetpixel($image, $x, $y, $noir);
    }
}

$temps = round(microtime(true) - $debut, 3);

imagestring($image, 3, 1, 1, $temps, $noir);

header('Content-type: image/png');
imagepng($image);

En couleur, c'est plus joli

Nous y voilà enfin, dans la partie qui vous permettra de faire de super beaux rendus qui feront craquer tout le monde (ou pas). L’intégration de la couleur dans la fractale se fait de manière très simple : vous avez remarqué que quand on sort de la boucle qui teste si ZnZ_n tend vers l’infini en module, on ne dessine rien ? Et bien il suffit de dessiner le pixel avec une couleur en fonction du nombre d’itération que l’on a mis pour trouver que ZnZ_n tend vers l’infini en module.

On va prendre l’exemple simple de la fractale entourée de bleu. Donc plus on met d’itération, plus le bleu est clair.

définir x1 = -2.1
définir x2 = 0.6
définir y1 = -1.2
définir y2 = 1.2
définir zoom = 100 // pour une distance de 1 sur le plan, on a 100 pixels sur l'image
définir iteration_max = 50

définir image_x = (x2 - x1) * zoom
définir image_y = (y2 - y1) * zoom

Pour x = 0 tant que x < image_x par pas de 1 
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = x / zoom + x1
        définir c_i = y / zoom + y1
        définir z_r = 0
        définir z_i = 0
        définir i = 0

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i = iteration_max
            dessiner en noir le pixel de coordonné (x; x)
        sinon
            dessiner avec couleur rgb(0, 0, i*255/iteration_max) le pixel de coordonnées (x; x)
        finSi
    finPour
finPour

Voici le rendu (mêmes paramètres que pour le précédent) :

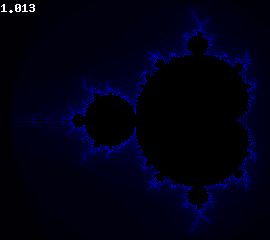
Mandelbrot avec un peu de couleur

C’est loin d’être très beau, mais la base est là. Sachez que pour trouver les bons paramètres et les bonnes couleurs, il vous faudra beaucoup de tests souvent infructueux. Pensez tout de même que souvent les plus belles fractales ont des dégradés de plusieurs couleurs. Ici, on ne va que du noir vers le bleu. Mais on peut très bien aller du noir vers le bleu, puis vers le blanc. On peut même faire un cycle de couleur : noir -> bleu -> blanc -> vert -> noir et on recommence.

Si vous regardez bien pour le premier ensemble de Mandelbrot que je vous aie montré (dans l’introduction), le créateur a utilisé le dégradé bleu foncé -> blanc -> jaune -> violet -> bleu -> blanc. Vous n’êtes pas non plus obligé d’utiliser un dégradé linéaire, à vous de laisser parler votre imagination.

Voici le code PHP de la fractale en couleur :

<?php
$x1 = -2.1;
$x2 = 0.6;
$y1 = -1.2;
$y2 = 1.2;
$zoom = 100;
$iterations_max = 50;

$image_x = ($x2 - $x1)*$zoom;
$image_y = ($y2 - $y1)*$zoom;

// on crée l'image et les couleurs, inutile ici de remplir l'image vu qu'on dessinera tous les pixels
$image = imagecreatetruecolor($image_x, $image_y);
$blanc = imagecolorallocate($image, 255, 255, 255);
$noir  = imagecolorallocate($image, 0, 0, 0);
imagefill($image, 0 ,0 , $blanc);

// on définit la liste des couleurs du dégradé ici, ça évite de devoir faire appel à imagecoloralocate à chaque pixel
$couleurs = array();
for($i = 0; $i < $iterations_max; $i++)
    $couleur[$i] = imagecolorallocate($image, 0, 0, $i*255/$iterations_max);

$debut = microtime(true);
for($x = 0; $x < $image_x; $x++){
    for($y = 0; $y < $image_y; $y++){
        $c_r = $x/$zoom+$x1;
        $c_i = $y/$zoom+$y1;
        $z_r = 0;
        $z_i = 0;
        $i   = 0;

        do{
            $tmp = $z_r;
            $z_r = $z_r*$z_r - $z_i*$z_i + $c_r;
            $z_i = 2*$tmp*$z_i + $c_i;
            $i++;
        } while($z_r*$z_r + $z_i*$z_i < 4 AND $i < $iterations_max);

        if($i == $iterations_max)
            imagesetpixel($image, $x, $y, $noir);
        else
            imagesetpixel($image, $x, $y, $couleur[$i]);
    }
}

$temps = round(microtime(true) - $debut, 3);

imagestring($image, 3, 1, 1, $temps, $blanc);

header('Content-type: image/png');
imagepng($image);

Finalement, pour ceux qui ont besoin de plus de performances, voici le code en C++ avec SFML (merci à Gigotdarnaud de m’avoir fourni le code) :

#include <iostream>
#include <SFML/Graphics.hpp>

sf::Mutex mutex;
bool threadRun;

class Render : public sf::Thread
{
    // Cette classe threadée va s'occuper des calculs, afin de ne pas bloquer l'affichage
    public:

    Render(sf::Image** _im, unsigned int _zoom, unsigned int _max_iteration, bool _inColor=false)
    {
        *_im=&im; //On utilise un pointeur de pointeur afin que le thread principal puisse afficher l'image

        inColor=_inColor;

        x1=-2.1;
        x2=0.6;
        y1=-1.2;
        y2=1.2;
        zoom=_zoom;
        iteration_max=_max_iteration;

        image_x = static_cast<unsigned int>((x2 - x1) * zoom);
        image_y = static_cast<unsigned int>((y2 - y1) * zoom);

        std::cout << "Image size : (" << image_x << ";" << image_y << ")" << std::endl;

        im=sf::Image(image_x, image_y, sf::Color::Black); //On crée une image vide (noire)
        threadRun=true; //Cette variable globale sert à stopper le thread lorsque l'on ferme la fenêtre.
    }

    private:

    virtual void Run() //La fonction principale du thread de rendu
    {
        for(unsigned int x=0;x<image_x&&threadRun;x++) //On parcourt l'axe des X
        {
            for(unsigned int y=0;y<image_y&&threadRun;y++) //On parcourt l'axe des Y
            {
                double c_r=x/static_cast<double>(zoom)+x1;
                double c_i=y/static_cast<double>(zoom)+y1;
                double z_r=0;
                double z_i=0;
                double i=0;

                do
                {
                    double tmp=z_r;
                    z_r=z_r*z_r-z_i*z_i+c_r;
                    z_i=2*z_i*tmp+c_i;
                    ++i;
                }
                while(z_r*z_r+z_i*z_i<4&&i<iteration_max&&threadRun);

                if(threadRun)
                {
                    mutex.Lock(); //On verrouille l'image, afin que les deux threads n'entrent pas en collision
                    if(inColor)
                    {
                        if(i!=iteration_max)
                        {
                            im.SetPixel(x, y, sf::Color(0, 0, static_cast<int>(i*255/iteration_max))); //On change la couleur du pixel
                        }
                    }
                    else
                    {
                        if(i==iteration_max)
                            im.SetPixel(x, y, sf::Color::White);
                    }
                    mutex.Unlock(); //Et on dévérouille
                }
            }
        }
        if(threadRun)
        {
            //Si l'on est arrivé ici, c'est que l'on a calculé tout ce qui était calculable.
            std::cout << "Render is over (" << elapsed.GetElapsedTime() << "s) ! Saving..."<<std::endl;
            im.SaveToFile("Fractal.png");
            std::cout << "Saved in \"Fractal.png\""<<std::endl;
        }
        else
        {
            //Si on est là, c'est que le rendu a été stoppé prématurément par l'utilisateur.
            std::cout << "Rendering aborded."<<std::endl;
        }
    }

    double x1;
    double x2;
    double y1;
    double y2;
    unsigned int zoom;
    unsigned int iteration_max;

    unsigned int image_x;
    unsigned int image_y;

    sf::Clock elapsed; //Cet objet servira à déterminer le temps de rendu à postériori

    bool inColor;

    sf::Image im;
};

int main()
{
    //On crée la fenêtre, on prépare le sprite et l'image...
    const unsigned int RESO_X=800;
    const unsigned int RESO_Y=600;
    sf::RenderWindow App(sf::VideoMode(RESO_X, RESO_Y, 32), "Fractales");
    App.SetFramerateLimit(60);

    sf::Image* ima=NULL;

    Render rend(&ima, 2500, 500, true); //On créé l'objet du rendu, en lui donnant les paramètres de la fractale (zoom, itérations max et couleur)

    sf::Sprite spr;
    spr.SetImage(*ima);

    //Cet objet sert à limiter l'appel aux fonctions d'affichage, qui bloquent le thread de rendu à cause des mutexs.
    sf::Clock clock;
    const float time = 0.25;

    //Cet objet sert à déterminer le zoom de la vue, la position de la caméra, etc. Elle n'a qu'une influence sur la fenêtre, la fractale est toujours la même
    sf::View view(sf::Vector2f(ima->GetWidth()/2,ima->GetHeight()/2), sf::Vector2f(RESO_X/2,RESO_Y/2));
    App.SetView(view);

    //On lance le thread de rendu
    rend.Launch();

    while(App.IsOpened())
    {
        sf::Event Event;
        while (App.GetEvent(Event)) //On parcourt la pile des évènements
        {
            if (Event.Type==sf::Event::Closed)
            {
                App.Close();
            }
            else if(Event.Type==sf::Event::MouseWheelMoved) //Zoom/Dézoom à la molette de souris
            {
                if(Event.MouseWheel.Delta>0)
                {
                    view.Zoom(1.5);
                }
                else
                {
                    view.Zoom(0.75f);
                }
            }
            else if(Event.Type==sf::Event::KeyPressed) //Déplacement
            {
                if(Event.Key.Code == sf::Key::Left)
                {
                    view.Move(-10,0);
                }
                else if(Event.Key.Code == sf::Key::Right)
                {
                    view.Move(10,0);
                }
                else if(Event.Key.Code == sf::Key::Up)
                {
                    view.Move(0,-10);
                }
                else if(Event.Key.Code == sf::Key::Down)
                {
                    view.Move(0,10);
                }
            }
        }

        if(clock.GetElapsedTime()>time) //Si suffisamment de temps s'est écoulé depuis le dernier affichage
        {
            clock.Reset();
            mutex.Lock(); //On verrouille l'image
            App.Draw(spr); //On l'affiche
            App.Display(); //On rafraichit l'écran
            mutex.Unlock(); //On rend la main au thread de rendu
        }
    }

    threadRun=false; //Avant de quitter, il faut penser à stopper le thread de rendu.

    return 0;
}

Faire des zooms sur l'image

Étant donné que la question m’a été posée à plusieurs reprises, je vais vous expliquer comment faire pour zoomer sur l’ensemble de Mandelbrot.

Globalement, il n’y a pas de technique particulière pour obtenir un zoom sur une zone de la fractale, il s’agit juste de changer certains paramètres. Le tout, c’est de savoir lesquels changer et de quelle manière.

Le zoom

Le premier paramètre que l’on aurait tendance à changer si on veut zoomer, c’est le zoom (logique ^^ ). Donc oui, il faut l’augmenter. Mais si on n’augmente que le zoom, on va se retrouver avec une image d’autant plus grande (et donc plus longue à calculer) qu’on aura augmenté le zoom, et ce n’est pas forcément ce que l’on veut.

Les coordonnées du plan complexe

Les quatre premiers paramètres que l’on définit sont les coordonnées de la zone que l’on veut tracer. Voici à quoi ils correspondent :

  • x1 correspond à la limite gauche de l’image ;
  • x2 correspond à la limite droite de l’image ;
  • y1 correspond à la limite du haut de l’image ;
  • y2 correspond à la limite du bas de l’image.

Par exemple, si on augmente x1, l’image sera plus petite vers la droite. En diminuant x2, l’image sera petite vers la gauche. Et de même pour y1 et y2.

Le nombre d’itérations maximum

Enfin, le nombre d’itérations maximum est aussi important à faire augmenter quand on zoom beaucoup, car plus on zoom, plus il faut être précis.

Pour illustrer ce que l’on a vu au dessus, si je vous demande une image du quart en haut à droite de la fractale de la même taille que les autres images, il faudra : doubler le zoom, augmenter x1, diminuer y2 et un peu augmenter le nombre maximum d’itérations. On obtient donc :

  • zoom = 200
  • x1 = -0.75
  • y2 = 0
  • iteration_max = 100

Et voici le résultat :

Mandelbrot après zoom

De même si vous voulez zoomer sur un point du plan complexe de coordonnées (x;y)(x;y) en particulier, il faudra juste définir x1 = x-h, x2 = x+h, y1 = y-h et y2 = y+h. Avec h une valeur que vous fixerez vous-même en sachant que plus elle est petite, plus vous zoomerez sur ce point en particulier. Bien évidement, il faudra augmenter en conséquence le zoom et le nombre d’itérations.

Pour aller plus loin

Maintenant que vous avez les bases pour créer la fractale de Mandelbrot, dites-vous qu’il y a un bon nombre de fractales qui sont basées sur le même principe.

Les ensembles de Julia

Les ensembles de Julia sont basés sur le même principe que l’ensemble de Mandelbrot. La formule est exactement la même (Zn+1=Zn2+cZ_{n+1}=Z_n^2+c), seul les valeurs de départ changent : cc sera un nombre complexe fixe de votre choix (essayer de le prendre dans le plan complexe de l’ensemble de Mandelbrot) et Z0=x+iyZ_0=x+iy. La première fractale montrée dans le tutoriel est un ensemble de Julia. Sachez que si cc est situé dans la fractale de Mandelbrot, alors l’ensemble de Julia sera connexe, c’est-à-dire que la fractale sera d’un bloc. Alors que si cc n’est pas dans la fractale de Mandelbrot, l’ensemble de Julia sera formé de points non connectés.

Voici l’algorithme :

définir x1 = -1
définir x2 = 1
définir y1 = -1.2
définir y2 = 1.2
définir zoom = 100
définir iteration_max = 150

définir image_x = (x2 - x1) * zoom
définir image_y = (y2 - y1) * zoom

Pour x = 0 tant que x < image_x par pas de 1 
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = 0.285
        définir c_i = 0.01
        définir z_r = x / zoom + x1
        définir z_i = y / zoom + y1
        définir i = 0

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i = iteration_max
            dessiner le pixel de coordonnées (x; y)
        finSi
    finPour
finPour

C’est les valeurs de crc_r et cic_i qui vont déterminer la forme de l’ensemble. Avec les valeurs que j’ai mises dans l’algorithme, vous devriez obtenir la même forme que l’ensemble de Julia présenté dans l’introduction. Notez aussi que les ensembles de Julia sont centrés sur l’origine du repère, donc il faut modifier les coordonnés de x1, x2, y1 et y2 en conséquence. Si vous prenez (-1.5; 1.5) pour x et y, vous devriez toujours avoir l’ensemble en entier.

Vous pouvez aussi rajouter des couleurs de la même manière que pour l’ensemble de Mandelbrot. Voilà ce que j’obtiens avec exactement le même dégradé que pour l’ensemble de Mandelbrot :

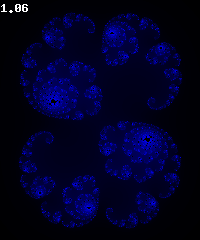
Un ensemble de Julia

Buddhabrot

Voilà une fractale qui a vraiment fait parler d’elle. En effet, elle ressemble beaucoup à un bouddha en train de méditer. Si vous voulez des exemples sur internet, vous pouvez en trouver beaucoup. La méthode de génération est proche de celle de la fractale de Mandelbrot, à la différence près qu’au lieu de dessiner les points appartenant à l’ensemble de Mandelbrot, on va dessiner le chemin pris par la suite avant quelle diverge (que son module ne dépasse pas 2). Dans ce tutoriel, on parcourra tous les points de l’image, mais en théorie on devrais prendre les points au hasard sur le plan complexe. Un petit code pour que vous compreniez mieux :

définir x1 = -2.1
définir x2 = 0.6
définir y1 = -1.2
définir y2 = 1.2
définir zoom = 100
définir iteration_max = 100

définir image_x = (x2 - x1) * zoom
définir image_y = (y2 - y1) * zoom

// un tableau que l'on va incrémenter à chaque fois que la suite Z_n passera par un point.
définir pixels comme un tableau 2D de image_x cases sur image_y cases avec toutes les cases initialisées à 0

// en théorie, on devrait faire une seul boucle dans laquelle on devrait prendre les coordonnées (x; y) au hasard.
Pour x = 0 tant que x < image_x par pas de 1
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = x / zoom + x1
        définir c_i = y / zoom + y1
        définir z_r = 0
        définir z_i = 0
        définir i = 0
        définir tmp_pixels comme une liste de coordonnées

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
            ajouter les coordonnées ((z_r-x1)*zoom; (z_i-y1)*zoom) au tableau tmp_pixels
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i != iteration_max
            Pour chaque valeurs pixel de tmp_pixels
                si la case pixels[pixel[0]][pixel[1]] existe
                    on incrémente la case en question
                finSi
            finPour
        finSi
    finPour
finPour

Pour chaque case de coordonnée (x; y) de l'image
    Dessiner le pixel de coordonnée (x; y) avec la couleur rgb(min(pixels[x][y], 255), min(pixels[x][y], 255), min(pixels[x][y], 255))
finPour

Avec ce code, plus la suite (Zn)(Z_n) passe par un point, plus il sera clair. Voici le résultat que j’obtiens (après quelques modifications des paramètres et une rotation de 90° vers la droite) :

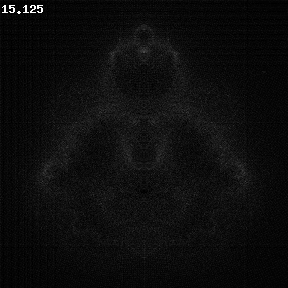
Le Buddhabrot

Comme vous pouvez le voir, c’est beaucoup plus long que pour la génération de la fractale de Mandelbrot, mais c’est en partie due à une augmentation de la taille et du nombre d’itérations.

Pour avoir des couleurs, la plupart du temps, on crée un tableau par partie de la couleur (rouge, vert et bleu) et on change le nombre d’itérations maximal pour chaque tableau. Il faut de grandes différences entre les itérations max pour avoir réellement de la couleur. Comme je sens que vous n’avez pas tout compris, je vous donne l’algorithme :

définir x1 = -2.1
définir x2 = 0.6
définir y1 = -1.2
définir y2 = 1.2
définir zoom = 100
définir iteration_rouge = 100
définir iteration_vert = 1000
définir iteration_bleu = 10000
définir iteration_max = max(iteration_rouge, iteration_vert, iteration_bleu)

définir image_x = (x2 - x1) * zoom
définir image_y = (y2 - y1) * zoom

définir pixels_rouge comme un tableau 2D de image_x cases sur image_y cases avec toutes les cases initialisées à 0
définir pixels_vert comme un tableau 2D de image_x cases sur image_y cases avec toutes les cases initialisées à 0
définir pixels_bleu comme un tableau 2D de image_x cases sur image_y cases avec toutes les cases initialisées à 0

// en théorie, on devrait faire une seul boucle dans laquelle on devrait prendre les coordonnées (x; y) au hasard.
Pour x = 0 tant que x < image_x par pas de 1
    Pour y = 0 tant que y < image_y par pas de 1
        définir c_r = x / zoom + x1
        définir c_i = y / zoom + y1
        définir z_r = 0
        définir z_i = 0
        définir i = 0
        définir tmp_pixels comme une liste de coordonnées

        Faire
            définir tmp = z_r
            z_r = z_r*z_r - z_i*z_i + c_r
            z_i = 2*z_i*tmp + c_i
            i = i+1
            ajouter les coordonnées ((z_r-x1)*zoom; (z_i-y1)*zoom) au tableau tmp_pixels
        Tant que z_r*z_r + z_i*z_i < 4 et i < iteration_max

        si i < iteration_rouge
            Pour les iteration_rouge premières valeurs pixel de tmp_pixels
                si la case pixels_rouge[pixel[0]][pixel[1]] existe
                    on incrémente la case en question
                finSi
            finPour
        finSi
        si i < iteration_vert
            Pour les iteration_vert premières valeurs pixel de tmp_pixels
                si la case pixels_vert[pixel[0]][pixel[1]] existe
                    on incrémente la case en question
                finSi
            finPour
        finSi
        si i < iteration_bleu
            Pour les iteration_bleu premières valeurs pixel de tmp_pixels
                si la case pixels_bleu[pixel[0]][pixel[1]] existe
                    on incrémente la case en question
                finSi
            finPour
        finSi
    finPour
finPour

Pour chaque pixel de coordonnées (x; y) de l'image
    Dessiner le pixel de coordonnées (x; y) avec la couleur rgb(min(pixels_rouge[x][y], 255), min(pixels_vert[x][y], 255), min(pixels_bleu[x][y], 255))
finPour

Voilà, c’est quand même un brin plus compliqué que pour la fractale de Mandelbrot. ^^ Ne soyez donc pas étonné de ne pas comprendre ça du premier coup, sachant que j’ai moi-même mis pas mal de temps à comprendre comment il fallait faire. Et il n’y a pas d’image cette fois-ci car je n’ai pas réussi à avoir un truc correct à vous présenter, si vous voulez trouvez des images, faite la recherche "buddhabrot" sur Google image, vous aurez plein d’images.

Mandelblub

Le Mandelblub est un essai de transformation de la fractale de Mandelbrot en 3D. Étant donné que cela dépasse largement mes compétences, je vais vous laisser 2 liens qui permettront aux plus gourmands d’entre vous de satisfaire leur appétit. Le premier est un article en anglais sur le Mandelblub, il présente de très nombreuses images de cette fractale, vous pourrez donc apprécier la page sans connaitre un mot d’anglais : http://www.skytopia.com/project/fractal/mandelbulb.html . Le deuxième est un article en français qui explique en détail la définition du Mandelblub et qui donne même une technique de rendu 3D pour les fractales : http://images.math.cnrs.fr/Mandelbulb.html .

Nous voici à la fin du tutoriel. Vous devriez être maintenant capable de dessiner des fractales en connaissant leur formule.

Si vous n’avez pas compris un point ou qu’il vous semble obscur, merci de me le signaler afin que ce tutoriel soit le plus accessible possible.

22 commentaires

Ce tutoriel qui plaira sans doute à Holosmos !

baptisteguil

Me semble avoir vu la même chose sur le feu SdZ, non ?

En tout cas je connais déjà le sujet, c'est toujours agréable de lire quelque chose qui rejoint ça même si ça n'est "que" une simulation. Les questions soulevées derrières sont à mon sens plus intéressantes que de jolies formes.

Cependant je suis pas ultra satisfait par le style d'écriture : pleins de conventions (pourquoi cette borne?) et des erreurs du genre "plan complexe" au lieu de "droite complexe".

+1 -1

et des erreurs du genre "plan complexe" au lieu de "droite complexe"

Ceci n'est pas une erreur. L'appellation plan complexe désigne un plan de $\mathbb R^2$ (qui est certes une droite de $\mathbb C$) où chaque point est la représentation d'un nombre complexe.

+0 -0

T'es d'accord pour dire "Droite complexe" en parlant de $\mathbf{C}$ ?

Tu trouves pas ça illogique de parler de droite ET de plan complexes pour le même objet ?

Au pire on s'en fout, ce sont juste des mots. Ce qui me gêne au fond c'est que je sais pas qui et comment cet article scientifique a été relu.

+1 -0

$\mathbb C$ est une droite, oui. Mais $\mathbb R^2$ est un plan. Le plan complexe tel que considéré dans le cadre de ce tuto et d'un tas d'autres écrits est $\mathbb R^2$ auquel on lie les éléments de $\mathbb C$. C'est pas illogique du tout, c'est juste une question de terminologie.

+2 -2

"Plan complexe" dit qu'un élément de ce plan a des composantes complexes. Or un élément du plan s'écrit en deux coordonnées : deux coordonnées complexes donc.

Pour moi y a une erreur, ce que tu dis là (et wiki aussi …) c'est le plan euclidien des nombres complexes. Un plan complexe n'est pas un plan euclidien … Je trouve ça illogique.

M'enfin supposons que j'ai tort. On en arrive à la conclusion que $\mathbf{C}$ est une droite et un plan complexes. Rien de simple.

Raison de plus à ma cause : on parle de plan projectif complexe et de droite projective complexe pour les dimensions $2$ et $1$ respectivement. Si y a une terminologie logique elle devrait s'appliquer ici aussi.

M'enfin quand même, disons que j'ai tort et que j'ai vraiment tort.

Le terme "fractal(e)" est ici utilisé abusément : aucune définition (d'ailleurs y en a pas une seule sur ce sujet, donc je suis étonné que l'auteur dise avoir la définition mais qui est trop complexe). On confond l'ensemble de Mandelbrot avec son caractère "fractal".

+1 -0

Oui, il y a le même tuto sur le SdZ (mais plus pour longtemps) puisque c'est de là qu'il vient.

Concernant les abus de langage et les fautes de vocabulaire, il me semble que j'avais écrit ce tuto quand j'étais encore en première, donc j'étais loin de maîtriser assez le sujet pour éviter ce genre de problème. Depuis, je n'ai pas fait de grosse modifications à ce niveau, surtout parce que l'on ne m'a jamais fait ce genre de remarques. Pour le terme "fractal(e)", je pourrais faire des corrections, tout en gardant à l'esprit que ce tuto n'a pas vocation à être une référence mathématique en la matière, mais plus une introduction à la représentation de la fractale de Mandelbrot. D'autant que le niveau requis pour comprendre ce genre de subtilité est largement supérieur au niveau requis pour le lire. Du coup, les lecteurs qui ont un bon niveau verrons qu'il s'agit d'inexactitudes ou d'abus et ça ne changera a priori rien pour les autres

Autrement, l'usage de "plan complexe" était courant (peut-être à tord) quand j'ai étudié ça, d'où le fait que je l'ai utilisé dans le tutoriel. Après, j'aurais tendance à être du même avis que @dri1 en disant que $\mathbb{C}$ et $\mathbb{R}^2$ sont isomorphes, que l'on manipule dans ce contexte plus les nombres complexes comme des éléments à 2 composantes (réelles) que l'on place sur un plan que comme des éléments à une composante (complexe) que l'on place sur une droite. Donc l'utilisation du mot "plan" me semble justifiée. Après, "plan complexe" désigne bel et bien le plan sur lequel on positionne des nombres complexes. Il s'agit peut-être d'un abus de langage, mais il est fortement utilisé, donc ça ne me semble pas utile (voir même contre-productif) de l'éliminer.

+0 -0

Vu que je ne suis pas qu'un emmerdeur absolu, voilà deux petites vidéos que je vous laisse regarder. L'idée est de déformer un ensemble de Mandelbrot en changeant le point "caractéristique" qui est originellement $0$ en un autre. Ça donne lieu à ce que vous pouvez voir.

C'est une petite partie de l'ensemble qui a été filmée, si je voulais tout prendre ça serait très lourd à exécuter mais si vous insistez je peux essayer.

Premier lien

Second lien (plus intéressant?)

+0 -0

Je conseillerais une coloration moins régulière, la plupart des points partent soit très vite soit très tard. Voilà une petite formule que j'avais faite pour mes simulations et qui rend bien :

1
int col = 255 - ((range>50) ? (50+(int)(0.5 + range*1.0/borne*205) ):range*2);

Avec "range" le nombre d'itérations nécessaires à la sortie. La valeur "col" me donne le niveau de gris nécessaire (je colore du blanc au noir).

+0 -0

Coucou,

Dans un autre registre, je trouve la présentation faite sur les nombres complexes particulièrement bancale et obscure. Si on se met à la place de quelqu'un qui n'y connait rien, il n'est pas près de comprendre quoi que ce soit.

Un nombre complexe est un nombre qui possède deux parties : une partie réelle et une partie imaginaire. La partie réelle est un nombre quelconque appartenant à l'ensemble des réels. La partie imaginaire est aussi un nombre appartenant à l'ensemble des réels.

Dommage que la notion de dimension ne soit ici jamais mentionnée. On n'explique pas ce qu'on entend par "partie" ni la notion de couple qui se cache derrière (alors que c'est la meilleure manière d'arriver au plan).

Et bien, le nombre complexe aura pour valeur sa partie réelle additionné à sa partie imaginaire, elle-même multipliée par $i$.

Heu, c'est quoi $i$ pondu par magie ?

Si on note x la partie réelle et y la partie imaginaire, le nombre complexe, noté z, sera z=x+iy.

Il aurait certainement été plus judicieux de partir de cela comme définition et d'expliquer à partir de là ce que sont les parties imaginaire et réelle plutôt que… l'inverse, qui est très étrange.

La plus grosse difficulté des nombres complexes vient du fait qu'il est courant de définir i par i2=−1.

Ah okay ! $i$ est un nombre réel tel que $i^2 = -1$ ! La plus grosse difficulté vient du fait qu'il faut comprendre que l'application carrée ici considéré n'est pas l'application carrée "réelle". En effet, il est faux de dire qu'on étend par magie la fonction racine aux nombres négatifs (il n'est pas possible de rendre la fonction carrée bijective sur $\mathbb{R}$ sinon ça se saurait). Quand on écrit $i^2 = -1$, il ne s'agit donc pas de $x \mapsto x^2$ pour $x \in \mathbb{R}$. Cela reste une convention d'écriture car en réalité on note $i = (0, 1)$ et on a $i^2 = (0, 1) \times (0, 1) = (-1, 0) \in \mathbb{C} = \mathbb{R}\times\mathbb{R}$ (voir construction de $\mathbb{C}$ à partir du produit cartésien ci-avant et des opérations qui vont bien). L'application considérée est donc une fonction de $\mathbb{R}^2 \times \mathbb{R}^2$ dans $\mathbb{R}^2 = \mathbb{C}$. Je trouve bizarre d'introduire les complexes comme un couple de réels et ne plus jamais le traiter comme tel par la suite. Donc apprendre qui $i^2 = -1$ bêtement "parce qu'il faut s'y faire" sans plus de détails, bof bof. Le lecteur un peu curieux risque de rester sur sa faim. On ne définit pas $i$ autrement que comme le nombre imaginaire unité, qui en raison de l'opération de multiplication définie sur $\mathbb{R}\times\mathbb{R}$, donne $i \times i = -1$.

+1 -0

Bonjour,

J'ai quelques questions sur la manière de choisir le critère de convergence. Au lieu de choisir 2, qui va changer en changeant d'équation considérée, serait-il possible d'étudier l'évolution du module ? Si il décroit, ou reste constant, on va avoir convergence (en terme de module, je vois bien qu'une série $Z_{n+1}=Z_n*i$ ne vas pas converger, mais son module restera constant), sinon ça va diverger. Bon, je dis ça, mais j'ai essayé et ça ne fonctionne pas bien. Qu'est-ce que je rate ?

+0 -0

Je cherche une manière d'étudier la convergence un peu plus rigoureuse que de dire "Allons voir le 4ème terme de la série, et comparons le à une valeur choisie au petit bonheur la chance". Du coup, j'avais essayé d'utiliser le "Ratio test", sauf que je l'avais mal fait, et que je n'avais pas pris la limite, mais le ratio $a_2/a_1$, ce qui ne marchait pas.

La plupart des tests de convergence que je pourrais appliquer de manière générale (tous ?) semblent impliquer une limite, ce qui ne me plait que très moyennement. Du coup ma question, c'est de savoir si il existe un test qui marcherait pour n'importe quels $(a,b,c,d,..)$ avec $Z_{n+1}=a+bZ_n+cZ_n^2+dZ_n^3+...$.

Si un tel test n'existe pas, y a-t-il un moyen de choisir cette limite (2 dans ce tutoriel) de manière automatisée ?

+0 -0

Pour un polynôme, le seul point fixe attractif indépendant du choix des coefficients (pour peux qu'il y en ait un non nul sur un degré non nul) est le point à l'infini. Dans le cas présent, à partir de $2$ on peut montrer qu'on part à l'infini.

Ce que j'ai du mal à saisir dans ta question, c'est comment tu recolles la convergence de séries à la convergence d'une suite définie par récurrence.

Si un tel test n'existe pas, y a-t-il un moyen de choisir cette limite (2 dans ce tutoriel) de manière automatisée ?

Pas à ma connaissance. À priori des cycles attractifs peuvent apparaître partout dans $\mathbf{C}$.

+0 -0

Bonjour,

je n’ai pas tous à fait fini de lire ce tutoriel mais j’ai cependant quelques questions:

  • tout d’abord, il est évoqué soudainement l´argument c qui n´a été exprimé nul part et qui en plus de cela, semble se comporter, du moin là où j’en suis, comme z. D’après ce que j’ai vu sur une vidéo YT, le paramètre c devrait être un nombre arbitraire de préférence en dessous de 1.
  • Ensuite, pourquoi s’embêter avec c_r, c_i, z_i et z_r quand x et y suffisent ?
  • Pour finir, je trouve que la démarche n’est pas simplifié : il suffirait d’appliquer la formule z^2 + c à une large gamme de nombre complexe 50 fois par exemple et de l’afficher si il ne tend pas vers l’infini, nan ?

Cordialement.

+0 -0
  • Pourquoi tu dis que c n’est défini nulle part ? Au début de l’algorithme il est défini comme le complexe x + iy.
  • Dans un langage sans support natif des nombres complexes il faut les décomposer en deux réels. Et là comme tu as 2 nombres complexes il faut donc 4 réels.
  • Il me semble que c’est justement cette formule qui est appliquée.
+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte