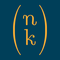Si vous avez fait un peu de mathématiques, vous connaissez peut-être les coefficients binomiaux, notés , pour deux entiers naturels et , qui apparaissent dans la formule du binôme de Newton. Il existe aussi une généralisation assez directe de ces coefficients : les coefficients multinomiaux qui apparaissent dans la formule du multinôme de Newton.
Ces deux familles de coefficients sont utilisés pour faire de la combinatoire (plus précisément du dénombrement). Ce tutoriel présente brièvement les coefficients, puis explique le lien entre leur définition habituelle et leur interprétation pour le dénombrement, avant de conclure sur un exemple simple : un majorant du nombre de positions au morpion.
Une familiarité avec les coefficients binomiaux et le binôme de Newton est un prérequis important pour suivre aisément ce tutoriel, même si le contenu devrait rester accessible avec quelques efforts dans le cas contraire.
- Coefficients binomiaux, binôme de Newton et dénombrement
- Coefficients multinomiaux, multinômes et dénombrement
- Exemple : calcul d'un majorant pour le nombre de positions au morpion
Coefficients binomiaux, binôme de Newton et dénombrement
Les coefficients binomiaux sont des entiers notés , avec et deux entiers naturels, étant non-nul.
On peut les exprimer avec une formule relativement simple :
Formule du binôme de Newton
Les coefficients binomiaux apparaissent dans le développement des binômes de Newton, d’où ils tiennent leur nom. Un binôme de Newton est une expression de la forme avec un entier naturel.
Par exemple, pour , on peut vérifier que :
De même pour , on peut vérifier que :
Plus généralement, on a :
Je présente ici l’expression avec les factorielles en premier, mais en pratique la formule est issue du développement du binôme plutôt que l’inverse, notamment via le triangle de Pascal, ou de la relation associée.
Interprétation en termes combinatoires
À toute première vue, les coefficients binomiaux sont un simple résultat de calcul : on développe l’expression, on réduit les monômes et on voit combien il y en a. On peut cependant prendre un angle d’attaque combinatoire !
Choix possibles lors du développement
On peut voir l’opération de développement comme un choix de ou pour chaque parenthèse. Combien de fois je veux voir dans mon monôme, et combien de fois ? De combien de manière puis-je choisir mes parenthèses pour que ça arrive ?
Par exemple, pour , on a :
Développer en une fois reviens à choisir pour chaque parenthèse ou . Il suffit en fait de choisir les parenthèses où on prend , les autres étant alors automatiquement un choix de vu qu’il n’y a pas d’autre choix possible.
Si je veux former , comment puis-je procéder ? Je n’ai pas vraiment le choix, je dois choisir pour chacune des trois parenthèses : je choisis donc dans 3 groupes de parenthèses parmi 3, il n’y a qu’une manière de le faire, ce qui signifie que .
Ensuite, si je veux former , je dois choisir dans deux groupes de parenthèses parmi 3, ce qu’on note . La dernière est alors une parenthèse où on choisit . Il y a trois manières de le faire : les deux à gauche, les deux à droites ou les deux extrêmes.
On peut continuer comme ça, mais j’imagine que vous avez compris le principe : à chaque fois, on choisit parenthèses parmi les parenthèses.
Cela se généralise à tous les choix de ce type : est le nombre de manières de choisir éléments parmi éléments indiscernables. se lit d’ailleurs souvent « parmi », tout simplement.
Séquences équivalentes par permutation
Une autre interprétation se fait en termes de séquences équivalentes par permutation.
On peut en effet voir le développement comme la formation de toutes les séquences possibles de la forme , avec correspondant à ou . Quand on développe mécaniquement, sans réarranger les termes, on forme ainsi toutes les séquences possibles de cette forme.
Par exemple, pour :
Quand on procède ainsi, on laisse plein de termes qui pourraient se factoriser. On peut le faire en comptant les ordres équivalents par permutation, car c’est ce qui va former le coefficient quand on factorise.
Si chaque lettre était différente, on aurait ordres possibles (par exemple , , etc.). Cela correspond au nombre de permutations de éléments distincts.
Ce faisant, on surestime le nombre de termes. Si on a fois dans un terme, on a en fait ordres identiques quand on ne peut plus distinguer les différents . On réduit ainsi à ordres différents.
Pour avoir le bon nombre de termes effectivement présents dans la somme, il faut faire de même pour , qui est présent fois si est présent fois et donc on aboutit à la formule du coefficient binomial :
Coefficients multinomiaux, multinômes et dénombrement
Que se passe-t-il si on n’a plus affaire à un binôme, mais un multinôme ?
On peut définir des coefficients multinomiaux :
avec .
Formule du multinôme de Newton
Les coefficients multinomiaux jouent le même rôle que les coefficients binomiaux dans la formule du multinôme de Newton, qui généralise celle du binôme.
On a ainsi :
avec les coefficients multinomiaux définis comme ci-avant.
Par exemple, on peut développer .
C’est bien une formule de généralisation, on retrouve la formule du binôme de Newton pour . Les coefficients binomiaux sont en fait les .
Interprétation combinatoire
Le coefficient multinomial peut s’interpréter similairement à celle du binôme de Newton, tout en généralisant.
Choix d’éléments pour former des groupes
On peut voir le coefficient multinomial comme le nombre de manières de former groupes de respectivement , , …, et éléments, choisis parmi éléments et tels que tout élément soit dans un des groupes (car la somme des vaut ).
Quand on regarde le trinôme suivant :
Par exemple, pour compter le nombre d’apparitions de , il faut voir qu’on peut soit prendre dans la première parenthèse, dans le deuxième et dans la troisième, ou alors n’importe quelle permutation de ces choix ( dans la deuxième, dans la première et dans la troisième, etc.), ce qui fait 3! = 6 possibilités, qui est bien le coefficient en question.
Autre exemple, pour compter les , il faut choisir dans deux des parenthèses et dans la troisième. Comme il y a 3 manières de choisir deux parenthèses parmi 3, on trouve que le coefficient est 3, ce qui est bien correct vis-à-vis de la formule.
Ce raisonnement en termes de choix se généralise pour tout multinôme, et généralise aussi l’interprétation faite pour le binôme de Newton.
Séquences équivalentes par permutations
Similairement à l’interprétation faite pour les coefficients binomiaux, on peut faire une interprétation en termes de permutations.
C’est tellement similaire que je serais très bref : il y a ordres possibles pour des séquences à lettres distinguables, et on divise ensuite par les , puis , etc. pour retirer les comptages multiples.
On retombe sur nos pattes !
Exemple : calcul d'un majorant pour le nombre de positions au morpion
Le jeu du morpion est très simple : chaque joueur pose un pion (croix ou cercle) à tour de rôle sur une case vide dans une grille 3×3, le premier qui aligne 3 pions en ligne, colonne ou diagonale a gagné. Si personne n’aligne de pion lorsque la grille est complète, il y a match nul.
J’appelle position l’état de la grille après chaque coup. Une manière de voir une position est comme une séquence de 9 éléments, chaque élément étant pris dans l’ensemble (0 pour vide, 1 pour le joueur 1 et 2 pour le joueur 2).
Tous les nombres d’éléments ne sont pas compatibles, il faut qu’ils respectent la succession des coups :
- on a d’abord 9 éléments vides (0),
- ensuite, on a 8 vides et un joueur 1,
- ensuite, on a 7 vides, un joueur 1, et un joueur 2,
- ensuite, on a 6 vides, deux joueurs 1 et un joueur 2,
- etc.
On va oublier les conditions de victoire et compter le nombre de positions qui respectent cette succession de coup. Ce sera donc un majorant du nombre réel de positions.
On peut assez naturellement interpréter chaque étape du jeu comme une sélection de cases où placer les éléments dans la grille : combien y a-t-il de manières de choisir des cases pour placer les X vides, Y joueur 1 et Z joueur 2, pour les X, Y, Z décrits ci-dessus ?
C’est une application directe du multinôme en termes de dénombrement.
| Vide | Jetons 1 | Jetons 2 | Formule du majorant | Valeur du majorant |
|---|---|---|---|---|
| 9 | 0 | 0 | 1 | |
| 8 | 1 | 0 | 9 | |
| 7 | 1 | 1 | 72 | |
| 6 | 2 | 1 | 252 | |
| 5 | 2 | 2 | 756 | |
| 4 | 3 | 2 | 1260 | |
| 3 | 3 | 3 | 1680 | |
| 2 | 4 | 3 | 1260 | |
| 1 | 4 | 4 | 630 | |
| 0 | 5 | 4 | 126 | |
| Total | - | - | - | 6046 |
Et voilà, j’espère que vous avez maintenant une meilleure compréhension des coefficients binomiaux et multinomiaux en terme de combinatoire !
Références
- Formule du binôme de Newton, sur Wikipédia.
- Formule du multinôme de Newton, sur Wikipédia.