La théorie cinétique des gaz

La matière se rencontre généralement sous trois états différents, à savoir solide (comme votre ordinateur), liquide (comme l’eau ou bien le mercure à température ambiante) et gazeux (comme l’air). C’est le cas des gaz qui nous intéresse ici.

Un gaz est constitué de nombreuses particules qui interagissent peu entre elles et occupe spontanément tout l’espace disponible. On peut décrire le comportement de chaque particule à l’aide de la théorie newtonienne, et donc déduire de la position des particules à un instant la position qu’elle auront à tout autre instant.

La théorie cinétique des gaz vise à relier le comportement microscopique des particules (vitesses et positions des particules, interactions entre les particules…) au comportement macroscopique du gaz (pression, températures, volume…). On sait, par l’observation, que ce comportement est indépendant de la nature des gaz ; comprendre par là qu’un gaz de O₂ et de H₂ se comporte pareil et a, entre autre, la même densité en nombre de particules par unité de volume.

Le comportement macroscopique typique des gaz dilué est la loi des gaz parfaits,

$PV = NkT$

où P est la pression du gaz, V son volume, T sa température (en kelvins¹), N le nombre de particules et k une constante², qui vaut 1,38.10^-23 J K^-1. On peut retrouver cette loi empiriquement en combinant de nombreuses lois de transformation. On va la retrouver ici en modélisant le comportement des particules du gaz.

Nous allons maintenant appliquer la mécanique newtonienne aux particules (atomes ou molécules) qui composent notre gaz afin de retrouver la loi du gaz parfait et d’en apprendre un peu plus sur le comportement microscopique d’un gaz.

• Simplifions le problème
• Collisions entre particules
• Collisions entre les particules et la paroi
• Température, énergie et formule du gaz parfait.

Simplifions le problème

Notre problème est donc le suivant : sachant comment se comportent les particules¹ de gaz, que peut-on déduire sur les propriétés macroscopiques de notre gaz ? Rappelons qu’il y a environ 10²⁵ particules dans un mètre cube de gaz, soit 10 millions par micromètre cube. C’est beaucoup. Il n’est pas possible de calculer ou simuler par ordinateur les lois de la mécanique newtonienne pour autant de particules. Il faut simplifier notre problème.

D’abord, on suppose que nos particules sont de petits objets sphériques. Leur taille sera assimilée à celle d’un atome de 10^-10 m (soit 0,1 nanomètre)². Cette simplification risque d’être infondée dans le cas de grosses particules, mais elle est réaliste dans le cas de la plupart des gaz.

La plus grosse simplification nécessaire est celle liée aux interactions : comment nos particules interagissent-elles, et quelles sont les interactions négligeables ? On distingue deux types d’interactions, les interactions à longue portée et celles à courte portée.

Les interactions à longue portée regroupent toutes les interactions dont l’intensité décroit lentement avec la distance. Cela inclut notamment la gravitation (complètement négligeable dans le cas de nos particules, très légères³) et certains effets électromagnétiques. On considère que nos particules ne sont pas chargées, et on néglige donc les effets électromagnétiques. De manière générale, les effets à longue portée sont très compliqués à prendre en compte, car une particule située loin aura quand même une influence, si bien que de très (de trop) nombreuses particules auront une influence.

Les interactions à courte portée regroupent les interactions dont l’intensité décroit rapidement avec la distance, ou n’ont d’effet perceptible qu’en deçà d’une certaine distance ; typiquement, certaines interactions électromagnétiques (force de Debye ou de Keesom). Elles sont faibles et participent à la cohésion de la matière à l’échelle moléculaire ou cristalline. À très courte distance (de l’ordre de la taille des particules), la force électromagnétique est très importante et provoque une forte répulsion. On peut ainsi approximer cette force par une collision : elle est nulle lorsque les particules sont éloignées, et infinie lorsqu’il y a contact.

Finalement, on émet l’hypothèse simplificatrice que nos particules n’interagissent que via des collisions. Toutes les autres interactions possibles seront négligées.

Pour que cette hypothèse reste réaliste, il faut que notre gaz soit dilué, c’est-à-dire que les particules soient éloignées les unes des autres, si bien que toutes les éventuelles interactions à courte portée soient négligeables, sauf quand les particules s’approchent et réalisent une collision, ce qui reste un évènement rare. De plus, il ne faut aucune interaction à longue portée présente dans le système ; typiquement, si nos particules sont chargées, elles vont interagir via des forces électromagnétiques. Sous cette condition de gaz dilué, les collisions ne font jamais intervenir plus de deux particules.

Ces collisions seront de plus des collisions élastiques. Cela signifie que l’énergie cinétique du système avant et après la collision est la même. Dans le cas d’une collision à deux particules,

$\left\{ E_1 \right\}_{\text{avant}} + \left\{ E_2 \right\}_{\text{avant}} = \left\{ E_1 \right\}_{\text{après}} + \left\{ E_2 \right\}_{\text{après}}$

où E_i désigne l’énergie cinétique de la particule i.

Le modèle à présent défini est celui dit des sphères dures. De petites boules de matière interagissent entre elles via des collisions élastiques, et uniquement ainsi. Ce modèle est réaliste pour représenter un gaz dilué.

Pour finir, on suppose que notre système n’a pas de direction privilégiée. Autrement dit, si on regarde ce qui se passe d’un côté et ce qui se passe de l’autre, on voit la même chose ; il y a autant de particules qui se déplacent vers la droite que vers la gauche⁴, quelle que soit la manière dont on a défini notre repère, idem pour toutes les grandeurs physiques. On parle d'isotropie⁵.

Avant de commencer à étudier plus concrètement notre problème, il y a une hypothèse de taille qui a été faite très rapidement : la matière est constituée de particules. Cette hypothèse est aujourd’hui très bien étayée (c’est l’hypothèse atomique), et personne ne songe à la remettre en question, mais ça n’a pas toujours été le cas. Quand la théorie cinétique des gaz a été créée, cette hypothèse n’était pas encore validée.

Même sous ces conditions pourtant hautement simplificatrices, il est impossible de simuler ne serait-ce qu’un mètre cube d’air, car cela représente un calcul bien trop lourd. Heureusement, nous allons pouvoir dérouler la théorie et faire des calculs analytiques pour relier les grandeurs microscopiques à d’autres, macroscopiques.

Collisions entre particules

Dans tout ce qui suit, on notera $\vec{v}_i$ la vitesse de la particule i, $||\vec{v}_i||$ le module de la vitesse de la particule i et v la moyenne du module de la vitesse des particules. La vitesse est un vecteur ; de par l’isotropie, il n’y a aucune direction privilégiée, si bien que la vitesse moyenne est nulle, même si la vitesse instantanée d’une particule est non nulle. On travaille donc avec le module de la vitesse, dont la moyenne est identique quelle que soit la direction de la particule. Ainsi, pour N particules,

$\frac{1}{N} \sum_i \vec{v}_i = \vec{0} \text{ et } v = \frac{1}{N} \sum_i ||\vec{v}_i|| \neq 0 .$

On notera aussi a le rayon des particules et n la densité volumique du gaz (nombre de particule par m³).

Pour commencer, on va s’intéresser à ce qu’il se passe entre deux collisions. On définit ainsi le libre parcours moyen ℓ comme la distance moyenne parcourue par une particule entre deux collisions. Si le temps moyen entre deux collisions est Δt, on a naturellement ℓ = v Δt. Essayons d’aller plus loin.

Il y a collision entre deux particules lorsque la distance entre leur centre vaut 2a. En effet, chaque particule ayant un rayon de taille a, les deux particules entrent en contact quand la distance entre leur centre devient égale à 2a.

On peut traiter le problème en considérant que l’on a une particule (que l’on qualifiera de virtuelle) de rayon 2a et que les autres sont ponctuelles. Dans le schéma ci-dessus, il y aura collision si un centre rentre dans la boule en pointillé, qui délimite la particule virtuelle. Notez que nous sommes toujours dans l’espace, à 3 dimensions, il s’agit bien de boules et non de disques.

On définit alors la section efficace σ¹, qui est l’aire balayée par cette particule virtuelle lors de son trajet. Cette aire est l’aire de la section maximale de la particule perpendiculairement à la direction de son mouvement. Dans le cas d’une boule, la section maximale est un disque de même rayon que la boule. On a alors σ = π (2a)². Ainsi, le volume dans lequel la particule fait des collisions est la section efficace multipliée par la distance parcourue.

Supposons qu’une seule particule se déplace, et que toutes les autres sont fixes. Par définition, la particule va subir une collision en moyenne quand elle se déplace de ℓ. Le volume moyen parcouru entre deux collisions, noté W, est ℓ σ. Or, on connait le nombre moyen de particules théoriquement présentes dans ce volume via la densité : nW, qui doit donc être égal à 1 (car il y a en moyenne une collision quand la particule parcourt la distance ℓ). Finalement,

$nW = 1, W = \ell \sigma \text{, d'où } \ell = \frac{1}{n \sigma} .$

Là, nous pouvons être très contents. En effet, on sait qu’il y a 2.10²⁵ particules dans un mètre cube de gaz et qu’une particule fait 10^-10 m de rayon. Je vous invite à faire vous-même l’application numérique pour ℓ.

Vous remarquerez que le libre parcours moyen, bien que petit, est très grand devant la taille des particules. En effet, le rapport ℓ/a vaut plus de 1000 ! Rapporté à l’échelle humaine, si un grand nombre d’humains se déplaçaient en ligne droite, il faudrait parcourir plusieurs kilomètres pour rencontrer quelqu’un.

La vitesse des particules vaut environ 1,8.10³ m/s à température ambiante (on calculera une valeur approchée de cette vitesse par la suite). On peut donc réutiliser la formule ℓ = v Δt et en déduire que Δt est de l’ordre de 2.10^-10 s. Cela signifie que le temps entre deux collisions pour une particule est inférieur à 1 nanoseconde. Si l’on repasse à un mètre cube de gaz, le nombre de collisions par seconde est gigantesque (n’hésitez pas à le calculer :) ).

Les valeurs obtenues nous disent que les particules sont très espacées les unes des autres, si bien qu’un instantané de notre gaz paraitrait fortement dilué. Cependant, les vitesses des particules et le nombre de particules sont tels que les collisions sont extrêmement fréquentes au sein du gaz.

D’un point de vue macroscopique, le libre parcours moyen est relié au coefficient de diffusion² par la relation $D = \frac{\ell v}{3}$, c’est-à-dire que le coefficient de diffusion est proportionnel au libre parcours moyen. Le coefficient de diffusion apparait macroscopiquement entre autre dans le cas où il existe une différence de densité ou de concentration (voir la la loi de Fick). Ainsi, plus le libre parcours moyen est grand, plus la matière diffuse, et donc s’homogénéise, rapidement.

Collisions entre les particules et la paroi

Jusqu’ici, les particules se frappaient les unes les autres, en se baladant dans un espace de taille infinie, ce qui n’est pas très réaliste. Ajoutons donc des parois, mettons nos particules en boite. Comme précédemment, il va y avoir des collisions, cette fois-ci avec la boite, et non plus seulement entre particules. Soit, mais quelles sont les conséquences de ces nouvelles collisions ?

En physique, certaines grandeurs se doivent d’être conservées au cours du temps. Parmi elles, la quantité de mouvement. La quantité de mouvement, notée $\vec{p}$, est une grandeur vectorielle définie par $\vec{p}=m \vec{v}$ ; pour nous, chaque particule aura la même masse m. Si le système considéré est composé de plusieurs objets indicés i, il faut sommer la quantité de mouvement de chacun d’entre eux. $\vec{p}_{\text{système}} = m \sum_{i} \vec{v}_{i}$. Ce sera cette grandeur qui sera conservée.

Considérons donc une particule qui se dirige perpendiculairement à une paroi et rebondit dessus sans se déformer via une collision élastique¹.

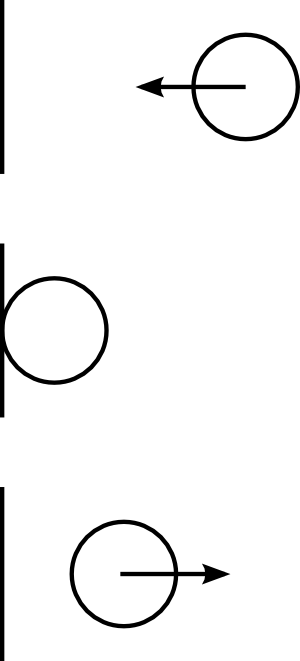
La quantité de mouvement du système avant le choc est $m\vec{v}_{\text{initiale}}$. On considère que la paroi est immobile, donc sans quantité de mouvement. On a fait l’hypothèse d’une collision élastique, donc la particule rebondit et repart dans la direction opposée avec la même vitesse.

En effet, il y a conservation de l’énergie cinétique, donc à masse constante, on doit avoir conservation du carré du module de la vitesse. Les symétries doivent être conservées² ; le système est symétrique haut/bas ainsi que devant/derrière, donc la particule est contrainte à rester sur sa ligne perpendiculaire au mur. Mais la particule n’a pas le droit de traverser le mur. La seule solution restante est bien que la particule reparte en sens opposé, avec le même module de vitesse.

Après le choc, la quantité de mouvement de la particule est donc $m\vec{v}_{\text{finale}} = -m\vec{v}_{\text{initiale}}$. Comme la quantité de mouvement totale du système est conservée, la différence de quantité de mouvement, $2m\vec{v}_{\text{initiale}}$, entre avant et après le choc a forcement été transférée dans la paroi. Chaque collision entre une particule et la paroi confère donc à la paroi une quantité de mouvement de $2m\vec{v}_{\text{initiale}}$.

Faisons maintenant cela pour chaque collision afin de connaitre l’effet total des collisions sur la paroi. On va donc considérer un flux de particules. Chaque particule aura une vitesse potentiellement différente, mais la même masse et, pour simplifier, toutes iront perpendiculairement à la paroi. Rappelons qu’on fait comme si les particules ne se frappaient pas les unes les autres dans cette partie. Prenons une densité n. La particule i se déplace à la vitesse $\vec{v}_i$. On s’intéresse au nombre de particules qui va toucher la paroi entre les temps 0 et t.

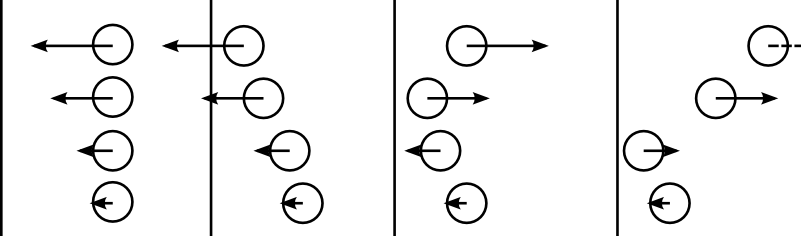
Une particule va toucher la paroi si la distance qu’elle parcourt durant ce temps est au moins la distance entre la particule et la paroi. Or, la particule i parcourt $t\:||\vec{v}_i||$ durant le temps t, donc toute particule i située à une distance inférieure à $t\:||\vec{v}_i||$ va cogner la paroi. La distance considérée dépend donc de la vitesse de la particule : si une particule est loin mais rapide, elle atteindra la paroi au même titre qu’une particule proche mais lente.

Chaque particule i située à une distance $t\:||\vec{v}_i||$ ou inférieur de la paroi va frapper la paroi, et ce sur toute la surface S de la paroi. Cela conduit à un volume dans lequel toute particule va frapper la paroi d’ici le temps t, $tS\:||\vec{v}_i||$, d’où un nombre de particule $tSn\:||\vec{v}_i||$. Finalement, comme chaque collision apporte la quantité de mouvement $2m\vec{v}_i$ au mur, l’ensemble des collisions lui apporte $2 m t S n \langle \vec{v}_i^2 \rangle \vec{e}_x$, où $\vec{e}_x$ est le vecteur unité suivant lequel les particules se déplacent, orienté vers l’extérieur de la boite et $\langle X \rangle$ désigne la moyenne de X sur les particules.

Le plus dur est fait ! Appliquons maintenant le principe fondamental de la dynamique, ou deuxième loi de Newton, aux particules :

$\sum \vec{F}_{\text{appliquée}} = m \frac{d\vec{v}}{dt}$

avec $\frac{d\vec{v}}{dt}$ la dérivée de $\vec{v}$ par rapport au temps.

Vous ne remarquez rien ? La quantité de mouvement n’a pas été introduite par hasard³, en effet $m \frac{d\vec{v}}{dt} = \frac{d\vec{p}}{dt}$ (car la masse est constante). Comme on connait la variation de la quantité de mouvement des particules due au contact avec la paroi, on peut facilement en déduire la force.

$\vec{F}_{\text{particules sur la paroi}} = 2 m S n \langle \vec{v}_i^2 \rangle \vec{e}_x .$

On est presque content. Presque, car cette force dépend de la surface de la paroi. Qu’à cela ne tienne, exprimons une pression plutôt qu’une force. Une pression est une force par unité de surface, c’est à dire une force appliquée sur une aire unité. Dans le cas d’un gaz dilué, on trouve donc

$P_{gaz} = 2 m n \langle \vec{v}_i^2 \rangle .$

On a ainsi une formule qui relie la pression à la vitesse des particules. Plus les particules vont vite, plus la pression sur les parois sera forte.

Température, énergie et formule du gaz parfait.

Nous avons maintenant presque toutes les données pour caractériser notre gaz. Pour finir, nous allons faire deux choses : déterminer l’énergie possédée par le gaz, due aux mouvements des particules, et chercher une équation d’état, c’est-à-dire une relation entre différents paramètres physiques qui déterminent l’état de notre gaz (l’équation d’état des gaz parfaits, ce serait tout de même tip top). L’intérêt d’une telle équation est de déterminer le comportement du gaz. Par exemple, si on a une équation d’état qui nous dit que lors d’une transformation à température constante, PV est constant¹, on pourra calculer les variations de la pression connaissant celles du volume.

L’énergie de notre système est due uniquement au mouvement des particules c’est-à-dire à leur énergie cinétique. Vous savez tous que l’énergie cinétique de la particule i vaut $E_{ci} = \frac{1}{2} m_i \vec{v}_i^2$. L’énergie cinétique moyenne est donc $\langle E_c \rangle = \frac{1}{2} m \langle \vec{v}_i^2 \rangle$. Si on note V le volume de gaz considéré (et de fait N = nV le nombre total de particules), sachant que toutes les particules ont la même masse, alors l’énergie totale du système, notée U, vaut

$U = n V \langle E_c \rangle = n V \frac{1}{2} m \langle \vec{v}_i^2 \rangle = \frac{3}{2} P V .$

Si l’utilité de l’énergie interne est facile à deviner (c’est l’énergie totale contenue dans notre système), celle de l’énergie cinétique moyenne est peut-être moins évidente : il s’agit de son lien avec la température. En effet, nous allons relier l’agitation des particules à une grandeur, nommée température cinétique et notée T, par la formule suivante

$\langle E_c \rangle = \frac{3}{2} k T.$

Ceci est la définition de la température, telle qu’elle a été posée par Krönig en 1856. k est la constante de Boltzmann, qui vaut approximativement 1,38.10^-23 J K^-1. Attention, si cette température est bien celle que vous mesurez avec un thermomètre (même grandeur physique), il faut l’exprimer en kelvins (unité différente). La température en kelvins est égale à la température en degrés Celsius moins 273,15 °C.

Cette définition signifie que la température est une mesure de la vitesse des particules. L’agitation des particules à l’échelle microscopique a comme conséquence macroscopique une grandeur physique, la température. La température est une grandeur qui n’a de sens que si on considère un grand nombre de particules : une particule possède une vitesse et une énergie cinétique, un gaz dispose d’une température. Cette association entre les mouvements microscopiques et la température est aussi valable pour les corps solides et liquides. On parle de manière générale d'agitation thermique.

Partant de l’énergie cinétique, on peut trouver la moyenne du carré des vitesses². Pour calculer la moyenne du module, il nous faudrait connaitre (ou faire une hypothèse) sur la distribution des vitesses. Comme cela nous emmènerait très loin, nous allons calculer la vitesse quadratique moyenne, v^*, définie comme $\sqrt{\langle \vec{v}_i^2 \rangle }$ (racine carrée de la moyenne du carré des vitesses). Cela se fait facilement à partir de l’énergie cinétique :

$v^* =\sqrt{ \frac{3}{m} k T}$

soit, à température ambiante (300 K), avec m de l’ordre de 2.10^-27 kg, de l’ordre de 2,5 km/s. Cela n’est pas la moyenne du module des vitesses ; le calcul de celle-ci, du même ordre de grandeur, nécessiterait des calculs et hypothèses plus complexes. En vérité, la moyenne du module des vitesses vaut approximativement 1,8 km/s³.

Il ne reste plus qu’à trouver notre équation d’état. Pour cela, on va réunir nos formules. Je rappelle qu’on a

$\langle E_c \rangle = \frac{U}{nV} = \frac{3}{2} k T$ avec $U = \frac{3}{2} P V.$

En remplaçant U dans la formule précédente, on trouve

$\frac{\frac{3}{2} P V}{nV} = \frac{3}{2} k T \Rightarrow P = n k T .$

En utilisant le nombre de particules N et le volume plutôt que la densité (N = nV), on retrouve l’équation d’état du gaz parfait :

$PV = N k T .$

Ainsi que l’énergie interne en fonction de la température $U = \frac{3}{2} N k T$.

Voilà. Nous venons de démontrer, dans le cadre d’un modèle simpliste, que les gaz dilués se comportent selon la loi des gaz parfaits. Bonne nouvelle, c’est cohérent avec l’expérimentation.

Qu’a-t-on fait finalement ? On a créé un petit modèle dans lequel des particules sphériques se déplacent dans toutes les directions sans préférence et étudié les conséquences des collisions de celles-ci, en supposant que les seules interactions possibles sont justement les collisions. On a retrouvé la loi des gaz parfaits (et même un peu plus), compatible avec l’expérimentation pour les gaz dilués.

Dans un tel modèle, l’énergie du gaz ne dépend que de sa température (ce qui n’est cependant valable que pour les gaz monoatomiques).

S’il n’y avait qu’une chose à retenir de ce tutoriel, ce serait la démarche. Poser des hypothèses crédibles, dérouler le modèle, chercher des lois pour notre système. Autrement dit, créer un modèle, une théorie physique.

S’il y avait une deuxième chose à retenir, ce serait ce qu’est un gaz à l’échelle de la particule. À savoir un milieu extrêmement dilué, dans lequel les particules passent la plus grande partie de leur temps à aller en ligne droite, avec de rares collisions ; cependant, les vitesses des particules et leur nombre sont tels que les collisions sont fréquentes au sein du gaz.

Les travaux présentés ici ont été réalisés au milieu du 19^e siècle, puis approfondi via la mécanique statistique par Boltzmann. À l’époque, l’hypothèse atomique était encore mal acceptée, et la théorie de Boltzmann guère prise au sérieux.

Les deux axes de suite à ce cours sont la mécanique statistique dudit Boltzmann et la thermodynamique, afin de faire quelque chose de l’équation d’état si durement obtenue.

Je souhaiterais remercier Blackline, Holosmos, klafyvel, Looping, Luthaf, Rockaround, Mewtow et Emel pour leurs commentaires lors de la bêta et Aabu pour la validation !

Annexe : libre parcours moyen sans l’approximation du mouvement unique

Nous avons supposé auparavant que seule une particule se mouvait, et que toutes les autres étaient fixes. Cela n’a aucune raison d’être vrai. En vérité, toutes les particules bougent dans toutes les directions, avec un module moyen de vitesse v et une vitesse quadratique moyenne v^*. Considérons deux particules, notées A et B, telles que la prochaine collision de A sera avec B et la prochaine collision de B sera avec A. En moyenne, la distance qu’elles auront parcourue depuis leur dernière collision sera ℓ.

Le référentiel dans lequel nous nous trouvons est actuellement celui du laboratoire². On peut, en appliquant une rotation à notre référentiel, et donc sans perdre aucunement en généralité, faire en sorte que la particule A se déplace uniquement selon l’axe x (la direction de A définit maintenant l’axe x). Le module moyen des vitesses est toujours v dans ce référentiel et la vitesse quadratique toujours v^*. Ce référentiel sera noté $\mathcal{R}_1$.

On peut aussi briser l’équivalence entre toutes les particules et dire, par une translation uniforme du référentiel $\mathcal{R}_1$, que la particule A est fixe. Ce référentiel sera noté $\mathcal{R}_2$. Ainsi, toutes les autres particules voient leur vitesse diminuée de celle de A. En notant $\left. v_A \right\rfloor_{\mathcal{R}_1}$ la vitesse de A prise dans le référentiel $\mathcal{R}_1$, on a

$\left. v_B \right\rfloor_{\mathcal{R}_2} = \left. v_B \right\rfloor_{\mathcal{R}_1} - \left. v_A \right\rfloor_{\mathcal{R}_1} .$

On peut ensuite décomposer la vitesse de B selon les axes x, y et z, sachant que la vitesse de A est selon l’axe x.

Comme la particule A a une vitesse aléatoire sans direction privilégiée, notre système reste isotrope en moyenne. En effet, même si le référentiel $\mathcal{R}_2$ n’est plus isotrope, la direction privilégiée est choisie selon A, donc aléatoirement ; l’isotropie est donc bien conservée en moyenne¹.

Calculons donc la vitesse de B dans $\mathcal{R}_2$. On notera $\vec{e}_x$ le vecteur unitaire selon l’axe x, et pareillement pour les autres axes.

$\left. \vec{v}_B \right\rfloor_{\mathcal{R}_2} = ( \left. v_{Bx} \right\rfloor_{\mathcal{R}_1} - \left. v_A \right\rfloor_{\mathcal{R}_1}) \vec{e}_x + \left. v_{By} \right\rfloor_{\mathcal{R}_1} \vec{e}_y + \left. v_{Bz} \right\rfloor_{\mathcal{R}_1} \vec{e}_z$

On veut la moyenne du module de cette grandeur. Commençons donc par le module (noté entre $||$).

$\left. ||\vec{v}_B || \ \right\rfloor_{\mathcal{R}_2} = \sqrt{( \left. v_{Bx} \right\rfloor_{\mathcal{R}_1} - \left. v_A \right\rfloor_{\mathcal{R}_1})^2 + (\left. v_{By} \right\rfloor_{\mathcal{R}_1})^2 + (\left. v_{Bz} \right\rfloor_{\mathcal{R}_1})^2}$

Malheureusement, on ne peut pas faire grand chose de cela. Heureusement, notre système est toujours isotrope.

Si la vitesse de chaque particule est multipliée par λ³, alors la vitesse quadratique moyenne et le module moyen des vitesses sont chacun multipliés par λ ; au contraire, si la vitesse quadratique moyenne ou le module moyen des vitesses est multiplié par λ, on ne peut rien conclure sur la vitesse dans le cas général.

Mais ici n’est pas le cas général, puisqu’il y a isotropie en moyenne. De par l’isotropie, pour que la vitesse quadratique moyenne soit multipliée par λ en passant du référentiel $\mathcal{R}_1$ à $\mathcal{R}_2$, il faut que chacune des composantes de la vitesse le soit en moyenne. Ainsi, le module moyen des vitesses sera lui aussi multiplié par λ, donc le libre parcours moyen aussi.

Or, nous pouvons calculer la vitesse quadratique moyenne, racine carrée de la moyenne du carré du module. Ainsi, nous pourrons calculer le facteur multiplicatif. Commençons par le carré du module.

Reconnaissons ici deux termes, $(\left. v_A \right\rfloor_{\mathcal{R}_1})^2$ et $(\left. v_{Bx} \right\rfloor_{\mathcal{R}_1})^2 + (\left. v_{By} \right\rfloor_{\mathcal{R}_1})^2 + (\left. v_{Bz} \right\rfloor_{\mathcal{R}_1})^2$ qui sont tous deux le carré du module des vitesses des particules A et B dans le référentiel $\mathcal{R}_1$. D’où

Reste le dernier terme qui pose problème. Heureusement, $\left. v_A \right\rfloor_{\mathcal{R}_1}$ et $\left. v_{Bx} \right\rfloor_{\mathcal{R}_1}$ sont indépendants, donc la moyenne du produit est le produit des moyennes. Or, par isotropie, $\langle \left. v_{Bx} \right\rfloor_{\mathcal{R}_1} \rangle = 0$. Finalement, on trouve la vitesse quadratique moyenne des particules, A exceptée.

$\left. v^* \right\rfloor_{\mathcal{R}_2} = \sqrt{2(v^*)^2} = \sqrt{2} v^*$

Le facteur multiplicatif est ici $\sqrt{2}$. De fait, en remplaçant v, on voit bien apparaitre le facteur $1/\sqrt{2}$. Nous concluons donc que le libre parcours moyen vaut

$\ell = \frac{v \Delta t}{\sqrt{2}} \ .$