Approximation des réels par les flottants

L’ensemble des réels présente quelques propriétés sympathiques : il est non borné, on trouve toujours un réel entre deux autres réels, et il contient un nombre infini d’éléments. Rien de tout cela n’est vrai pour les flottants binary64 :

• il existe un nombre fini de mantisses différentes, car elles sont codées sur un nombre fini de bits ;
• il existe pour la même raison un nombre fini d’exposants, et donc un nombre fini de flottants ;
• un nombre fini d’exposant signifie un exposant maximal et minimal, c’est-à-dire des bornes à l’ensemble des flottants en les associant respectivement aux mantisses maximales et minimales.¹

Bornes de l’ensemble des flottants

La représentation des flottants est parfaitement symétrique grâce au bit de signe. Les bornes dans les négatifs s’obtiennent donc en changeant le signe des bornes obtenues pour les positifs. Dans la suite, chaque nombre sera ainsi précédé du symbole $\pm$.

Plus grand flottant non infini (en valeur absolue)

Les plus grands flottants en valeur absolue sont les infinis (négatifs et positifs), qu’on représente avec la mantisse nulle et l’exposant à la valeur spéciale +1024. Cependant, les infinis ne sont pas des réels. Il vient alors la question suivante : quelle est le plus grand flottant non infini (en valeur absolue) ?

Pour obtenir la plus grande valeur non infinie, il faut prendre naturellement le plus grand exposant (+1023) et la plus grande mantisse possible pour cet exposant (c’est-à-dire une suite de 52 « un », en binaire). La partie entière, implicite, vaut 1. On obtient donc le flottant suivant, qui est la plus grande valeur représentable avec un flottant binaire double précision (binary64).

$\pm \Omega = \pm [1{,}11...1] \times 2^{1023} = \pm (2-2^{-52})\times 2^{1023} \approx \pm 1{,}798 \times 10^{308}$

Plus petit flottant non-nul (en valeur absolue)

Le plus petit flottant est évidemment zéro, qui est représenté par la mantisse nulle et un exposant à la valeur spéciale -1023. Quelle est la valeur directement supérieure, c’est-à-dire le plus petit flottant non-nul (en valeur absolue) ?

Nous laissons de côté les flottants dénormalisés, pour nous intéresser uniquement aux flottants normaux. Le plus petit flottant non-nul est alors celui dont l’exposant est le plus petit exposant (-1022), la partie entière implicite du significande vaut 1 et la mantisse est la plus petite mantisse normalisée (que des zéros).

$\pm \alpha = \pm [1{,}0...0] \times 2^{-1022} = \pm 2^{-1022} \approx \pm 2{,}225 \times 10^{-308}$

Précision des flottants

La précision correspond au nombre de chiffres du significande qu’il est possible de stocker. Par exemple, un format dans lequel on ne peut stocker que les dixièmes a une précision plus faible qu’un format où l’on peut stocker les dixièmes et les centièmes.

Pour les flottants, il s’agit donc du nombre de bits disponibles pour stocker la mantisse plus le bit implicite. Par exemple, la précision du format binary32 (23 bits de mantisse) est plus faible que celle du binary64 (52 bits de mantisse).

Le fait que le format binary64 stocke toujours le même nombre de bits pour la mantisse fait que la précision est constante quel que soit l’exposant.

La précision est liée directement à la répartition des flottants parmi les réels.

Répartition des flottants parmi les réels

Si un flottant normalisé s’écrit : $x = s \times 2^{e}$

alors les mantisses de ses deux plus proches voisins $x^+$ et $x^-$ s’obtiennent en incrémentant ou décrémentant la mantisse de 2^-52 : $s^\pm = s\pm 2^{-52}$

Ceci est vrai pour toutes les mantisses, l’écart reste constant. Par contre, l’écart entre deux flottants consécutifs augmente avec l’exposant. En effet,

$x^{\pm} = s^\pm \times 2^{e} = (s\pm 2^{-52}) \times 2^{e} = s \times 2^{e} \pm 2^{e-52} = x \pm 2^{e-52}$

Cela signifie que l’écart absolu entre deux flottants consécutifs (avec le même exposant $e$) vaut $2^{e-52}$.

Les flottants avec un grand exposant seront ainsi plus écartés les uns des autres, car le changement du dernier bit de la mantisse correspondra alors à un bond en avant de plusieurs milliers, millions, voire plus. Au contraire, pour les petits flottants, le changement du dernier chiffre après la virgule correspondra à un petit saut de quelques dixièmes, millièmes, etc. En somme, la densité des flottants diminue à mesure qu’on s’éloigne de zéro pour progresser vers l’infini.

Les deux figures ci-dessous montrent ce changement de densité, en montrant les flottants autour de 1 et de 2⁶⁴.

Pour une vision plus complète, voici les écarts entre flottants consécutifs sur un large intervalle de valeurs.

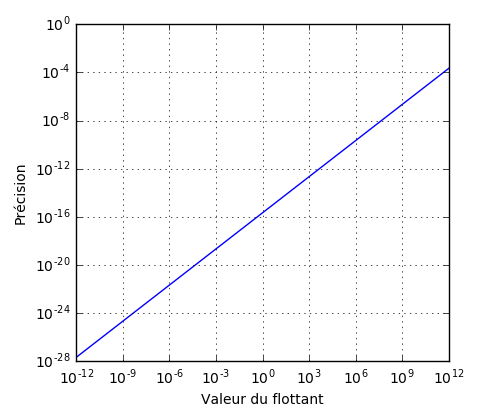
On peut noter que la différence entre deux flottants dénormalisés consécutifs est constante, étant donné qu’une seule valeur d’exposant est définie et que seule la mantisse varie.

Comme les flottants sont codés sur un nombre fini de bits, il y en a un nombre fini. Pour faire correspondre chaque réel, qui existent en nombre infini, à un flottant, il est donc nécessaire de faire des arrondis.

Modes d’arrondis

Liste des modes d’arrondis

La norme IEEE 754 définit deux familles d’arrondis et différents modes d’arrondi pour les formats binaires, tels que binary64 :

• les arrondis au plus proche :
  • au chiffre pair le plus proche,
  • au flottant le plus proche avec rupture des égalités au profit de la plus grande valeur absolue.
• les arrondis orientés :
  • vers zéro,
  • vers $+\infty$,
  • vers $-\infty$.

Chacun de ces modes présente différentes propriétés qui les rendent appropriés pour différents cas d’application.

Mode d’arrondi par défaut : l’arrondi au chiffre pair le plus proche

Bien qu’il soit possible de configurer les modes d’arrondi, le mode par défaut est utilisé dans la grande majorité des cas : il s’agit de l’arrondi au chiffre pair le plus proche. Ce mode présente le comportement suivant :

• Pour les réels plus grands que $\Omega$ en valeur absolue, on arrondit vers l’infini du bon signe (dépassement).
• Pour les réels plus petits que $\alpha$ en valeur absolue, la norme garantit le signalement d’un soupassement, mais rien de plus (voir plus loin).
• Pour le reste, on arrondit au plus proche, et en cas d’égalité, on arrondit vers le flottant avec le dernier bit de mantisse égal à zéro (arrondi au chiffre pair le plus proche).

Opérations d’arrondi

Arrondi des nombres très grands : dépassement

Tous les nombres supérieurs à $\Omega$ (en valeur absolue) seront arrondis vers un infini : on parle de dépassement, ou plus communément d'overflow. Par exemple, le nombre $-1{,}8 \times 10^{308}$ est hors-limite, il sera arrondi vers l’infini.

>>> -1.8e308  # inférieur à -1.798e308
-inf

Arrondi des nombres très petits : soupassement

Quand un nombre est inférieur à $\alpha$, on parle de soupassement, ou plus communément d'underflow. Le fonctionnement est un peu plus délicat que pour le dépassement. En effet, une certaine liberté est laissée au langage qui implémente la norme.

En général, lorsqu’un nombre est inférieur à $\alpha$, il va être stocké sous forme dénormalisée, par arrondi au chiffre pair le plus proche (voir plus loin). Les nombres inférieurs à $\varepsilon$ seront arrondis vers zéro. Par exemple, $10^{-324}$ est arrondi vers zéro.

>>> 1e-324  # Exactement zéro pour l'ordinateur
0.00000000000000000e+00

Finalement, la droite des réels est coupée au deux bouts, et tout ce qui dépasse est arrondi vers l’infini. Au milieu, même combat, le zéro s’étale sur les nombres trop petits qui l’environnent.

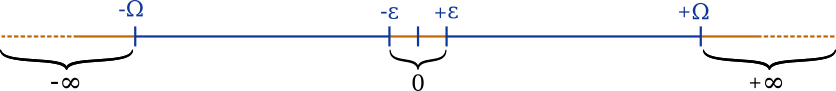
Arrondi usuel : arrondi au chiffre pair le plus proche

Lorsqu’un réel ne coïncide pas directement avec un flottant, mais qu’il n’est pas hors limite, il est arrondi au flottant le plus proche, c’est-à-dire qu’il sera arrondi vers le flottant le moins éloigné de lui sur la droite des réels. En cas d’égalité de distance, on prend le flottant avec le dernier bit de la mantisse nul (arrondi au chiffre pair le plus proche). En pratique, chaque flottant représente tout un intervalle de réels.

La figure ci-dessous illustre ce phénomène. Trois flottants consécutifs $a$, $b$ et $c$ sont représentés. Tous les réels entre $\frac{a+b}{2}$ et $\frac{b+c}{2}$ sont arrondis vers le même flottant $b$.

En programmation, un arrondi est fait lors de l’affectation d’une valeur littérale à une variable. La valeur littérale représente un réel, et elle doit être arrondie pour être stockée dans la variable sous forme de flottant. Par exemple, regardez le code ci-dessous.

>>> x = 0.99999999999999999
>>> y = 1.00000000000000001
>>> x == y
True

Les valeurs littérales $0{,}99999999999999999$ et $1{,}00000000000000001$ sont converties en flottants lors de l’affectation. Pour ces deux valeurs, le flottant le plus proche est $1$, donc un arrondi est fait. On a en fin de compte $x = y = 1$.

Autre exemple plus gênant, certains nombres « simples » subissent des arrondis, visibles lorsqu’on affiche suffisamment de décimales. Par exemple, le réel $0{,}1$ n’est pas représentable de manière exacte (aucun flottant n’est égal à $0{,}1$) et est arrondi.

>>> 0.1
1.00000000000000006e-01

Quelle est l’erreur d’arrondi faite dans des cas comme ça ? La réponse se trouve dans la partie suivante.

Dans la section précédente, nous avons vu que les réels étaient arrondis par défaut au flottant le plus proche. Au cours de ce processus, une erreur d’arrondi est faite.

Définition de l’erreur d’arrondi

L’erreur d’arrondi est l’écart entre le réel de départ et le flottant vers lequel il est converti lors de l’opération d’arrondi. Si on note $r$ le réel de départ, $f$ le flottant résultant de l’arrondi et $\delta$ l’écart entre les deux, cette définition se traduit par la relation suivante :

$r = f + \delta$

Le schéma ci-dessous met en image la relation précédente.

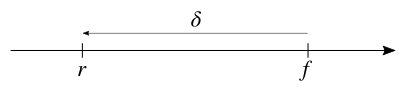
L’erreur d’arrondi exacte dépend du réel subissant l’arrondi, mais il est en général possible d’en donner un majorant.

Erreur d’arrondi maximale pour un flottant donné

Sur l’intervalle compris entre le plus grand flottant positif $+\Omega$ et le plus grand flottant négatif $-\Omega$, il est possible d’estimer l’erreur d’arrondi maximale, qui est fonction du réel arrondi. En dehors de cet intervalle, l’erreur peut être arbitrairement grande, puisqu’on a affaire au phénomène de dépassement.

Chaque flottant de l’intervalle $\mathopen{]}-\Omega\,;+\Omega\mathclose{[}$ est encadré par un prédécesseur direct et un successeur direct. Pour un flottant $f$, si on note $f^-$ son prédécesseur direct et $f^+$ son successeur direct, on a la relation suivante :

$f^- < f < f^+$

Dans le mode d’arrondi au plus proche, les réels compris entre $\frac{f^- + f}{2}$ et $\frac{f + f^+ }{2}$ seront arrondis vers $f$.

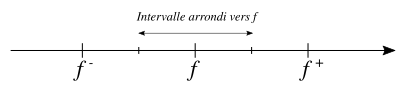
On peut ainsi estimer l’erreur d’arrondi maximale. Si un réel $r$ est arrondi vers un flottant $f$, alors l’erreur d’arrondi est au plus en valeur absolue :

$|\delta_{max}| = \left|\frac{f^+ - f}{2}\right|= \left|\frac{f^- - f}{2}\right|$

Il ne reste plus qu’à expliciter $f^+$ et $f^-$ en fonction de $f$ pour calculer une valeur numérique de cette erreur.

Valeur de l’erreur d’arrondi maximale en fonction du flottant

Prenons un flottant $f$ de la forme :

$f = s \times 2^{e}$

Le successeur direct de $f$, $f^+$, est obtenu en incrémentant le dernier bit du significande de $f$. Son significande $s^+$ est ainsi égal à :

$s^+ = s + 2^{-52}$

Le prédécesseur direct de $f$, $f^-$, est obtenu de manière similaire, mais en décrémentant le dernier bit du significande de $f$. Son significande $s^-$ vaut alors :

$s^- = s - 2^{-52}$

On peut alors utiliser la formule du paragraphe précédent pour calculer l’erreur d’arrondi maximale :

$|\delta_{max}| = \frac{s - s^-}{2} \times 2^e = \frac{s^+ - s}{2} \times 2^e = 2^{-53} \times 2^e$

On a donc une erreur d’arrondi d’au pire $2^{-53}$ sur le significande. L’erreur sur le flottant dans son ensemble dépend de l’exposant $e$ et vaut au plus $2^{e-53}$.

Exemples d’application

Estimer l’erreur d’arrondi pour un réel donné

Si l’on a un nombre, qui n’est potentiellement pas représentable de manière exacte, quelle est l’erreur maximale d’arrondi qui sera faite ? Prenons pour exemple le réel $2,2$, qui subira un arrondi lors de sa conversion en flottant.

La première étape pour estimer l’erreur d’arrondi maximale consiste à trouver l’exposant. Pour cela, il suffit d’encadrer le nombre entre deux flottants d’exposants consécutifs :

$2^1 \leq 2{,}2 < 2^2$

L’exposant qu’aura $2,2$ une fois converti en flottant est donc $1$. Il suffit maintenant d’appliquer la formule vue précédemment pour obtenir l’erreur maximale :

$|\delta_{max}| = 2^{e-53} = 2^{1-53} = 2^{-52} \approx 2{,}22 \times 10^{-16}$

Il est également possible de calculer la véritable erreur d’arrondi, par exemple à l’aide d’un calculateur en précision arbitraire. On obtient approximativement la valeur suivante :

$|\delta| = 1{,}78 \times 10^{-16} < \delta_{max}$

L’erreur exacte est donc bien inférieure à l’erreur maximale. Tout va bien !

Encadrer un résultat

À l’issue d’une opération quelconque entre deux flottants, on obtient comme résultat un certain flottant $f$, issu de l’arrondi du résultat exact. Dans quel intervalle se trouvait nécessairement le résultat exact, avant d’être arrondi ?

Supposons qu’on ait obtenu pour résultat la valeur arrondie $0{,}375$. Pour trouver l’intervalle où se trouvait la valeur exacte, il faut d’abord convertir ce nombre en notation scientifique. On obtient $1{,}5 \times 2^{-2}$.

Comme l’exposant est désormais connu, il suffit d’appliquer la formule vue plus haut donnant la valeur maximale de l’erreur d’arrondi. On trouve $\delta_{max} = 2^{-2-53} = 2^{-55}$. Ainsi, le résultat exact se trouvait nécessairement entre $0{,}375-2^{-55}$ et $0{,}375+2^{-55}$.