Fonctions numériques

Nombres solitaires ou nombre serrés

Les ensembles de nombres classiques se divisent généralement en deux grandes catégories :

• Les ensembles discrets : ce sont les ensembles dans lesquels les nombres sont isolés les uns des autres. Par exemple dans les entiers, chaque nombre possède un suivant qui est éloigné de lui d’une distance 1 et il n’y a pas d’autres nombres entiers entre les deux. Les deux ensembles discrets les plus courants sont $\mathbb{N}$ et $\mathbb{Z}$.
• Les ensembles continus : ce sont les ensembles dans lesquels les nombres sont agglutinés les uns aux autres et chaque nombre possède une infinité de voisins qui sont aussi proches de lui que l’on veut. L’ensemble continu le plus courant est $\mathbb{R}$, mais il faut aussi faire entrer dans cette catégorie tous les intervalles réels tels que $[-1,1]$ par exemple ou encore l’ensemble $\mathbb{C}$ des nombres complexes.

À partir de là, les fonctions numériques se classent selon leur ensemble de départ.

• Si l’ensemble de départ est discret, alors la fonction se nomme une suite.
• Si l’ensemble de départ est continu, alors la fonction se nomme… une fonction.

Il n’existe pas de terme particulier pour désigner une fonction dont l’ensemble de départ est continu. Selon les cas on peut parler de fonction réelle ou de fonction complexe, mais il est fréquent qu’on utilise le mot fonction sans autre précision. En revanche, si l’ensemble de départ est discret, il faut bien utiliser le mot suite pour éviter toute confusion.

Notations

Les fonctions (dont l’ensemble de départ est continu) se notent de façon classique comme nous l’avons vu dans le chapitre précédent :

Pour les suites en revanche, il y a quelques petites variations. Regardez :

Avez-vous repéré les quatre différences ?

• Premièrement, l’ensemble de définition n’est évidemment plus $\mathbb{R}$, mais $\mathbb{N}$ puisqu’il s’agit d’une suite.
• Deuxièmement, la suite est notée par la lettre $u$ à la place de $f$. Si on avait plusieurs suites on noterait les suivantes $v$ et $w$.
• Troisièmement, la variable se nomme $n$ au lieu de $x$. Ceci est normal, puisque c’est l’usage en maths de noter les nombres entiers avec cette lettre.
• Et quatrièmement, l’image de $n$ par $u$ n’est pas notée $u(n)$ avec des parenthèses, mais $u_n$ avec la variable en indice.

Bon, ce ne sont que quelques petites variations de notation qui ne changent rien sur le fond. On s’y habitue par la pratique.

Il n’est pas toujours très facile d’y voir clair dans le mécanisme d’une suite ou d’une fonction à partir de sa définition. Pour remédier à cela, il existe une façon bien commode de les représenter et qui permet d’avoir en un coup d’œil une idée de leur fonctionnement : leur graphe.

Pour tracer le graphe d’une fonction, il faut tout d’abord disposer d’un repère, c’est-à-dire deux axes gradués, l’un horizontal et l’autre vertical :

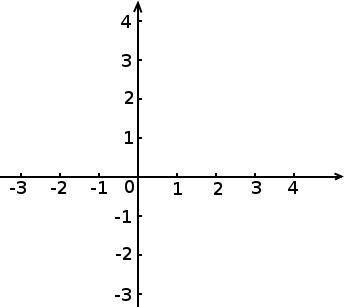
L’axe horizontal va alors représenter l’ensemble de départ et l’axe vertical celui d’arrivée. Si par exemple quand on prend le nombre 1 dans l’ensemble de départ, la fonction nous renvoie le nombre 3, nous allons représenter cela par un point qui se situe de la façon suivante :

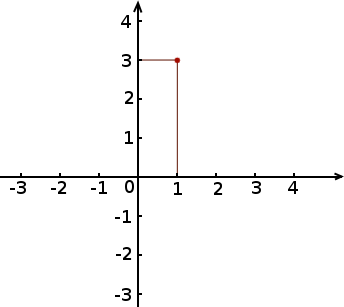
Le graphe de la fonction, c’est la figure que l’on obtient en plaçant tous les points obtenus pour tous les nombres de l’ensemble de départ.

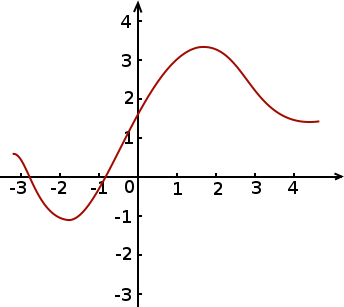
Pour les suites le fonctionnement est le même, mais il n’y a des points qu’au dessus des nombres entiers de l’axe horizontal.

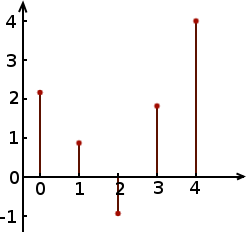
Pour plus de visibilité, puisqu’on a de la place, on peut carrément représenter cela avec des rectangles.

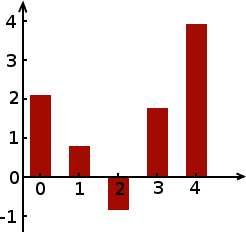
Le principe est tout simple, et pourtant, il n’est pas toujours facile de trouver le graphe d’une fonction à partir de sa formule. L’étude d’une fonction pour tracer son graphe fait parfois appel à des méthodes subtiles (voire franchement compliquées dans les pires des cas). Nous ne nous y attarderons pas ici, ce sujet pourrait faire l’objet d’un tuto à lui tout seul.

Nous avons vu dans le premier chapitre la définition la plus générale qui soit d’une fonction, mais cette définition a beaucoup évolué au cours de l’histoire. Dans cette section nous allons voir comment cette notion s’est transformée, ce qui va nous permettre de mettre le doigt sur quelques subtilités auxquelles on ne pense pas forcément quand on débute.

Le mot fonction a été introduit en 1692 par le mathématicien Gottfried Wilhelm Leibniz et provient du latin fuctio qui signifie exécution. Une fonction est donc un objet qui exécute une tâche. Pour Leibniz, il n’était pas encore question de prendre des ensembles de départ et d’arrivée quelconques : pour lui le terme ne désignait que les fonctions réelles. Les fonctions étaient étudiées à partir de leur graphe qui donnait des interprétations géométriques aux calculs effectués.

Au XVIIIe siècle, le terme est adopté par plusieurs mathématiciens parmi lesquels, le plus grand d’entre-eux, Leonhard Euler. Pour ce dernier, une fonction est une suite d’opérations que l’on fait subir à un nombre.

Aujourd’hui, comme nous l’avons vu dans le chapitre précédent, une fonction est tout simplement une machine qui pour chaque objet de son ensemble de définition en renvoie un autre dans l’ensemble d’arrivée, même s’il n’y a aucune logique particulière dans la façon dont les objets d’entrée et d’arrivée sont associés.

Pour bien saisir la différence entre la définition moderne et celle d’Euler, prenons deux exemples concrets :

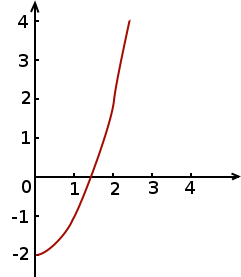
• Exemple 1. On considère une fonction qui à un nombre réel positif associe son carré moins deux.
• Exemple 2. On regarde le parcours d’un cycliste et on considère la fonction qui à chaque instant associe le nombre de kilomètres effectués.

Voici les graphes de ces deux fonctions :

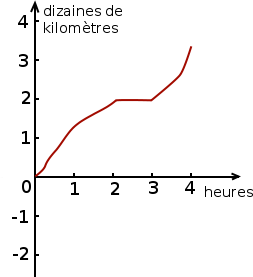Dans le premier exemple, la fonction est définie par une formule, on peut écrire $f(x)=x^2-2$. Pour le second, en revanche, il n’y a pas de formule : le cycliste peut rouler de façon très irrégulière, on ne peut pas trouver la distance parcourue à partir du temps par une simple formule.

Pour ces raisons, seul le premier exemple aurait été considéré comme une fonction par Euler au XVIIIe siècle.