Nous allons maintenant voir les circuits chargés de gérer la géométrie. Il existe deux grands types de circuits chargés de traiter la géométrie :
- l'input assembler ;
- et les circuits de traitement de vertices.
Input assembler
Avant leur traitement, les vertices sont stockées dans un tableau en mémoire vidéo : le vertex buffer. L'input assembler va charger les vertices dans les unités de traitement des vertices. Pour ce faire, il a besoin d'informations mémorisées dans des registres :
- l'adresse du vertex buffer en mémoire ;
- sa taille ;
- du type des données qu'on lui envoie (vertices codées sur 32 bits, 64, 128, etc).
L'input assembler peut aussi gérer des lectures simultanées dans plusieurs vertex buffers, si la mémoire vidéo le permet.
Triangles strip
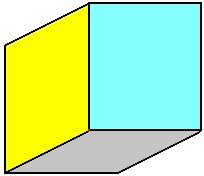
Il arrive qu'une vertice soit réutilisée dans plusieurs triangles. Par exemple, prenez le cube de l'image ci-dessous. Le sommet rouge du cube appartient aux 3 faces grise, jaune et bleue, et sera présent en trois exemplaires dans le vertex buffer : un pour la face bleue, un pour la jaune, et un pour la grise. Pour éviter ce gâchis, les concepteurs d'API et de cartes graphiques ont inventé des techniques pour limiter la consommation de mémoire.
La technique des triangles strip permet d'optimiser le rendu de triangles placés en série, qui ont une arête et deux sommets en commun.
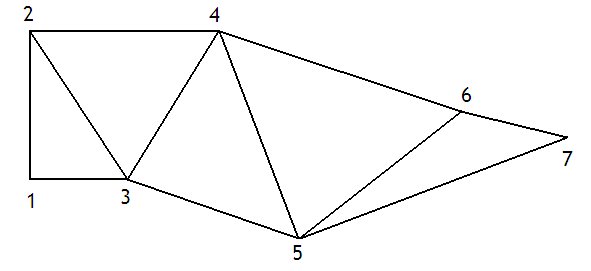
L'optimisation consiste à ne stocker complètement que le premier triangle le plus à gauche, les autres triangles étant codés avec une seule vertice. Cette vertice est combinée avec les deux dernières vertices chargées par l'input assembler pour former un triangle. Pour gérer ces triangles strips, l'input assembler doit mémoriser dans un registre les deux dernières vertices utilisées. En mémoire, le gain est énorme : au lieu de trois vertices pour chaque triangle, on se retrouve avec une vertice pour chaque triangle, sauf le premier de la surface.
Triangle fan
La technique des triangles fan fonctionne comme pour le triangles strip, sauf que la vertice n'est pas combinée avec les deux vertices précédentes. Supposons que je crée un premier triangle avec les vertices v1, v2, v3. Avec la technique des triangles strips, les deux vertices réutilisées auraient été les vertices v2 et v3. Avec les triangles fans, les vertices réutilisées sont les vertices v1 et v3. Les triangles fans sont utiles pour créer des figures comme des cercles, des halos de lumière, etc.
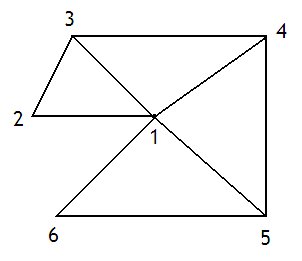
Index buffers
Enfin, nous arrivons à la dernière technique, qui permet de stocker chaque vertice en un seul exemplaire dans le vertex buffer. Le vertex buffer est couplé à un index buffer, un tableau d'indices qui servent à localiser la vertice dans le vertex buffer. Quand on voudra charger une vertice depuis la mémoire vidéo, il suffira de fournir l'indice de la vertice. Pour charger plusieurs fois la même vertice, il suffira de fournir le même indice à l'input assembler.
Dit comme cela, on ne voit pas vraiment où se trouve le gain en mémoire. On se retrouve avec deux tableaux : un pour les indices, un pour les vertices. Le truc, c'est qu'un indice prend beaucoup moins de place qu'une vertice. Un indice tient au grand maximum sur 32 bits, là où une vertice peut prendre 128 à 256 bits facilement. Entre copier 7 fois la même vertice, et avoir 7 indices et une vertice, le gain en mémoire est du côté de la solution à base d'index.
Vertex cache
Avec un index buffer, une vertice peut être chargée plusieurs fois depuis la mémoire vidéo. Pour exploiter cette propriété, les cartes graphiques intercalent une mémoire ultra-rapide entre la mémoire vidéo et la sortie de l'input assembler : le vertex cache. Lorsqu'une vertice est lue depuis la mémoire, elle est placée dans ce cache. Lors des utilisations ultérieures, la carte graphique lira la vertice depuis le cache, au lieu d'accéder à la mémoire vidéo, plus lente.
Cette mémoire est transparente via à vis de l'input assembler : les accès mémoire sont interceptés par la mémoire cache, qui vérifie si l'adresse demandée correspond à une donnée dans le vertex cache. Pour cela, chaque vertice est stockée dans la mémoire cache avec son indice : si jamais l'indice intercepté est présent dans le cache, le cache renvoie la vertice associée.
Sur les cartes graphiques assez anciennes, cette mémoire cache est souvent très petite : elle contient à peine 30 à à 50 vertices. Pour profiter le plus possible de ce vertex cache, les concepteurs de jeux vidéo peuvent changer l'ordre des vertices en mémoire : ainsi, l'ordre de lecture des vertices peut profiter de manière optimale du cache.
Transformation
Une fois la vertice chargée depuis la mémoire, elle est envoyée dans une unité chargée de la traiter. Chaque vertice appartient à un objet, dont la surface est modélisée sous la forme d'un ensemble de points. Chaque point est localisé par rapport au centre de l'objet qui a les coordonnées (0, 0, 0).
La première étape consiste à placer cet objet aux coordonnées (X, Y, Z) déterminées par le moteur physique : le centre de l'objet passe des coordonnées (0, 0, 0) aux coordonnées (X, Y, Z) et toutes les vertices de l'objet doivent être mises à jour. De plus, l'objet a une certaine orientation : il faut aussi le faire tourner. Enfin, l'objet peut aussi subir une mise à l'échelle : on peut le gonfler ou le faire rapetisser, du moment que cela ne modifie pas sa forme, mais simplement sa taille.
En clair, l'objet subit :
- une translation ;
- une rotation ;
- et une mise à l'échelle.
Ensuite, la carte graphique va effectuer un dernier changement de coordonnées. Au lieu de considérer un des bords de la scène 3D comme étant le point de coordonnées (0, 0, 0), il va passer dans le référentiel de la caméra. Après cette transformation, le point de coordonnées (0, 0, 0) sera la caméra. La direction de la vue du joueur sera alignée avec l'axe de la profondeur (l'axe Z).
Toutes ces transformations ne sont pas réalisées les unes après les autres. À la place, elles sont toutes effectuées en un seul passage. Pour réussir cet exploit, les concepteurs de cartes graphiques et de jeux vidéos utilisent ce qu'on appelle des matrices, des tableaux organisés en lignes et en colonnes avec un nombre dans chaque case. Le lien avec la 3D, c'est qu'appliquées sur le vecteur (X, Y, Z) des coordonnées d'une vertice, la multiplication par une matrice peut simuler des translations, des rotations, ou des mises à l'échelle.
Mais les matrices qui le permettent sont des matrices avec 4 lignes et 4 colonnes. Et pour multiplier une matrice par un vecteur, il faut que le nombre de coordonnées dans le vecteur soit égal au nombre de colonnes. Pour résoudre ce petit problème, on ajoute une 4éme coordonnée, la coordonnée homogène. Pour faire simple, elle ne sert à rien, et est souvent mise à 1, par défaut.
Il existe des matrices pour la translation, la mise à l'échelle, d'autres pour la rotation, etc. Et mieux : il existe des matrices dont le résultat correspond à plusieurs opérations simultanées : rotation ET translation, par exemple. Autant vous dire que le gain en terme de performances est assez sympathique.
Les anciennes cartes graphiques contenaient un circuit spécialisé dans ce genre de calculs, qui prenait une vertice et renvoyait la vertice transformée. Il était composé d'un gros paquet de multiplieurs et d'additionneurs flottants. Pour plus d'efficacité, certaines cartes graphiques comportaient plusieurs de ces circuits, afin de pouvoir traiter plusieurs vertices d'un même objet en même temps.
Eclairage
Seconde étape de traitement : l'éclairage. À la suite de cette étape d'éclairage, chaque vertice se voit attribuer une couleur, qui correspond à sa luminosité.
Données vertices
À partir de ces informations, la carte graphique va devoir calculer 4 couleurs, attribuées à chaque vertice. Chacune de ces couleurs est une couleur au format RGB. Ces 4 couleurs sont :
- la couleur diffuse ;
- la couleur spéculaire ;
- la couleur ambiante ;
- la couleur émissive.
La couleur ambiante correspond à la couleur réfléchie par la lumière ambiante. Par lumière ambiante, on parle de la lumière qui n'a pas vraiment de source de lumière précise, qui est égale en tout point de notre scène 3D (d’où le terme lumière ambiante). Par exemple, on peut simuler le soleil sans utiliser de source de lumière grâce à cette couleur.
La couleur diffuse vient du fait que la surface d'un objet diffuse une partie de la lumière qui lui arrive dessus dans toutes les directions. Cette lumière « rebondit » sur la surface de l'objet et une partie s'éparpille dans un peu toutes les directions.
Vient ensuite la couleur spéculaire, la couleur due à la lumière réfléchie par l'objet. Lorsqu'un rayon lumineux touche une surface, une bonne partie de celui-ci est réfléchie suivant un angle bien particulier (réflexion de Snell-Descartes). Suivant l'angle entre la source de lumière, la position de la caméra, son orientation, et la surface, une partie plus ou moins importante de cette lumière réfléchie sera renvoyée vers la caméra.
Et enfin, on trouve la couleur émissive : c'est la couleur de la lumière produite par l'objet. Il arrive que certains objets émettent de la lumière, sans pour autant être des sources de lumière.
La carte graphique a aussi besoin de l'angle avec lequel arrive un rayon lumineux sur la surface de l'objet. Pour gérer l'orientation de la surface, la vertice est fournie avec une information qui indique comment est orientée la surface : la normale. Cette normale est un simple vecteur, perpendiculaire à la surface de l'objet, dont l'origine est la vertice.
Autre paramètre d'une surface : sa brillance. Celle-ci indique si la surface brille beaucoup ou pas.
Calcul de l'éclairage
À partir de ces informations, la carte graphique calcule l'éclairage. Les anciennes cartes graphiques, entre la Geforce 256 et la Geforce FX contenaient des circuits câblés capables d'effectuer des calculs d'éclairage simples. Cette fonction de calcul de l'éclairage faisait partie intégrante d'un gros circuit nommé le T&L. Dans ce qui va suivre, nous allons voir l'algorithme d'éclairage de Phong, une version simplifiée de la méthode utilisée dans les circuits de T&L.
Tout d'abord, la couleur émissive ne change pas : elle ne subit aucun calcul.
Ensuite, la couleur ambiante de notre objet est multipliée par l'intensité de la lumière ambiante.
La couleur diffuse est calculée en multipliant :
- la couleur diffuse de la vertice ;
- l'intensité de la source de lumière ;
- et le cosinus entre la normale, et le rayon de lumière qui touche la vertice.
Ce cosinus sert à gérer l'orientation de la surface comparée à la source de lumière : plus le rayon de lumière incident rase la surface de l'objet, moins celui-ci diffusera de lumière.
Ensuite, la lumière réfléchie, spéculaire est calculée. Pour cela, il suffit de multiplier :
- la couleur spéculaire ;
- l'intensité de la source lumineuse ;
- et un paramètre qui dépend de la direction du regard de la caméra, et de la direction du rayon réfléchi par la surface.
Ce rayon réfléchi correspond simplement à la direction qu'aurait un rayon de lumière une fois réfléchi par la surface de notre objet. Pensez à la loi de Snell-Descartes. Le paramètre en question se calcule avec cette formule : cos^brillance (couleur_spéculaire).
Enfin, les 4 couleurs calculées plus haut sont additionnées ensemble. Chaque composante rouge, bleu, ou verte de la couleur sera traitée indépendamment des autres.