A ce stade, les vertices ont étés converties en triangles, après une éventuelle phase de tesselation. Mais toutes les vertices ne s'afficheront pas à l'écran : une bonne partie n'est pas dans le champ de vision, une autre est caché par d'autres objets, etc. Dans un souci d'optimisation, ces vertices non-visibles doivent être éliminées.
Une première optimisation consiste à ne pas afficher les triangles en-dehors du champ de vision de la caméra : c'est le clipping. Toutefois, un soin particulier doit être pris pour les triangles dont une partie seulement est dans le champ de vision : ceux-ci doivent être découpés en plusieurs triangles, tous présents intégralement dans le champ de vision.
La seconde s'appelle le Back-face Culling. Celle-ci va simplement éliminer les triangles qui tournent le dos à la caméra. Ces triangles sont ceux qui sont placés sur les faces arrière d'une surface. On peut déterminer si un triangle tourne le dos à la caméra en effectuant des calculs avec sa normale.
Triangle setup
Une fois tous les triangles non-visibles éliminés, la carte graphique va attribuer les triangles restants à des pixels : c'est l'étape de Triangle Setup.
Fonction de contours
On peut voir un triangle comme une portion du plan délimitée par trois droites. À partir de chaque droite, on peut créer une fonction de contours, qui va prendre un pixel et va indiquer de quel côté de la droite se situe le pixel. La fonction de contours va, pour chaque point sur l'image, renvoyer un nombre entier :
- si le point est placé sur la droite, la fonction renvoie zéro ;
- si le point est placé d'un coté de la droite, cette fonction renvoie un nombre négatif ;
- et enfin, si le point est placé de l'autre coté, la fonction renvoie un nombre positif.
Comment calculer cette fonction ? Tout d'abord, nous allons dire que le point que nous voulons tester a pour coordonnées x et y sur l'écran. Ensuite, nous allons prendre un des sommets du triangle, de coordonnées X et Y. L'autre sommet, placé sur cette droite, sera de coordonnées X2 et Y2. La fonction est alors égale à :
Si vous appliquez cette fonction sur chaque coté du triangle, vous allez voir une chose assez intéressante :
- à l'intérieur du triangle, les trois fonctions (une par côté) donneront un résultat positif ;
- à l'extérieur, une des trois fonctions donnera un résultat négatif.
Pour savoir si un pixel appartient à un triangle, il suffit de tester le résultat des fonctions de contours.
Triangle traversal
Dans sa version la plus naïve, tous les pixels de l'écran sont testés pour chaque triangle. Si le triangle est assez petit, une grande quantité de pixels seront testés inutilement. Pour éviter cela, diverses optimisations ont étés inventées.
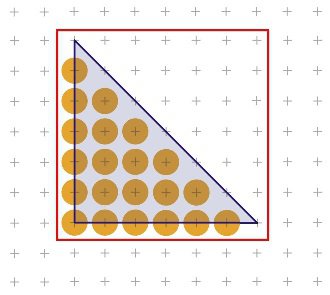
La première consiste à déterminer le plus petit rectangle possible qui contient le triangle, et à ne tester que les pixels de ce rectangle.
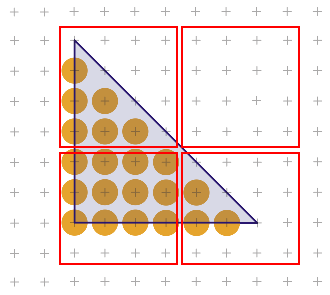
De nos jours, les cartes graphiques actuelles se basent sur une amélioration de cette méthode. Le principe consiste à prendre ce plus petit rectangle, et à le découper en morceaux carrés. Tous les pixels d'un carré seront testés simultanément, dans des circuits séparés, ce qui est plus rapide que les traiter uns par uns.
Interpolation des pixels
Une fois l'étape de triangle setup terminée, on sait donc quels sont les pixels situés à l'intérieur d'un triangle donné. Mais il faut aussi remplir l'intérieur des triangles : les pixels dans le triangle doivent être coloriés, avoir une coordonnée de profondeur, etc. Pour cela, nous sommes obligés d'extrapoler la couleur et la profondeur à partir des données situées aux sommets. Par exemple, si j'ai un sommet vert, un sommet rouge, et un sommet bleu, le triangle résultant doit être colorié comme ceci :

Cela va être fait par une étape d'interpolation, qui va calculer les informations à attribuer aux pixels qui ne sont pas pile-poil sur une vertice.
Fragments
Ce que l'étape de triangle setup va fournir, ce sont des informations qui précisent quelle est la couleur, la profondeur d'un pixel calculée à partir d'un triangle. Or, il est rare qu'on ne trouve qu'un seul triangle sur la trajectoire d'un pixel : c'est notamment le cas quand plusieurs objets sont l'un derrière l'autre. Si vous tracer une demi-droit dont l'origine est la caméra, et qui passe par le pixel, celle-ci intersecte la géométrie en plusieurs points : ces points sont appelés des fragments.
Dans la suite, les fragments attribués à un même pixel sont combinés pour obtenir la couleur finale de ce pixel. Mais cela s'effectuera assez loin dans le pipeline graphique, et nous reviendrons dessus en temps voulu.
Coordonnées barycentriques
Pour calculer les couleurs et coordonnées de chaque fragment, on va utiliser les coordonnées barycentriques. Pour faire simple, ces coordonnées sont trois coordonnées notées u, v et w. Pour les déterminer, nous allons devoir relier le fragment aux trois autres sommets du triangle, ce qui donne trois triangles :
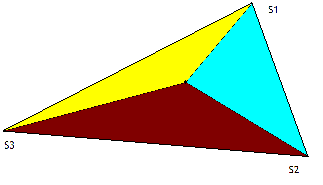
Les coordonnées barycentriques sont simplement proportionnelles aux aires de ces trois triangles. L'aire totale du triangle, ainsi que l'aire des trois sous-triangles, sont calculées par un petit calcul tout simple, que la carte graphique peut faire toute seule.
Quand je dis proportionnelles, il faut savoir que ces trois aires sont divisées par l'aire totale du triangle, qui se ramène dans l'intervalle [0, 1]. Cela signifie que la somme de ces trois coordonnées vaut 1 : u + v + w = 1. En conséquence, on peut se passer d'une des trois coordonnées dans nos calculs, vu que w = 1 - (u + v).
Perspective
Ces trois coordonnées permettent de faire l'interpolation directement . Il suffit de multiplier la couleur/profondeur d'un sommet par la coordonnée barycentrique associée, et de faire la somme de ces produits. Si l'on note C1, C2, et C3 les couleurs des trois sommets, la couleur d'un pixel vaut : (C1 * u) + (C2 * v) + (C3 * w).
Le résultat obtenu est alors celui du milieu :

Le problème : la perspective n'est pas prise en compte ! Intuitivement, on pouvait le deviner : la coordonnée de profondeur (z) n'était pas prise en compte dans le calcul de l’interpolation. Pour résumer, le problème vient du fait que l’interpolation de la cordonnée z est à l'origine de la mauvaise perspective : en interpolant 1/z, et en calculant z à partir de cette valeur interpolée, les problèmes disparaissent.