Can you multiply triples ?
Hamilton se lance donc dans la quête d’un système de nombres à 3 dimensions, de la forme :
avec et . Mais attention : n’est pas égal à . Par analogie avec les nombres complexes, est perpendiculaire à et à , ce qui donne la représentation géométrique suivante :
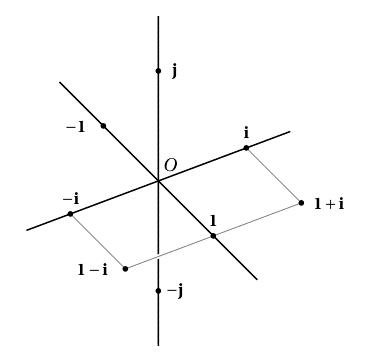
En ce qui concerne les opérations algébriques :
- L’addition de deux nombres ne lui pose aucune difficulté : elle se fait par addition des composants :
- Et la multiplication ? Si on utilise les lois normales de l’algèbre (associativité, commutativité et distributivité), on obtient :
Du coup, que vaut ? Pour que la multiplication donne un nombre à trois dimensions, doit être égal à un nombre de la forme . Mais toutes les tentatives d’Hamilton pour trouver les coefficients , et vont échouer. En effet, pour que ses nombres remplissent leur rôle géométrique, il faut que la multiplication obéisse à une autre règle : comme pour les nombres complexes, le produit des modules doit être égal au module du produit. Dit autrement, pour deux nombres et , on doit avoir : .
C’est cette règle qui empêchera Hamilton de créer une algèbre cohérente en trois dimensions, comme nous le montrerons tout à l’heure. Sa quête durera treize ans ! Comme il le raconte dans sa biographie, tous les matins, ses enfants lui demandaient :
- Papa, can you multiply triples ?
Ce à quoi il était obligé de répondre : - No, I can only add and substract them.
Jusqu’à ce fameux jour d’octobre 1843…
On a perdu la commutativité !
Alors qu’il fait sa promenade matinale, Hamilton a une illumination ! Il sort son couteau et grave sur le pont de Brougham la formule suivante :

Plaque commémorative sur le pont de Brougham
Cette formule semble défier les lois de l’algèbre. Et d’où sort ce ?
L’illumination qu’a Hamilton, c’est que le produit ne donne pas un nombre à 3 dimensions, mais un nombre qui se trouve dans une autre dimension, perpendiculaire à , à et à !
Il note ce nombre . Comme l’axe contenant est perpendiculaire à l’axe des réels, par analogie avec et , il pose .
De même, il pose et , ce qui donne .
Ce ne sont donc plus des nombres à 3 dimensions qu’il se met à étudier, mais des nombres à 4 dimensions : des quaternions, de la forme .
L’ensemble des nombres obtenu est appelé , l’ensemble des nombres hypercomplexes
Il lui reste cependant une dernière difficulté à surmonter. En effet, imaginons le calcul suivant :
par associativité de la multiplication
par commutativité de la multiplication
car
car
!!
Il lui faut résoudre ce problème très rapidement, sinon ses nouveaux nombres sont condamnés à disparaître aussi vite qu’ils sont apparus… Hamilton effectue alors un acte désespéré :
Pour lever ce paradoxe, Hamilton sacrifie une loi de l’algèbre : la commutativité de la multiplication.
Il pose , ainsi que et , ce qui résout le problème.
Le schéma suivant permet de se remémorer ces règles de calcul :
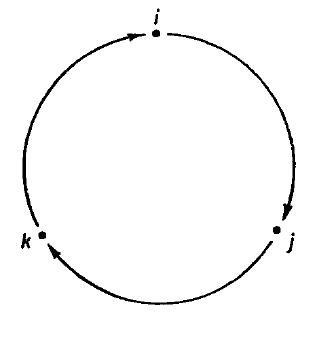
En parcourant le cercle dans le sens horaire, on retrouve les produits , et
En parcourant le cercle dans le sens contraire, on inverse les signes (, et )
Et là le miracle se produit : Hamilton obtient une algèbre cohérente (addition, soustraction, multiplication et division) et compatible avec la loi de multiplication des modules ().
La grosse nouveauté, c’est la perte de la commutativité ! Elle peut sembler choquante, et pourtant elle est bien compatible avec le rôle géométrique qu’on veut faire tenir à ces nouveaux nombres. En effet, rappelez-vous ce qui nous a conduit à les inventer : généraliser à la troisième dimension la géométrie des nombres complexes, notamment les rotations. Or, faites cette petite expérience chez vous : tendez votre poing gauche fermé devant vous, paume vers le bas.
- tournez votre poignet d’un quart de tour vers la gauche, puis d’un quart de tour vers l’avant : votre poing est maintenant dirigé vers le bas.
- tournez votre poignet d’un quart de tour vers l’avant, puis d’un quart de tour vers la gauche : votre poing est maintenant dirigé vers la droite.
Le résultat est différent selon l’ordre dans lequel on effectue les rotations !
Les rotations dans l’espace ne sont pas commutatives, tout comme la multiplication des quaternions !!