De quoi il s'agit
Ce tutoriel au sujet bien exotique va tenter d'explorer en partie un objet fascinant par sa simplicité et sa grande profondeur : la sphère $\mathbf{S}^2\subset \mathbf{R}^3$.
C'est un objet que l'on rencontre très facilement, et pourtant, on étudie assez peu les transformations régulières de cette sphère.
Nous tâcherons de donner des outils performants pour étudier $\mathbf{S}^2$. Nous utiliserons pour cela une identification avec la sphère de Riemann : $\hat{\mathbf{C}}= \mathbf{C}\cup \{\infty\}$. Les nombres complexes et les résultats analytiques les concernant seront centraux dans cette étude.
À qui s'adresse ce contenu ?
Ce contenu un peu plus poussé nécessite au préalable quelques connaissances en topologie et en analyse complexe. Même si les notions réutilisées seront rappelées, le lecteur devra être suffisamment à l'aise avec pour les aborder.
Outils d'analyse complexe
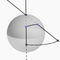
Projection stéréographique et compactification
- Identification de $\mathbf{S}^2$ à $\hat{\mathbf{C}}$
- La compactification de $\mathbf{C}$ en $\hat{\mathbf{C}}$
Fonctions holomorphes sur la sphère
Ouverture
Tout ceci ne s'arrête pas là. La sphère de Riemann est également identifiable à un autre objet algébrique très riche : la droite projective complexe, notée $\mathbf{C}\mathbf{P}^1$ ou $\mathbf{P}(\mathbf{C}^2)$. C'est alors encore une nouvelle source de résultats fondamentaux et simples. On peut par exemple montrer qu'il existe un unique isomorphisme qui échange deux triplets.
On peut également s'intéresser à la sphère $\mathbf{S}^2$ du point de vue de la topologie différentielle. La considérer comme une variété différentielle, chez les réels cette fois-ci, et en déduire des résultats également très variés. On peut de cette manière montrer le très célèbre théorème de d'Alembert-Gauss, par des outils de topologie différentielle très simples et sans recours à de l'analyse complexe.
Références
Pour des références en topologie générale et analyse complexe, le lecteur peu à l'aise avec ces notions peu se rediriger vers les polycopiés (très complets) suivants :
- Topologie général et calcul différentiel de F. Paulin ;
- Analyse complexe de M. Audin.
En guise d'approfondissements, le lecteur intéressé peut se diriger vers les livres suivants :
- Complex Functions de Jones et Singerman
- Dynamics in One Complex Variable de Milnor





 )
)
