ACSL - Définitions logiques et code fantôme

Les prédicats inductifs donnent une manière d’énoncer des propriétés dont la vérification nécessite de raisonner par induction, c’est-à-dire que pour une propriété $p(input)$, on peut assurer qu’elle est vraie, soit parce qu’elle correspond à un certain cas de base (par exemple, $0$ est un entier naturel pair parce que l’on définit le cas 0 comme un cas de base), ou alors parce que sachant que $p$ est vraie pour un certain $smaller input$ (qui est « plus proche » du cas de base) et sachant que $smaller input$ et $input$ sont reliés par une propriété donnée (qui dépend de notre définition) nous pouvons conclure (par exemple nous pouvons définir que si un naturel $n$ est pair, le naturel $n+2$ est pair, donc pour vérifier qu’un naturel supérieur à 0 est pair, on peut regarder si ce naturel moins 2 est pair).

Syntaxe

Pour le moment, introduisons la syntaxe des prédicats inductifs :

/*@
  inductive property{ Label0, ..., LabelN }(type0 a0, ..., typeN aN) {
  case c_1{Lq_0, ..., Lq_X}: p_1 ;
  ...
  case c_m{Lr_0, ..., Lr_Y}: p_km ;
  }
*/

où tous les c_i sont des noms et tous les p_i sont des formules logiques où property apparaît en conclusion. Pour résumer, property est vraie pour certains paramètres et labels mémoire, s’ils valident l’un des cas du prédicat inductif.

Jetons un œil à la petite propriété dont nous parlions plus tôt : comment définir qu’un entier naturel est pair par induction ? Nous pouvons traduire la phrase : « 0 est un naturel pair, et si $n$ est un naturel pair, alors $n+2$ est aussi un naturel pair ».

/*@
  inductive even_natural{L}(integer n) {
  case even_nul{L}:
    even_natural(0);
  case even_not_nul_natural{L}:
    \forall integer n ; 
      even_natural(n) ==> even_natural(n+2);
  }
*/

Ce prédicat définit bien les deux cas :

• $0$ est un naturel pair (case de base),
• si un naturel $n$ est pair, $n+2$ est pair aussi (induction).

Cependant, cette définition n’est pas complètement satisfaisante. Par exemple, nous ne pouvons pas déduire qu’un naturel impair n’est pas pair. Si nous essayons de prouver que $1$ est pair, nous devons vérifier que si $-1$ est pair, puis $-3$, $-5$, etc. De plus, nous préférons généralement indiquer la condition selon laquelle une conclusion donnée est vraie en utilisant les variables quantifiées dans la conclusion. Par exemple, ici, pour montrer qu’un entier $n$ est naturel, comment faire ? D’abord vérifier s’il est égal à 0, et si ce n’est pas le cas, vérifier qu’il est plus grand que 0, et dans ce cas, vérifier que $n-2$ est pair :

/*@
  inductive even_natural{L}(integer n) {
  case even_nul{L}:
    even_natural(0) ;
  case even_not_nul_natural{L}:
    \forall integer n ; n > 0 ==> even_natural(n-2) ==>
      even_natural(n) ;
  }
*/

Ici nous distinguons à nouveau deux cas :

• 0 est pair,
• un naturel $n$ est pair s’il est plus grand que $0$ et $n-2$ est un naturel pair.

Pour un entier naturel donné, s’il est plus grand que 0, nous diminuerons récursivement sa valeur jusqu’à atteindre 0 ou -1. Dans le cas 0, l’entier naturel est pair. Dans le cas -1, nous n’aurons aucun cas du prédicat inductif qui corresponde à cette valeur et nous pourrons conclure que la propriété est fausse (même si nous verrons plus tard que nous avons besoin d’un assistant de preuve pour arriver cette conclusion dans le cas de WP).

void foo(){
  int a = 42 ;
  //@ assert even_natural(a);
}

Bien sûr, définir la notion d’entier naturel pair par induction n’est pas une bonne idée, un modulo serait plus simple. Nous utilisons généralement les propriétés inductives pour définir des propriétés récursives complexes.

Consistance

Les définitions inductives apportent le risque d’introduire des inconsistances. En effet, les propriétés spécifiées dans les différents cas sont considérées comme étant toujours vraies, donc si nous introduisons des propriétés permettant de prouver false, nous sommes en mesure de prouver n’importe quoi. Même si nous parlerons plus longuement des axiomes dans la section à propos des définitions axiomatiques, nous pouvons donner quelques conseils pour ne pas construire une mauvaise définition.

D’abord, nous pouvons nous assurer que les prédicats inductifs sont bien fondés. Cela peut être fait en restreignant syntaxiquement ce que nous acceptons dans une définition inductive en nous assurant que chaque cas est de la forme :

/*@
  \forall y1,...,ym ; h1 ==> ··· ==> hl ==> P(t1,...,tn) ;
*/

où le prédicat P ne peut apparaître que positivement (donc sans la négation ! - $\neg$) dans les différentes hypothèses hx. Intuitivement, cela assure que nous ne pouvons pas construire des occurrences à la fois positives et négatives de P pour un ensemble de paramètres donnés (ce qui serait incohérent).

Cette propriété est par exemple vérifiée pour notre définition précédente du prédicat even_natural. Tandis qu’une définition comme :

/*@
  inductive even_natural{L}(integer n) {
  case even_nul{L}:
    even_natural(0) ;
  case even_not_nul_natural{L}:
    \forall integer n ; n > 0 ==> even_natural(n-2) ==>
    // negative occurrence of even_natural
    !even_natural(n-1) ==> 
      even_natural(n) ;
  }
*/

ne respecte pas cette contrainte, car la propriété even_natural apparaît négativement à la ligne 8.

Ensuite, nous pouvons simplement écrire une fonction dont le contrat nécessite P. Par exemple, nous pouvons écrire la fonction suivante :

/*@
  requires P( params ... ) ;
  ensures  BAD: \false ;
*/ void function(params){

}

Pour notre définition de even_natural, cela donnerait :

/*@
  requires even_natural(n) ;
  ensures  \false ;
*/ void function(int n){

}

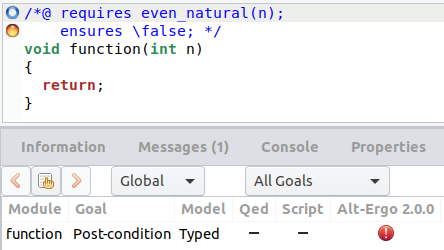
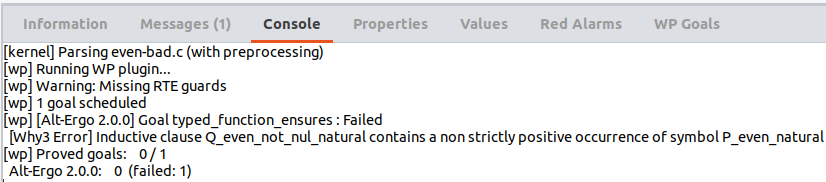
Pendant la génération de l’obligation de preuve, WP demande à Why3 de créer une définition inductive pour celle que nous avons écrit en ACSL. Comme Why3 est plus strict que Frama-C et WP pour ce type de définition, si le prédicat inductif est trop étrange (s’il n’est pas bien fondé), il sera rejeté avec une erreur. Et en effet, pour la propriété even_natural que nous venons de définir, Why3 la refuse quand nous tentons de prouver ensures \false, parce qu’il existe une occurrence non positive de P_even_natural qui encode le even_natural que nous avons écrit en ACSL.

frama-c-gui -wp -wp-prop=BAD file.c

Cependant, cela ne signifie pas que nous ne pouvons pas écrire une définition inductive inconsistante. Par exemple, la définition inductive suivante est bien fondée mais nous permet de prouver faux :

/*@ inductive P(int* p){
      case c: \forall int* p ; \valid(p) && p == (void*)0 ==> P(p);
    }
*/

/*@ requires P(p);
    ensures \false ; */
void foo(int *p){}

Ici nous pourrions détecter le problème avec -wp-smoke-tests qui trouverait que la précondition ne peut pas être satisfaite. Mais nous devons être prudents pendant la conception d’une définition inductive afin de ne pas introduire une définition qui nous permette de produire une preuve de faux.

Définitions de prédicats récursifs

Les prédicats inductifs sont souvent utiles pour exprimer des propriétés récursivement, car ils permettent souvent d’empêcher les solveurs SMT de dérouler la récursion quand c’est possible.

Par exemple, nous pouvons définir qu’un tableau ne contient que des zéros de cette façon :

/*@
  inductive zeroed{L}(int* a, integer b, integer e){
  case zeroed_empty{L}:
    \forall int* a, integer b, e; b >= e ==> zeroed{L}(a,b,e);
  case zeroed_range{L}:
    \forall int* a, integer b, e; b < e ==>
      zeroed{L}(a,b,e-1) && a[e-1] == 0 ==> zeroed{L}(a,b,e);
  }
*/

et nous pouvons à nouveau prouver notre fonction de remise à zéro avec cette nouvelle définition :

/*@
  requires \valid(array + (0 .. length-1));
  assigns  array[0 .. length-1];
  ensures  zeroed(array,0,length);
*/
void reset(int* array, size_t length){
  /*@
    loop invariant 0 <= i <= length;
    loop invariant zeroed(array,0,i);
    loop assigns i, array[0 .. length-1];
    loop variant length-i;
  */
  for(size_t i = 0; i < length; ++i)
    array[i] = 0;
}

Selon votre version de Frama-C et de vos prouveurs automatiques, la preuve de préservation de l’invariant peut échouer. Une raison à cela est que le prouveur ne parvient pas à garder l’information que ce qui précède la cellule en cours de traitement par la boucle est toujours à 0. Nous pouvons ajouter un lemme dans notre base de connaissance, expliquant que si l’ensemble des valeurs d’un tableau n’a pas changé, alors la propriété est toujours vérifiée :

/*@
  predicate same_elems{L1,L2}(int* a, integer b, integer e) =
    \forall integer i; b <= i < e ==> \at(a[i],L1) == \at(a[i],L2);
  lemma no_changes{L1,L2}:
    \forall int* a, integer b, e;
      same_elems{L1,L2}(a,b,e) ==> zeroed{L1}(a,b,e) ==> zeroed{L2}(a,b,e);
*/

et d’énoncer une assertion pour spécifier ce qui n’a pas changé entre le début du bloc de la boucle (marqué par le label L dans le code) et la fin (qui se trouve être Here puisque nous posons notre assertion à la fin) :

for(size_t i = 0; i < length; ++i){
  L:
    array[i] = 0;
    //@ assert same_elems{L,Here}(array,0,i);
}

À noter que dans cette nouvelle version du code, la propriété énoncée par notre lemme n’est pas prouvée par les solveurs automatiques, qui ne savent pas raisonner par induction. Pour les curieux, la (très simple) preuve en Coq est disponible ici :

(* Generated by Frama-C WP *)

Goal typed_lemma_no_changes.
Hint no_changes,property.
Proof.
  (* introduction des variables *)
  intros b e Mi Mi' arr H.
  (* on travaille par induction sur le prédicat*)
  induction H ; intros Same.
  + (* cas de base: trivial *)
    constructor 1 ; auto.
  + (* cas d'induction *)
    unfold x in * ; clear x.
    constructor 2 ; try omega.
    - (* on montre d'abord que l'élément ajouté est le même *)
      rewrite <- H ; symmetry.
      apply Same ; omega.
    - (* puis on montre que c'est vrai pour le reste par induction *)
      apply IHP_zeroed.
      intros i' ; intros.
      apply Same ; omega.
Qed.

Dans le cas présent, utiliser une définition inductive est contre-productif : notre propriété est très facilement exprimable en logique du premier ordre comme nous l’avons déjà fait précédemment. Nous utilisons généralement les prédicats inductifs lorsqu’il n’est pas si facile de travailler avec les constructions de base d’ACSL. Passons donc à un exemple plus complexe.

Exemple : le tri

Nous allons prouver un simple tri par sélection :

size_t min_idx_in(int* a, size_t beg, size_t end){
  size_t min_i = beg;
  for(size_t i = beg+1; i < end; ++i)
    if(a[i] < a[min_i]) min_i = i;
  return min_i;
}

void swap(int* p, int* q){
  int tmp = *p; *p = *q; *q = tmp;
}

void sort(int* a, size_t beg, size_t end){
  for(size_t i = beg ; i < end ; ++i){
    size_t imin = min_idx_in(a, i, end);
    swap(&a[i], &a[imin]);
  }
}

Le lecteur pourra s’exercer en spécifiant et en prouvant les fonctions de recherche de minimum et d’échange de valeur. Nous cachons la correction et nous nous concentrerons plutôt sur la spécification et la preuve de la fonction de tri qui sont une illustration intéressante de l’usage des définitions inductives.

/*@
  requires \valid_read(a + (beg .. end-1));
  requires beg < end;
  assigns  \nothing;
  ensures  \forall integer i; beg <= i < end ==> a[\result] <= a[i];
  ensures  beg <= \result < end;
*/
size_t min_idx_in(int* a, size_t beg, size_t end){
  size_t min_i = beg;

  /*@
    loop invariant beg <= min_i < i <= end;
    loop invariant \forall integer j; beg <= j < i ==> a[min_i] <= a[j];
    loop assigns min_i, i;
    loop variant end-i;
  */
  for(size_t i = beg+1; i < end; ++i){
    if(a[i] < a[min_i]) min_i = i;
  }
  return min_i;
}

/*@
  requires \valid(p) && \valid(q);
  assigns  *p, *q;
  ensures  *p == \old(*q) && *q == \old(*p);
*/
void swap(int* p, int* q){
  int tmp = *p; *p = *q; *q = tmp;
}

En effet, une erreur commune que nous pourrions faire dans le cas de la preuve du tri est de poser cette spécification (qui est vraie !) :

/*@
  predicate sorted(int* a, integer b, integer e) =
    \forall integer i, j; b <= i <= j < e ==> a[i] <= a[j];
*/

/*@
  requires \valid(a + (beg .. end-1));
  requires beg < end;
  assigns  a[beg .. end-1];
  ensures sorted(a, beg, end);
*/
void sort(int* a, size_t beg, size_t end){
  /* @ // add invariant */
  for(size_t i = beg ; i < end ; ++i){
    size_t imin = min_idx_in(a, i, end);
    swap(&a[i], &a[imin]);
  }
}

Cette spécification est correcte. Mais si nous nous rappelons la partie concernant les spécifications, nous nous devons d’exprimer précisément ce que nous attendons. Avec la spécification actuelle, nous ne prouvons pas toutes les propriétés nécessaires d’un tri ! Par exemple, cette fonction remplit pleinement la spécification :

/*@
  requires \valid(a + (beg .. end-1));
  requires beg < end;
  assigns  a[beg .. end-1];
  
  ensures sorted(a, beg, end);
*/
void fail_sort(int* a, size_t beg, size_t end){
  /*@
    loop invariant beg <= i <= end;
    loop invariant \forall integer j; beg <= j < i ==> a[j] == 0;
    loop assigns i, a[beg .. end-1];
    loop variant end-i;
  */
  for(size_t i = beg ; i < end ; ++i)
    a[i] = 0;
}

En fait, notre spécification oublie que tous les éléments qui étaient originellement présents dans le tableau à l’appel de la fonction doivent toujours être présents après l’exécution de notre fonction de tri. Dit autrement, notre fonction doit en fait produire la permutation triée des valeurs du tableau.

Une propriété comme la définition de ce qu’est une permutation s’exprime extrêmement bien par l’utilisation d’une définition inductive. En effet, pour déterminer qu’un tableau est la permutation d’un autre, les cas sont très limités. Premièrement, le tableau est une permutation de lui-même, puis l’échange de deux valeurs sans changer les autres est également une permutation, et finalement si nous créons la permutation $p_2$ d’une permutation $p_1$, puis que nous créons la permutation $p_3$ de $p_2$, alors par transitivité $p_3$ est une permutation de $p_1$.

La définition inductive correspondante est la suivante :

/*@
  predicate swap_in_array{L1,L2}(int* a, integer b, integer e, integer i, integer j) =
    b <= i < e && b <= j < e &&
    \at(a[i], L1) == \at(a[j], L2) &&
    \at(a[j], L1) == \at(a[i], L2) &&
    \forall integer k; b <= k < e && k != j && k != i ==>
      \at(a[k], L1) == \at(a[k], L2);
  inductive permutation{L1,L2}(int* a, integer b, integer e){
  case reflexive{L1}: 
    \forall int* a, integer b,e ; permutation{L1,L1}(a, b, e);
  case swap{L1,L2}:
    \forall int* a, integer b,e,i,j ;
      swap_in_array{L1,L2}(a,b,e,i,j) ==> permutation{L1,L2}(a, b, e);
  case transitive{L1,L2,L3}:
    \forall int* a, integer b,e ; 
      permutation{L1,L2}(a, b, e) && permutation{L2,L3}(a, b, e) ==> 
        permutation{L1,L3}(a, b, e);
  }
*/

Nous spécifions alors que notre tri nous crée la permutation triée du tableau d’origine et nous pouvons prouver l’ensemble en complétant l’invariant de la fonction :

/*@
  requires beg < end && \valid(a + (beg .. end-1));
  assigns  a[beg .. end-1];  
  ensures sorted(a, beg, end);
  ensures permutation{Pre, Post}(a,beg,end);
*/
void sort(int* a, size_t beg, size_t end){
  /*@
    loop invariant beg <= i <= end;
    loop invariant sorted(a, beg, i) && permutation{Pre, Here}(a, beg, end);
    loop invariant \forall integer j,k; beg <= j < i ==> i <= k < end ==> a[j] <= a[k];
    loop assigns i, a[beg .. end-1];
    loop variant end-i;
  */
  for(size_t i = beg ; i < end ; ++i){
    //@ ghost begin: ;
    size_t imin = min_idx_in(a, i, end);
    swap(&a[i], &a[imin]);
    //@ assert swap_in_array{begin,Here}(a,beg,end,i,imin);
  }
}

Cette fois, notre propriété est précisément définie, la preuve reste assez simple à faire passer, ne nécessitant que l’ajout d’une assertion que le bloc de la fonction n’effectue qu’un échange des valeurs dans le tableau (et donnant ainsi la transition vers la permutation suivante du tableau). Pour définir cette notion d’échange, nous utilisons une annotation particulière (à la ligne 16), introduite par le mot-clé ghost. Ici, le but est d’introduire un label fictif dans le code qui est uniquement visible d’un point de vue spécification. C’est l’objet de la section finale de ce chapitre, parlons d’abord des définitions axiomatiques.

Exercices

La somme des N premiers entiers

Reprendre la solution de l’exercice de la section sur les lemmes à propos de la somme des N premiers entiers. Réécrire la fonction logique en utilisant plutôt un prédicat inductif qui exprime l’égalité entre un entier et la somme des N premiers entiers.

#include <limits.h>

/*@
  inductive is_sum_n(integer n, integer res) {
    // ...
  }
*/

/*@ 
  requires n*(n+1) <= 2*INT_MAX ;
  assigns \nothing ;
  // ensures ... ; 
*/
int sum_n(int n){
  if(n < 1) return 0 ;

  int res = 0 ;
  /*@
    loop invariant 1 <= i <= n+1 ;
    // loop invariant ... ; 
    loop assigns i, res ;
    loop variant n - i ;
  */
  for(int i = 1 ; i <= n ; i++){
    res += i ;
  }
  return res ;
}

Adapter le contrat de la fonction et le(s) lemme(s). Notons que les lemmes ne seront certainement pas prouvés par les solveurs SMT. Nous fournissons une solution et les preuves Coq sur le GitHub de ce tutoriel.

Plus grand diviseur commun

Écrire un prédicat inductif qui exprime qu’un entier est le plus grand diviseur commun de deux autres. Le but de cet exercice est de prouver que la fonction gcd calcule le plus grand diviseur commun. Nous n’avons donc pas à spécifier tous les cas du prédicat. En effet, si nous regardons de près la boucle, nous pouvons voir qu’après la première itération, a est supérieur ou égal à b, et que cette propriété est maintenue par la boucle. Donc, considérons deux cas pour le prédicat inductif :

• b est 0,
• si une valeur d est le PGCD de b et a % b, alors c’est le PGCD de a et b.

#include <limits.h>

/*@ inductive is_gcd(integer a, integer b, integer div) {
    case gcd_zero: // ...
    case gcd_succ: // ...
    }
*/

/*@
  requires a >= 0 && b >= 0 ;
  assigns \nothing ;
  // ensures ... ;
*/
int gcd(int a, int b){
  /*@
    // loop invariant \forall integer t ; ... ;
  */ 
  while (b != 0){
    int t = b;
    b = a % b;
    a = t;
  }
  return a;
}

Exprimer la postcondition de la fonction et compléter l’invariant pour prouver qu’elle est vérifiée. Notons que l’invariant devrait utiliser le cas inductif gcd_succ.

Puissance

Dans cet exercice, nous ne considérerons pas les RTE.

Écrire un prédicat inductif qui exprime qu’un entier r est égal à $x^n$. Considérer deux cas : soit $n$ est 0, soit il est plus grand et à ce moment-là, la valeur de r est reliée à la valeur $x^{n-1}$.

/*@
  inductive is_power(integer x, integer n, integer r) {
  case zero: // ...
  case N: // ...
  }
*/

Prouver d’abord la version naïve de la fonction puissance :

/*@
  requires n >= 0 ;
  // assigns ...
  // ensures ...
*/
int power(int x, int n){
  int r = 1 ;
  /*@
    loop invariant 1 <= i <= n+1 ;
    // loop invariant ...
  */
  for(int i = 1 ; i <= n ; ++i){
    r *= x ;
  }  
  return r ;
}

Maintenant, tentons de prouver une version plus rapide de la fonction puissance :

/*@
  requires n >= 0 ;
  // assigns ...
  // ensures ...
*/
int fast_power(int x, int n){
  int r = 1 ;
  int p = x ;
  /*@
    loop invariant \forall integer v ; // ...
  */
  while(n > 0){
    if(n % 2 == 1) r = r * p ;
    p *= p ;
    n /= 2 ;
  }
  //@ assert is_power(p, n, 1) ;
  
  return r ;
}

Dans cette version, nous exploitons deux propriétés de l’opérateur puissance :

• $(x^2)^n = x^{2n}$
• $x \times (x^2)^n = x^{2n+1}$

qui permet de diviser $n$ par 2 à chaque tour de boucle au lieu de le décrémenter de un (ce qui permet à l’algorithme d’être en $O(\log n)$ et pas $O(n)$). Exprimer les deux propriétés précédentes sous forme de lemmes :

/*@
  lemma power_even: ...
  lemma power_odd: ...
*/

Exprimer d’abord le lemme power_even, les solveurs SMT pourraient être capables de combiner ce lemme avec la définition inductive pour déduire power_odd. La preuve Coq de power_even est fournie sur le GitHub de ce tutoriel ainsi que la preuve de power_odd si les solveurs SMT échouent.

Finalement, compléter le contrat et l’invariant de la fonction fast_power. Pour cela, notons qu’au début de la boucle $x^{old(n)} = p^n$, et que chaque itération utilise les propriétés précédentes pour mettre à jour $r$, au sens que nous avons $x^{old(n)} = r \times p^n$ pendant toute la boucle, jusqu’à obtenir $n = 0$ et donc $p^n = 1$.

Permutation

Reprendre la définition des prédicats shifted et unchanged de l’exercice sur la transitivité de shift dans la section sur les lemmes. Le prédicate shifted_cell peut être inliné et supprimé. Utiliser le prédicat shifted pour exprimer le prédicat rotate qui exprime que les éléments d’un tableau sont « tournés »  vers la gauche, dans le sens où tous les éléments sont glissés vers la gauche, sauf le dernier qui est mis à la première cellule de la plage de valeur. Utiliser ce prédicat pour prouver la fonction rotate.

/*@
  predicate rotate{L1, L2}(int* arr, integer fst, integer last) =
    // ...
*/

/*@
  assigns arr[beg .. end-1] ;
  ensures rotate{Pre, Post}(arr, beg, end) ;
*/
void rotate(int* arr, size_t beg, size_t end){
  int last = arr[end-1] ;
  for(size_t i = end-1 ; i > beg ; --i){
    arr[i] = arr[i-1] ;
  }
  arr[beg] = last ;
}

Exprimer une nouvelle version de la notion de permutation avec un prédicat inductif qui considère les cas suivants :

• la permutation est réflexive ;
• si la partie gauche d’une plage de valeur (jusqu’à un certain indice) est « tournée » entre deux labels, nous avons toujours une permutation ;
• si la partie droite d’une plage de valeur (à partir d’un certain indice) est « tournée » entre deux labels, nous avons toujours une permutation ;
• la permutation est transitive.

/*@
  inductive permutation{L1, L2}(int* arr, integer fst, integer last){
  case reflexive{L1}: // ...
  case rotate_left{L1,L2}: // ...
  case rotate_right{L1,L2}: // ...
  case transitive{L1,L2,L3}: // ...
  }
*/

Compléter le contrat de la fonction two_rotates qui fait des rotations successives, de la première et la seconde moitié de la plage considérée, et prouver qu’elle maintient la permutation.

void two_rotates(int* arr, size_t beg, size_t end){
  rotate(arr, beg, beg+(end-beg)/2) ;
  //@ assert permutation{Pre, Here}(arr, beg, end) ;
  rotate(arr, beg+(end-beg)/2, end) ;
}

Les axiomes sont des propriétés dont nous énonçons qu’elles sont vraies quelle que soit la situation. C’est un moyen très pratique d’énoncer des notions complexes qui pourront rendre le processus très efficace en abstrayant justement cette complexité. Évidemment, comme toute propriété exprimée comme un axiome est supposée vraie, il faut également faire très attention à ce que nous définissons, car si nous introduisons une propriété fausse dans les notions que nous supposons vraies alors … nous saurons tout prouver, même ce qui est faux.

Syntaxe

Pour introduire une définition axiomatique, nous utilisons la syntaxe suivante :

/*@
  axiomatic Name_of_the_axiomatic_definition {
    // ici nous pouvons définir ou déclarer des fonctions et prédicats

    axiom axiom_name { Label0, ..., LabelN }:
      // property ;

    axiom other_axiom_name { Label0, ..., LabelM }:
      // property ;

    // ... nous pouvons en mettre autant que nous voulons
  }
*/

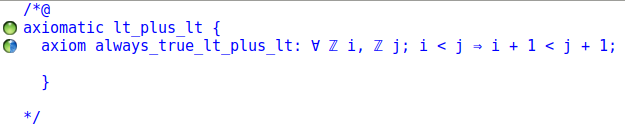
Nous pouvons par exemple définir cette axiomatique :

/*@
  axiomatic lt_plus_lt{
    axiom always_true_lt_plus_lt:
      \forall integer i, j; i < j ==> i+1 < j+1 ;
  }
*/

et nous pouvons voir que dans Frama-C, la propriété est bien supposée vraie :

/*@
  axiomatic Ax_answer_to_the_ultimate_question_of_life_the_universe_and_everything {
    logic integer the_ultimate_question_of_life_the_universe_and_everything{L} ;

    axiom answer{L}:
      the_ultimate_question_of_life_the_universe_and_everything{L} = 42;
  }
*/

Lien avec la notion de lemme

Les lemmes et les axiomes permettront d’exprimer les mêmes types de propriétés, à savoir des propriétés exprimées sur des variables quantifiées (et éventuellement des variables globales, mais cela reste assez rare puisqu’il est difficile de trouver une propriété qui soit globalement vraie à leur sujet tout en étant intéressante). Outre ce point commun, il faut également savoir que comme les axiomes, en dehors de leur définition, les lemmes sont considérés vrais par WP.

La seule différence entre lemme et axiome du point de vue de la preuve est donc que nous devrons fournir une preuve que le premier est valide alors que l’axiome est toujours supposé vrai.

Définition de fonctions ou prédicats récursifs

Les définitions axiomatiques de fonctions ou de prédicats récursifs sont particulièrement utiles, car elles permettent d’empêcher les prouveurs de dérouler la récursion quand c’est possible.

L’idée est alors de ne pas définir directement la fonction ou le prédicat mais plutôt de la déclarer puis de définir des axiomes spécifiant son comportement. Si nous reprenons par exemple la factorielle, nous pouvons la définir axiomatiquement de cette manière :

/*@
  axiomatic Factorial{
    logic integer factorial(integer n);
    
    axiom factorial_0:
      \forall integer i; i <= 0 ==> 1 == factorial(i) ;

    axiom factorial_n:
      \forall integer i; i > 0 ==> i * factorial(i-1) == factorial(i) ;
  }
*/

Dans cette définition axiomatique, notre fonction n’a pas de corps, son comportement étant défini par les axiomes ensuite définis. Excepté ceci, rien ne change, en particulier, notre fonction peut être utilisée dans nos spécifications, exactement comme avant.

Une petite subtilité est qu’il faut prendre garde au fait que si les axiomes énoncent des propriétés à propos du contenu d’une ou plusieurs zones mémoires pointées, il faut spécifier ces zones mémoires en utilisant la notation reads au niveau de la déclaration. Si nous oublions une telle spécification, le prédicat, ou la fonction, sera considéré comme énoncé à propos du pointeur et non à propos de la zone mémoire pointée. Une modification de celle-ci n’entraînera donc pas l’invalidation d’une propriété connue axiomatiquement.

Par exemple, si nous prenons la définition inductive que nous avons rédigée pour zeroed dans le chapitre précédent, nous pouvons l’écrire à l’aide d’une définition axiomatique qui prendra cette forme :

/*@
  axiomatic A_all_zeros{
    predicate zeroed{L}(int* a, integer b, integer e) reads a[b .. e-1];

    axiom zeroed_empty{L}:
      \forall int* a, integer b, e; b >= e ==> zeroed{L}(a,b,e);
      
    axiom zeroed_range{L}:
      \forall int* a, integer b, e; b < e ==>
        zeroed{L}(a,b,e-1) && a[e-1] == 0 <==> zeroed{L}(a,b,e);
  }
*/

Notons le reads[b .. e-1] qui spécifie la position mémoire dont le prédicat dépend. Tandis que nous n’avons pas besoin de spécifier les positions mémoires « lues » par une définition inductive, nous devons spécifier ces propriétés pour les propriétés définies axiomatiquement.

Consistance

En ajoutant des axiomes à notre base de connaissances, nous pouvons produire des preuves plus complexes car certaines parties de cette preuve, mentionnées par les axiomes, ne nécessiteront plus de preuves qui allongeraient le processus complet. Seulement, en faisant cela nous devons être extrêmement prudents. En effet, la moindre hypothèse fausse introduite dans la base pourraient rendre tous nos raisonnements futiles. Notre raisonnement serait toujours correct, mais basé sur des connaissances fausses, il ne nous apprendrait donc plus rien de correct.

L’exemple le plus simple à produire est le suivant:

/*@
  axiomatic False{
    axiom false_is_true: \false;
  }
*/

int main(){
  // Exemples de propriétés prouvées

  //@ assert \false;
  //@ assert \forall integer x; x > x;
  //@ assert \forall integer x,y,z ; x == y == z == 42;
  return *(int*) 0;
}

Tout est prouvé, y compris que le déréférencement de l’adresse 0 est OK :

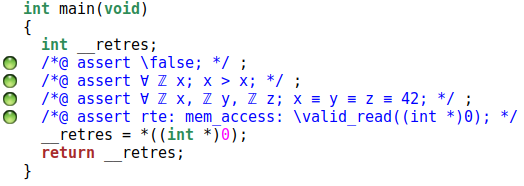
Évidemment cet exemple est extrême, nous n’écririons pas un tel axiome. Le problème est qu’il est très facile d’écrire une axiomatique subtilement fausse lorsque nous exprimons des propriétés plus complexes, ou que nous commençons à poser des suppositions sur l’état global d’un système.

Quand nous commençons à créer de telles définitions, ajouter de temps en temps une preuve ponctuelle de « false » dont nous voulons qu’elle échoue permet de s’assurer que notre définition n’est pas inconsistante. Mais cela ne fait pas tout ! Si la subtilité qui crée le comportement faux est suffisamment cachée, les prouveurs peuvent avoir besoin de beaucoup d’informations autre que l’axiomatique elle-même pour être menés jusqu’à l’inconsistance, donc il faut toujours être vigilant !

Notamment parce que, par exemple, la mention des valeurs lues par une fonction ou un prédicat défini axiomatiquement est également importante pour la consistance de l’axiomatique. En effet, comme mentionné précédemment, si nous n’exprimons pas les valeurs lues dans le cas de l’usage d’un pointeur, la modification d’une valeur du tableau n’invalide pas une propriété que l’on connaîtrait à propos du contenu du tableau par exemple. Dans un tel cas, la preuve passe mais l’axiome n’exprimant pas le contenu, nous ne prouvons rien.

Par exemple, si nous reprenons l’exemple de mise à zéro, nous pouvons modifier la définition de notre axiomatique en retirant la mention des valeurs dont dépendent le prédicat : reads a[b .. e-1]. La preuve passera toujours, mais n’exprimera plus rien à propos du contenu des tableaux considérés. Par exemple, la fonction suivante :

/*@
  requires length > 10 ;
  requires \valid(array + (0 .. length-1));
  requires zeroed(array,0,length);
  assigns  array[0 .. length-1];
  ensures  zeroed(array,0,length);
*/
void bad_function(int* array, size_t length){
  array[5] = 42 ;
}

est prouvée correcte alors qu’une valeur a changé dans le tableau et donc elle n’est plus 0.

Notons qu’à la différence des définitions inductives, où Why3 nous permet de contrôler que ce que nous écrivons est relativement bien défini, nous n’avons pas de mécanisme de ce genre pour les définitions axiomatiques. Ces axiomes sont simplement traduits comme axiomes aussi du côté de Why3 et sont donc supposés vrais.

Exemple : comptage de valeurs

Dans cet exemple, nous cherchons à prouver qu’un algorithme compte bien les occurrences d’une valeur dans un tableau. Nous commençons par définir axiomatiquement la notion de comptage dans un tableau :

/*@
  axiomatic Occurrences_Axiomatic{
    logic integer l_occurrences_of{L}(int value, int* in, integer from, integer to)
      reads in[from .. to-1];

    axiom occurrences_empty_range{L}:
      \forall int v, int* in, integer from, to;
        from >= to ==> l_occurrences_of{L}(v, in, from, to) == 0;

    axiom occurrences_positive_range_with_element{L}:
      \forall int v, int* in, integer from, to;
        (from < to && in[to-1] == v) ==>
      l_occurrences_of(v,in,from,to) == 1+l_occurrences_of(v,in,from,to-1);

    axiom occurrences_positive_range_without_element{L}:
      \forall int v, int* in, integer from, to;
        (from < to && in[to-1] != v) ==>
      l_occurrences_of(v,in,from,to) == l_occurrences_of(v,in,from,to-1);
  }
*/

Nous avons trois cas à gérer :

• la plage de valeur concernée est vide : le nombre d’occurrences est 0 ;
• la plage de valeur n’est pas vide et le dernier élément est celui recherché : le nombre d’occurrences est le nombre d’occurrences dans la plage actuelle que l’on prive du dernier élément, plus 1 ;
• la plage de valeur n’est pas vide et le dernier élément n’est pas celui recherché : le nombre d’occurrences est le nombre d’occurrences dans la plage privée du dernier élément.

Par la suite, nous pouvons écrire la fonction C exprimant ce comportement et la prouver :

/*@
  requires \valid_read(in+(0 .. length));
  assigns  \nothing;
  ensures  \result == l_occurrences_of(value, in, 0, length);
*/
size_t occurrences_of(int value, int* in, size_t length){
  size_t result = 0;
  
  /*@
    loop invariant 0 <= result <= i <= length;
    loop invariant result == l_occurrences_of(value, in, 0, i);
    loop assigns i, result;
    loop variant length-i;
  */
  for(size_t i = 0; i < length; ++i)
    result += (in[i] == value)? 1 : 0;

  return result;
}

Une alternative au fait de spécifier que dans ce code result est au maximum i est d’exprimer un lemme plus général à propos de la valeur du nombre d’occurrences, dont nous savons qu’elle est comprise entre 0 et la taille maximale de la plage de valeurs considérée :

/*@
lemma l_occurrences_of_range{L}:
  \forall int v, int* array, integer from, to:
    from <= to ==> 0 <= l_occurrences_of(v, a, from, to) <= to-from;
*/

La preuve de ce lemme ne pourra pas être déchargée par un solveur automatique. Il faudra faire cette preuve interactivement avec Coq par exemple. Exprimer des lemmes généraux prouvés manuellement est souvent une bonne manière d’ajouter des outils aux prouveurs pour manipuler plus efficacement les axiomatiques, sans ajouter formellement d’axiomes qui augmenteraient nos chances d’introduire des erreurs. Ici, nous devrons quand même réaliser les preuves des propriétés mentionnées.

Exemple: la fonction strlen

Dans cette section, prouvons la fonction C strlen :

#include <stddef.h>

size_t strlen(char const *s){
  size_t i = 0 ;
  while(s[i] != '\0'){
    ++i;
  }
  return i ;
}

Premièrement, nous devons fournir un contrat adapté. Supposons que nous avons une fonction logique strlen qui retourne la longueur d’une chaîne de caractères, à savoir ce que nous attendons de notre fonction C.

/*@
  logic integer strlen(char const* s) = // on verra plus tard
*/

Nous voulons recevoir une chaîne C valide en entrée et nous voulons en calculer la longueur, une valeur qui correspond à celle fournie par la fonction logique strlen appliquée à cette chaîne. Bien sûr, cette fonction n’affecte rien. Définir ce qu’est une chaîne valide n’est pas si simple. En effet, précédemment dans ce tutoriel, nous avons uniquement travaillé avec des tableaux, en recevant en entrée à la fois un pointeur vers le tableau et la taille du dit tableau. Cependant ici, et tel que c’est généralement fait en C, nous supposons que la chaîne termine avec un caractère '\0'. Cela signifie que nous avons en fait besoin de la fonction logique strlen pour définir ce qu’est une chaîne valide. Utilisons d’abord cette définition (notons que nous utilisons \valid_read car nous ne modifions pas la chaîne) pour fournir un contrat pour strlen :

/*@
  predicate valid_read_string(char * s) =
    \valid_read(s + (0 .. strlen(s))) ;
*/

/*@
  requires valid_read_string(s) ; 
  assigns \nothing ;
  ensures \result == strlen(s) ;
*/
size_t strlen(char const *s);

Définir la fonction logique strlen n’est pas si simple. En effet, nous devons calculer la fonction d’une chaîne en trouvant le caractère '\0', et nous espérons le trouver mais en fait, nous pouvons facilement imaginer une chaîne qui n’en contiendrait pas. Dans ce cas, nous voudrions avoir une valeur d’erreur, mais il est impossible de garantir que le calcul termine : une fonction logique ne peut donc pas être utilisée pour exprimer cette propriété.

Définissons donc cette fonction axiomatiquement. D’abord définissons ce qui est lu par la fonction, à savoir : toute position mémoire depuis le pointeur jusqu’à une plage infinie d’adresses. Ensuite, considérons deux cas : la chaîne est finie, ou elle ne l’est pas, ce qui nous amène à deux axiomes : strlen retourne une valeur positive qui correspond à l’indice du premier caractère '\0', et retourne une valeur négative s’il n’y a pas de tel caractère.

/*@
  axiomatic StrLen {
    logic integer strlen(char * s) reads s[0 .. ] ;
    
    axiom pos_or_nul{L}:
      \forall char* s, integer i ;
        (0 <= i && (\forall integer j ; 0 <= j < i ==> s[j] != '\0') && s[i] == '\0') ==>
      strlen(s) == i ;
    axiom no_end{L}:
      \forall char* s ;
        (\forall integer i ; 0 <= i ==> s[i] != '\0') ==> strlen(s) < 0 ;
  }
*/

Maintenant, nous pouvons être plus précis dans notre définition de valid_read_string, une chaîne valide est une chaîne telle qu’est valide depuis le premier indice jusqu’à strlen de la chaîne, et telle que cette valeur est plus grande que 0 (puisqu’une chaîne infinie n’est pas valide) :

/*@
  predicate valid_read_string(char * s) =
    strlen(s) >= 0 && \valid_read(s + (0 .. strlen(s))) ;
*/

Avec cette nouvelle définition, nous pouvons avancer et fournir un invariant utilisable pour la boucle de la fonction strlen. Il est plutôt simple : i est compris entre 0 et strlen(s), pour toute valeur entre 0 et i, elles sont différentes de '\0'. Cette boucle n’affecte que i et le variant correspond à la distance entre i et strlen(s). Cependant, si nous essayons de prouver cette fonction, la preuve échoue. Pour avoir plus d’information, nous pouvons relancer la preuve avec la vérification d’absence de RTE, avec la vérification de non débordement des entiers non signés :

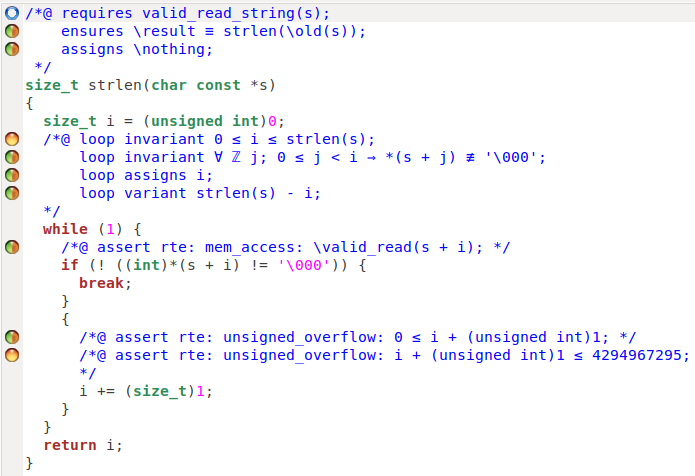
Nous pouvons voir que le prouveur échoue à montrer la propriété liée à la plage de valeur de i, et que i peut excéder la valeur maximale d’un entier non signé. Nous pouvons essayer de fournir une limite à la valeur de strlen(s) en précondition.

  requires valid_read_string(s) && strlen(s) <= UINT_MAX ;

Cependant, c’est insuffisant. La raison et que si nous avons défini la valeur de strlen(s) comme l’index du premier '\0' dans le tableau, l’inverse n’est pas vrai : savoir que la valeur de strlen(s) est positive n’est pas suffisant pour déduire que la valeur à l’indice correspondant est '\0'. Nous étendons donc notre définition axiomatique avec une autre proposition indiquant cette propriété (nous ajoutons également une autre proposition à propos des valeurs qui précèdent cet indice même si ici, ce n’est pas nécessaire) :

/*@
  ...
    axiom index_of_strlen{L}:
      \forall char* s ;
        strlen(s) >= 0 ==> s[strlen(s)] == '\0' ;
    axiom before_strlen{L}:
      \forall char* s ;
        strlen(s) >= 0 ==> (\forall integer i ; 0 <= i < strlen(s) ==> s[i] != '\0') ;
*/

Cette fois la preuve réussit. Frama-C fournit ses propres headers pour la bibliothèque standard, et cela inclut une définition axiomatique pour la fonction logique strlen. Elle peut être trouvée dans le dossier de Frama-C, sous le dossier libc, le fichier est nommé __fc_string_axiomatic.h. Notons que cette définition a beaucoup plus d’axiomes pour déduire plus de propriétés à propos de strlen.

Exercices

Comptage d’occurrences

Le programme suivant ne peut pas être prouvé avec la définition axiomatique que nous avons défini précédemment à propos du comptage d’occurrences :

/*@
  requires \valid_read(in+(0 .. length));
  assigns  \nothing;
  ensures  \result == l_occurrences_of(value, in, 0, length);
*/
size_t occurrences_of(int value, int* in, size_t length){
  size_t result = 0;
  
  for(size_t i = length; i > 0 ; --i)
    result += (in[i-1] == value) ? 1 : 0;

  return result;
}

Ré-exprimer la définition axiomatique dans une forme qui permet de prouver le programme.

Plus grand diviseur commun

Exprimer la fonction logique qui calcule le plus grand diviseur commun à l’aide d’une définition axiomatique et écrire le contrat de la fonction gcd puis la prouver.

#include <limits.h>

/*@ 
  axiomatic GCD {
    // ...
  }
*/

/*@
  requires a >= 0 && b >= 0 ;
  // assigns ...
  // ensures ...
*/
int gcd(int a, int b){
  while (b != 0){
    int t = b;
    b = a % b;
    a = t;
  }
  return a;
}

Somme des N premiers entiers

Exprimer la fonction logique qui calcule la somme des N premiers entiers à l’aide d’une définition axiomatique. Écrire le contrat de la fonction sum_n et la prouver :

#include <limits.h>

/*@ axiomatic Sum_n {
      // ...
    }
*/

/*@ lemma sum_n_value: // ... */

/*@ 
  requires n >= 0 ;
  // requires ...
  // assigns ...
  // ensures ...
*/
int sum_n(int n){
  if(n < 1) return 0 ;

  int res = 0 ;
  /*@ loop invariant 1 <= i <= n+1 ;
      // ...
  */
  for(int i = 1 ; i <= n ; i++){
    res += i ;
  }
  return res ;
}

Permutation

Reprendre l’exemple à propos du tri par sélection produit dans la section sur les définitions inductives. Ré-exprimer le prédicat de permutation comme une définition axiomatique. Prendre garde à la clause reads (en particulier, noter que le prédicat relie deux labels mémoire).

/*@
  axiomatic Permutation {
    // ...
  }
*/

/*@
  predicate sorted(int* a, integer b, integer e) =
    \forall integer i, j; b <= i <= j < e ==> a[i] <= a[j];
*/

/*@
  requires beg < end && \valid(a + (beg .. end-1));
  assigns  a[beg .. end-1];  
  ensures sorted(a, beg, end);
  ensures permutation{Pre, Post}(a,beg,end);
*/
void sort(int* a, size_t beg, size_t end){
  /*@
    loop invariant beg <= i <= end;
    loop invariant sorted(a, beg, i) && permutation{Pre, Here}(a, beg, end);
    loop invariant \forall integer j,k; beg <= j < i ==> i <= k < end ==> a[j] <= a[k];
    loop assigns i, a[beg .. end-1];
    loop variant end-i;
  */
  for(size_t i = beg ; i < end ; ++i){
    //@ ghost begin: ;
    size_t imin = min_idx_in(a, i, end);
    swap(&a[i], &a[imin]);
    //@ assert swap_in_array{begin,Here}(a,beg,end,i,imin);
  }
}

Les techniques que nous avons vu précédemment dans ce chapitre ont pour but de rendre la spécification plus abstraite. Le rôle du code fantôme est inverse. Ici, nous enrichirons nos spécifications à l’aide d’information exprimées en langage C. L’idée est d’ajouter des variables et du code source qui n’intervient pas dans le programme réel mais permettant de créer des états logiques qui ne seront visibles que depuis la preuve. Par cet intermédiaire, nous pouvons rendre explicites des propriétés logiques qui étaient auparavant implicites.

Syntaxe

Le code fantôme est ajouté par l’intermédiaire d’annotations qui contiennent du code C ainsi que la mention ghost.

/*@
  ghost
  // code en langage C
*/

Dans un code fantôme, nous écrivons du C normal. Nous expliquerons certaines petites subtilités plus tard. Pour l’instant, intéressons nous aux éléments basiques que nous pouvons écrire avec du code fantôme.

Nous pouvons déclarer des variables :

//@ ghost int ghost_glob_var = 0;

void foo(int a){
  //@ ghost int ghost_loc_var = a;
}

Ces variables peuvent être modifiées via des opérations et structures conditionnelles :

//@ ghost int ghost_glob_var = 0;

void foo(int a){
  //@ ghost int ghost_loc_var = a;
  /*@ ghost
    for(int i = 0 ; i < 10 ; i++){
      ghost_glob_var += i ;
      if(i < 5) ghost_local_var += 2 ;
    }
  */
}

Nous pouvons déclarer des labels fantômes, que l’on peut utiliser dans nos annotations (ou même pour effectuer un goto depuis le code fantôme lui-même, sous certaines conditions que nous expliquerons plus tard) :

void foo(int a){
  //@ ghost Ghost_label: ;
  a = 28 ;
  //@ assert ghost_loc_var == \at(a, Ghost_label) == \at(a, Pre);
}

Une construction conditionnelle if peut être étendue avec un else fantôme s’il n’a pas de else à la base. Par exemple :

void foo(int a){
  //@ ghost int a_was_ok = 0 ;
  if(a < 5){
    a = 5 ;
  } /*@ ghost else {
    a_was_ok = 1 ;
  } */
}

Une fonction peut avoir des paramètres fantômes, cela permet de transmettre des informations supplémentaires pour la vérification de la fonction. Par exemple, si l’on imagine la vérification d’une fonction qui reçoit une liste chaînée, nous pourrions transmettre un paramètre fantôme qui représenterait la longueur de la liste :

void function(struct list* l) /*@ ghost (int length) */ {
  // visit the list
  /*@ variant length ; */
  while(l){
    l = l->next ;
    //@ ghost length--;
  }
}
void another_function(struct list* l){
  //@ ghost int length ;

  // ... do something to compute the length

  function(l) /*@ ghost(n) */ ; // we call 'function' with the ghost argument
}

Notons que si une fonction prend des paramètres fantômes, tous les appels doivent fournir les arguments fantômes correspondant.

Une fonction toute entière peut être fantôme. Par exemple, nous pourrions avoir une fonction fantôme qui calcule la longueur d’une liste que nous aurions utilisée au sein du code précédent :

/*@ ghost
  /@ ensures \result == logic_length_of_list(l) ; @/
  int compute_length(struct list* l){
    // does the right computation
  }
*/

void another_function(struct list* l){
  //@ ghost int length ;

  //@ ghost length = compute_length(l) ;
  function(l) /*@ ghost(n) */ ; // we call 'function' with the ghost argument
}

Ici, nous pouvons voir une syntaxe spécifique pour le contrat de la fonction fantôme. En effet, il est souvent utile d’écrire des contrats ou des assertions dans du code fantôme. Comme nous devons écrire ces spécifications dans du code qui est déjà englobé dans des commentaires C, nous avons accès à une syntaxe spécifique pour fournir des contrats ou des assertions fantômes. Nous ouvrons une annotation fantôme avec la syntaxe /@ et nous la fermons avec @/. Cela s’applique aussi aux boucles dans le code fantôme par exemple :

void foo(unsigned n){
 /*@ ghost
   unsigned i ;

   /@
     loop invariant 0 <= i <= n ;
     loop assigns i ;
     loop variant n - i ;
   @/
   for(i = 0 ; i < n ; ++i){

   }
   /@ assert i == n ; @/
 */
}

Validité du code fantôme, ce que Frama-C vérifie

Frama-C vérifie plusieurs propriétés à propos du code fantôme que nous écrivons :

• le code fantôme ne peut pas modifier le graphe de flot de contrôle du programme ;
• le code normal ne peut pas accéder à la mémoire fantôme ;
• le code fantôme ne peut modifier qu’une zone de mémoire fantôme.

Très simplement, ces propriétés cherchent à garantir que pour n’importe quel programme, son comportement observable pour toute entrée est le même avec ou sans le code fantôme.

Si certaines de ces propriétés ne sont pas vérifiées, cela voudrait dire que le code fantôme peut changer le comportement du programme vérifié. Analysons de plus prêt chacune de ces contraintes.

Maintien du flot de contrôle

Le flot de contrôle d’un programme est l’ordre dans lequel les instructions sont exécutées par le programme. Si le code fantôme change cet ordre, ou permet de ne plus exécuter certaines instructions du programme d’origine, alors le comportement du programme n’est plus le même, et nous ne vérifions donc plus le même programme.

Par exemple, la fonction suivante calcule la somme des $n$ premiers entiers :

int sum(int n){
  int x = 0 ;
  for(int i = 0; i <= n; ++i){
    //@ ghost break;
    x += i ;
  }
  return x;
}

Par l’introduction, dans du code fantôme, de l’instruction break dans le corps de la boucle, le programme n’a plus le même comportement : au lieu de parcourir l’ensemble des $i$ de $0$ à $n+1$, la boucle s’arrête dès la première itération. En conséquence, ce programme sera rejeté par Frama-C :

[kernel:ghost:bad-use] file.c:4: Warning:
  Ghost code breaks CFG starting at:
  /*@ ghost break; */
  x += i;

Il est important de noter que lorsqu’un code fantôme altère le flot de contrôle c’est le point de départ du code fantôme qui est pointé par l’erreur, par exemple si nous introduisons une conditionnelle autour de notre break :

int sum(int n){
  int x = 0 ;
  for(int i = 0; i <= n; ++i){
    //@ ghost if(i < 3) break;
    x += i ;
  }
  return x;
}

Le problème est indiqué pour le if englobant :

[kernel:ghost:bad-use] file.c:4: Warning:
  Ghost code breaks CFG starting at:
  /*@ ghost if (i < 3) break; */
  x += i;

Notons que la vérification que le flot de contrôle n’est pas altéré est purement syntaxique. Par exemple, si le break est inatteignable parce que la condition est toujours fausse, une erreur sera quand même levée :

int sum(int n){
  int x = 0 ;
  for(int i = 0; i <= n; ++i){
    //@ ghost if(i > n) break;
    x += i ;
  }
  return x;
}

nous donne :

[kernel:ghost:bad-use] file.c:4: Warning:
  Ghost code breaks CFG starting at:
  /*@ ghost if (i > n) break; */
  x += i;

Finalement, remarquons qu’il existe deux manières générales d’altérer le flot de contrôle. La première est d’utiliser un saut (donc break, continue, ou goto), la seconde est d’introduire un code non terminant. Pour ce dernier, à moins que le code soit trivialement non terminant, le noyau ne peut pas vérifier la non-altération du flot de contrôle, et ne le fait donc jamais. Nous traiterons cette question dans une section à venir.

Accès à la mémoire

Le code fantôme est un observateur du code normal. En conséquence, le code normal n’est pas autorisé à accéder au code fantôme, que ce soit sa mémoire ou ses fonctions. Le code fantôme lui, peut lire la mémoire du code normal, mais ne peut pas la modifier. Actuellement, le code fantôme ne peut pas non plus appeler de fonctions du code normal, nous parlerons de cette restriction à la fin de cette section.

Refuser que le code normal voie le code fantôme a une raison toute simple, si le code normal tentait d’accéder à des variables fantômes, il ne pourrait même pas être compilé : le compilateur ne voit pas les variables déclarées dans les annotations. Par exemple :

int sum_42(int n){
  int x = 0 ;
  //@ ghost int r = 42 ;
  for(int i = 0; i < n; ++i){
    x += r;
  }
  return x;
}

ne peut pas être compilé :

# gcc -c file.c
file.c: In function ‘sum_42’:
file.c:5:10: error: ‘r’ undeclared (first use in this function)
    5 |     x += r;
      |          ^

et n’est donc pas accepté par Frama-C non plus :

[kernel] file.c:5: User Error:
  Variable r is a ghost symbol. It cannot be used in non-ghost context. Did you forget a /*@ ghost ... /?

Dans le code fantôme, les variables normales ne doivent pas être modifiées. En effet, cela impliquerait de pouvoir par exemple modifier le résultat d’un programme en ajoutant du code fantôme. Par exemple dans le code suivant :

int sum(int n){
  int x = 0 ;
  for(int i = 0; i <= n; ++i){
    x += i ;
    //@ ghost x++;
  }
  return x;
}

Le résultat du programme ne serait pas le même avec ou sans le code fantôme. Frama-C interdit donc un tel code :

[kernel:ghost:bad-use] file.c:5: Warning:
  'x' is a non-ghost lvalue, it cannot be assigned in ghost code

Notons que cette vérification est faite grâce au type des différentes variables. Une variable déclarée dans du code normal a un statut de variable normale, tandis qu’une variable déclarée dans du code fantôme a un statut de variable fantôme. Par conséquent, une nouvelle fois, même si le code fantôme, dans les faits, n’altère pas le comportement du programme, toute écriture d’une variable normale dans le code fantôme est interdite :

int sum(int n){
  int x = 0 ;
  for(int i = 0; i <= n; ++i){
    x += i ;
    /*@ ghost
      if (x < INT_MAX){
        x++;
    x--; // assure that x remains coherent
      }
    */
  }
  return x;
}

nous donne :

[kernel:ghost:bad-use] file.c:9: Warning:
  'x' is a non-ghost lvalue, it cannot be assigned in ghost code
[kernel:ghost:bad-use] file.c:10: Warning:
  'x' is a non-ghost lvalue, it cannot be assigned in ghost code

Cela s’applique également à la clause assigns lorsqu’elle est dans du code fantôme :

int x ;

/*@ ghost
  /@ assigns x ; @/
  void ghost_foo(void);
*/

void foo(void){
  /*@ ghost
    /@ assigns x ; @/
    for(int i = 0; i < 10; ++i);
  */
}

qui donne :

[kernel:ghost:bad-use] file.c:4: Warning:
  'x' is a non-ghost lvalue, it cannot be assigned in ghost code
[kernel:ghost:bad-use] file.c:11: Warning:
  'x' is a non-ghost lvalue, it cannot be assigned in ghost code

En revanche, les contrats des fonctions et boucles normales peuvent (et doivent) permettre de spécifier les zones de mémoire fantôme modifiées. Par exemple, si nous corrigeons le petit programme précédent en rendant x fantôme, d’une part nos clauses assigns précédentes sont bien acceptées, mais en plus, nous pouvons spécifier que la fonction foo modifie la variable globale fantôme x :

//@ ghost int x ;

/*@ ghost
  /@ assigns x ; @/
  void ghost_foo(void);
*/

/*@ assigns x ; */
void foo(void){
  /*@ ghost
    /@ assigns x ; @/
    for(int i = 0; i < 10; ++i);
  */
}

Typage des éléments fantômes

Il convient de donner quelques précisions au sujet des types des variables créées dans du code fantôme. Par exemple, parfois il est intéressant de pouvoir créer un tableau fantôme pour stocker des informations :

void function(int a[5]){
  //@ ghost int even[5] = { 0 };

  for(int i = 0; i < 5; ++i){
    //@ ghost if(a[i] % 2) even[i] = 1;
  }
}

Ici, nous utilisons des indices pour accéder à nos tableaux, mais nous pourrions par exemple vouloir y accéder en utilisant un pointeur :

void function(int a[5]){
  //@ ghost int even[5] = { 0 };
  //@ ghost int *pe = even ;

  for(int *p = a; p < a+5; ++p){
    //@ ghost if(*p % 2) *pe = 1;
    //@ ghost pe++;
  }
}

Mais nous voyons immédiatement que Frama-C n’est pas d’accord avec notre manière de faire :

[kernel:ghost:bad-use] file.c:3: Warning:
  Invalid cast of 'even' from 'int \ghost *' to 'int *'
[kernel:ghost:bad-use] file.c:6: Warning:
  '*pe' is a non-ghost lvalue, it cannot be assigned in ghost code

En particulier, le premier message nous indique que nous essayons de transformer un pointeur sur int \ghost en pointeur sur int. En effet, lorsqu’une variable est déclarée dans du code fantôme, seule la variable est considérée fantôme. Donc dans le cas d’un pointeur, la mémoire pointée par ce pointeur, elle, n’est pas considérée comme fantôme (et donc ici, bien que pe soit fantôme, la mémoire pointée par pe ne l’est pas). Pour résoudre ce problème, Frama-C nous offre le qualificateur \ghost, qui nous permet d’ajouter un caractère fantôme à un type :

void function(int a[5]){
  //@ ghost int even[5] = { 0 };
  //@ ghost int \ghost * pe = even ;

  for(int *p = a; p < a+5; ++p){
    //@ ghost if(*p % 2) *pe = 1;
    //@ ghost pe++;
  }
}

Sur certains aspects, le qualificateur \ghost ressemble au mot-clé const du C. Cependant, son comportement n’est pas exactement le même pour deux raisons.

Tout d’abord, alors que la définition const suivante est autorisée, il n’est pas possible d’avoir une déclaration de forme similaire avec le qualificateur \ghost :

int const * * const p ;
//@ ghost int \ghost * * p ;

produit l’erreur :

[kernel:ghost:bad-use] file.c:2: Warning:
  Invalid type for 'p': indirection from non-ghost to ghost

Déclarer un pointeur constant sur une zone que l’on peut modifier et qui contient des pointeurs vers de la mémoire constante ne pose pas de problème. En revanche, il est impossible de faire de même avec le qualificateur \ghost, cela signifierait que la mémoire normale contient des pointeurs vers la mémoire fantôme, ce qui n’est pas possible.

D’autre part, il est possible d’assigner un pointeur vers des données non-constantes à un pointeur vers des données constantes :

int a[10] ;
int const * p = a ;

Ce code ne pose pas de problème, car l’on ne fait que restreindre notre capacité à modifier les données lorsque l’on initialise (ou affecte) p à &a[0]. En revanche, les deux initialisations (ou affectations équivalentes) des pointeurs suivants sont refusées avec le qualificateur \ghost :

int non_ghost_int ;
//@ ghost int ghost_int ;

//@ ghost int \ghost * p = & non_ghost_int ;
//@ ghost int * q = & ghost_int ;

Si la raison du refus de la première initialisation est tout à fait directe : elle permettrait de modifier le contenu de la mémoire normale depuis du code fantôme, refuser la seconde peut être un peu moins intuitif. Et en effet, nous devons passer par des moyens détournés pour provoquer un problème avec cette conversion :

/*@ ghost
  /@ assigns *p ; 
     ensures *p == \old(*q); @/
  void assign(int * \ghost * p, int * \ghost * q){
    *p = *q ;
  }
*/
void caller(void){
  int x ;
  
  //@ ghost int \ghost * p ;
  //@ ghost int * q = &x ;
  //@ ghost assign(&p, &q) ;
  //@ ghost *p = 42 ; 
}

Ici, nous faisons une conversion qui pourrait sembler autorisée. En effet, nous passons l’adresse d’un pointeur sur une zone de mémoire fantôme à une fonction qui attend un pointeur sur une zone de mémoire normale, cela ne fait que restreindre l’accès à la mémoire pointée. Cependant, par cet appel de fonction, la fonction assign assigne la valeur actuelle de q (qui est \CodeInline&x) à p et nous permet donc, par la dernière opération de modifier x dans du code fantôme. En conséquence, une telle conversion n’est jamais autorisée.

Finalement, le code fantôme ne peut actuellement pas appeler de fonction non fantôme, pour des raisons semblables à celle évoquée pour l’interdiction de toutes les conversions. Certains cas particuliers pourraient être traités de manière à accepter plus de code, mais ce n’est actuellement pas supporté par Frama-C.

Validité du code fantôme, ce qu’il reste à vérifier

Mis à part les restrictions que nous avons mentionnées dans la section précédente, le code fantôme est juste du code C normal. Cela veut dire que si nous voulons faire la vérification de notre programme d’origine, nous devons faire attention, nous-mêmes, à au moins deux aspects supplémentaires :

• l’absence d’erreurs à l’exécution,
• la terminaison du code fantôme.

Le premier cas ne nécessite pas plus d’attention que le reste de notre code. En effet, la vérification d’absence d’erreurs à l’exécution sera traitée par le plugin RTE comme pour le reste de notre programme.

Comme nous l’avons dit dans la section sur les variants de boucle, il y a deux sortes de correction : la correction partielle et la correction totale, la seconde permettant de prouver qu’un programme termine. Dans le cas du code normal, montrer la terminaison n’est pas toujours souhaitable pour l’ensemble du programme. En revanche, si nous utilisons du code fantôme pour aider la vérification, montrer que la correction est totale est absolument nécessaire car une boucle infinie dans le code fantôme peut nous permettre de prouver n’importe quoi à propos du programme.

/*@ ensures \false ; */
void foo(void){
  /*@ ghost
    while(1){}
  */
}

Expliciter un état logique

Le but du code fantôme est de rendre explicite des informations généralement implicites. Par exemple, dans la vérification de l’algorithme de tri, nous nous en sommes servi pour ajouter un label dans le programme qui n’est pas visible par le compilateur, mais que nous avons pu utiliser pour la vérification. Le fait que les valeurs ont été échangées entre les deux points de programme était implicitement garanti par le contrat de la fonction d’échange, ajouter ce label fantôme nous a donné la possibilité de rendre cette propriété explicite par une assertion.

Prenons maintenant un exemple plus poussé. Nous voulons par exemple prouver que la fonction suivante nous retourne la valeur maximale des sommes de sous-tableaux possibles d’un tableau donné. Un sous-tableau d’un tableau a est un sous-ensemble contigu de valeur de a. Par exemple, pour un tableau { 0 , 3 , -1 , 4 }, des exemples de sous tableaux peuvent être {}, { 0 }, { 3 , -1 } , { 0 , 3 , -1 , 4 }, … Notons que comme nous autorisons le tableau vide, la somme est toujours au moins égale à 0. Dans le tableau précédent, le sous-tableau de valeur maximale est { 3 , -1 , 4 }, la fonction renverra donc 6.

int max_subarray(int *a, size_t len) {
  int max = 0;
  int cur = 0;
  for(size_t i = 0; i < len; i++) {
    cur += a[i];
    if (cur < 0)   cur = 0;
    if (cur > max) max = cur;
  }
  return max;
}

Pour spécifier la fonction précédente, nous aurons besoin d’exprimer axiomatiquement la somme. Ce n’est pas très complexe, et le lecteur pourra s’exercer en exprimant les axiomes nécessaires au bon fonctionnement de cette axiomatique :

/*@ axiomatic Sum {
  logic integer sum(int *array, integer begin, integer end) reads a[begin..(end-1)];
}*/

La correction est cachée ici :

/*@
  axiomatic Sum_array{
    logic integer sum(int* array, integer begin, integer end) reads array[begin .. (end-1)];
   
    axiom empty: 
      \forall int* a, integer b, e; b >= e ==> sum(a,b,e) == 0;
    axiom range:
      \forall int* a, integer b, e; b < e ==> sum(a,b,e) == sum(a,b,e-1)+a[e-1];
  }
*/

La spécification de notre fonction est la suivante :

/*@ 
  requires \valid(a+(0..len-1));
  assigns \nothing;
  ensures \forall integer l, h;  0 <= l <= h <= len ==> sum(a,l,h) <= \result;
  ensures \exists integer l, h;  0 <= l <= h <= len &&  sum(a,l,h) == \result;
*/

Pour toute paire de bornes, la valeur retournée par la fonction doit être supérieure ou égale à la somme des éléments entre les bornes, et il doit exister une paire de bornes telle que la somme des éléments entre ces bornes est exactement la valeur retournée par la fonction. Par rapport à cette spécification, si nous devons ajouter les invariants de boucles, nous nous apercevons rapidement qu’il nous manquera des informations. Nous avons besoin d’exprimer ce que sont les valeurs max et cur et quelles relations existent entre elles, mais rien ne nous le permet !

En substance, notre postcondition a besoin de savoir qu’il existe des bornes low et high telles que la somme calculée correspond à ces bornes. Or, notre code n’exprime rien de tel d’un point de vue logique et rien ne nous permet a priori de faire cette liaison en utilisant des formulations logiques. Nous utiliserons donc du code ghost pour conserver ces bornes et exprimer l’invariant de notre boucle.

Nous aurons d’abord besoin de deux variables qui nous permettront de stocker les valeurs des bornes de la plage maximum, nous les appellerons low et high. Chaque fois que nous trouverons une plage où la somme est plus élevée nous les mettrons à jour. Ces bornes correspondront donc à la somme indiquée par max. Cela induit que nous avons encore besoin d’une autre paire de bornes : celle correspondant à la variable de somme cur à partir de laquelle nous pourrons construire les bornes de max. Pour celle-ci, nous n’avons besoin que d’ajouter une variable ghost : le minimum actuel cur_low, la borne supérieure de la somme actuelle étant indiquée par la variable i de la boucle.

/*@ 
  requires \valid(a+(0..len-1));
  assigns \nothing;
  ensures \forall integer l, h;  0 <= l <= h <= len ==> sum(a,l,h) <= \result;
  ensures \exists integer l, h;  0 <= l <= h <= len &&  sum(a,l,h) == \result;
*/
int max_subarray(int *a, size_t len) {
  int max = 0;
  int cur = 0;
  //@ ghost size_t cur_low = 0; 
  //@ ghost size_t low = 0;
  //@ ghost size_t high = 0; 

  /*@ 
    loop invariant BOUNDS: low <= high <= i <= len && cur_low <= i;
    
    loop invariant REL :   cur == sum(a,cur_low,i) <= max == sum(a,low,high);
    loop invariant POST:   \forall integer l;    0 <= l <= i      ==> sum(a,l,i) <= cur;
    loop invariant POST:   \forall integer l, h; 0 <= l <= h <= i ==> sum(a,l,h) <= max;
   
    loop assigns i, cur, max, cur_low, low, high;
    loop variant len - i; 
  */
  for(size_t i = 0; i < len; i++) {
    cur += a[i];
    if (cur < 0) {
      cur = 0;
      /*@ ghost cur_low = i+1; */
    }
    if (cur > max) {
      max = cur;
      /*@ ghost low = cur_low; */
      /*@ ghost high = i+1; */
    }
  }
  return max;
}

L’invariant BOUNDS exprime comment sont ordonnées les différentes bornes pendant le calcul. L’invariant REL exprime ce que signifient les valeurs cur et max par rapport à ces bornes. Finalement, l’invariant POST permet de faire le lien entre les invariants précédents et la postcondition de la fonction.

Le lecteur pourra vérifier que cette fonction est effectivement prouvée sans la vérification des RTE. Si nous ajoutons également le contrôle des RTE, nous pouvons voir que le calcul de la somme indique un dépassement possible sur les entiers.

Ici, nous ne chercherons pas à le corriger, car ce n’est pas l’objet de l’exemple. Le moyen de prouver cela dépend en fait fortement du contexte dans lequel on utilise la fonction. Une possibilité est de restreindre fortement le contrat en imposant des propriétés à propos des valeurs et de la taille du tableau. Par exemple, nous pourrions imposer une taille maximale et des bornes fortes pour chacune des cellules. Une autre possibilité est d’ajouter une valeur d’erreur en cas de dépassement (par exemple $-1$), et de spécifier qu’en cas de dépassement, c’est cette valeur qui est renvoyée.

Exercices

Validité du code ghost

Dans ces fonctions, sans exécuter Frama-C, expliquer en quoi le code fantôme pose problème. Lorsque Frama-C devrait rejeter le code, expliquer pourquoi. Notons qu’il est possible d’exécuter Frama-C sans contrôle du code fantôme en utilisant l’option -kernel-warn-key ghost=inactive.

#include <stddef.h>
#include <limits.h>

/*@
  assigns \nothing;
  ensures \result == a || \result == b ;
  ensures \result >= a && \result >= b ;
*/
int max(int a, int b){
  int r = INT_MAX;
  //@ ghost r = (a > b) ? a : b ;
  return r ;
}

/*@
  requires \valid(a) && \valid(b);
  assigns *a, *b;
  ensures *a == \old(*b) && *b == \old(*a);
*/
void swap(int* a, int* b){
  int tmp = *a ;
  *a = *b ;
  //@ ghost int \ghost* ptr = b ;
  //@ ghost *ptr = tmp ;
}

/*@
  requires \valid(a+(0 .. len-1));
  assigns  \nothing ;
  ensures \result <==> (\forall integer i ; 0 <= i < len ==> a[i] == 0);
*/
int null_vector(int* a, size_t len){
  //@ ghost int value = len ;
  /*@ loop invariant 0 <= i <= len ;
    loop invariant \forall integer j ; 0 <= j < i ==> a[j] == 0 ;
    loop assigns i ;
    loop variant len-i ;
  */
  for(size_t i = 0 ; i < len ; ++i)
    if(a[i] != 0) return 0;
  /*@ ghost 
    /@ loop assigns \nothing ; @/
    while(value >= len);
  */
  return 0;
}

Multiplication par 2

Le programme suivant calcule 2 * x en utilisant une boucle. Utiliser une variable fantôme i pour exprimer comme invariant que la valeur de r est i * 2 et compléter la preuve.

/*@ 
  requires x >= 0 ;
  assigns  \nothing ;
  ensures  \result == 2 * x ;
*/
int times_2(int x){
  int r = 0 ;
  /*@
    loop invariant 0 <= x ;
    loop invariant r == // ...
    loop invariant // ...
  */
  while(x > 0){
    r += 2 ;
    x -- ;
  }
  return r;
}

Tableaux

Cette fonction reçoit un tableau et effectue une boucle dans laquelle nous ne faisons rien, sauf que nous avons indiqué que le contenu du tableau est modifié. Cependant, nous voudrions pouvoir prouver qu’en postcondition, le tableau n’a pas été modifié.

/*@
  requires \valid(a + (0 .. 9)) ;
  assigns  a[0 .. 9] ;
  ensures  \forall integer j ; 0 <= j < 10 ==> a[j] == \old(a[j]) ;
*/
void foo(int a[10]){
  //@ ghost int g[10] ;
  /*@ ghost
    ...
  */
  
  /*@
    loop invariant 0 <= i <= 10 ;
    loop invariant // ...
    loop assigns i, a[0 .. 9] ;
    loop variant 10 - i ;
  */
  for(int i = 0; i < 10; i++);
}

Sans modifier la clause assigns de la boucle et sans utiliser le mot clé \at, prouver que la fonction ne modifie pas le contenu du tableau. Pour cela, compléter le code fantôme et l’invariant de boucle en assurant que le contenu du tableau g représente l’ancien contenu de a.

Lorsque c’est fait, créer une fonction fantôme qui effectue cette même copie, et l’utiliser dans la fonction foo pour effectuer la même preuve.

Chercher et remplacer

Le programme suivant effectue une opération de recherche et remplacement :

#include <stddef.h>

void replace(int *a, size_t length, int old, int new) {
  for (size_t i = 0; i < length; ++i) {
    if (a[i] == old)
      a[i] = new;
  }
}

/*@
  requires \valid(a + (0 .. length-1));
  assigns a[0 .. length-1];
  ensures \forall integer i ; 0 <= i < length ==> -100 <= a[i] <= 100 ;
*/
void initialize(int *a, size_t length);

void caller(void) {
  int a[40];

  initialize(a, 40);

  //@ ghost L: ;

  replace(a, 40, 0, 42);

  // here we want to obtain the updated locations via a ghost array
}

En supposant que la fonction replace demande à ce que old et new soient différents, écrire un contrat pour replace et prouver que la fonction le satisfait.

Maintenant, nous voudrions savoir quelles cellules du tableau ont été mises à jour par la fonction. Ajouter un paramètre fantôme à la fonction replace de manière à pouvoir recevoir un second tableau qui servira à enregistrer les cellules mises à jour (ou non) par la fonction. En ajoutant également le code suivant après l’appel à replace :

/*@ ghost
  /@ loop invariant 0 <= i <= 40 ;
     loop assigns i;
     loop variant 40 - i ;
  @/
  for(size_t i = 0 ; i < 40 ; ++i){
    if(updated[i]){
      /@ assert a[i] != \at(a[\at(i, Here)], L); @/
    } else {
      /@ assert a[i] == \at(a[\at(i, Here)], L); @/
    }
  }
*/

Tout devrait être prouvé.