ACSL - Propriétés

ACSL fournit différents types logiques qui permettent d’écrire des propriétés dans un monde plus abstrait, plus mathématique. Parmi les types qui peuvent être utiles, certains sont dédiés aux nombres et permettent d’exprimer des propriétés ou des fonctions sans avoir à nous soucier des contraintes dues à la taille en mémoire des types primitifs du C. Ces types sont integer et real, qui représentent respectivement les entiers mathématiques et les réels mathématiques (pour ces derniers, la modélisation est aussi proche que possible de la réalité, mais la notion de réel ne peut pas être parfaitement représentée).

Par la suite, nous utiliserons souvent des entiers à la place des classiques ìnt du C. La raison est simplement que beaucoup de propriétés sont vraies quelle que soit la taille de l’entier (au sens C, cette fois) en entrée.

En revanche, nous ne parlerons pas de real VS float/double, parce que cela induirait que nous parlions de preuve de programmes avec du calcul en virgule flottante et que nous n’en parlerons pas ici. Par contre, ce tutoriel en parle : Introduction à l’arithmétique flottante.

Un prédicat est une propriété portant sur des objets et pouvant être vraie ou fausse. En résumé, des prédicats, c’est ce que nous écrivons depuis le début de ce tutoriel dans les clauses de nos contrats et de nos invariants de boucle. ACSL permet de créer des versions nommées de ces prédicats, à la manière d’une fonction booléenne en C par exemple, à la différence près que les prédicats (ainsi que les fonctions logiques que nous verrons par la suite) doivent être pures, c’est-à-dire qu’elles ne peuvent pas produire d’effets de bords en modifiant des valeurs pointées par exemple.

Ces prédicats peuvent prendre un certain nombre de paramètres. En plus de cela, ils peuvent également recevoir un certain nombre de labels (au sens C du terme) qui permettront d’établir des relations entre divers points du code.

Syntaxe

Les prédicats sont, comme les spécifications, introduits via des annotations. La syntaxe est la suivante :

/*@
  predicate nom_du_predicat { Lbl0, Lbl1, ..., LblN }(type0 arg0, type1 arg1, ..., typeN argN) =
    //une relation logique entre toutes ces choses.
*/

Nous pouvons par exemple définir le prédicat nous disant qu’un entier en mémoire n’a pas changé entre deux points particuliers du programme :

/*@
  predicate unchanged{L0, L1}(int* i) =
    \at(*i, L0) == \at(*i, L1);
*/

/*@
  predicate unchanged{L0, L1}(int i) =
    \at(i, L0) == \at(i, L1);
 */

Nous pouvons par exemple vérifier ce petit code :

int main(){
  int i = 13;
  int j = 37;

 Begin:
  i = 23;
 
  //@assert ! unchanged{Begin, Here}(&i);
  //@assert   unchanged{Begin, Here}(&j);
}

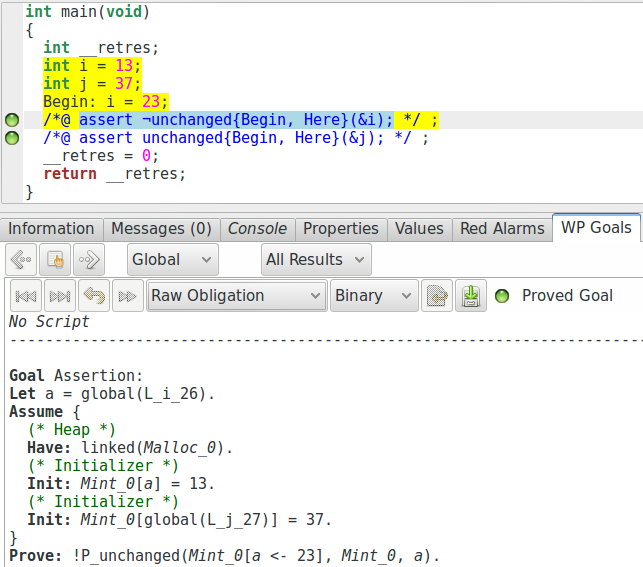
Nous pouvons également regarder les buts générés par WP et constater que, même s’il subit une petite transformation syntaxique, le prédicat n’est pas déroulé par WP. Ce sera au prouveur de déterminer s’il veut raisonner avec.

Comme nous l’avons dit plus tôt, une des utilités des prédicats et fonctions (que nous verrons un peu plus tard) est de rendre plus lisible nos spécifications et de les factoriser. Un exemple est l’écriture d’un prédicat pour la validité en lecture/écriture d’un tableau sur une plage particulière. Cela nous évite d’avoir à réécrire l’expression en question qui est moins compréhensible au premier coup d’œil.

/*@
  predicate valid_range_rw(int* t, integer n) =
    n >= 0 && \valid(t + (0 .. n-1));

  predicate valid_range_ro(int* t, integer n) =
    n >= 0 && \valid_read(t + (0 .. n-1));
*/

/*@
  requires 0 < length;
  requires valid_range_ro(array, length);
  //...
*/
int* search(int* array, size_t length, int element)

Dans cette portion de spécification, le label pour les prédicats n’est pas précisé, ni pour leur création, ni pour leur utilisation. Pour la création, Frama-C en ajoutera automatiquement un dans la définition du prédicat. Pour l’appel, le label passé sera implicitement Here. La non-déclaration du label dans la définition n’interdit pour autant pas de passer explicitement un label lors de l’appel.

Bien entendu, les prédicats peuvent être déclarés dans des fichiers headers afin de produire une bibliothèque d’utilitaires de spécifications par exemple.

Surcharger des prédicats

Il est possible de surcharger les prédicats tant que les types des paramètres sont différents ou que le nombre de paramètres change. Par exemple, nous pouvons redéfinir valid_range_r comme un prédicat qui prend en paramètre à la fois le début et la fin de la plage considérée. Ensuite, nous pouvons écrire une surcharge qui utilise le prédicat précédent pour le cas particulier des plages qui commencent à 0 :

/*@
  predicate valid_range_r(int* t, integer beg, integer end) =
    end >= beg && \valid_read(t + (beg .. end-1)) ;
  predicate valid_range_r(int* t, integer n) =
    valid_range_r(t, 0, n) ;
*/

/*@
  requires 0 < length;
  requires valid_range_r(array, length);
  //...
*/
int* search(int* array, size_t length, int element);

Abstraction

Une autre utilité importante des prédicats est de définir l’état logique de nos structures quand les programmes se complexifient. Nos structures doivent généralement respecter un invariant (encore) que chaque fonction de manipulation devra maintenir pour assurer que la structure sera toujours utilisable et qu’aucune fonction ne commettra de bavure.

Cela permet notamment de faciliter la lecture des spécifications. Par exemple, nous pourrions poser les spécifications nécessaires à la sûreté d’une pile de taille limitée. Et cela donnerait quelque chose comme :

struct stack_int{
  size_t top;
  int    data[MAX_SIZE];
};

/*@
  predicate valid_stack_int(struct stack_int* s) = // à définir ;
  predicate empty_stack_int(struct stack_int* s) = // à définir ;
  predicate full_stack_int(struct stack_int* s) =  // à définir ;
*/

/*@
  requires \valid(s);
  assigns *s;
  ensures valid_stack_int(s) && empty_stack_int(s);
*/
void initialize(struct stack_int* s);

/*@
  requires valid_stack_int(s) && !full_stack_int(s);
  assigns  *s;
  ensures valid_stack_int(s);
*/
void push(struct stack_int* s, int value);

/*@
  requires valid_stack_int(s) && !empty_stack_int(s);
  assigns \nothing;
*/
int  top(struct stack_int* s);

/*@
  requires valid_stack_int(s) && !empty_stack_int(s);
  assigns *s;
  ensures valid_stack_int(s);
*/
void pop(struct stack_int* s);

/*@
  requires valid_stack_int(s);
  assigns \nothing;
  ensures \result == 1 <==> empty_stack_int(s);
*/
int  is_empty(stack_int_t s);


/*@
  requires valid_stack_int(s);
  assigns \nothing;
  ensures \result == 1 <==> full_stack_int(s);
*/
int  is_full(stack_int_t s);

(Notons qu’ici, nous ne fournissons pas la définition des prédicats car ce n’est pas l’objet de cet exemple. Le lecteur pourra considérer ceci comme un exercice.)

Ici, la spécification n’exprime pas de propriétés fonctionnelles. Par exemple, rien ne nous spécifie que lorsque nous faisons un push d’une valeur puis que nous demandons top, nous auront effectivement cette valeur. Mais elle nous donne déjà tout ce dont nous avons besoin pour produire un code où, à défaut d’avoir exactement les résultats que nous attendons (des comportements tels que « si j’empile une valeur $v$, l’appel à top renvoie la valeur $v$ », par exemple), nous pouvons au moins garantir que nous n’avons pas d’erreur d’exécution (à condition de poser une spécification correcte pour nos prédicats et de prouver les fonctions d’utilisation de la structure).

Exercices

Les jours du mois

Reprendre la solution de l’exercice des jours du mois de la section sur la modularité du WP, écrire un prédicat pour exprimer qu’une année est bissextile et modifier le contrat de façon à l’utiliser.

Caractères alpha-numériques

Reprendre la solution de l’exercice à propos des caractères alpha-numériques de la section sur la modularité du WP. Écrire un prédicat pour exprimer qu’un caractère est une majuscule, puis faire de même pour les minuscules et les chiffres. Adapter les contrats des différentes fonctions en les utilisant.

Maximum de 3 valeurs

La fonction suivante retourne le maximum de 3 valeurs d’entrée :

int max_of(int* a, int* b, int* c){
  if(*a >= *b && *a >= *c) return *a ;
  if(*b >= *a && *b >= *c) return *b ;
  return *c ;
}

Écrire un prédicat qui exprime qu’une valeur est l’une de trois valeurs pointées à un état mémoire donné :

/*@
  predicate one_of{L}(int value, int *a, int *b, int *c) =
  // ...
*/

Utiliser la notation ensembliste. Écrire un contrat pour la fonction et prouver qu’elle le vérifie.

Recherche dichotomique

Reprendre la solution de l’exercice de la section sur les boucles à propos de la recherche dichotomique utilisant des indices non-signés. Écrire un prédicat qui exprime qu’une plage de valeur est triée entre begin et end (exclu). Écrire une surcharge de ce prédicat pour rendre begin optionnel avec une valeur par défaut à $0$. Écrire un prédicat qui vérifie si un élément est dans un tableau pour des indices compris entre begin et end (exclu), à nouveau, écrire une surcharge qui rend la première borne optionnelle.

Utiliser ces prédicats pour simplifier le contrat de la fonction. Notons que les clauses assumes des deux comportements devraient être modifiées.

Chercher et remplacer

Reprendre l’exemple de la section sur les boucles, à propos de la fonction « chercher et remplacer ». Écrire des prédicats qui exprime qu’une plage de valeurs dans un tableau pour des indices compris entre begin et end (exclu), les valeurs :

• restent inchangées entre deux états mémoire,
• sont remplacées par une valeur si elles sont égales à une valeur donnée, sinon sont laissées inchangées.

Surcharger les deux prédicats de manière à rendre la première borne optionnelle. Utiliser les prédicats obtenus pour simplifier le contrat et l’invariant de boucle de la fonction.

Les fonctions logiques nous permettent de décrire des fonctions mathématiques qui contrairement aux prédicats nous permettent de renvoyer différents types. Elles ne seront utilisables que dans les spécifications. Cela nous permet d’une part, de les factoriser, et d’autre part de définir des opérations sur les types integer et real qui ne peuvent pas déborder contrairement aux types machines.

Comme les prédicats, elles peuvent recevoir divers labels et valeurs en paramètre.

Syntaxe

Pour déclarer une fonction logique, l’écriture est la suivante :

/*@
  logic type_retour ma_fonction{ Lbl0, ..., LblN }( type0 arg0, ..., typeN argN ) =
    formule mettant en jeu les arguments ;
*/

Nous pouvons par exemple décrire une fonction affine générale du côté de la logique :

/*@
  logic integer ax_b(integer a, integer x, integer b) =
    a * x + b;
*/

Elle peut nous servir à prouver le code de la fonction suivante :

/*@ 
  assigns \nothing ;
  ensures \result == ax_b(3,x,4); 
*/
int function(int x){
  return 3*x + 4;
}

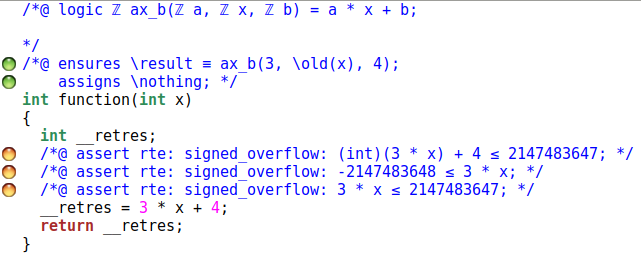
Le code est bien prouvé mais les contrôles d'overflow, eux, ne le sont pas. Nous pouvons ajouter la contrainte en précondition que le calcul doit entrer dans les bornes d’un entier :

/*@
  requires INT_MIN <= ax_b(3, x, 4) <= INT_MAX;
  assigns \nothing ;
  ensures \result == ax_b(3,x,4);
*/
int function(int x){
  return 3*x + 4;
}

Certains contrôles de débordement ne sont pas encore prouvés. En effet, tandis que la borne fournie pour x par notre fonction logique est définie pour le calcul complet, elle ne nous dit rien à propos des calculs intermédiaires. Par exemple ici, le fait 3 * x + 4 ne soit pas inférieur à INT_MIN ne nous garantit pas que c’est aussi le cas pour 3 * x. Nous pouvons imaginer deux manières différentes de résoudre le problème, ce choix doit être guidé par les besoins du projet.

Soit nous pouvons augmenter les restrictions sur l’entrée :

/*@
  requires INT_MIN <= 3*x ;
  requires INT_MIN <= ax_b(3, x, 4) <= INT_MAX;
  assigns \nothing ;
  ensures \result == ax_b(3,x,4); 
*/
int restricted(int x){
  return 3*x + 4;
}

Soit nous pouvons modifier le code de manière à corriger le risque de débordement :

/*@
  requires INT_MIN <= ax_b(3, x, 4) <= INT_MAX;
  assigns \nothing;
  ensures \result == ax_b(3,x,4);
*/
int function_modified(int x){
  if(x > 0)
    return 3 * x + 4;
  else
    return 3 * (x + 2) - 2;
}

Notons que comme dans la spécification, les calculs sont effectués à l’aide d’entiers mathématiques, nous n’avons pas à nous préoccuper d’un quelconque risque de débordement lorsque nous utilisons la fonction logique ax_b :

void mathematical_example(void){
  //@ assert ax_b(42, INT_MAX, 1) < ax_b(70, INT_MAX, 1) ;
}

est correctement déchargé par WP, qui ne génère aucune alarme liée aux débordements :

Récursivité et limites

Les fonctions logiques peuvent être définies récursivement. Cependant, une telle définition montrera très rapidement ses limites pour la preuve. En effet, pendant les manipulations des prouveurs automatiques sur les propriétés logiques, si l’usage d’une telle fonction est présente, elle devra être évaluée. Or, les prouveurs ne sont pas conçus pour faire ce genre d’évaluation, qui se révélera donc généralement très coûteuse et produisant des temps de preuve trop longs menant à des timeouts.

Exemple concret, nous pouvons définir la fonction factorielle, dans la logique et en C :

/*@
  logic integer factorial(integer n) = (n <= 0) ? 1 : n * factorial(n-1);
*/

/*@ 
  assigns \nothing ;
  ensures \result == factorial(n) ; 
*/
int facto(int n){
  if(n < 2) return 1 ;

  int res = 1 ;
  /*@
    loop invariant 2 <= i <= n+1 ;
    loop invariant res == factorial(i-1) ;
    loop assigns i, res ;
    loop variant n - i ;
  */
  for(int i = 2 ; i <= n ; i++){
    res = res * i ;
  }
  return res ;
}

Sans contrôle de borne, cette fonction se prouve rapidement. Si nous ajoutons le contrôle des RTE, nous voyons qu’il y a un risque de débordement arithmétique sur la multiplication.

Sur le type int, le maximum que nous pouvons calculer est la factorielle de 12. Au-delà, cela produit un dépassement. Nous pouvons donc ajouter cette précondition :

/*@
  logic integer factorial(integer n) = (n <= 0) ? 1 : n * factorial(n-1);
*/

/*@ 
  requires n <= 12 ;
  assigns \nothing ;
  ensures \result == factorial(n) ; 
*/
int facto(int n){
  if(n < 2) return 1 ;

  int res = 1 ;
  /*@
    loop invariant 2 <= i <= n+1 ;
    loop invariant res == factorial(i-1) ;
    loop assigns i, res ;
    loop variant n - i ;
  */
  for(int i = 2 ; i <= n ; i++){
    res = res * i ;
  }
  return res ;
}

Si nous demandons la preuve avec cette entrée, Alt-ergo échouera pratiquement à coup sûr. En revanche, le prouveur Z3 produit la preuve en moins d’une seconde. Parce que dans ce cas précis, les heuristiques de Z3 considèrent que c’est une bonne idée de passer un peu plus de temps sur l’évaluation de la fonction.

Les fonctions logiques peuvent donc être définies récursivement mais sans astuces supplémentaires, nous venons vite nous heurter au fait que les prouveurs vont au choix devoir faire de l’évaluation, ou encore « raisonner » par induction, deux tâches pour lesquelles ils ne sont pas du tout faits, ce qui limite nos possibilités de preuve. Nous verrons plus tard dans ce tutoriel comment éviter cette limitation.

Exercices

Distance

Spécifier et prouver le programme suivant:

int distance(int a, int b){
  if(a < b) return b - a ;
  else return a - b ;
}

Pour cela, définir deux fonctions logiques abs et distance. Utiliser ces fonctions pour écrire la spécification de la fonction.

Carré

Écrire le corps de la fonction square. Spécifier et prouver le programme. Utiliser une fonction logique square.

int abs(int x){
  return (x < 0) ? -x : x ;
}

unsigned square(int x){
  
}

Attention aux types des différentes variables, de telle manière à ne pas sur-contraindre les entrées de la fonction. De plus, pour vérifier l’absence d’erreurs à l’exécution, utiliser les options -warn-unsigned-overflow et -warn-unsigned-downcast.

Iota

Voici une implémentation possible de la fonction iota :

#include <limits.h>
#include <stddef.h>

void iota(int* array, size_t len, int value){
  if(len){
    array[0] = value ;

    for(size_t i = 1 ; i < len ; i++){
      array[i] = array[i-1]+1 ;
    }
  }
}

Écrire une fonction logique qui retourne sa valeur d’entrée incrémentée de 1. Prouver qu’après l’exécution de iota, la première valeur du tableau est celle reçue en entrée et que chaque valeur du tableau correspond à la valeur précédente plus 1 (en utilisant la fonction logique définie).

Addition sur un vecteur

Dans le programme suivant, la fonction vec_add ajoute le second vecteur reçu en entrée dans le premier. Écrire un contrat pour la fonction show_the_difference qui exprime pour chaque valeur du vecteur v1 la différence entre la pré et la postcondition. Pour cela, définir une fonction logique diff qui retourne la différence de valeur à une position mémoire entre un label L1 et la valeur au label L2.

#include <stddef.h>
#include <limits.h>

/*@
  predicate unchanged{L1, L2}(int* ptr, integer a, integer b) =
    \forall integer i ; a <= i < b ==> \at(ptr[i], L1) == \at(ptr[i], L2) ;
*/

/*@
  requires \valid(v1 + (0 .. len-1));
  requires \valid_read(v2 + (0 .. len-1));
  requires \separated(v1 + (0 .. len-1), v2 + (0 .. len-1));
  requires 
    \forall integer i ; 0 <= i < len ==> INT_MIN <= v1[i]+v2[i] <= INT_MAX ;
  assigns v1[0 .. len-1];
  
  ensures 
    \forall integer i ; 0 <= i < len ==> v1[i] == \old(v1[i]) + v2[i] ;
  ensures 
    \forall integer i ; 0 <= i < len ==> v2[i] == \old(v2[i]) ;
*/
void vec_add(int* v1, const int* v2, size_t len){
  /*@
    loop invariant 0 <= i <= len ;
    loop invariant 
      \forall integer j ; 0 <= j < i ==> v1[j] == \at(v1[j], Pre) + v2[j] ;
    loop invariant unchanged{Pre, Here}(v1, i, len) ;
    loop assigns i, v1[0 .. len-1] ;
    loop variant len-i ;
  */
  for(size_t i = 0 ; i < len ; ++i){
    v1[i] += v2[i] ;
  }
}

void show_the_difference(int* v1, const int* v2, size_t len){
  vec_add(v1, v2, len);
}

Ré-exprimer le prédicat unchanged en utilisant la fonction logique.

La somme des N premiers entiers

La fonction suivante calcule la somme des N premiers entiers. Écrire une fonction logique récursive qui retourne la somme des N premiers entiers et écrire la la spécification de la fonction C effectuant ce calcul en spécifiant qu’elle retourne la même valeur que celle fournie par la fonction logique.

int sum_n(int n){
  if(n < 1) return 0 ;

  int res = 0 ;
  for(int i = 1 ; i <= n ; i++){
    res += i ;
  }
  return res ;
}

Essayer de vérifier l’absence d’erreurs à l’exécution. Le débordement entier n’est pas si simple à régler. Cependant, écrire une précondition qui devrait être suffisante pour cela (rappel: la somme des N premiers entiers peut être exprimée avec une formule très simple …). Cela ne sera sûrement pas suffisant pour arriver au bout de la preuve, mais nous réglerons cela dans la prochaine section.

Les lemmes sont des propriétés générales à propos des prédicats ou encore des fonctions. Une fois ces propriétés exprimées, la preuve peut être réalisée en isolation du reste de la preuve du programme, en utilisant des prouveurs automatiques ou (plus souvent) des prouveurs interactifs. Une fois la preuve réalisée, la propriété énoncée peut être utilisée directement par les prouveurs automatiques sans que cela ne nécessite d’en réaliser la preuve à nouveau. Par exemple, si nous énonçons un lemme $L$ qui dit que $P \Rightarrow Q$, et dans une autre preuve nous avons besoin de prouver $Q$ alors que nous savons déjà que $P$ est vérifiée, nous pouvons utiliser directement le lemme $L$ pour conclure sans avoir besoin de faire à nouveau le raisonnement complet qui amène de $P$ à $Q$.

Dans la section précédente, nous avons dit que les fonctions récursives logiques peuvent rendre les preuves plus difficiles pour les solveurs SMT. Dans un tel cas, les lemmes peuvent nous aider. Nous pouvons écrire nous même les preuves qui nécessitent de raisonner par induction pour certaines propriétés que nous énonçons comme des lemmes, et ces lemmes peuvent ensuite être utilisés efficacement par les prouveurs pour effectuer les autres preuves à propos du programme.

Syntaxe

Une nouvelle fois, nous les introduisons à l’aide d’annotations ACSL. La syntaxe utilisée est la suivante :

/*@
  lemma name_of_the_lemma { Label0, ..., LabelN }:
    property ;
*/

Cette fois les propriétés que nous voulons exprimer ne dépendent pas de paramètres reçus (hors de nos labels bien sûr). Ces propriétés seront donc exprimées sur des variables quantifiées. Par exemple, nous pouvons poser ce lemme qui est vrai, même s’il est trivial :

/*@
  lemma lt_plus_lt:
    \forall integer i, j ; i < j ==> i+1 < j+1;
*/

Cette preuve peut être effectuée en utilisant WP. La propriété est bien sûr trivialement prouvée par Qed.

Exemple : propriété fonction affine

Nous pouvons par exemple reprendre nos fonctions affines et exprimer quelques propriétés intéressantes à leur sujet :

/* @
  lemma ax_b_monotonic_neg:
    \forall integer a, b, i, j ;
      a <  0 ==> i <= j ==> ax_b(a, i, b) >= ax_b(a, j, b);
  lemma ax_b_monotonic_pos:
    \forall integer a, b, i, j ;
      a >  0 ==> i <= j ==> ax_b(a, i, b) <= ax_b(a, j, b);
  lemma ax_b_monotonic_nul:
    \forall integer a, b, i, j ;
      a == 0 ==> ax_b(a, i, b) == ax_b(a, j, b);
*/

Pour ces preuves, il est fort possible qu’Alt-ergo ne parvienne pas à les décharger. Dans ce cas, le prouveur Z3 devrait, lui, y arriver. Nous pouvons ensuite construire cet exemple de code :

/*@
  requires INT_MIN <= a*x <= INT_MAX ;
  requires INT_MIN <= ax_b(a,x,4) <= INT_MAX ;
  assigns \nothing ;
  ensures \result == ax_b(a,x,4); 
*/
int function(int a, int x){
  return a*x + 4;
}

/*@ 
  requires INT_MIN <= a*x <= INT_MAX ;
  requires INT_MIN <= a*y <= INT_MAX ;
  requires a > 0;
  requires INT_MIN <= ax_b(a,x,4) <= INT_MAX ;
  requires INT_MIN <= ax_b(a,y,4) <= INT_MAX ;
  assigns \nothing ;
*/
void foo(int a, int x, int y){
  int fmin, fmax;
  if(x < y){
    fmin = function(a,x);
    fmax = function(a,y);
  } else {
    fmin = function(a,y);
    fmax = function(a,x);
  }
  //@assert fmin <= fmax;
}

Si nous ne renseignons pas les lemmes mentionnés plus tôt, il y a peu de chances qu’Alt-ergo réussisse à produire la preuve que fmin est inférieur à fmax. Avec ces lemmes présents en revanche, il y parvient sans problème car cette propriété est une simple instance du lemme ax_b_monotonic_pos, la preuve étant ainsi triviale car notre lemme nous énonce cette propriété comme étant vraie. Notons que sur cette version généralisée, Z3 sera probablement plus efficace pour prouver l’absence d’erreurs à l’exécution.

Exemple: tableaux et labels

Plus tard dans ce tutoriel, nous verrons certains types de définitions à propos desquels il est parfois difficile de raisonner pour les solveurs SMT quand des modifications ont lieu en mémoire. Par conséquent, nous aurons souvent besoin de lemmes pour indiquer les relations qui existent à propos du contenu de la mémoire entre deux labels.

Pour le moment, illustrons cela avec un exemple simple. Considérons les deux prédicats suivant :

/*@ 
  predicate sorted(int* array, integer begin, integer end) =
    \forall integer i, j ; begin <= i <= j < end ==> array[i] <= array[j] ;
  predicate unchanged{L1, L2}(int *array, integer begin, integer end) =
    \forall integer i ; begin <= i < end ==> 
      \at(array[i], L1) == \at(array[i], L2) ;
*/

Nous pourrions par exemple vouloir énoncer que lorsqu’un tableau est trié, et que la mémoire est modifiée (créant donc un nouvel état mémoire), mais que le contenu du tableau reste inchangé, alors le tableau est toujours trié. Cela peut être réalisé avec le lemme suivant :

/*@
  lemma unchanged_sorted{L1, L2}:
    \forall int* array, integer b, integer e ;
      sorted{L1}(array, b, e) ==>
      unchanged{L1, L2}(array, b, e) ==> 
        sorted{L2}(array, b, e) ;
*/

Nous énonçons ce lemme pour deux labels L1 et L2, et exprimons que pour toute plage de valeurs dans un tableau, si elle est triée au label L1, et reste inchangée depuis L1 vers L2, alors elle reste triée au label L2.

Notons qu’ici, cette propriété est facilement prouvée par les prouveurs SMT. Nous verrons plus tard des exemples pour lesquels il n’est pas si simple d’obtenir une preuve.

Exercices

Propriété de la multiplication

Écrire un lemme qui énonce que pour trois entiers $x$, $y$ et $z$, si $x$ est plus grand ou égal à $0$, si $z$ est plus grand ou égal à $y$, alors $x * z$ est plus grand ou égal à $x * y$.

Ce lemme ne sera probablement pas prouvé par les solveurs SMT. En revanche, en demandant une preuve avec Coq, la tactique par défaut devrait la décharger automatiquement.

Localement trié vers globalement trié

Le programme suivant contient une fonction qui demande à ce qu’un tableau soit trié au sens que chaque élément soit plus petit ou égal à l’élément qui le suit puis appelle la fonction de recherche dichotomique.

/*@
  predicate element_level_sorted(int* array, integer fst, integer end) =
    \forall integer i ; fst <= i < end-1 ==> array[i] <= array[i+1] ;
*/
/*@
  //lemma element_level_sorted_implies_sorted:
  // ...
*/

/*@
  requires \valid_read(arr + (0 .. len-1));
  requires element_level_sorted(arr, 0, len) ;
  requires in_array(value, arr, len);
  assigns \nothing ;
  ensures 0 <= \result < len ;
  ensures arr[\result] == value ;
*/
unsigned bsearch_callee(int* arr, size_t len, int value){
  return bsearch(arr, len, value);
}

Pour cet exercice, reprendre la solution de l’exercice de la section sur les prédicats à propos de la recherche dichotomique. La précondition de cette recherche peut sembler plus forte que celle reçue par la précondition de bsearch_callee. La première demande chaque paire d’éléments d’être ordonnée, la seconde simplement que chaque élément soit inférieur à celui qui le suit. Cependant, la seconde implique la première. Écrire un lemme qui énonce que si element_level_sorted est vraie pour un tableau, sorted est vraie aussi. Ce lemme ne sera probablement pas prouvé par un solveur SMT, toutes les autres propriétés devraient être prouvées automatiquement.

Une solution et la preuve Coq du lemme sont disponibles sur le GitHub de ce tutoriel.

Somme des N premiers entiers

Reprendre la solution de l’exercice de la section précédente à propos de la somme des N premiers entiers. Écrire un lemme qui énonce que la valeur calculée par la fonction logique récursive qui permet la spécification de la somme des N premiers entiers est $n*(n+1)/2$. Ce lemme ne sera pas prouvé par un solveur SMT.

Une solution et la preuve Coq du lemme sont disponibles sur le GitHub de ce tutoriel.

Transitivité d’un glissement d’éléments

Le programme suivant est composé de deux fonctions. La première est shift_array et permet de faire glisser des éléments dans un tableau d’un certain nombre de cellules (nommé shift). La seconde effectue deux glissements successifs des éléments d’un même tableau.

#include <stddef.h>
#include <limits.h>

/*@
  predicate shifted_cell{L1, L2}(int* p, integer shift) =
    \at(p[0], L1) == \at(p[shift], L2) ;

  // predicate shifted{L1, L2}(int* arr, integer fst, integer last, integer shift) =
  // ...
  // predicate unchanged{L1, L2}(int *a, integer begin, integer end) =
  // ...
  // lemma shift_ptr{...}:
  // ...
  // lemma shift_transivity{...}:
  // ...
*/

void shift_array(int* array, size_t len, size_t shift){
  for(size_t i = len ; i > 0 ; --i){
    array[i+shift-1] = array[i-1] ;
  }
}

/*@
  requires \valid(array+(0 .. len+s1+s2-1)) ;
  requires s1+s2 + len <= UINT_MAX ;
  assigns array[s1 .. s1+s2+len-1];
  ensures shifted{Pre, Post}(array, 0, len, s1+s2) ;
*/
void double_shift(int* array, size_t len, size_t s1, size_t s2){
  shift_array(array, len, s1) ;
  shift_array(array+s1, len, s2) ;
}

Compléter les prédicats shifted et unchanged. Le prédicat shifted doit utiliser shifted_cell. Le prédicat unchanged doit utiliser shifted. Compléter le contrat de la fonction shift_array et prouver sa correction avec WP.

Exprimer deux lemmes à propos de la propriété shifted.

Le premier, nommé shift_ptr, doit énoncer que déplacer une plage de valeur fst+s1 à last+s1 dans un tableau array d’un décalage s2 est équivalent à déplacer une plage de valeurs fst à last pour la position mémoire array+s1 avec un décalage s2.

Le second doit énoncer que quand les éléments d’un tableau sont déplacés une première fois avec un décalage s1 puis une seconde fois avec un décalage s2, alors le déplacement final correspond à un décalage avec un déplacement s1+s2.

Le lemme shift_ptr ne sera probablement pas prouvé par un solveur SMT. Nous fournissons une solution et la preuve Coq de ce lemme sur le GitHub de ce tutoriel. Les propriétés restantes doivent être prouvées automatiquement.

Déplacement d’une plage triée

Le programme suivant est composé de deux fonctions. La fonction shift_and_search déplace les éléments d’un tableau puis effectue une recherche dichotomique.

/*@
  predicate shifted_cell{L1, L2}(int* p, integer shift) =
    \at(p[0], L1) == \at(p[shift], L2) ;
*/

size_t bsearch(int* arr, size_t beg, size_t end, int value);

/*@
  // lemma shifted_still_sorted{...}:
  // ...
*/

/*@
  requires sorted(array, 0, len) ;
  requires \valid(array + (0 .. len));
  requires in_array(value, array, 0, len) ;
  assigns array[1 .. len] ;
  
  ensures 1 <= \result <= len ;
*/
unsigned shift_and_search(int* array, size_t len, int value){
  shift_array(array, len, 1);
  return bsearch(array, 1, len+1, value);
}

Reprendre la solution de la recherche dichotomique de l’exercice de la section sur les prédicats. Modifier cette recherche et sa spécification de façon à ce que la fonction permette de chercher dans toute plage triée de valeurs. La preuve doit toujours fonctionner.

Reprendre également la fonction prouvée shift_array de l’exercice précédent.

Compléter le contrat de la fonction shift_and_search. La précondition qui demande à ce que le tableau soit trié avant la recherche ne sera pas validée, ni la postcondition de l’appelant. Compléter le lemme shifted_still_sorted qui doit énoncer que si une plage de valeur est triée à un label, puis déplacée, alors elle reste triée. Ensuite, compléter le lemme in_array_shifted qui doit énoncer que si une valeur est dans une plage de valeur, alors lorsque cette plage est déplacée, la valeur est toujours dans la nouvelle plage obtenue. La postcondition de l’appelant devrait maintenant être prouvée.

Ces lemmes ne seront probablement pas prouvés par un solveur SMT. Une solution et les preuves Coq sont disponibles sur le GitHub de ce tutoriel.