Contrats de fonctions

Le principe d’un contrat de fonction est de poser les conditions selon lesquelles la fonction s’exécutera. On distinguera deux parties :

• la précondition, c’est-à-dire ce que doit respecter le code appelant à propos des variables passées en paramètres et de l’état de la mémoire globale pour que la fonction s’exécute correctement ;
• la postcondition, c’est-à-dire ce que s’engage à respecter la fonction en retour à propos de l’état de la mémoire et de la valeur de retour.

Ces propriétés sont exprimées en langage ACSL, dont la syntaxe est relativement simple pour qui a déjà fait du C, puisqu’elle reprend la syntaxe des expressions booléennes du C. Cependant, elle ajoute également :

• certaines constructions et connecteurs logiques qui ne sont pas présents originellement en C pour faciliter l’écriture ;
• des prédicats pré-implémentés pour exprimer des propriétés souvent utiles en C (par exemple, la validité d’un pointeur) ;
• ainsi que des types plus généraux que les types primitifs du C, typiquement les types entiers ou réels.

Nous introduirons au fil du tutoriel les notations présentes dans le langage ACSL.

Les spécifications ACSL sont introduites dans nos codes source par l’intermédiaire d’annotations placées dans des commentaires. Syntaxiquement, un contrat de fonction est intégré dans les sources de la manière suivante :

/*@
  //contrat
*/
void foo(int bar){

}

Notons bien le @ à la suite du début du bloc de commentaire, c’est lui qui fait que ce bloc devient un bloc d’annotations pour Frama-C et pas un simple bloc de commentaires à ignorer.

Maintenant, regardons comment sont exprimés les contrats, à commencer par la postcondition, puisque c’est ce que nous attendons en priorité de notre programme (nous nous intéresserons ensuite aux préconditions).

Postcondition

La postcondition d’une fonction est précisée avec la clause ensures. Nous travaillerons avec la fonction suivante qui donne la valeur absolue d’un entier reçu en entrée. Une de ses postconditions est que le résultat (que nous notons avec le mot-clé \result) est supérieur ou égal à 0.

/*@
  ensures \result >= 0;
*/
int abs(int val){
  if(val < 0) return -val;
  return val;
}

(Notons le ; à la fin de la ligne de spécification comme en C).

Mais ce n’est pas tout, il faut également spécifier le comportement général attendu d’une fonction renvoyant la valeur absolue. À savoir : si la valeur est positive ou nulle, la fonction renvoie la même valeur, sinon elle renvoie l’opposé de la valeur.

Nous pouvons spécifier plusieurs postconditions, soit en les composants avec un && comme en C, soit en introduisant une nouvelle clause ensures, comme illustré ci-dessous.

/*@
  ensures \result >= 0;
  ensures (val >= 0 ==> \result == val ) && 
          (val <  0 ==> \result == -val);
*/
int abs(int val){
  if(val < 0) return -val;
  return val;
}

Cette spécification est l’opportunité de présenter un connecteur logique très utile que propose ACSL mais qui n’est pas présent en C : l’implication $A \Rightarrow B$, que l’on écrit en ACSL A ==> B. La table de vérité de l’implication est la suivante :

Ce qui veut dire qu’une implication $A \Rightarrow B$ est vraie dans deux cas : soit $A$ est fausse (et dans ce cas, il ne faut pas se préoccuper de $B$), soit $A$ est vraie et alors $B$ doit être vraie aussi. Notons que cela signifie que $A \Rightarrow B$ est équivalente à $\neg A \vee B$. L’idée étant finalement « je veux savoir si dans le cas où $A$ est vrai, $B$ l’est aussi. Si $A$ est faux, je considère que l’ensemble est vrai ». Par exemple, « s’il pleut, je veux vérifier que j’ai un parapluie, s’il ne pleut pas, ce n’est pas un problème de savoir si j’en ai un ou pas, tout va bien ».

Sa cousine l’équivalence $A \Leftrightarrow B$ (écrite A <==> B en ACSL) est plus forte. C’est la conjonction de l’implication dans les deux sens : $(A \Rightarrow B) \wedge (B \Rightarrow A)$. Cette formule n’est vraie que dans deux cas : $A$ et $B$ sont vraies toutes les deux, ou fausses toutes les deux (c’est donc la négation du ou-exclusif). Pour continuer avec notre petit exemple, « je ne veux plus seulement savoir si j’ai un parapluie quand il pleut, je veux être sûr de n’en avoir que dans le cas où il pleut ».

Revenons à notre spécification. Quand nos fichiers commencent à être longs et contenir beaucoup de spécifications, il peut être commode de nommer les propriétés que nous souhaitons vérifier. Pour cela, nous indiquons un nom (les espaces ne sont pas autorisées) suivi de : avant de mettre effectivement la propriété, il est possible de mettre plusieurs « étages » de noms pour catégoriser nos propriétés. Par exemple, nous pouvons écrire ceci :

/*@
  ensures positive_value: function_result: \result >= 0;
  ensures (val >= 0 ==> \result == val) && 
          (val < 0 ==> \result == -val);
*/
int abs(int val){
  if(val < 0) return -val;
  return val;
}

Dans une large part du tutoriel, nous ne nommerons pas les éléments que nous tenterons de prouver, les propriétés seront généralement relativement simples et peu nombreuses, les noms n’apporteraient pas beaucoup d’information.

Nous pouvons copier/coller la fonction abs et sa spécification dans un fichier abs.c et regarder avec Frama-C si l’implémentation est conforme à la spécification.

Pour cela, il faut lancer l’interface graphique de Frama-C (il est également possible de se passer de l’interface graphique, cela ne sera pas présenté dans ce tutoriel) soit par cette commande :

$ frama-c-gui

Soit en l’ouvrant depuis l’environnement graphique.

Il est ensuite possible de cliquer sur le bouton « Create a new session from existing C files », les fichiers à analyser peuvent être sélectionnés par double-clic, OK terminant la sélection. Par la suite, l’ajout d’autres fichiers à la session s’effectue en cliquant sur Files > Source Files.

À noter également qu’il est possible d’ouvrir directement le(s) fichier(s) depuis la ligne de commande en le(s) passant en argument(s) de frama-c-gui.

$ frama-c-gui abs.c

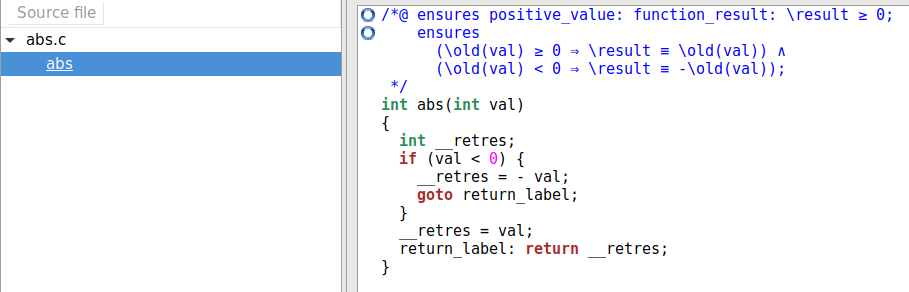
La fenêtre de Frama-C s’ouvre, dans le volet correspondant aux fichiers et aux fonctions, nous pouvons sélectionner la fonction abs. Pour chaque ligne ensures, il y a un cercle bleu dans la marge. Ces cercles indiquent qu’aucune vérification n’a été tentée pour ces lignes.

Nous demandons de vérifier que le code répond à la spécification en faisant un clic droit sur le nom de la fonction et « Prove function annotations by WP » :

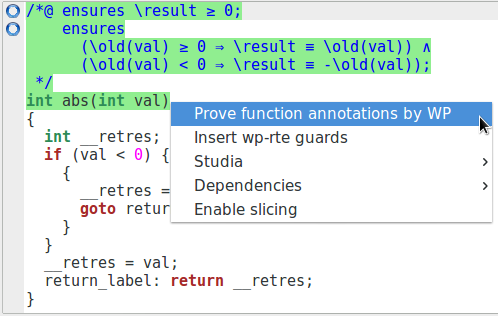
Nous pouvons voir que les cercles bleus deviennent des pastilles vertes, indiquant que la spécification est bien assurée par le programme. Il est possible de prouver les propriétés une à une en cliquant-droit sur celles-ci et pas sur le nom de la fonction.

Mais le code est-il vraiment sans erreur pour autant ? WP nous permet de nous assurer que le code répond à la spécification, mais il ne fait pas de contrôle d’erreur à l’exécution (runtime error, abrégé RTE) si nous le demandons pas. Un autre plugin de Frama-C, appelé sobrement RTE, peut être utilisé pour générer des annotations ACSL qui peuvent ensuite être vérifiées par d’autres plugins. Son but est d’ajouter des contrôles dans le programme pour les erreurs d’exécutions possibles (débordements d’entiers, déréférencements de pointeurs invalides, division par 0, etc).

Pour activer ce contrôle, nous devons activer l’option dans la configuration de WP. Pour cela, il faut d’abord cliquer sur le bouton de configuration des plugins :

Et ensuite cocher l’option -wp-rte dans les options liées à WP :

Il est également possible de demander à WP d’ajouter ces contrôles par un clic droit sur le nom de la fonction puis « Insert wp-rte guards ».

Enfin, nous relançons la vérification (nous pouvons également cliquer sur le bouton « Reparse » de la barre d’outils, cela aura pour effet de supprimer les preuves déjà effectuées).

Nous voyons alors que WP échoue à prouver l’impossibilité de débordement arithmétique sur le calcul de -val. Et c’est bien normal parce que -INT_MIN ($-2^{31}$) > INT_MAX ($2^{31}-1$).

Ici, nous pouvons voir un autre type d’annotation ACSL. La ligne //@ assert propriete ; nous permet de demander la vérification d’une propriété à un point particulier du programme. Ici, l’outil l’a insérée pour nous, car il faut vérifier que le -val ne provoque pas de débordement, mais il est également possible d’en ajouter manuellement dans un code.

Comme le montre cette capture d’écran, nous avons deux nouveaux codes couleur pour les pastilles : vert + marron et orange.

La couleur vert + marron nous indique que la preuve a été effectuée mais qu’elle dépend potentiellement de propriétés pour lesquelles ce n’est pas le cas.

Si la preuve n’a pas été recommencée intégralement par rapport à la preuve précédente, ces pastilles ont dû rester vertes, car les preuves associées ont été réalisées avant l’introduction de la propriété nous assurant l’absence d’erreur d’exécution, et ne se sont donc pas reposées sur la connaissance de cette propriété puisqu’elle n’existait pas.

En effet, lorsque WP transmet une obligation de preuve à un prouveur automatique, il transmet deux types de propriétés : $G$, le but, la propriété que l’on cherche à prouver, et $S_1$ … $S_n$ les diverses suppositions que l’on peut faire à propos de l’état du programme au point où l’on cherche à vérifier $G$. Cependant, il ne reçoit pas, en retour, quelles propriétés ont été utilisées par le prouveur pour valider $G$. Donc si $S_3$ fait partie des suppositions, et si WP n’a pas réussi à obtenir une preuve de $S_3$, il indique que $G$ est vraie, mais en supposant que $S_3$ est vraie, pour laquelle nous n’avons actuellement pas établi de preuve.

La couleur orange nous signale qu’aucun prouveur n’a pu déterminer si la propriété est vérifiable. Les deux raisons peuvent être :

• qu’il n’a pas assez d’information pour le déterminer ;
• que malgré toutes ses recherches, il n’a pas pu trouver un résultat à temps. Auquel cas, il rencontre un timeout dont la durée est configurable dans le volet de WP.

Dans le volet inférieur, nous pouvons sélectionner l’onglet « WP Goals », celui-ci nous affiche la liste des obligations de preuve et pour chaque prouveur indique un petit logo si la preuve a été tentée et si elle a été réussie, échouée ou a rencontré un timeout (logo avec les ciseaux). Pour voir la totalité des obligations de preuves, il faut s’assurer que « All Results » est bien sélectionné dans le champ encadré dans la capture.

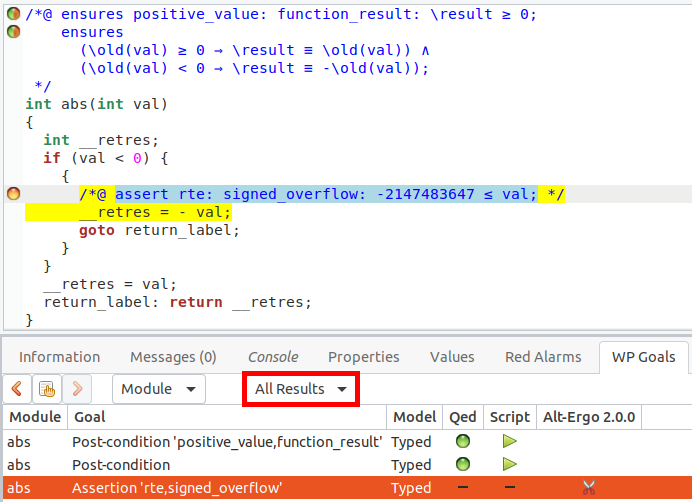
Le tableau est découpé comme suit, en première colonne nous avons le nom de la fonction où se trouve le but à prouver. En seconde colonne nous trouvons le nom du but. Ici par exemple notre postcondition nommée est estampillée « Post-condition 'positive_value,function_result' », nous pouvons d’ailleurs noter que lorsqu’une propriété est sélectionnée dans le tableau, elle est également surlignée dans le code source. Les propriétés anonymes se voient assignées comme nom le type de propriété voulu. En troisième colonne, nous trouvons le modèle mémoire utilisé pour la preuve, (nous n’en parlerons pas dans ce tutoriel). Finalement, les dernières colonnes représentent les différents prouveurs accessibles à WP.

Dans ces prouveurs, le premier élément de la colonne est Qed. Ce n’est pas à proprement parler un prouveur. C’est un outil utilisé par WP pour simplifier les propriétés avant de les envoyer aux prouveurs externes. Ensuite, nous voyons la colonne Script, les scripts fournissent une manière de terminer les preuves à la main lorsque les prouveurs automatiques n’y arrivent pas. Finalement, nous trouvons la colonne Alt-Ergo, qui est un prouveur automatique. Notons que sur la propriété en question des ciseaux sont indiqués, cela veut dire que le prouveur a été stoppé à cause d’un timeout.

En fait, si nous double-cliquons sur la propriété « ne pas déborder » (surlignée en bleu dans la capture précédente), nous pouvons voir ceci (si ce n’est pas le cas, il faut s’assurer que « Raw obligation » est bien sélectionné dans le champ encadré en bleu) :

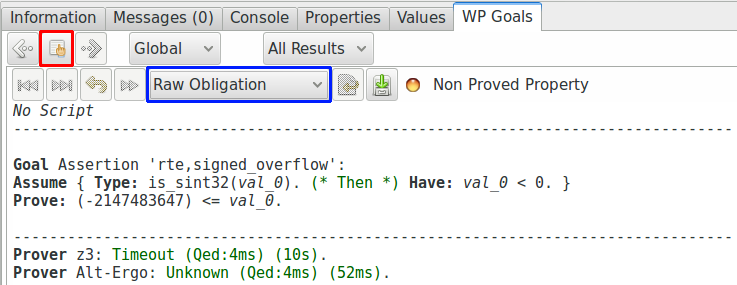
C’est l’obligation de preuve que génère WP par rapport à notre propriété et notre programme, il n’est pas nécessaire de comprendre tout ce qu’il s’y passe, juste d’avoir une idée globale. Elle contient (dans la partie « Assume ») les suppositions que nous avons pu donner et celles que WP a pu déduire des instructions du programme. Elle contient également (dans la partie « Prove ») la propriété que nous souhaitons vérifier.

Que fait WP avec ces éléments ? En fait, il les transforme en une formule logique puis demande aux différents prouveurs s’il est possible de la satisfaire (de trouver pour chaque variable, une valeur qui rend la formule vraie), cela détermine si la propriété est prouvable. Mais avant d’envoyer cette formule aux prouveurs, WP utilise un module qui s’appelle Qed et qui est capable de faire différentes simplifications à son sujet. Parfois, comme dans le cas des autres propriétés de abs, ces simplifications suffisent à déterminer que la propriété est forcément vraie, auquel cas, nous ne faisons pas appel aux prouveurs.

Lorsque les prouveurs automatiques ne parviennent pas à assurer que nos propriétés sont bien vérifiées, il est parfois difficile de comprendre pourquoi. En effet, les prouveurs sont en général incapables de nous répondre autre chose que « oui », « non » ou « inconnu », ils sont incapables d’extraire le « pourquoi » d’un « non » ou d’un « inconnu ». Il existe des outils qui sont capables d’explorer les arbres de preuve pour en extraire ce type d’information, Frama-C n’en possède pas à l’heure actuelle. La lecture des obligations de preuve peut parfois nous aider, mais cela demande un peu d’habitude pour pouvoir les déchiffrer facilement. Finalement, le meilleur moyen de comprendre la raison d’un échec est d’effectuer la preuve de manière interactive avec Coq. En revanche, il faut déjà avoir une certaine habitude de ce langage pour ne pas être perdu devant les obligations de preuve générées par WP, étant donné que celles-ci encodent les éléments de la sémantique de C, ce qui rend le code souvent indigeste.

Si nous retournons dans notre tableau des obligations de preuve (bouton encadré dans la capture d’écran précédente), nous pouvons donc voir que les hypothèses n’ont pas suffi aux prouveurs pour déterminer que la propriété « absence de débordement » est vraie (et nous l’avons dit : c’est normal), il nous faut donc ajouter une hypothèse supplémentaire pour garantir le bon fonctionnement de la fonction : une précondition d’appel.

Précondition

Les préconditions de fonctions sont introduites par la clause requires. De la même manière qu’avec ensures, nous pouvons composer nos expressions logiques et mettre plusieurs préconditions :

/*@
  requires 0 <= a < 100;
  requires b < a;
*/
void foo(int a, int b){
  
}

Les préconditions sont des propriétés sur les entrées (et potentiellement sur des variables globales) qui seront supposées préalablement vraies lors de l’analyse de la fonction. La preuve que celles-ci sont effectivement validées n’interviendra qu’aux points où la fonction est appelée.

Dans ce petit exemple, nous pouvons également noter une petite différence avec le C dans l’écriture des expressions booléennes. Si nous voulons spécifier que a se trouve entre 0 et 100, il n’y a pas besoin d’écrire 0 <= a && a < 100 (c’est-à-dire en composant les deux comparaisons avec un &&). Nous pouvons simplement écrire 0 <= a < 100 et l’outil se chargera de faire la traduction nécessaire.

Si nous revenons à notre exemple de la valeur absolue, pour éviter le débordement arithmétique, il suffit que la valeur de val soit strictement supérieure à INT_MIN pour garantir que le débordement n’arrive pas. Nous l’ajoutons donc comme précondition (à noter : il faut également inclure l’en-tête où INT_MIN est défini) :

#include <limits.h>

/*@
  requires INT_MIN < val;

  ensures \result >= 0;
  ensures (val >= 0 ==> \result == val) && 
          (val < 0 ==> \result == -val);
*/
int abs(int val){
  if(val < 0) return -val;
  return val;
}

Une fois le code source modifié de cette manière, un clic sur « Reparse » et nous lançons à nouveau l’analyse. Cette fois, tout est validé pour WP ; notre implémentation est prouvée :

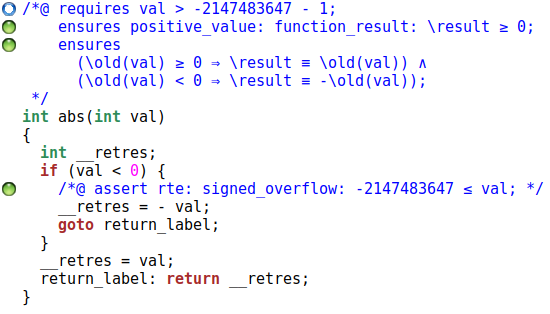
Nous pouvons également vérifier qu’une fonction qui appellerait abs respecte bien la précondition qu’elle impose :

void foo(int a){
   int b = abs(42);
   int c = abs(-42);
   int d = abs(a);       // Faux : "a", vaut peut-être INT_MIN
   int e = abs(INT_MIN); // Faux : le paramètre doit être strictement supérieur à INT_MIN
}

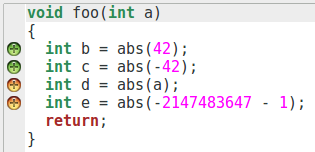
Notons qu’en cliquant sur la pastille à côté de l’appel de fonction, nous pouvons voir la liste des préconditions et voir quelles sont celles qui ne sont pas vérifiées. Ici, nous n’avons qu’une précondition, mais quand il y en a plusieurs, c’est très utile pour pouvoir voir quel est exactement le problème.

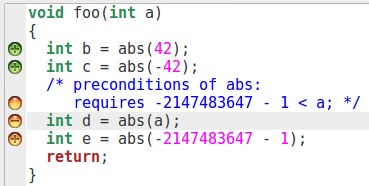
Pour modifier un peu l’exemple, nous pouvons essayer d’inverser les deux dernières lignes. Auquel cas, nous pouvons voir que l’appel abs(a) est validé par WP s’il se trouve après l’appel abs(INT_MIN) ! Pourquoi ?

Il faut bien garder en tête que le principe de la preuve déductive est de nous assurer que si les préconditions sont vérifiées et que le calcul termine alors la postcondition est vérifiée.

Si nous donnons à notre fonction une valeur qui viole explicitement sa précondition, nous pouvons déduire que n’importe quoi peut arriver, incluant obtenir « faux » en postcondition. Plus précisément, ici, après l’appel, nous supposons que la précondition est vraie (puisque la fonction ne peut pas modifier la valeur reçue en paramètre), sinon la fonction n’aurait pas pu s’exécuter correctement. Par conséquent, nous supposons que INT_MIN < INT_MIN qui est trivialement faux. À partir de là, nous pouvons prouver tout ce que nous voulons, car ce « faux » devient une supposition pour tout appel qui viendrait ensuite. À partir de « faux », nous prouvons tout ce que nous voulons, car si nous avons la preuve de « faux » alors « faux » est vrai, de même que « vrai » est vrai. Donc tout est vrai.

En prenant le programme modifié, nous pouvons d’ailleurs regarder les obligations de preuve générées par WP pour l’appel fautif et l’appel prouvé par conséquent :

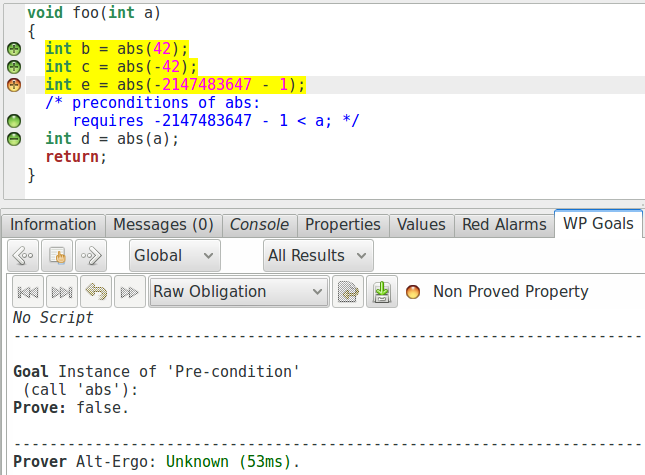
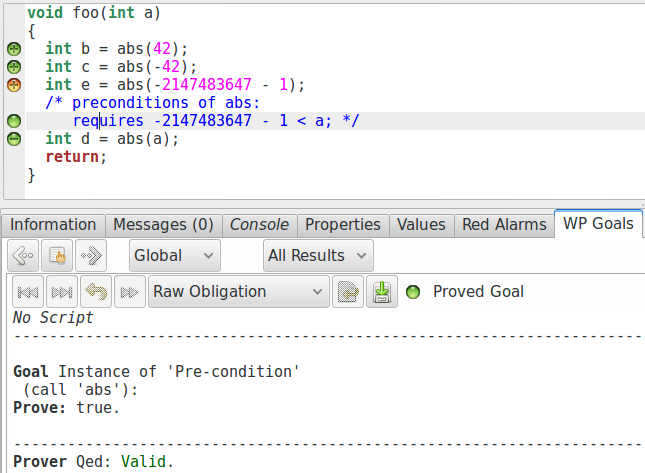
Nous pouvons remarquer que pour les appels de fonctions, l’interface graphique surligne le chemin d’exécution suivi avant l’appel dont nous cherchons à vérifier la précondition. Ensuite, si nous regardons l’appel abs(INT_MIN), nous remarquons qu’à force de simplifications, Qed a déduit que nous cherchons à prouver « False ». Conséquence logique, l’appel suivant abs(a) reçoit dans ses suppositions « False ». C’est pourquoi Qed est capable de déduire immédiatement « True ».

La deuxième partie de la question est alors : pourquoi lorsque nous mettons les appels dans l’autre sens (abs(a) puis abs(INT_MIN)), nous obtenons quand même une violation de la précondition sur le deuxième ? La réponse est simplement que pour abs(a) nous ajoutons dans nos suppositions la connaissance a < INT_MIN, et tandis que nous n’avons pas de preuve que c’est vrai, nous n’en avons pas non plus que c’est faux. Donc si nous obtenons nécessairement une preuve de « faux » avec un appel abs(INT_MIN), ce n’est pas le cas de l’appel abs(a) qui peut aussi ne pas échouer.

Exercices

Ces exercices ne sont pas absolument nécessaires pour lire les chapitres à venir dans ce tutoriel, nous conseillons quand même de les réaliser. Nous suggérons aussi fortement d’au moins lire le quatrième exercice qui introduit une notation qui peut parfois d’avérer utile.

Addition

Écrire la postcondition de la fonction d’addition suivante :

int add(int x, int y){
  return x+y ;
}

Lancer la commande :

frama-c-gui your-file.c -wp

Lorsque la preuve que la fonction respecte son contrat est établie, lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

qui devrait échouer. Adapter le contrat en ajoutant la bonne précondition.

Distance

Écrire la postcondition de la fonction distance suivante, en exprimant la valeur de b en fonction de aet\result` :

int distance(int a, int b){
  if(a < b) return b - a ;
  else return a - b ;
}

Lancer la commande :

frama-c-gui your-file.c -wp

Lorsque la preuve que la fonction respecte son contrat est établie, lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

qui devrait échouer. Adapter le contrat en ajoutant la bonne précondition.

Lettres de l’alphabet

Écrire la postcondition de la fonction suivante, qui retourne vrai si le caractère reçu en entrée est une lettre de l’alphabet. Utiliser la relation d’équivalence <==>.

int alphabet_letter(char c){
  if( ('a' <= c && c <= 'z') || ('A' <= c && c <= 'Z') ) return 1 ;
  else return 0 ;
}

int main(){
  int r ;

  r = alphabet_letter('x') ;
  //@ assert r ;
  r = alphabet_letter('H') ;
  //@ assert r ;
  r = alphabet_letter(' ') ;
  //@ assert !r ;
}

Lancer la commande :

frama-c-gui your-file.c -wp

Toutes les obligations de preuve devraient être prouvées, y compris les assertions dans la fonction main.

Jours du mois

Écrire la postcondition de la fonction suivante qui retourne le nombre de jours en fonction du mois reçu en entrée (NB: nous considérons que le mois reçu est entre 1 et 12), pour février, nous considérons uniquement le cas où il a 28 jours, nous verrons plus tard comment régler ce problème :

int day_of(int month){
  int days[] = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 } ;
  return days[month-1] ;
}

Lancer la commande :

frama-c-gui your-file.c -wp

Lorsque la preuve que la fonction respecte son contrat est établie, lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Si cela échoue, adapter le contrat en ajoutant la bonne précondition.

Le lecteur aura peut-être constaté qu’écrire la postcondition est un peu laborieux. Il est possible de simplifier cela. ACSL fournit la notion d’ensemble mathématique et l’opérateur \in qui peut être utilisé pour vérifier si une valeur est dans un ensemble ou non.

Par exemple :

//@ assert 13 \in { 1, 2, 3, 4, 5 } ; // FAUX
//@ assert 3  \in { 1, 2, 3, 4, 5 } ; // VRAI

Modifier la postcondition en utilisant cette notation.

Le dernier angle d’un triangle

Cette fonction reçoit deux valeurs d’angle en entrée et retourne la valeur du dernier angle composant le triangle correspondant en se reposant sur la propriété que la somme des angles d’un triangle vaut 180 degrés. Écrire la postcondition qui exprime que la somme des trois angle vaut 180.

int last_angle(int first, int second){
  return 180 - first - second ;
}

Lancer la commande :

frama-c-gui your-file.c -wp

Lorsque la preuve que la fonction respecte son contrat est établie, lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Si cela échoue, adapter le contrat en ajoutant la bonne précondition. Notons que la valeur de chaque angle ne peut pas être supérieure à 180 et que cela inclut l’angle résultant.

Bien traduire ce qui est attendu

C’est certainement notre tâche la plus difficile. En soi, la programmation est déjà un effort consistant à écrire des algorithmes qui répondent à notre besoin. La spécification nous demande également de faire ce travail, la différence est que nous ne nous occupons plus de préciser la manière de répondre au besoin mais le besoin lui-même. Pour prouver que la réalisation implémente bien ce que nous attendons, il faut donc être capable de décrire précisément le besoin.

Changeons d’exemple et spécifions la fonction suivante :

int max(int a, int b){
  return (a > b) ? a : b;
}

Le lecteur pourra écrire et prouver sa spécification. Pour la suite, nous travaillerons avec celle-ci :

/*@
  ensures \result >= a && \result >= b;
*/
int max(int a, int b){
  return (a > b) ? a : b;
}

Si nous donnons ce code à WP, il accepte sans problème de prouver la fonction. Pour autant cette spécification est-elle suffisante ? Nous pouvons par exemple essayer de voir si ce code est validé :

void foo(){
  int a = 42;
  int b = 37;
  int c = max(a,b);

  //@assert c == 42;
}

La réponse est non. En fait, nous pouvons aller plus loin en modifiant le corps de la fonction max et remarquer que le code suivant est également valide quant à la spécification :

#include <limits.h>

/*@
  ensures \result >= a && \result >= b;
*/
int max(int a, int b){
  return INT_MAX;
}

Même si elle est correcte, notre spécification est trop permissive. Il faut que nous soyons plus précis. Nous attendons du résultat non seulement qu’il soit supérieur ou égal à nos deux paramètres mais également qu’il soit exactement l’un des deux :

/*@
  ensures \result >= a && \result >= b;
  ensures \result == a || \result == b;
*/
int max(int a, int b){
  return (a > b) ? a : b;
}

Nous pouvons également prouver que cette spécification est vérifiée par notre fonction. Mais nous pouvons maintenant prouver en plus l’assertion présente dans notre fonction foo, et nous ne pouvons plus prouver que l’implémentation qui retourne INT_MAX vérifie la spécification.

Préconditions incohérentes

Bien spécifier son programme est d’une importance cruciale. Typiquement, préciser une précondition fausse peut nous donner la possibilité de prouver FAUX :

/*@
  requires a < 0 && a > 0;
  ensures \false;
*/
void foo(int a){

}

Si nous demandons à WP de prouver cette fonction. Il l’acceptera sans rechigner, car la propriété que nous lui donnons comme précondition est nécessairement fausse. Par contre, nous aurons bien du mal à lui donner une valeur en entrée qui respecte la précondition.

Pour cette catégorie particulière d’incohérences, une fonctionnalité utile de WP est l’option « smoke tests » du greffon. Ces tests préliminaires, effectués sur notre spécification sont utilisés pour détecter que des préconditions ne peuvent pas être satisfaites. Par exemple, ici, nous pouvons lancer cette ligne de commande :

frama-c-gui -wp -wp-smoke-tests file.c

et nous obtenons le résultat suivant dans l’interface graphique :

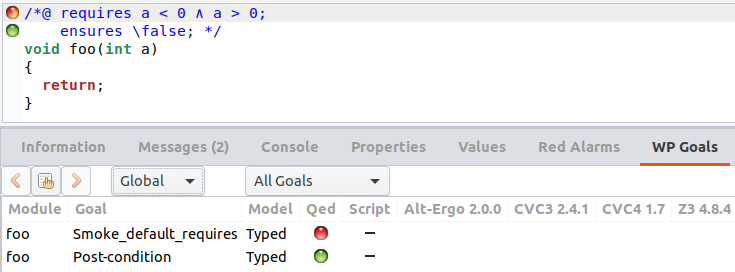
Nous pouvons voir une pastille orange et rouge à côté de la précondition de la fonction, qui signifie que s’il existe un appel atteignable à la fonction dans le programme, la précondition sera nécessairement violée lors de cet appel ; et une pastille rouge dans la liste des obligations de preuve, indiquant qu’un prouveur a réussi à montrer que la précondition est incohérente.

Notons que lorsque ces tests préliminaires réussissent, par exemple si nous corrigeons la précondition de cette façon :

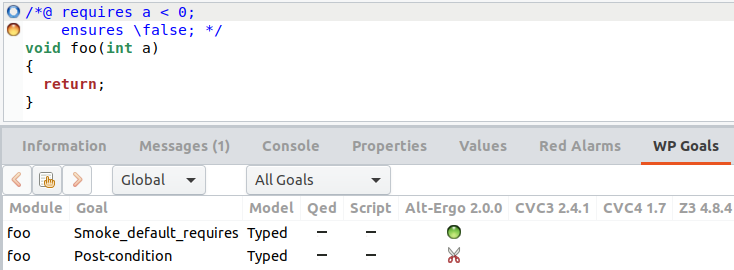
cela ne signifie pas que la précondition est nécessairement cohérente, juste qu’aucun prouveur n’a été capable de montrer qu’elle est incohérente.

Certaines notions que nous verrons plus loin dans le tutoriel apporterons un risque encore plus grand de créer ce genre d’incohérence. Il faut donc toujours avoir une attention particulière pour ce que nous spécifions.

Pointeurs

S’il y a une notion à laquelle nous sommes confrontés en permanence en langage C, c’est bien la notion de pointeur. C’est une notion complexe et l’une des principales cause de bugs critiques dans les programmes, ils ont donc droit à un traitement de faveur dans ACSL. Pour avoir une spécification correcte des programmes utilisant des pointeurs, il est impératif de détailler la configuration de la mémoire que l’on considère.

Prenons par exemple une fonction swap pour les entiers :

/*@
  ensures *a == \old(*b) && *b == \old(*a);
*/
void swap(int* a, int* b){
  int tmp = *a;
  *a = *b;
  *b = tmp;
}

Historique des valeurs

Ici, nous introduisons une première fonction logique fournie de base par ACSL : \old, qui permet de parler de l’ancienne valeur d’un élément. Ce que nous dit donc la spécification c’est « la fonction doit assurer que a soit égal à l’ancienne valeur (au sens : la valeur avant l’appel) de b et inversement ».

La fonction \old ne peut être utilisée que dans la postcondition d’une fonction. Si nous avons besoin de ce type d’information ailleurs, nous utilisons \at qui nous permet d’exprimer des propriétés à propos de la valeur d’une variable à un point donné. Elle reçoit deux paramètres. Le premier est la variable (ou position mémoire) dont nous voulons obtenir la valeur et le second la position (sous la forme d’un label C) à laquelle nous voulons contrôler la valeur en question.

Par exemple, nous pourrions écrire :

  int a = 42;
 Label_a:
  a = 45;

  //@assert a == 45 && \at(a, Label_a) == 42;

En plus des labels que nous pouvons nous-mêmes créer, il existe 6 labels qu’ACSL nous propose par défaut, mais tous ne sont pas supportés par WP :

• Pre/Old : valeur avant l’appel de la fonction,
• Post : valeur après l’appel de la fonction,
• LoopEntry : valeur en début de boucle,
• LoopCurrent : valeur en début du pas actuel de la boucle,
• Here : valeur au point d’appel.

À la différence de \old, qui ne peut être utilisée que dans les postconditions de contrats de fonction, \at peut être utilisée partout. En revanche, tous les points de programme ne sont pas accessibles selon le type d’annotation que nous sommes en train d’écrire. Old et Post ne sont disponibles que dans les postconditions d’un contrat, Pre et Here sont disponibles partout. LoopEntry et LoopCurrent ne sont disponibles que dans le contexte de boucles (dont nous parlerons plus loin dans le tutoriel).

Notons qu’il est important de s’assurer que l’on utilise \old et \at pour des valeurs qui ont du sens. C’est pourquoi par exemple dans un contrat, toutes les valeurs reçues en entrée sont placées dans un appel à \old par Frama-C lorsqu’elles sont utilisées dans les postconditions, la nouvelle valeur d’une variable fournie en entrée d’une fonction n’a aucun sens pour l’appelant puisque cette valeur est inaccessible par lui : elles sont locales à la fonction appelée. Par exemple, si nous regardons le contrat de la fonction swap dans Frama-C, nous pouvons voir que dans la postcondition, chaque pointeur se trouve dans un appel à \old :

Pour la fonction built-in \at, nous devons plus explicitement faire attention à cela. En particulier, le label transmis en entrée doit avoir un sens par rapport à la portée de la variable que l’on lui transmet. Par exemple, dans le programme suivant, Frama-C détecte que nous demandons la valeur de la variable x à un point du programme où elle n’existe pas:

void example_1(void){
 L: ;
  int x = 1 ;
  //@ assert \at(x, L) == 1 ;
}

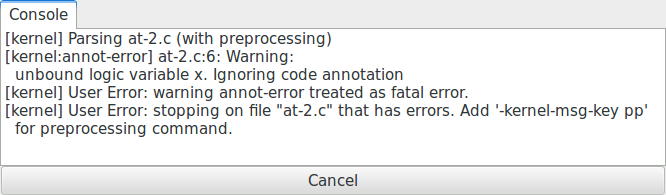
Cependant, dans certains cas, tout ce que nous pouvons obtenir est un échec de la preuve, parce que déterminer si la valeur existe ou non à un label particulier ne peut être fait par une analyse purement syntaxique. Par exemple, si la variable est déclarée mais pas définie, ou si nous demandons la valeur d’une zone mémoire pointée :

void example_2(void){
  int x ;
 L:
  x = 1 ;
  //@ assert \at(x, L) == 1 ;
}

void example_3(void){
 L: ;
  int x = 1 ;
  int *ptr = &x ;
  //@ assert \at(*\at(ptr, Here), L) == 1 ;
}

Ici, il est facile de remarquer le problème. Cependant, le label que nous transmettons à la fonction \at est propagé également aux sous-expressions. Dans certains cas, des termes qui paraissent tout à fait innocents peuvent en réalité nous donner des comportements surprenants si nous ne gardons pas cette idée en tête. Par exemple, dans le programme suivant :

/*@ requires x + 2 != p ; */
void example_4(int* x, int* p){
  *p = 2 ;
  //@ assert x[2]  == \at(x[2], Pre) ;
  //@ assert x[*p] == \at(x[*p], Pre) ;
}

La première assertion est prouvée, et tandis que la seconde assertion a l’air d’exprimer la même propriété, elle ne peut pas être prouvée. La raison est simplement qu’elle n’exprime pas la même propriété. L’expression \at(x[*p], Pre) doit être lue comme \at(x[\at(*p)], Pre) parce que le label est propagé à la sous-expression *p, pour laquelle nous ne connaissons pas la valeur au label Pre (qui n’est pas spécifié).

Pour le moment, nous n’utiliserons pas \at, mais elle peut rapidement se montrer indispensable pour écrire des spécifications précises.

Validité de pointeurs

Si nous essayons de prouver le fonctionnement de swap (en activant la vérification des RTE), notre postcondition est bien vérifiée mais WP nous indique qu’il y a un certain nombre de possibilités de runtime-error. Ce qui est normal, car nous n’avons pas précisé à WP que les pointeurs que nous recevons en entrée de fonction sont valides.

Pour ajouter cette précision, nous allons utiliser le prédicat \valid qui reçoit un pointeur en entrée :

/*@
  requires \valid(a) && \valid(b);
  ensures  *a == \old(*b) && *b == \old(*a);
*/
void swap(int* a, int* b){
  int tmp = *a;
  *a = *b;
  *b = tmp;
}

À partir de là, les déréférencements qui sont effectués par la suite sont acceptés car la fonction demande à ce que les pointeurs d’entrée soient valides.

Comme nous le verrons plus tard, \valid peut recevoir plus qu’un pointeur en entrée. Par exemple, il est possible de lui transmettre une expression de cette forme : \valid(p + (s .. e)) qui voudra dire « pour tout i entre s et e (inclus), p+i est un pointeur valide », ce sera important notamment pour la gestion des tableaux dans les spécifications.

Si nous nous intéressons aux assertions ajoutées par WP dans la fonction swap avec la validation des RTEs, nous pouvons constater qu’il existe une variante de \valid sous le nom \valid_read. Contrairement au premier, celui-ci assure qu’il est uniquement nécessaire que le pointeur puisse être déréférencé en lecture et pas forcément en écriture, pour pouvoir réaliser l’opération de lecture. Cette subtilité est due au fait qu’en C, le downcast de pointeur vers un élément const est très facile à faire mais n’est pas forcément légal.

Typiquement, dans le code suivant :

/*@ requires \valid(p); */
int unref(int* p){
  return *p;
}

int const value = 42;

int main(){
  int i = unref(&value);
}

Le déréférencement de p est valide, pourtant la pré-condition de unref ne sera pas validée par WP, car le déréférencement de l’adresse de value n’est légal qu’en lecture. Un accès en écriture sera un comportement indéterminé. Dans un tel cas, nous pouvons préciser que dans unref, le pointeur p doit être nécessairement \valid_read et pas \valid.

Effets de bord

Notre fonction swap est bien prouvable au regard de sa spécification et de ses potentielles erreurs à l’exécution, mais est-elle pour autant suffisamment spécifiée ? Pour voir cela, nous pouvons modifier légèrement le code de cette façon (nous utilisons assert pour analyser des propriétés ponctuelles) :

int h = 42; //nous ajoutons une variable globale

/*@
  requires \valid(a) && \valid(b);
  ensures  *a == \old(*b) && *b == \old(*a);
*/
void swap(int* a, int* b){
  int tmp = *a;
  *a = *b;
  *b = tmp;
}

int main(){
  int a = 37;
  int b = 91;

  //@ assert h == 42;
  swap(&a, &b);
  //@ assert h == 42;
}

Le résultat n’est pas vraiment celui escompté :

En effet, nous n’avons pas spécifié les effets de bords autorisés pour notre fonction. Pour cela, nous utilisons la clause assigns qui fait partie des postconditions de la fonction. Elle nous permet de spécifier quels éléments non locaux (on vérifie bien des effets de bord), sont susceptibles d’être modifiés par la fonction.

Par défaut, WP considère qu’une fonction a le droit de modifier n’importe quel élément en mémoire. Nous devons donc préciser ce qu’une fonction est en droit de modifier. Par exemple pour notre fonction swap, nous pouvons spécifier que seules les valeurs pointées par les pointeurs reçus peuvent être modifiées :

/*@
  requires \valid(a) && \valid(b);
 
  assigns *a, *b;

  ensures  *a == \old(*b) && *b == \old(*a);
*/
void swap(int* a, int* b){
  int tmp = *a;
  *a = *b;
  *b = tmp;
}

Si nous rejouons la preuve avec cette spécification, la fonction et les assertions que nous avions demandées dans le main seront validées par WP.

Finalement, il peut arriver que nous voulions spécifier qu’une fonction ne provoque pas d’effets de bords. Ce cas est précisé en donnant \nothing à assigns :

/*@ 
  requires \valid_read(a);
  requires *a <= INT_MAX - 5 ;
  assigns \nothing ;
  ensures \result == *a + 5 ; 
*/
int plus_5(int* a){
  return *a + 5 ;
}

Le lecteur pourra maintenant reprendre les exemples précédents pour y intégrer la bonne clause assigns.

Séparation des zones de la mémoire

Les pointeurs apportent le risque d'aliasing (plusieurs pointeurs ayant accès à la même zone de mémoire). Si dans certaines fonctions, cela ne pose pas de problème (par exemple si nous passons deux pointeurs égaux à notre fonction swap, la spécification est toujours vérifiée par le code source), dans d’autre cas, ce n’est pas si simple :

#include <limits.h>

/*@
  requires \valid(a) && \valid_read(b);
  assigns  *a;
  ensures  *a == \old(*a)+ *b;
  ensures  *b == \old(*b);
*/
void incr_a_by_b(int* a, int const* b){
  *a += *b;
}

Si nous demandons à WP de prouver cette fonction, nous obtenons le résultat suivant :

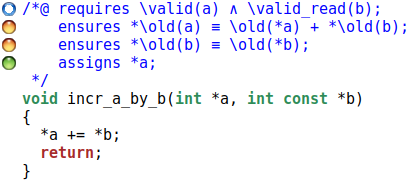
La raison est simplement que rien ne garantit que le pointeur a est bien différent du pointeur b. Or, si les pointeurs sont égaux,

• la propriété *a == \old(*a) + *b signifie en fait *a == \old(*a) + *a, ce qui ne peut être vrai que si l’ancienne valeur pointée par a était 0, ce qu’on ne sait pas,
• la propriété *b == \old(*b) n’est pas validée car potentiellement, nous la modifions.

Pour assurer que les pointeurs sont bien sur des zones séparées de mémoire, ACSL nous offre le prédicat \separated(p1, ..., pn) qui reçoit en entrée un certain nombre de pointeurs et qui nous assurera qu’ils sont deux à deux disjoints. Ici, nous spécifierions :

#include <limits.h>

/*@
  requires \valid(a) && \valid_read(b);
  requires \separated(a, b);
  assigns  *a;
  ensures  *a == \old(*a)+ *b;
  ensures  *b == \old(*b);
*/
void incr_a_by_b(int* a, int const* b){
  *a += *b;
}

Et cette fois, la preuve est effectuée :

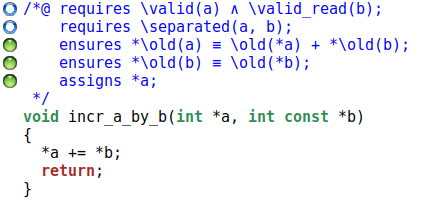
Nous pouvons noter que nous ne nous intéressons pas ici à la preuve de l’absence d’erreur à l’exécution, car ce n’est pas l’objet de cette section. Cependant, si cette fonction faisait partie d’un programme complet à vérifier, il faudrait définir le contexte dans lequel on souhaite l’utiliser et définir les pré-conditions qui nous garantissent l’absence de débordement en conséquence.

Écrire le bon contrat

Trouver les bonnes pré-conditions à une fonction est parfois difficile. Il est intéressant de noter qu’une bonne manière de vérifier qu’une spécification est suffisamment précise est d’écrire des tests pour voir si le contrat nous permet, depuis un code appelant, de déduire des propriétés intéressantes. En fait, c’est exactement ce que nous avons fait pour nos exemples \CodeInline{max} et \CodeInline{swap}. Nous avons écrit une première version de notre spécification et du code appelant qui nous a servi à déterminer si nous pouvions prouver des propriétés que nous estimions devoir être capables de prouver à l’aide du contrat.

Le plus important est avant tout de déterminer le contrat sans prendre en compte le contenu de la fonction (au moins dans un premier temps). En effet, nous essayons de prouver une fonction, mais elle pourrait contenir un bug, donc si nous suivons de trop près le code de la fonction, nous risquons d’introduire dans la spécification le même bug présent dans le code, par exemple en prenant en compte une condition erronée. C’est pour cela que l’on souhaitera généralement que la personne qui développe le programme et la personne qui le spécifie formellement soient différentes (même si elles ont pu préalablement s’accorder sur une spécification textuelle par exemple).

Une fois que le contrat est posé, alors seulement, nous nous intéressons aux spécifications dues au fait que nous sommes soumis aux contraintes de notre langage et notre matériel. Cela concerne principalement nos préconditions. Par exemple, la fonction valeur absolue n’a, au fond, pas vraiment de pré-condition à respecter, c’est la machine cible qui détermine qu’une condition supplémentaire doit être respectée en raison du complément à deux. Comme nous le verrons dans le chapitre \ref{l1:proof-methodologies}, vérifier l’absence de runtime errors peut aussi impacter nos postconditions, pour l’instant laissons cela de côté.

Exercices

Division et reste

Spécifier la postcondition de la fonction suivante, qui calcule le résultat de la division de a par b et le reste de cette division et écrit ces deux valeurs à deux positions mémoire p et q :

void div_rem(unsigned x, unsigned y, unsigned* q, unsigned* r){
  *q = x / y ;
  *r = x % y ;
}

Lancer la commande :

frama-c-gui your-file.c -wp 

Une fois que la fonction est prouvée, lancer :

frama-c-gui your-file.c -wp -wp-rte

Si cela échoue, compléter le contrat en ajoutant la bonne précondition.

Remettre à zéro selon une condition

Donner un contrat à la fonction suivante qui remet à zéro la valeur pointée par le premier paramètre si et seulement si celle pointée par le second est vraie. Ne pas oublier d’exprimer que la valeur pointée par le second paramètre doit rester la même :

void reset_1st_if_2nd_is_true(int* a, int const* b){
  if(*b) *a = 0 ;
}

int main(){
  int a = 5 ;
  int x = 0 ;

  reset_1st_if_2nd_is_true(&a, &x);
  //@ assert a == 5 ;
  //@ assert x == 0 ;
  
  int const b = 1 ;

  reset_1st_if_2nd_is_true(&a, &b);
  //@ assert a == 0 ;
  //@ assert b == 1 ;
}

Lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Addition de valeurs pointées

La fonction suivante reçoit deux pointeurs en entrée et retourne la somme des valeurs pointées. Écrire le contrat de cette fonction :

int add(int *p, int *q){
  return *p + *q ;
}

int main(){
  int a = 24 ;
  int b = 42 ;

  int x ;

  x = add(&a, &b) ;
  //@ assert x == a + b ;
  //@ assert x == 66 ;

  x = add(&a, &a) ;
  //@ assert x == a + a ;
  //@ assert x == 48 ;
}

Lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Une fois que la fonction et son code appelant sont prouvées, modifier la signature de la fonction comme suit :

void add(int* a, int* b, int* r);

Le résultat doit maintenant être stocké à la position mémoire r. Modifier l’appel dans la fonction main et le code de la fonction de façon à implémenter ce comportement. Modifier le contrat de la fonction add et recommencer la preuve.

Maximum de valeurs pointées

Le code suivant calcule le maximum des valeurs pointées par a et b. Écrire le contrat de cette fonction :

int max_ptr(int* a, int* b){
  return (*a < *b) ? *b : *a ;
}

extern int h ;

int main(){
  h = 42 ;

  int a = 24 ;
  int b = 42 ;

  int x = max_ptr(&a, &b) ;

  //@ assert x == 42 ;
  //@ assert h == 42 ;
}

Lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Une fois que la fonction est prouvée, modifier la signature de la fonction comme suit :

void max_ptr(int* a, int* b);

La fonction doit maintenant s’assurer qu’après l’exécution, *a contient le maximum des valeurs pointées et *b contient l’autre valeur. Modifier le code de façon à assurer cela ainsi que le contrat. Notons que la variable x n’est plus nécessaire dans la fonction main et que nous pouvons changer l’assertion en ligne 15 pour mettre en lumière le nouveau comportement de la fonction.

Ordonner trois valeurs

La fonction suivante doit ordonner trois valeurs reçues en entrée dans l’ordre croissant. Écrire le code correspondant et la spécification de la fonction :

void order_3(int* a, int* b, int* c){
  // CODE
}

Et lancer la commande :

frama-c-gui your-file.c -wp -wp-rte

Il faut bien garder en tête qu’ordonner des valeurs ne consiste pas seulement à s’assurer qu’elles sont dans l’ordre croissant et que chaque valeur doit être l’une de celles d’origine. Toutes les valeurs d’origine doivent être présente et en même quantité. Pour exprimer cette idée, nous pouvons nous reposer à nouveau sur les ensembles. La propriété suivante est vraie par exemple :

//@ assert { 1, 2, 3 } == { 2, 3, 1 };

Nous pouvons l’utiliser pour exprimer que l’ensemble des valeurs d’entrée et de sortie est le même. Cependant, ce n’est pas la seule chose à prendre en compte car un ensemble ne contient qu’une occurrence de chaque valeur. Donc, si *a == *b == 1, alors { *a, *b } == { 1 }. Par conséquent nous devons considérer trois autres cas particuliers:

• toutes les valeurs d’origine sont les mêmes ;
• deux valeurs d’origine sont les mêmes, la dernière est plus grande ;
• deux valeurs d’origine sont les mêmes, la dernière est plus petite.

Qui nous permet d’ajouter la bonne contrainte aux valeurs de sortie.

Pour la réalisation de la spécification, le programme de test suivant peut nous aider :

void test(){
  int a1 = 5, b1 = 3, c1 = 4 ;
  order_3(&a1, &b1, &c1) ;
  //@ assert a1 == 3 && b1 == 4 && c1 == 5 ;

  int a2 = 2, b2 = 2, c2 = 2 ;
  order_3(&a2, &b2, &c2) ;
  //@ assert a2 == 2 && b2 == 2 && c2 == 2 ;

  int a3 = 4, b3 = 3, c3 = 4 ;
  order_3(&a3, &b3, &c3) ;
  //@ assert a3 == 3 && b3 == 4 && c3 == 4 ;

  int a4 = 4, b4 = 5, c4 = 4 ;
  order_3(&a4, &b4, &c4) ;
  //@ assert a4 == 4 && b4 == 4 && c4 == 5 ;
}

Si la spécification est suffisamment précise, chaque assertion devrait être prouvée. Cependant, cela ne signifie pas que tous les cas ont été considérés, il ne faut pas hésiter à ajouter d’autres tests.

Il peut arriver qu’une fonction ait divers comportements potentiellement très différents en fonction de l’entrée. Un cas typique est la réception d’un pointeur vers une ressource optionnelle : si le pointeur est NULL, nous aurons un certain comportement et un comportement complètement différent s’il ne l’est pas.

Nous avons déjà vu une fonction qui avait des comportements différents, la fonction abs. Nous la reprendrons comme exemple. Les deux comportements que nous pouvons isoler sont le cas où la valeur est positive et le cas où la valeur est négative.

Les comportements nous servent à spécifier les différents cas pour les postconditions. Nous les introduisons avec le mot-clé behavior. Chaque comportement a un nom. Pour un comportement donné, nous trouvons différentes hypothèses à propos de l’entrée de la fonction, elles sont introduites à l’aide du mot-clé assumes (notons que, puisqu’elles caractérisent les entrées, le mot-clé \old ne peut pas être utilisé ici). Cependant, chaque propriété exprimée par ces clauses n’a pas besoin d’être vérifiée avant à l’appel, elle peut être vérifiée et dans ce cas, les postconditions associées à ce comportement s’appliquent. Ces postconditions sont à nouveau introduites à l’aide du mot clé ensures. Finalement, nous pouvons également demander à WP de vérifier le fait que les comportements sont disjoints (pour garantir le déterminisme) et complets (pour garantir que nous couvrons toutes les entrées possibles).

Les comportements sont disjoints si pour toute entrée de la fonction, elle ne correspond aux hypothèses (assumes) que d’un seul comportement. Les comportements sont complets si les hypothèses recouvrent bien tout le domaine des entrées.

Par exemple pour abs :

/*@
  requires val > INT_MIN;
  assigns  \nothing;

  behavior pos:
    assumes 0 <= val;
    ensures \result == val;
  
  behavior neg:
    assumes val < 0;
    ensures \result == -val;
 
  complete behaviors;
  disjoint behaviors;
*/
int abs(int val){
  if(val < 0) return -val;
  return val;
}

Notons qu’introduire des comportements ne nous interdit pas de spécifier une postcondition globale. Par exemple ici, nous avons spécifié que quel que soit le comportement, la fonction doit retourner une valeur positive.

Pour comprendre ce que font précisément complete et disjoint, il est utile d’expérimenter deux possibilités :

• remplacer l’hypothèse de « pos » par val > 0 auquel cas les comportements seront disjoints mais incomplets (il nous manquera le cas val == 0) ;
• remplacer l’hypothèse de « neg » par val <= 0 auquel cas les comportements seront complets mais non disjoints (le cas val == 0) sera présent dans les deux comportements.

Les comportements sont très utiles pour simplifier l’écriture de spécifications quand les fonctions ont des effets très différents en fonction de leurs entrées. Sans eux, les spécifications passent systématiquement par des implications traduisant la même idée mais dont l’écriture et la lecture sont plus difficiles (nous sommes susceptibles d’introduire des erreurs).

D’autre part, la traduction de la complétude et de la disjonction devraient être écrites manuellement, ce qui serait fastidieux et une nouvelle fois source d’erreurs.

Exercices

Exercices précédents

Dans les sections précédentes, reprendre les exemples :

• à propos du calcul de la distance entre deux entiers ;
• « Remettre à zéro selon une condition » ;
• « Jours du mois » ;
• « Maximum des valeurs pointées ».

En considérant que les contrats étaient :

#include <limits.h>

/*@
  requires a < b  ==> b - a <= INT_MAX ;
  requires b <= a ==> a - b <= INT_MAX ;

  ensures a < b  ==> a + \result == b ;
  ensures b <= a ==> a - \result == b ;
*/
int distance(int a, int b){
  if(a < b) return b - a ;
  else return a - b ;
}

/*@
  requires \valid(a) && \valid_read(b) ;
  requires \separated(a, b) ;

  assigns *a ;

  ensures \old(*b) ==> *a == 0 ;
  ensures ! \old(*b) ==> *a == \old(*a) ;
  ensures *b == \old(*b);
*/
void reset_1st_if_2nd_is_true(int* a, int const* b){
  if(*b) *a = 0 ;
}

/*@
  requires 1 <= m <= 12 ;
  ensures m \in { 2 } ==> \result == 28 ;
  ensures m \in { 1, 3, 5, 7, 8, 10, 12 } ==> \result == 31 ;
  ensures m \in { 4, 6, 9, 11 } ==> \result == 30 ;
*/
int day_of(int m){
  int days[] = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 } ;
  return days[m-1] ;
}

/*@
  requires \valid(a) && \valid(b);
  assigns  *a, *b ;
  ensures  \old(*a) < \old(*b)  ==> *a == \old(*b) && *b == \old(*a) ;
  ensures  \old(*a) >= \old(*b) ==> *a == \old(*a) && *b == \old(*b) ;
*/
void max_ptr(int* a, int* b){
  if(*a < *b){
    int tmp = *b ;
    *b = *a ;
    *a = tmp ;
  }
}

Les réécrire en utilisant des comportements.

Deux autres exercices simples

Produire le code et la spécification des deux fonctions suivantes puis les prouver. La spécification devrait faire usage des comportements.

Tout d’abord une fonction qui retourne si un caractère est une voyelle ou une consonne, supposer (et exprimer) que la fonction reçoit une lettre minuscule.

enum Kind { VOWEL, CONSONANT };

enum Kind kind_of_letter(char c){
  // ...
}

Puis une fonction qui renvoie à quel quadrant d’un repère appartient une coordonnée. Lorsque la coordonnée se trouve sur un axe, choisir arbitrairement l’un des quadrant qu’elle touche.

int quadrant(int x, int y){
  // ...
}

Triangle

Compléter les fonctions suivantes qui reçoivent la longueur des différents côté et retournent respectivement :

• si le triangle est scalène, isocèle, ou équilatéral ;
• si le triangle est rectangle, acutangle ou obtusangle.

#include <limits.h>

enum Sides { SCALENE, ISOSCELE, EQUILATERAL };
enum Angles { RIGHT, ACUTE, OBTUSE };

enum Sides sides_kind(int a, int b, int c){
  // ...
}

enum Angles angles_kind(int a, int b, int c){
  //
}

En supposant (et exprimant) que :

• les valeurs reçues forment bien un triangle,
• a est l’hypoténuse du triangle,

spécifier et prouver que les fonctions font la tâche prévue.

Maximum des valeurs pointées

Reprendre l’exemple « Maximum des valeurs pointées » de la section précédente et plus précisément la version qui retourne la plus grande valeur. En considérant que le contrat était :

/*@
  requires \valid_read(a) && \valid_read(b);
  assigns  \nothing ;
  ensures  *a <  *b ==> \result == *b ;
  ensures  *a >= *b ==> \result == *a ;
  ensures  \result == *a || \result == *b ;
*/
int max_ptr(int* a, int* b){
  return (*a < *b) ? *b : *a ;
}

1. Le réécrire en utilisant des comportements
2. Modifier le contrat de 1. de sorte que les comportements ne soient pas disjoints. Excepté cette propriété, tout le reste devrait être correctement prouvé
3. Modifier le contrat de 1. de sorte que les comportements ne soient pas complets, puis ajouter un nouveau comportement pour le rendre de nouveau complet
4. Modifier la fonction de 1. de façon à accepter la valeur NULL pour les pointeurs d’entrées, si les deux pointeurs sont nuls, retourner INT_MIN, si l’un seulement est nul, retourner l’autre valeur, sinon retourner le maximum des deux valeurs. Modifier le contrat de façon à prendre en compte tout cela par de nouveaux comportements. Prendre soin d’assurer que les comportements sont complets et disjoints.

Ordonner trois valeurs

Reprendre l’exemple « Ordonner trois valeurs » de la section précédente, en considérant que le contrat était :

/*@
  requires \valid(a) && \valid(b) && \valid(c) ;
  requires \separated(a, b, c);
  assigns *a, *b, *c ;
  ensures *a <= *b <= *c ;
  ensures { *a, *b, *c } == \old({ *a, *b, *c }) ;
  
  ensures \old(*a == *b == *c) ==> *a == *b == *c ;
  ensures \old(*a == *b < *c || *a == *c < *b || *b == *c < *a) ==> *a == *b ;
  ensures \old(*a == *b > *c || *a == *c > *b || *b == *c > *a) ==> *b == *c ;
*/
void order_3(int* a, int* b, int* c){
  if(*a > *b){ int tmp = *b ; *b = *a ; *a = tmp ; }
  if(*a > *c){ int tmp = *c ; *c = *a ; *a = tmp ; }
  if(*b > *c){ int tmp = *b ; *b = *c ; *c = tmp ; }
}

Le réécrire en utilisant des comportements. Notons que le contrat devrait être composé d’un comportement général et de trois comportements spécifiques. Est-ce que ces comportements sont complets ? Sont-ils disjoints ?

Pour terminer cette partie nous allons parler de la composition des appels de fonctions et commencer à entrer dans les détails de fonctionnement de WP. Nous en profiterons pour regarder comment se traduit le découpage de nos programmes en fichiers lorsque nous voulons les spécifier et les prouver avec WP.

Notre but sera de prouver la fonction max_abs qui renvoie les maximums entre les valeurs absolues de deux valeurs :

int max_abs(int a, int b){
  int abs_a = abs(a);
  int abs_b = abs(b);

  return max(abs_a, abs_b);
}

Commençons par (sur-)découper les déclarations et définitions des différentes fonctions dont nous avons besoin (et que nous avons déjà prouvé) en couples headers/source, à savoir abs et max. Cela donne pour abs :

Fichier abs.h :

#ifndef _ABS
#define _ABS

#include <limits.h>

/*@
  requires val > INT_MIN;
  assigns  \nothing;

  behavior pos:
    assumes 0 <= val;
    ensures \result == val;
  
  behavior neg:
    assumes val < 0;
    ensures \result == -val;
 
  complete behaviors;
  disjoint behaviors;
*/
int abs(int val);

#endif

Fichier abs.c

#include "abs.h"

int abs(int val){
  if(val < 0) return -val;
  return val;
}

Nous découpons en mettant le contrat de la fonction dans le header. Le but est de pouvoir importer la spécification en même temps que la déclaration de celle-ci lorsque nous aurons besoin de la fonction dans un autre fichier. En effet, WP en aura besoin pour montrer que les appels à cette fonction sont valides. D’abord pour prouver que la précondition est respectée (et donc que l’appel est légal) et ensuite pour savoir ce qu’il peut apprendre en retour (à savoir la postcondition) afin de pouvoir l’utiliser pour prouver la fonction appelante.

Nous pouvons créer un fichier sous le même formatage pour la fonction max. Dans les deux cas, nous pouvons ré-ouvrir le fichier source (pas besoin de spécifier les fichiers headers dans la ligne de commande) avec Frama-C et remarquer que la spécification est bien associée à la fonction et que nous pouvons la prouver.

Maintenant, nous pouvons préparer le terrain pour la fonction max_abs dans notre header :

#ifndef _MAX_ABS
#define _MAX_ABS

int max_abs(int a, int b);

#endif

et dans le source :

#include "max_abs.h"
#include "max.h"
#include "abs.h"

int max_abs(int a, int b){
  int abs_a = abs(a);
  int abs_b = abs(b);

  return max(abs_a, abs_b);
}

Et ouvrir ce dernier fichier dans Frama-C. Si nous regardons le panneau latéral, nous pouvons voir que les fichiers header que nous avons inclus dans le fichier abs_max.c y apparaissent et que les contrats de fonction sont décorés avec des pastilles particulières (vertes et bleues) :

Ces pastilles nous disent qu’en l’absence d’implémentation, les propriétés sont supposées vraies. Et c’est une des forces de la preuve déductive de programmes par rapport à certaines autres méthodes formelles : les fonctions sont vérifiées en isolation les unes des autres.

En dehors de la fonction, sa spécification est considérée comme étant vérifiée : nous ne cherchons pas à reprouver que la fonction fait bien son travail à chaque appel, nous nous contenterons de vérifier que les préconditions sont réunies au moment de l’appel. Cela donne donc des preuves très modulaires et donc des spécifications plus facilement réutilisables. Évidemment, si notre preuve repose sur la spécification d’une autre fonction, cette fonction doit-elle même être vérifiable pour que la preuve soit formellement complète. Mais nous pouvons également vouloir simplement faire confiance à une bibliothèque externe sans la prouver.

Finalement, le lecteur pourra essayer de spécifier la fonction max_abs.

La spécification peut ressembler à ceci :

/*@
  requires a > INT_MIN;
  requires b > INT_MIN;
  assigns \nothing;
  ensures \result >= 0;
  ensures \result >= a && \result >= -a && \result >= b && \result >= -b;
  ensures \result == a || \result == -a || \result == b || \result == -b;
*/
int max_abs(int a, int b);

Exercices

Jours du mois

Spécifier la fonction année bissextile qui retourne vrai si l’année reçue en entrée est bissextile. Utiliser cette fonction pour compéter la fonction jours du mois de façon à retourner le nombre de jour du mois reçu en entrée, incluant le bon comportement lorsque le mois en question est février et que l’année est bissextile.

int leap(int y){
  return ((y % 4 == 0) && (y % 100 !=0)) || (y % 400==0) ;
}

int days_of(int m, int y){
  int days[] = { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 } ;
  int n = days[m-1] ;
  // code
}

Caractères alpha-numériques

Écrire et spécifier les différentes fonctions utilisées par is_alpha_num. Fournir un contrat pour chacune d’elles et fournir le contrat de is_alpha_num.

int is_alpha_num(char c){
  return
    is_lower_alpha(c) || 
    is_upper_alpha(c) ||
    is_digit(c) ;
}

Déclarer une énumération avec les valeurs LOWER, UPPER, DIGIT et OTHER, et une fonction character_kindqui retourne, en utilisant les différentes fonctions is_lower, is_upper et is_digit, la sorte de caractère reçue en entrée. Utiliser les comportements pour spécifier le contrat de cette fonction en s’assurant qu’ils sont complets et disjoints.

Ordonner trois valeurs

Reprendre la fonction max_ptr dans sa version qui « ordonne » les deux valeurs. Écrire une fonction min_ptr qui utilise la fonction précédente pour effectuer l’opération inverse. Utiliser ces fonctions pour compléter les quatre fonctions qui ordonnent trois valeurs. Pour chaque variante (ordre croissant et décroissant), l’écrire une première fois en utilisant uniquement max_ptr et une seconde en utilisant min_ptr. Écrire un contrat précis pour chacune de ces fonctions et les prouver.

void max_ptr(int* a, int* b){
  if(*a < *b){
    int tmp = *b ;
    *b = *a ;
    *a = tmp ;
  }
}

void min_ptr(int* a, int* b){
  // use max_ptr
}

void order_3_inc_max(int* a, int* b, int* c){
  //in increasing order using max_ptr
}

void order_3_inc_min(int* a, int* b, int* c){
  //in increasing order using min_ptr
}

void order_3_dec_max(int* a, int* b, int* c){
  //in decreasing order using max_ptr
}

void order_3_dec_min(int* a, int* b, int* c){
  //in decreasing order using min_ptr
}

Rendre la monnaie

Le but de cet exercice est d’écrire une fonction de rendu de monnaie. La fonction make_change reçoit la valeur due, la quantité d’argent reçue et un buffer pour indiquer quelle quantité de chaque billet/pièce doit être retournée au client.

Par exemple, pour une valeur due de 410 et une valeur reçue de 500, le tableau devrait contenir 1 dans la cellule change[N50] et 2 dans la cellule change[N20] après l’appel à la fonction.

Si le montant reçu est inférieur au prix, la fonction devrait retourner -1 (et 0 si ce n’est pas le cas).

enum note { N500, N200, N100, N50, N20, N10, N5, N2, N1 };
int const values[] = { 500, 200, 100, 50, 20, 10, 5, 2, 1 };

int remove_max_notes(enum note n, int* rest){
  // ...
}

int make_change(int amount, int received, int change[9]){
  // ...
    
  int rest ;

  change[N500] = remove_max_notes(N500, &rest);
  // ...
    
  return 0;
}

La fonction remove_max_notes reçoit une valeur de pièce ou billet et ce qu’il reste à convertir (via un pointeur), supposé être supérieur à 0. Elle calcule le nombre maximal de billets ou pièces de cette valeur pouvant tenir dans le restant, diminue la valeur du restant conformément et retourne ce nombre. La fonction make_change doit ensuite faire usage de cette fonction pour calculer le rendu de monnaie.

Écrire le code de ces fonctions et leur spécification, et prouver la correction. Notons que le code ne devrait pas faire usage de boucles puisque nous ne savons pas encore les traiter.

Triangle

Dans cet exercice, nous voulons rassembler les résultats des fonctions que nous avons écrites dans la section précédente pour obtenir les propriétés de triangles dans une structure. La fonction classify reçoit trois longueurs a, b et c, en supposant que a est l’hypoténuse. Si ces valeurs ne correspondent pas à un triangle, la fonction retourne -1, et 0 si tout est OK. Les propriétés sont collectées dans une structure info reçue via un pointeur.

#include <limits.h>

enum Sides { SCALENE, ISOSCELE, EQUILATERAL };
enum Angles { RIGHT, ACUTE, OBTUSE };

struct TriangleInfo {
  enum Sides sides;
  enum Angles angles;
};

enum Sides sides_kind(int a, int b, int c){
  // ...
}

enum Angles angles_kind(int a, int b, int c){
  // ...
}

int classify(int a, int b, int c, struct TriangleInfo* info){
  // ...
}

Écrire, spécifier et prouver toutes les fonctions.

Notons qu’il y a beaucoup de comportements à lister et spécifier. Écrire une version qui ne requiert pas que a soit l’hypoténuse est possible. Par contre, il pourrait être difficile de terminer la preuve automatiquement avec Alt-Ergo parce qu’il y a vraiment beaucoup de combinaisons à considérer.