C'est toute une histoire : la cryptographie - Partie 1/3

• La GPL, la licence des cornus
• ZdS passe bientôt en version 1.3

Tenter de partager une information avec un groupe restreint de personnes ne date pas des identifiants Facebook, loin de là ! Nous allons voir dans cette petite série d’articles (du nombre de trois) d’où nous sommes partis, et surtout, où nous sommes arrivés. Ce premier article traite uniquement de la période commençant au début de l’Antiquité et finissant à la fin du Moyen Âge.

• L'Antiquité
• Le Moyen Âge
• Sources et liens

L'Antiquité

C’est à l’Antiquité qu’a commencé le chiffrement d’informations. C’est logique : il a bien fallu attendre qu’on ait quelque chose à communiquer avant d’essayer de le dissimuler, non ?

À l’époque, bien entendu, il n’y avait pas d’ordinateurs pour trouver des clés, les appliquer pour chiffrer ou déchiffrer. Il fallait que les spécialistes de l’époque fassent tout à la main. Voyons les méthodes qu’ils ont trouvées.

Il y en a deux sur lesquelles nous allons nous attarder : les méthodes hébraïques et les méthodes grecques. Commençons par les chiffres hébreux.

Les chiffres hébreux

Ce, ou plutôt ces, chiffrements ont été trouvés (on estime) entre le 6^e et le 7^e siècle avant J.-C. Et comme leur nom l’indique, ils ont été trouvés par les Hébreux. Ces méthodes de chiffrement (qui sont au nombre de trois) se nomment Atbash, Atbah et Albam. Commençons par le commencement : attardons-nous sur Atbash. Comme dit précédemment, ce chiffre (ou chiffrement) a été inventé par les Hébreux. Pour ceux ne parlant pas l’hébreu… Déjà, faites un effort que diable !, et ensuite, voici le fameux alphabet hébreu :

Maintenant, voyons en quoi consiste ce chiffrement… Atbash vient des lettres hébraïques Aleph, Tav, Beith et Shin. Si vous regardez l’image que nous venons de vous donner, vous pouvez voir quelque chose d’assez particulier : Aleph et Tav sont respectivement la première et la dernière lettre de cet alphabet. De plus, Beith et Shin sont de même la deuxième et avant-dernière lettre de l’alphabet… Et si votre petit doigt vous dit que ce n’est pas pour rien, il a totalement raison ! Ce chiffrement s’appelle ainsi car cette méthode (primaire certes, mais datant de plus de 2500 ans !) consiste à inverser l’ordre des lettres de l’alphabet. Donc voici l’équivalent de cette table de chiffrement pour notre alphabet.

Nous avons au-dessus la lettre que nous voulons écrire et en dessous la lettre à écrire pour rendre le message incompréhensible. Donc le mot "ZESTEDESAVOIR"¹ devient : "AVHGVWVHZELRI".

Ce qu’il se passe, c’est que la 1^e lettre est envoyée sur la 26^e, la 2^e sur la 25^e, … et la n^e sur la $26 + 1 - n$^e.

Dans la même idée, il y a le chiffrement Albam. Son nom vient des lettres hébraïques Aleph, Lamed, Beith et Mem. Donc dans ce cas-ci, Aleph devient Lamed et Beith devient Mem. Si on l’adapte à notre alphabet, voici ce que l’on obtient :

Si l’on veut chiffrer "ZESTEDESAVOIR" ici, on obtiendra "MRFGRQRFNIBVE".

Ce qu’il s’est passé, c’est que nous avons fait une rotation de l’alphabet de moitié. La première lettre devient le $1+\frac{26}{2} = 14$^e, la deuxième devient la $2+\frac{26}{2} = 15$, … et la n^e devient la $n + \frac{26}{2} = n + 13$^e. Pour ça, il faut qu’on travaille en modulo² : la 16^e devient la $16 + 13 = 29$^e. Mais comme l’alphabet ne contient que 26 lettres, il faut que l’on prenne la 3^e ($= 29 - 26$).

Et enfin, il y a la méthode Atbah. Cette méthode est plus compliquée, bien que le principe reste le même. Dans cette méthode, Aleph est associée à Teth et Beith l’est à Heith. Mais comme vous pouvez le voir, ce ne sont pas deux lettres consécutives. Donc ici, on a toujours une permutation des lettres mais de manière presque aléatoire. Sur notre alphabet, ça donnerait ceci³.

Notre mot "ZESTEDESAVOIR" est ici chiffré en "SNZYNFNZIWMAJ".

Il est par contre plus difficile de déterminer sur quelle lettre est envoyée quelle lettre. Comme dit au-dessus, les lettres sont disposées de manière presque aléatoire. Et attention, nous avons volontairement mis presque en italique pour la simple et bonne raison que c’est aléatoire en apparence mais uniquement en apparence. Cet ordre a une caractéristique qu’ont également les deux autres présentés juste avant. Cette caractéristique est le fait que ces chiffres sont réversibles. Ce mot veut dire que si l’on chiffre une première fois le message (par exemple "ZESTEDESAVOIR" qui devient "SNZYNFNZIWMAJ" avec Atbah) puis que l’on rechiffre ce message déjà chiffré, on obtient "ZESTEDESAVOIR". C’est grâce à cette méthode que les messages étaient déchiffrés. Nous allons prouver ce qui vient d’être dit pour les deux premières méthodes (Atbash et Albam).

Si l’on utilise un procédé pour passer du caractère C₁ (le caractère clair) au caractère C₂ (le caractère chiffré) qui fonctionne de la sorte,

$C_2 = 26 + 1 - C_1$

Imaginons un caractère C₃ qui est le caractère rechiffré. On peut déduire la formule suivante.

$C_3 = 26 + 1 - C_2 = 26 + 1 - (26 + 1 - C_1) = 27 - (27 - C_1) = 27 - 27 -(-C_1) = C_1$

Ce qui nous montre bien qu’en chiffrant le même caractère deux fois d’affilée, on revient au premier. C’était une petite démonstration mathématique, mais vous pouvez également simplement le voir en observant que chaque caractère clair C₁ est chiffré en caractère C₂ et que ce même caractère clair C₂ est chiffré en C₁.

La démonstration mathématique peut s’appliquer au deuxième chiffrement (Albam).

$C_3 = (C_2 + 13) \mod 26 = (((C_1 + 13) \mod 26) + 13) \mod 26 = (C_1 + 26) \mod 26 = C_1$

N’ayant pas de formule toute faite, on ne peut pas le démontrer pour Atbah, mais vous avez compris le principe, vous pouvez regarder la table de conversion.

Maintenant que vous savez que ces méthodes sont réversibles, il est également important de savoir qu’elles étaient rarement utilisées seules. Elles étaient utilisées successivement. C’est ce que l’on appelle le surchiffrement. Cette méthode fut utilisée pendant l’Antiquité mais a continué de servir bien plus tard. Et nous aurons l’occasion d’y revenir.

La Grèce antique

Après avoir parlé des Hébreux, parlons un peu des Grecs. Parlons de la scytale qui date du 5^e siècle avant J.-C. et ensuite de Polybe qui date, quant à lui du 2^e siècle avant J.-C.

La scytale

Commençons par parler de la scytale. La scytale n’était pas réellement un moyen efficace car le message n’était pas réellement chiffré, il était juste transposé. Comme vous pourrez le voir sur l’image qui suit, une bandelette (habituellement un papyrus ou une lanière de cuir) était enroulée autour d’un bâton d’un certain diamètre et la personne chiffrant le message écrivait sur le papier enroulé. Ensuite, le papier était déroulé pour être envoyé, et il fallait à la personne chargée de le lire un bâton de même diamètre que celui de l’expéditeur pour que ce soit possible. Autrement, la permutation ou le décalage risque très fortement d’être erroné.

Sur l’image ci-dessus, on voit le message en train d’être écrit autour du bâton, et sur l’image ci-dessous, on voit le papier en train d’être déplié avec les caractères qui se suivent sans avoir de sens direct (ici d’autant plus que le mot est écrit en cyrillique, ce que nous ne pourrions vous traduire…).

Cet instrument est également appelé scytale spartiate. On ne sait pas si ce sont les spartiates qui l’ont inventé. Par contre on sait qu’ils s’en sont servi, entre autres pour préparer la célèbre bataille de tentative d’invasion par Phranabaze, roi des Perses, contrée par Lysandre, roi des Spartiates lui-même averti par un de ses soldats ramenant une scytale.

Polybe

Faisons un saut de presque 300 ans et parlons de Polybe. Polybe était un citoyen grec au 2^e siècle avant J.-C. et est l’inventeur du carré de Polybe. Ce carré fonctionne de la sorte : on fait un carré avec 5 lignes et 5 colonnes. Ensuite, on remplit chacune de ces cases par une lettre. En français, il est usuel de supprimer le W qui est couplé avec le V. On peut donc imaginer un tableau comme le suivant en français.

Une fois ce tableau fait, il ne reste plus qu’à déterminer les deux chiffres étant liés à chaque lettre. Par exemple, si l’on veut chiffrer la lettre 'Z’, on se place sur la bonne ligne (5) et puis sur la bonne colonne (5 aussi). Donc la lettre 'Z' se chiffre 55. Si vous voulez chiffrer 'E’, vous vous placez sur la bonne ligne (la 1) et sur la bonne colonne (5). 'E' correspond donc à 15. Si on continue pour chiffrer "ZESTEDESAVOIR", on obtient la suite de nombre suivante : 55 15 44 45 15 14 15 44 11 52 35 24 43.

Cette méthode n’est pas bien compliquée et peut être assez efficace si on truque le tableau. Par exemple, on utilise une clé pour décaler le début de notre tableau. Donc si notre clé est 7, la première case est H (A + 7 = 8 = H) et plus A. Le tableau complet avec une clé de 7 est le suivant.

Il y a moyen d’encore plus truquer le tableau si l’on décide de mettre un mot de passe plutôt qu’une clé. Si l’on décide de mettre "POLYBE" comme mot de passe, notre tableau devient :

On a donc placé le mot de passe au début, puis on a écrit l’alphabet en faisant bien attention de ne pas réécrire une lettre apparaissant déjà dans le tableau.

Bien évidemment, il nous reste toujours la possibilité de combiner les deux pour un chiffrement encore plus efficace (souvenez-vous du surchiffrement vu au chapitre précédent) !

Le chiffrement de César

Il est impossible de parler de cryptographie sans parler du chiffrement de César. Mais attention, s’il est important de rendre à César ce qui appartient à César, il est également important de lui reprendre ce qui ne lui appartient pas !

Le chiffrement de César est basé sur la substitution des caractères dans l’alphabet. Ça vous dit quelque chose ? C’est normal, on vient d’en parler : il s’agit d’une forme dérivée des chiffres hébreux, 500 ans plus tôt. Nous vous rappelons que le chiffre Albam était un décalage de longueur fixe (et égale à la moitié de la longueur de l’alphabet), alors que le chiffrement de César était un décalage de longueur variable appelée clé de substitution. Nous n’allons donc pas nous attarder là-dessus car nous avons déjà vu ces méthodes, mais il était impératif d’en parler car c’est actuellement bien souvent par ce nom qu’est désignée n’importe quelle méthode de substitution de caractère par une clé fixée.

La raison pour laquelle on donne ce nom est simple : ce n’est pas César le premier à avoir pensé à cette méthode, mais on sait qu’il en a largement fait usage pour faire circuler, entre autres, les consignes destinées à ses généraux. Étant la personne qui a le plus informé les historiens quant à ce procédé, c’est son nom qui a été retenu. Exactement comme pour la scytale spartiate.

Le Moyen Âge

L’Antiquité étant terminée, passons plus que rapidement sur le Moyen Âge qui s’est avéré être peu fructueux sur l’avancée de la cryptographie. Il est cependant important de parler d’Alberti qui a introduit une nouvelle notion : le chiffre polyalphabétique. Derrière ce nom bizarre, que se cache-t-il ? C’est ce que nous nous apprêtons à voir.

Alberti et le chiffre polyalphabétique

Alberti (Leon Battista de son ses prénoms) a été l’inventeur, au 15^e siècle après J.-C., du chiffre polyalphabétique. Alors premièrement, ne vous affolez pas, on vient de faire un bond de 1000 ans en avant, mais comme nous l’avons dit juste avant, on a un peu stagné pendant quelques années…

Ensuite, qu’est-ce qu’un chiffrement polyalphabétique ? C’est un chiffrement qui change de clé pendant la phase de chiffrement ou celle de déchiffrement. Alberti a instauré cela à l’aide d’un cadran un peu particulier dont voici une représentation.

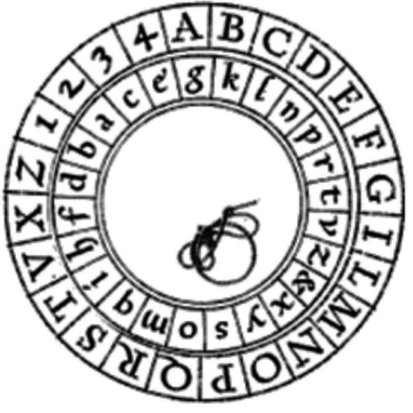
Ce cadran est composé d’un disque fixe à l’extérieur contenant 20 lettres (H, K et Y sont volontairement omis et J, U et W ne faisaient pas partie de l’alphabet latin d’Alberti) et 4 chiffres ainsi que d’un disque rotatif à l’intérieur contenant les mêmes 20 lettres auxquelles s’ajoutent H, K, Y et le symbole &¹. Le principe est le suivant : pour chiffrer un message, il faut placer le disque rotatif dans une configuration initiale. Ensuite, on lit 3 (ou 4 en fonction des sources) caractères du message que l’on chiffre en prenant l’équivalent du disque fixe sur le disque rotatif, puis on fait une rotation du disque d’un nombre arbitraire, et on recommence jusqu’à ce que le message ait été codé en entier. Certes, c’est déjà un peu plus compliqué (surtout à expliquer !) mais attendez que nous développions un peu.

Chiffrons notre éternel "ZESTEDESAVOIR" en commençant avec la disposition de l’image (le A en clair correspond au G chiffré) et en lisant 4 caractères avant chaque rotation de 1. Découpons tout d’abord notre message en blocs de longueur 4 : "ZEST", "EDES" "AVOI", "R". Effectivement, le dernier bloc ne fait pas 4 caractères mais ça n’est pas important. Chiffrons tout d’abord le premier des blocs, donc transformons "ZEST" en "DPQI". Pour savoir comment substituer les lettres, il vous suffit de regarder sur l’image. Maintenant, décalons le disque rotatif d’une case vers la gauche (dans le sens trigonométrique ou sens antihoraire pour ceux qui attrapent de l’urticaire en lisant le terme "trigonométrie" ). Nous avons donc le K qui a pris la place du G en dessous de la lettre A comme vous pouvez le voir sur l’image suivante.

Il nous faut maintenant chiffrer "EDES" avec la nouvelle version du cadran. Le procédé est toujours le même, voici ce que vous devez obtenir : "RPRI". Si vous continuez ceci, vous devez obtenir les blocs suivants.

Ce qui nous montre que le message "ZESTEDESAVOIR" une fois chiffré est "DPQIRPRITDO&H".

C’est tout pour cette première partie. Il est volontaire de faire des articles relativement courts afin de rassembler les méthodes de chiffrement étant liées entre elles même s’il faut en faire paraître plusieurs. Cela évite l’indigestion et surtout, cela permet d’avancer progressivement (histoire de ne pas vous perdre en chemin ).

Rendez-vous au prochain épisode pour la suite de l’histoire !

Sources et liens

Pour aller plus loin :

• pour les chiffres hébreux : voici une page explicative ;
• concernant le carré de Polybe, l’article de Wikipédia peut nous informer (notez qu’il peut être intéressant de lire l’article anglais pour voir que si en français on a tendance à fusionner V/W, les anglophones préfèrent fusionner I/J par exemple) ;
• à propos de la Scytale : autre exemple sur Wikipédia, exemple plus complet (anglais), explication supplémentaire ;
• et enfin pour Alberti et le chiffre polyalphabétique : plus d’explications avec essai.

• La GPL, la licence des cornus
• ZdS passe bientôt en version 1.3