De nos jours, il est facile de savoir où l’on est. Grâce au GPS ou à des systèmes concurrents, connaître précisément sa position est devenu un jeu d’enfant. Les récepteurs GPS sont d’ailleurs partout, que ce soit dans les téléphones, les voitures, les avions, ou encore les bateaux.
Pourtant, le GPS ne répond pas à tous les besoins. Pour certaines applications, il est trop cher, trop peu précis, ou tout simplement impossible à mettre en œuvre. Par exemple, pour les sous-marins en plongée, il n’est pas possible de capter les signaux du GPS. Sur un champ de bataille, le positionnement doit rester précis même en cas de brouillage. Sur les systèmes grand public, les contraintes de coût limitent encore la précision.
Quand le GPS seul n’est pas une option viable, on recourt souvent à la navigation inertielle. Cette technique permet d’estimer le déplacement d’un objet avec seulement un capteur d’accélération et un chronomètre. Cet article en présente le principe de fonctionnement.
Principe physique
La navigation inertielle est rendue possible grâce aux lois physiques régissant le mouvement des corps, car elles permettent de déterminer la position d’un objet en connaissant seulement :
- le point de départ,
- la vitesse initiale,
- l’accélération à chaque instant,
- le temps écoulé depuis le départ.
Pour simplifier, nous considérons un mouvement sur une seule dimension seulement (par exemple l’axe des abscisses), mais sachez que les cas à deux et trois dimensions sont identiques.
On part de la définition de l’accélération. Il s’agit de la dérivée de la vitesse par rapport au temps :
On en déduit une expression de la vitesse par intégration :
La vitesse est, par définition, la dérivée de la position par rapport au temps :
On procède alors à une deuxième intégration pour en déduire la position en fonction de la vitesse :
Si on réunit tous les morceaux, on obtient :
En fin de compte, la position est exprimée en fonction des éléments qu’on s’est donné au départ : la position initiale, la vitesse initiale et l’accélération jusqu’à l’instant .
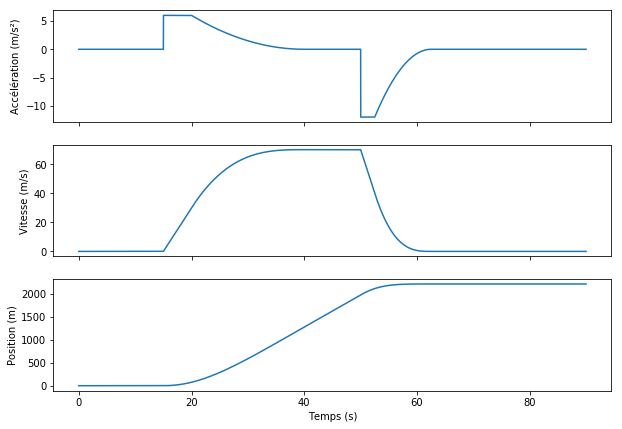
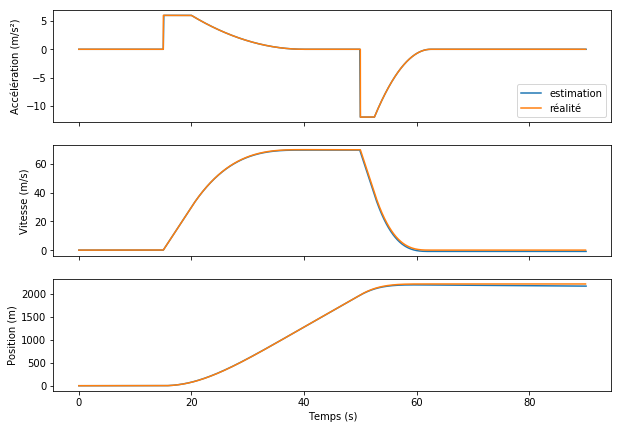
Illustrons ce principe physique par un exemple. Imaginez une voiture de sport sur une piste rectiligne, et qui enchaîne les cinq phases suivantes :
- une phase sans accélération pendant 15 secondes,
- une phase d’accélération pendant les 25 secondes suivantes,
- une nouvelle phase sans accélération pendant les 10 secondes suivantes,
- une phase de freinage pendant 12,5 secondes,
- une nouvelle phase sans accélération à la fin.
Avec les expressions précédentes, on peut déduire la vitesse, puis la position à partir de l’accélération. La figure ci-dessous montre le résultat qu’on obtient pour notre exemple.
Mise en œuvre
Les lois physiques vues ci-avant peuvent être simulées en temps réel par un calculateur, en utilisant des techniques d’intégration numérique.
Nous utilisons ici la méthode d’Euler, qui est certainement la technique la plus simple. D’autres approches plus raffinées existent, mais elles ne sont pas utiles pour notre article.
Le cœur de la méthode d’Euler, dans notre cas, consiste à approximer le taux de variation entre deux instants suffisamment proches par la dérivée.
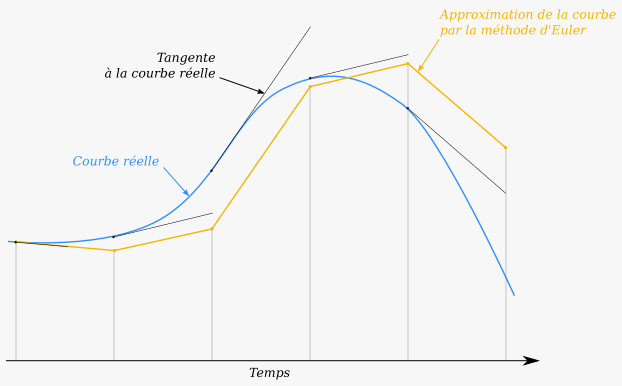
En appliquant cette approximation dans notre cas, on déduit deux récurrences : une pour mettre à jour la vitesse, et une pour mettre à jour la position. Notez qu’on travaille toujours sur une seule dimension par simplification, mais qu’on pourrait aisément généraliser à trois dimensions.
Le calcul se déroule de la manière suivante1. On part d’une estimation de position initiale et de vitesse initiale . Ensuite, à chaque instant où l’on souhaite estimer la position, on commence par mettre à jour l’estimation de vitesse :
Après, on met à jour l’estimation de position :
Et on recommence à un nouvel instant en partant de l’estimation précédente.
Pour que la méthode d’Euler estime suffisamment bien la véritable intégrale, il faut que les instants soient suffisamment proches les uns des autres, c’est-à-dire que la fréquence de mise à jour soit suffisamment élevée.
Reprenons notre voiture de sport de la section précédente et estimons sa position avec les calculs vus ci-avant. Le résultat est montré dans la figure ci-dessous. La réalité physique et l’estimation sont presque indiscernables !
- On travaille toujours sur une seule dimension, comme dans la première section, mais les calculs pour les autres dimensions sont identiques.↩
Sources d'erreur
La section précédente fait une démonstration de la navigation inertielle dans un cas idéalisé. En pratique, différents phénomènes introduisent des erreurs dans le processus d’estimation.
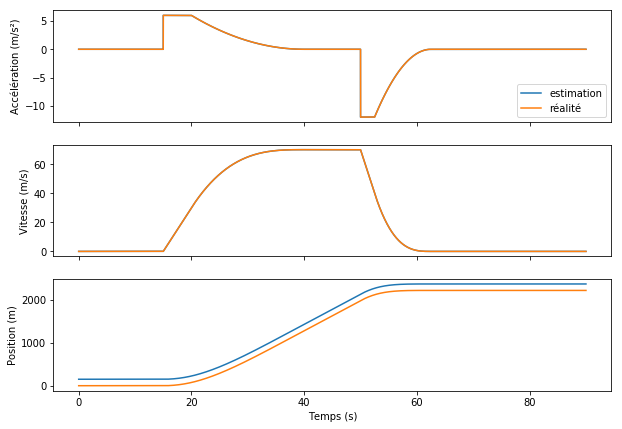
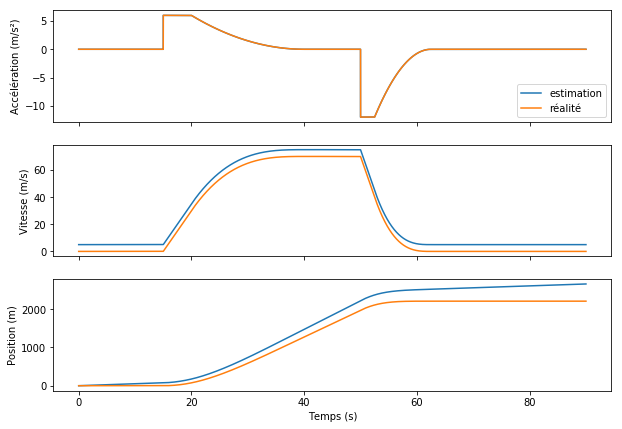
Erreur sur les conditions initiales
Les conditions initiales, position et vitesse, sont souvent issues de mesures, entachées d’erreur plus ou moins importantes.
Par exemple, en mer, un bateau pourrait se repérer en utilisant les étoiles, mais les instruments de mesure n’étant pas parfaitement précis, la position ne serait connue que de manière approximative.
De même, toutes sortes d’instruments permettent de mesurer la vitesse avec une erreur variable.
L’erreur de position initiale créée un décalage entre l’estimation et la réalité, qui va perdurer indéfiniment. L’erreur de vitesse initiale, quant à elle, fait dériver l’estimation, en introduisant un décalage qui croît proportionnellement avec le temps, rendant à terme l’estimation inutile.
Erreur d’intégration numérique
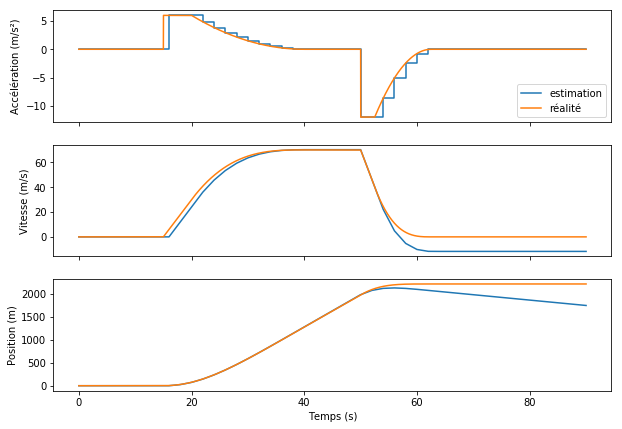
La méthode d’intégration numérique introduit des erreurs qui grandissent à mesure que la fréquence de mise à jour diminue. Ce phénomène s’explique par le fait que l’approximation du taux d’accroissement devient de moins en moins bonne quand la fréquence de la mise à jour diminue.
En pratique, les calculateurs modernes permettent une précision respectable. Cependant, si on attend suffisamment longtemps, cette erreur finira toujours par se manifester sensiblement.
L’exemple ci-dessous reprend le cas de la voiture de sport. Cette fois-ci, la fréquence de mise à jour est beaucoup plus faible, et crée des erreurs qui s’accumulent au cours du temps. Pour que le phénomène soit bien visible, la fréquence de mise à jour est choisie volontairement très basse.
Erreur de mesure d’accélération
L’erreur la plus gênante en pratique est sans doute celle sur la mesure d’accélération.
Les capteurs d’accélération présentent différents types d’erreurs liés à la constitution et à la chaîne de traitement du signal. On peut notamment citer le biais, le bruit de mesure, ou les non-linéarités.
Bien qu’on puisse les limiter, ces erreurs sont inévitables et entraînent une dérive à mesure que l’estimation prend en compte le bruit comme s’il s’agissait d’une véritable mesure.
L’exemple ci-dessous montre comment la dérive affecte l’estimateur de position de notre voiture. La voiture est immobile, mais un bruit entraîne la dérive de l’estimateur, que j’aime appeler le « voyage immobile ». :-)
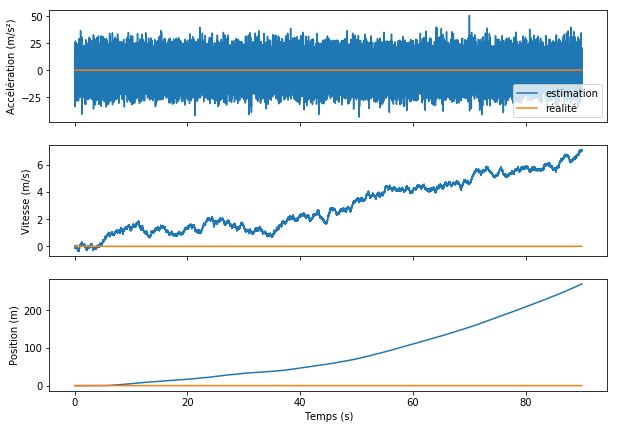
Il existe encore d’autres erreurs spécifiques à certaines applications, qui ne seront pas traitées dans cet article.
Mitigation des erreurs
Il existe différentes techniques pour mitiger les erreurs.
Erreur de position et vitesse initiale et initialisation
Pour mitiger l’erreur de position et de vitesse initiales, il est possible d’effectuer l’initialisation dans des conditions précises connues. Par exemple, pour un véhicule terrestre, il s’agirait de faire une mesure à l’arrêt (vitesse nulle) en un point précisément mesuré (erreur de position faible).
Ce n’est pas toujours possible, si on ne peut pas se mettre à l’arrêt ni savoir précisément où l’on est. C’est le cas notamment pour un bateau en pleine mer : le courant et le vent empêchent de mesurer la véritable vitesse, c’est-à-dire la vitesse par rapport au fond et la précision de la position initiale est limitée par les moyens du bord.
Erreur d’intégration et puissance du calculateur
Nous avons vu dans la partie précédente que si on mettait à jour l’estimation trop lentement, l’erreur de position s’accumulait. Pour limiter ce type d’erreur, il suffit alors de procéder plus vite.
La performance du calculateur peut devenir bloquante. D’une part, les contraintes de coûts limitent la puissance des calculateurs dans les applications grand public (dans un téléphone par exemple) ; d’autres part, plus les accélérations maximales du véhicule sont importantes et le positionnement nécessaire précis, plus la mise à jour doit se faire vite (dans un avion de chasse par exemple), ce qui peut devenir limitant pour du calcul en temps réel.
Erreur de mesure, filtrage et fusion de capteurs
Les erreurs de mesure sont vraiment les plus gênantes, car elles sont à la longue la principale cause de dérive. Pour les applications exigeantes, les ingénieurs travaillent sur des capteurs très précis et robustes qui limitent fortement les erreurs (par exemple basés sur de l’interférométrie laser).
Mais même les meilleurs capteurs ne peuvent éviter totalement la dérive, il suffit d’attendre suffisamment longtemps pour que l’erreur devienne arbitrairement grande. C’est pourquoi on a recours à des techniques où l’on mélange l’information de différents capteurs.
Un cas typique est de mélanger l’estimation inertielle avec une mesure de position par satellite, comme le GPS. Cela permet d’éliminer la dérive, tout en ayant une précision supérieure à celle de chaque capteur pris séparément. La figure montre un exemple de telle mélange ; il utilise une technique simpliste mais illustre bien le principe : l’estimation combinée est meilleure que le GPS seul et sans dérive.
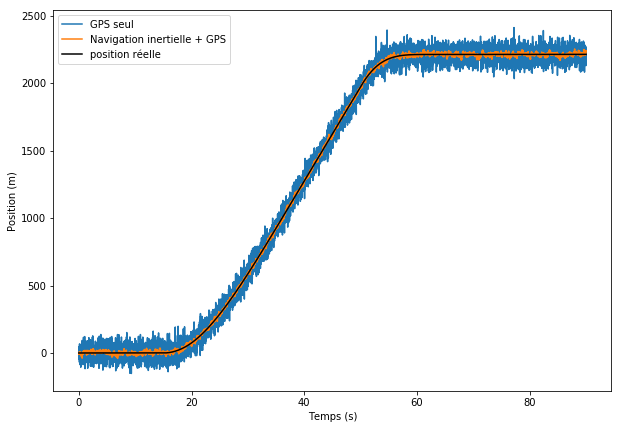
Une technique usuelle non simpliste est le filtrage de Kalman. Cette technique permet de réaliser un filtre qui mélange de manière optimale (selon certains critères) les informations obtenues par navigation inertielle et par mesure de position, en prenant en compte les erreurs du modèle physique et les erreurs de mesure.
Et voilà pour cette introduction ! Vous avez vu dans le principe général de la navigation inertielle. Si vous souhaitez découvrir ce domaine plus en détail, sachez qu’il y a énormément de spécificités pratiques à découvrir, telles que la prise en compte de la gravité terrestre, de la rotondité de la Terre et toutes les autres subtilités nécessaires à la mise en pratique industrielle de la navigation inertielle.
Références
- Article Navigation inertielle sur Wikipédia,
- Article Centrale à inertie sur Wikipédia,
- Article Calcul numérique d’une intégrale sur Wikipédia,
- Article Kalman Filtering sur Wikipedia (en anglais),
- Notes du cours Introduction au filtre de Kalman.
Remerciements
Merci à Dwayn pour les relectures en bêta et à adri1 pour la validation.
Illustration de la miniature : Carte du monde faite à partir des données de Natural Earth (projection: planisphère Hölzels centrée 10° est), par Ktrinko, sous licence CC BY-SA 3.0.