De l'importance des qualifications au Grand Prix de Monaco

Analyse de de données en Formule 1

Il y a quelques semaines se déroulait le Grand Prix de Monaco de Formule 1. À cette occasion, j’ai entendu dire dire que les qualifications y jouent un rôle prépondérant, car il y est difficile de doubler. Quoi de mieux que de vraies données pour tenter de vérifier cela ?

Trouver des données

Les données de la Formule 1 sont relativement faciles à trouver, mais pas toujours sous une forme correcte.

On notera en particulier que Wikipédia comporte quasiment tous les résultats, notamment la grille de départ (conséquence directe des qualifications modulo les pénalités) et le résultat de la course. C’est ce que j’ai utilisé au tout début pour explorer un peu les données et faire une preuve de concept avec un tableau.

Le mieux serait peut-être d’utiliser le site officiel de la discipline, qui contient une archive de tous les résultats qui m’intéressent, mais il n’est pas utilisable directement. Pour l’utiliser, il faut en extraire les données. Ce que j’ai retenu de faire.

Il existe aussi des jeux de données bien présentés, certains sites nécessitent une inscription et d'autres sont suffisamment mal référencés pour que je les trouve après avoir commencé à travailler les données (trop tard pour changer de plan)… J’aurai probablement utilisé ce deuxième site si je l’avais trouvé avant.

Il y a même des sites souvent commerciaux qui proposent même des API pour recevoir tout plein de données en quasi-temps réel et qui ont une granularité qui va jusqu’au tour par tour !

Ma boîte à outils

Comme dit plus haut, j’ai choisi d’extraire les données depuis le site officiel de la Formule 1.

J’ai procédé avec ce qui semblait le plus facile d’accès pour moi :

  • Python, mon langage de prédilection ;
  • urllib pour récupérer le contenu des pages web ;
  • lxml pour extraire les données des pages, avec en particulier la possibilité de faire des requêtes XPath que j’avais déjà utilisées par ailleurs et qui sont très pratiques ;
  • matplotlib pour regarder des jolis graphiques ;
  • numpy pour calculer sur mes données le cas échéant.

Traitement des données

La partie la plus pénible et que je n’ai pas eu le courage d’automatiser est la récupération des URL intéressantes. Je l’ai fait à la main et me suis limité à une quarantaine de pages en tout, pour que cela reste pratiquable. Il y a sûrement moyen de le scripter en observant la structure des pages, mais ce n’était pas l’intérêt premier de mon exploration.

À partir de là, j’ai réalisé un script qui :

  • télécharge les pages web ;
  • extrait les données des pages web (position, nom du pilote, etc.) ;
  • traite les données pour en sortir les infos qui m’intéressent (voir la partie suivante) ;
  • affiche ces données pour les humains.

Il n’y a normalement là rien d’incroyable pour un développeur expérimenté, mais ce n’est pas vraiment mon cas, et j’ai appris plein de choses (en particulier tout ce qui touche au scraping) et ai aussi eu une piqûre de rappel sur d’autres choses (XPATH).

Résultats de l'analyse

Je n’ai pas passé trop de temps à réfléchir et ai opté pour l’approche qui consiste à analyser la relation entre la position de départ et d’arrivée.

Probabilité d’arriver x-ième en partant de la y-ième place

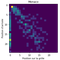
Quand on dit que les qualifications sont importantes, c’est une manière de dire qu’il sera difficile de remonter dans le classement au cours de la course. Une manière de quantifier ça, c’est de regarder pour chaque position de départ la probabilité d’arriver à une position d’arrivée donnée. Tout cela forme une matrice, où l’élément à la colonne i et la ligne j est la probabilité d’arriver à la j-ième place en partant de la i-ème position sur la grille de départ.

Le calcul est fait à l’aide des données des dix derniers Grand Prix.

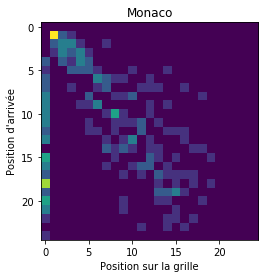
Matrice pour Monaco
Matrice pour Monaco.
(Dans cette matrice, la colonne de gauche correspond aux pilotes non-classés).

Avec ça tout seul, on n’ira pas très loin, aussi j’ai décidé de comparer avec une course réputée pour ses dépassements nombreux : le Grand Prix de Chine. On utilise toujours les dix derniers grands prix.

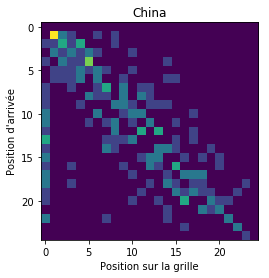
Matrice pour Monaco
Matrice pour la Chine.

Les deux matrices sont assez différentes, c’est intéressant ! Alors, à l’œil nu, je remarque des choses :

  • dans les deux cas, celui qui part premier à plus de chance d’arriver premier (la corrélation est toute trouvée : être un bon pilote dans une bonne voiture conduit à être le plus rapide en qualification et en course).
  • le Grand Prix de Monaco semble être ramassé à la tête (en gros la tête de course est globalement figée) et éclatée vers la fin, avec pas mal de non-classés (abandons par exemple) ;
  • le Grand Prix de Chine présente une grosse bande large, qui signifie qu’on peut relativement facilement gagner et perdre quelques places quelle que soit la position de départ.

Mesure de diagonalité

Si on imagine une course sans possibilité de dépasser la matrice serait diagonale. Si on arrive à mesurer la diagonalité d’une matrice, on pourrait alors quantifier la facilité de dépassement sur une course !

J’ai eu un peu de mal à trouver les bons mots-clés pour ma recherche, mais j’ai fini par trouver une méthode intéressante. On a un score de diagonalité r. Grossièrement, plus r est proche de 1, plus la matrice est diagonale. Plus r est proche de zéro, moins c’est le cas. Statistiquement, c’est un genre de corrélation entre les différents vecteurs ligne et colonne.

Pour la matrice complète, on trouve :

  • r = 0.364 pour Monaco ;
  • r = 0.609 pour la Chine.

C’est l’inverse de l’attendu ! Essayons d’éliminer le nombre d’abandons qui semble grand à Monaco de l’équation en retirant la première colonne (et ligne) :

  • r = 0.796 pour Monaco ;
  • r = 0.818 pour la Chine.

Ce coup-ci, c’est plus proche, mais on a peut-être juste trouvé la valeur globale pour un Grand Prix de Formule 1, où la qualification est de toute façon importante, quel que soit le circuit. Si on s’intéresse seulement à la tête de course, on a pour le carré des cinq premiers :

  • r = 0.679 pour Monaco ;
  • r = 0.457 pour la Chine.

Ah ! Quelque chose qui correspond à ce qu’on voit graphiquement. Ces deux valeurs signifient que pour la tête de la course, le résultat à Monaco est plus dépendant de la qualification que pour la Chine.

Cet indicateur (comme l’espérance par exemple) est trop synthétique : on perd une partie de l’information, et la précaution doit être de mise dans sa manipulation.

Alors, les qualifications sont-elles plus importantes à Monaco qu’ailleurs (en Chine en l’occurrence) ? Oui, mais seulement quand on ne considère que la tête de course. Pour le reste, c’est plus incertain.

Les données de la Formule 1 (et d’autres sports) regorgent d’informations cachées (sauf peut-être des parieurs professionnels), et je pourrai encore y passer des heures. Heureusement, le reste de ma vie me rappelle à la réalité.

10 commentaires

Ah un article intéressant sur la F1. Mon sport favori. :D

Il y a un autre site intéressant pour avoir des statistiques et résultats fiables sur la F1 : https://www.statsf1.com/

Sinon dans l’analyse tu oublies quelques éléments. Par exemple la météo. Il semble que Monaco n’a été courue sous la pluie qu’en 2016 ces dernières années (et encore, pas très longtemps) alors que la Chine a eu au moins deux courses intégrales dans ces conditions en 2009 et 2010. Du fait que la pluie lisse les performances des voitures entre elles et du risque accrue d’accidents ou d’erreurs, les dépassements sont de fait plus nombreux.

Tu ne tiens pas compte des écarts de performance théoriques entre les voitures (difficile à évaluer ceci-dit). Quand Verstappen est parti dernier à Monaco en 2018, même si c’est dur de remonter, sa voiture lui permet de le faire de manière régulière. S’il s’était qualifié devant comme cela aurait dû être le cas, il n’aurait probablement pas pu progresser dans la hiérarchie.

Il faudrait en tenir compte pour ne pas favoriser une piste plutôt qu’une autre selon ces critères.

Ensuite oui, plus on est au fond du classement, plus le résultat est volatile. Déjà car la probabilité d’un abandon devant soit augmente quand on recule dans la grille, ce qui favorise la remontée dans le classement. Puis quand tu n’as rien à perdre, il est plus facile de tenter des manœuvres ou des stratégies osées qu’à l’avant du peloton.

Sans compter finalement aussi l’écart de performances. Depuis 2014, les 6 premières places sont presque comme verrouillées, et les écarts entre ces 6 pilotes est assez grand ce qui ne favorise pas les changements en cours de grand prix.

+1 -0

je me demande à quel point un petit SVM voire un simple arbre de décision serait pertinent ici : prédire la place en fonction de :

  • nom du grand prix
  • place en qualif
  • condition météo

avec le logiciel orange on pourraît même visualiser le critère le plus important en fonction du grand prix.

+2 -0

Pour ce qui est de faire du prédictif, je laisse ça aux spécialistes, pour ma part, je n’ai pas envie de passer plus de temps sur le sujet. :)

J’aurai bien aimé que tu partages ton code pour que l’on puisse en profiter aussi.

firm1

C’est l’export d’un notebook Jupyter. Ça faut ce que ça vaut…

# coding: utf-8

# # 1 Collecter les données
# 
# Pour collecter les données :
# 1. récupérer les URL souhaitées ;
# 2. récupérer les données brutes depuis les URL ;
# 3. extraire les informations utiles.

# ## 1.1 Récupérer les URL souhaitées
# 
# Les URL sont récupérées manuellement, il suffit ici de les charger.
# 
# Il existe deux groupes d'URL correspondant à deux données différentes : les résultats de la course et la position sur la grille de départ.

# In[20]:

races = ['monaco', 'shanghai']
datatypes = ['grid', 'result']


# In[21]:

def load_urls(filename):
    with open(filename) as f:
        return f.readlines()
    
def filename(race, datatype):
    file_format = "urls_{}_{}.txt"
    return file_format.format(race, datatype)


# In[22]:

urls = {}
for r in races:
    urls[r] = {}
    for t in datatypes:
        urls[r][t] = load_urls(filename(r, t))


# In[23]:

urls


# ## 1.2 Récupérer les données depuis les URL

# In[24]:

import urllib.request as req


# In[27]:

def load_pages(urls):
    pages = []
    for url in urls:
        with req.urlopen(url) as f:
            pages.append(f.read().decode("utf-8"))
    return pages


# In[26]:

pages = {}
for r in races:
    pages[r] = {}
    for t in datatypes:
        pages[r][t] = load_pages(urls[r][t])


# ## 1.3 Extraire les informations utiles

# In[28]:

from lxml import etree
from io import StringIO


# In[29]:

def load_data(page, datatype):
    if datatype == 'grid':
        return load_grid_data(page)
    else:
        return load_result_data(page)

def load_grid_data(page):
    parser = etree.HTMLParser()
    document_tree = etree.parse(StringIO(page), parser)
    # retourne les lignes du tableau de données
    table_lines = document_tree.xpath("//table[@class='resultsarchive-table']/tbody/tr")
    records = []
    for l in table_lines:
        cells = l.xpath("child::*") # retourne les cellules de la ligne
        # il y a 7 cellules
        # la première et la dernière sont du remplissage et donc ignorées
        # les autres contiennent : position, numéro permanent, infos du pilote, voiture, meilleur temps
        record = {}
        record['position'] = cells[1].text
        record['number'] =  cells[2].text
        pilot_information = cells[3].xpath("child::*") # (prénom/nom/nom court)
        record['pilot_name'] = pilot_information[0].text + ' ' + pilot_information[1].text
        record['pilot_shortname'] = pilot_information[2].text
        record['car'] =  cells[4].text
        record['time'] =  cells[5].text
        records.append(record)
    return records

def load_result_data(page):
    parser = etree.HTMLParser()
    document_tree = etree.parse(StringIO(page), parser)
    # retourne les lignes du tableau de données
    table_lines = document_tree.xpath("//table[@class='resultsarchive-table']/tbody/tr")
    records = []
    for l in table_lines:
        cells = l.xpath("child::*") # retourne les cellules de la ligne
        # il y a 9 cellules
        # la première et la dernière sont du remplissage et donc ignorées
        # les autres contiennent : position, numéro permanent, infos du pilote, voiture, nombre de tours, temps, points
        record = {}
        record['position'] = cells[1].text
        record['number'] =  cells[2].text
        pilot_information = cells[3].xpath("child::*") # (prénom/nom/nom court)
        record['pilot_name'] = pilot_information[0].text + ' ' + pilot_information[1].text
        record['pilot_shortname'] = pilot_information[2].text
        record['car'] =  cells[4].text
        record['laps'] = cells[5].text
        record['time'] =  cells[6].text
        record['points'] = cells[7].text
        records.append(record)
    return records


# In[31]:

data = {}
for r in races:
    data[r] = {}
    for t in datatypes:
        data[r][t] = []
        for p in pages[r][t]:
            data[r][t].append(load_data(p, t))


# In[33]:

data


# # 2 Traiter les données
# 
# 1. Extraction des couples (position de départ, position d'arrivée)
# 2. Calcul de la matrice de probabilité

# ## 2.1 Extraction des couples (départ, arrivée)

# In[38]:

def extract_pairs(race_data):
    start = []
    finish = []
    for i in range(len(race_data['grid'])):
        result_list = race_data['grid'][i]
        for record in result_list:
            start.append(record['position'])
            pilot_no = record['number']
            for r in race_data['result'][i]:
                if r['number'] == pilot_no:
                    finish.append(r['position'])
                    break
    return start, finish
        


# In[83]:

start = {}
finish = {}
for r in races:
    start[r], finish[r] = extract_pairs(data[r])


# ## 2.2 Calcul de la matrice de probabilité

# In[57]:

def compute_matrix(start, finish):
    matrix = [[0 for i in range(25)] for j in range(25)]
    denom = 0
    for i in range(len(start)):
        if start[i] == '1':
            denom += 1
        if start[i] == 'NC':
            idx_start = 0
        else:
            idx_start = int(start[i])
        if finish[i] == 'NC':
            idx_finish = 0
        else:
            idx_finish = int(finish[i])
        matrix[idx_start][idx_finish] += 1

    for i in range(len(matrix)):
        for j in range(len(matrix)):
            matrix[i][j] = matrix[i][j]/denom
    return matrix


# In[61]:

matrix = {}
for r in races:
    matrix[r] = compute_matrix(start[r], finish[r])


# # 3 Présenter les données

# In[64]:

import matplotlib.pyplot as plt


# In[80]:

def plot_matrix(matrix, legend):
    plt.imshow(matrix)
    plt.xlabel("Position sur la grille")
    plt.ylabel("Position d'arrivée")
    plt.title(legend)
    plt.show()


# In[81]:

plot_matrix(matrix['monaco'], 'Monaco')


# In[82]:

plot_matrix(matrix['shanghai'], 'China')


# # Mesure de diagonalité

# In[103]:

import numpy as np


# In[144]:

def diag_measure(matrix):
    d = len(matrix)
    j = [1]*d
    r = [i for i in range(1, d+1)]
    r2 = [i*i for i in range(1, d+1)]
    n = np.matmul(np.matmul(j, matrix), np.transpose(j))
    sx = np.matmul(np.matmul(r, matrix), np.transpose(j))
    sy = np.matmul(np.matmul(j, matrix), np.transpose(r))
    sx2 = np.matmul(np.matmul(r2, matrix), np.transpose(j))
    sy2 = np.matmul(np.matmul(j, matrix), np.transpose(r2))
    sxy = np.matmul(np.matmul(r, matrix), np.transpose(r))
    r = (n * sxy - sx * sy)/(np.sqrt(n * sx2 - sx*sx) * np.sqrt(n * sy2 - sy*sy))
    return r


# In[181]:

diag_measure(matrix['monaco'])


# In[146]:

diag_measure(matrix['shanghai'])


# In[147]:

diag_measure([[1, 0], [0, 1]])


# In[174]:

def reduce_matrix(matrix):
    matrix_red = [[0 for i in range(len(matrix)-1)] for j in range(len(matrix)-1)]
    for i in range(len(matrix_red)):
        for j in range(len(matrix_red)):
            matrix_red[i][j] = matrix[i+1][j+1]
    return matrix_red

def reduce_x(matrix, x):
    matrix_red = [[0 for i in range(x)] for j in range(x)]
    for i in range(len(matrix_red)):
        for j in range(len(matrix_red)):
            matrix_red[i][j] = matrix[i+1][j+1]
    return matrix_red


# In[175]:

diag_measure(reduce_matrix(matrix['monaco']))


# In[176]:

diag_measure(reduce_matrix(matrix['shanghai']))


# In[179]:

diag_measure(reduce_x(matrix['monaco'],5))


# In[180]:

diag_measure(reduce_x(matrix['shanghai'],5))


# In[ ]:
+0 -0

En l’etat, l’analyse ressemble plus a un Lapalissade. Ton hypothese c’est "Quand on dit que les qualifications sont importantes, c’est une manière de dire qu’il sera difficile de remonter dans le classement au cours de la course." et tu pretends la valider par les donnees en regardant "pour chaque position de départ la probabilité d’arriver à une position d’arrivée donnée."

J’ai un hypothese moins couteuse, a savoir un facteur de confusion evident: plus tu es bon, et plus tu as une probabilite de finir a une bonne place aux qualifications mais aussi a la course.

De sorte que ton analyse ne me convainc pas du tout (ce qui ne veut pas dire que ton hypothese est fausse).

+0 -0

Tu as peut-être mal compris alors.

C’est évident que les meilleurs sont meilleurs (meilleurs pilote, voiture, mécaniciens et que sais-je). La partie intéressante des graphiques est l’étalement de la diagonale. Il traduit la manière dont on conserve sa place.

On voit que sur la tête de course, Monaco est plus déterminé à la qualif que la Chine. Une des raisons est qu’il est plus dur de doubler à Monaco qu’en Chine. Sachant que les pilotes et écuries de tête sont presque les mêmes sur toutes ces années !

La course en elle-même est assez différente de la qualif tant que les écarts entre voitures sont faibles. L’interférence entre voiture change le temps au tour et on peut doubler en étant un pilote un peu plus lent, mais plus habile. À condition qu’il y ait la place.

+2 -1

Je sais pas, est-ce que la difference de la distribution et donc de l’etalement est significatif entre ces deux circuits? Entre plusieurs circuits?

Tu dis 'oui okay, mais juste pour la tete de classement' ou justement c’est la que se situent les meilleurs et les plus reguliers. En plus, cela va totalement a l’encontre des graphiques qui montrent une plus grande difference au niveau des positions plus basses, en comparaison au top du classement.

+0 -0

Honnêtement, je n’ai pas la prétention de faire une analyse statistique complète. Si tu veux comparer tous les trucs possibles je te laisse faire.

On dirait aussi que tu fais exprès d’être de mauvaise foi. Tout à l’heure, tu disais que tout est expliqué facilement par une raison extérieure (la qualité des pilotes). Et là, tu oublies de penser aux causes extérieures de l’étalement de fond de classement…

La forme globale est commune aux deux courses que j’ai regardé, et on peut imaginer des causes communes très facilement (qu’on voit en vrai !) : irrégularité des pilotes, interférence massive dans le peloton, fiabilité douteuse des voitures en dehors du top, probabilité accrue d’accidents au contact…

Comme disait quelqu’un avant, on pourrait probablement mieux prédire le classement avec des paramètres plus fondamentaux : budget des écuries, puissance des groupes motopropulseurs, palmarès des pilotes…

+2 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte