Il y a quelques jours sur linuxfr.org, Julien Jorge a posté un journal intitulé « Exercices de programmation et benchmarks » dans lequel il fait divers tests de performances sur un exercice en C++, code à l’appui.
L’exercice est le suivant :
Étant donné une matrice d’entiers, l’exercice consiste à calculer la somme des nombres qui ne sont pas sous un zéro. Par exemple, pour
0, 2, 3 1, 0, 4 5, 6, 7Le résultat attendu est 2 + 3 + 4 + 7 = 16. Le 1, le 5 et le 6 ne sont pas comptés car il y a un zéro plus haut dans la colonne.
La matrice est représentée en row-major, c’est-à-dire par une table de tables où chaque sous table représente une ligne de la matrice.
C’est alors que je me suis fait les réflexions suivantes :
- Quelle seraient les performances des mêmes algorithmes, appliqués en Java et en Kotlin ?
- Y a-t-il une différence de performance entre Java et Kotlin ?
- Est-ce que les optimisations utilisées en C++ sont aussi efficaces en Java et Kotlin ?
- N’est-ce pas l’occasion de tester le framework de microbenchmark de Java ?
Et donc, je me suis mis à l’ouvrage.
Dans toute la suite du billet, je pars du principe que vous avez lu le journal d’origine !
- Le Java Microbenchmark Harness (JMH) avec Gradle et IntelliJ
- Des algorithmes par paquets de douze
- Des données de test
- Des résultats !
- Une analyse des résultats : 3 algos, 3 comportements différents
- Une digression sur le Java Microbenchmark Harness (JMH)
Le Java Microbenchmark Harness (JMH) avec Gradle et IntelliJ
La JVM, ça apporte des comportements complexes, donc pour faire des benchmark sérieux, il faut l’outillage adapté.
Ici l’outil, c’est le Java Microbenchmark Harness (JMH), qui premet de « chauffer » la JVM et de lancer chaque test plusieurs fois, pour avoir des statistiques plus fiables et plus précises.
Ce qui n’empêche pas qu’il faut savoir interpréter les résultats, d’ailleurs l’outil le précise systématiquement à la fin des tests :
REMEMBER: The numbers below are just data. To gain reusable insights, you need to follow up on why the numbers are the way they are. Use profilers (see -prof, -lprof), design factorial experiments, perform baseline and negative tests that provide experimental control, make sure the benchmarking environment is safe on JVM/OS/HW level, ask for reviews from the domain experts. Do not assume the numbers tell you what you want them to tell.
La configuration du JMH avec Gradle est facile. Si on fait les choses bien, on se retrouve avec une nouvelle racine de sources (src/jmh en plus de src/java et src/kotlin) dans lesquelles on peut mettre nos tests sans polluer le code métier.
En plus, IntelliJ reconnait automatiquement les tests, on peut les lancer directement sans avoir à jouer avec la ligne de commande 
Par contre l’outil semble très fortement couplé à Java et à OpenJDK, je n’ai pas réussi à écrire de test en Kotlin (si tant est que ça ait un intérêt), et n’ai pas trouvé de moyen simple de les lancer sur une JVM tierce (typiquement celle d’IBM).
Des algorithmes par paquets de douze
Le choix des algorithmes
L’auteur d’origine a testé des tas d’algoritmes, et je n’allais pas m’amuser à tous les tester, parce que ça aurait été :
- Impossible pour certains qui utilisent des spécificités du langage1
- Beaucoup trop long à coder.
- Beaucoup trop long à tester (je reviendrai là-dessus dans la partie sur les chiffres).
- Sans grand intérêt.
J’ai sélectionné trois algorithmes :
- L’implémentation la plus efficace, donc de référence, en C++ sur CodeSignal dite « BestRatings »
- La première implémentation à faire mieux en C++ que l’implémentation de référence, dite « Branches »,
- Et l’implémentation la plus efficace pour les grosses matrices, dite « Indices ».
À noter que tous ces algorithmes travaillent sur des const std::vector<std::vector<int>>& matrix dont je ne sais pas s’ils sont plus proches d’une List<List<Integer>> matrix ou d’un int[][] matrix en Java, donc dans le doute j’ai fait les deux variantes à chaque fois. Et chaque algo est testé en version Kotlin et en version Java.
Ça fait donc 3 algos x 2 formats de données x 2 langages = 12 méthodes à tester…
Les codes présentés ci-dessous sont disponibles dans leur contexte sur Github : dans ce dépôt pour les codes JVM, et ici pour les codes C++. Ce qui devrait vous permettre de les lancer vous-même si vous connaissez les langages en question.
L’algorithme BestRatings
En version C++ :
int matrix_elements_sum_best_ratings(const std::vector<std::vector<int>>& m)
{
int r(0);
for (int j=0; j<(int)m[0].size(); j++)
for (int i=0; i<(int)m.size(); i++)
{
if (m[i][j]==0)
break;
r += m[i][j];
}
return r;
}
L’algorithme est simplissime et direct, et pourtant très efficace.
Versions Java :
public static int sum(List<List<Integer>> matrix) {
int result = 0;
for (int j = 0; j < matrix.get(0).size(); j++) {
for (int i = 0; i < matrix.size(); i++) {
if (matrix.get(i).get(j) == 0) {
break;
}
result += matrix.get(i).get(j);
}
}
return result;
}
public static int sumArray(int[][] matrix) {
int result = 0;
for (int j = 0; j < matrix[0].length; j++) {
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][j] == 0) {
break;
}
result += matrix[i][j];
}
}
return result;
}
On peut remplacer la boucle interne for (int i = 0… par un « for étendu » for (List<Integer> integers : matrix) { sans que ça ne change quoi que ce soit au niveau des performances.
Versions Kotlin :
@JvmStatic
fun sum(matrix: List<List<Int>>): Int {
var result = 0
for (j in matrix[0].indices) {
for (i in matrix.indices) {
if (matrix[i][j] == 0) {
break
}
result += matrix[i][j]
}
}
return result
}
@JvmStatic
fun sumArray(matrix: Array<IntArray>): Int {
var result = 0
for (j in matrix[0].indices) {
for (i in matrix.indices) {
if (matrix[i][j] == 0) {
break
}
result += matrix[i][j]
}
}
return result
}
On remarque que le code est strictement identique à l’exception de la signature de la méthode… et hélas impossible à factoriser, puisqu’il manque un dénominateur commun aux types List et Array en Kotlin 
L’algorithme Branches
On maintient une liste des colonnes à ignorer pour éviter des tests si on a connaissance d’un 0 plus haut dans la colonne.
En version C++ :
int matrix_elements_sum_branches(const std::vector<std::vector<int>>& matrix)
{
const int row_size(matrix[0].size());
std::vector<char> usable_column(row_size, 1);
int result(0);
for (const std::vector<int>& row : matrix)
for (int i(0); i != row_size; ++i)
if (usable_column[i])
{
const int v(row[i]);
if (v == 0)
usable_column[i] = 0;
else
result += v;
}
return result;
}
En Java :
public static int sum(List<List<Integer>> matrix) {
boolean[] usableColumns = new boolean[matrix.size()];
Arrays.fill(usableColumns, true);
int result = 0;
for (List<Integer> row : matrix) {
for (int i = 0; i != row.size(); i++) {
if (usableColumns[i]) {
int v = row.get(i);
if (v == 0) {
usableColumns[i] = false;
} else {
result += v;
}
}
}
}
return result;
}
public static int sumArray(int[][] matrix) {
boolean[] usableColumns = new boolean[matrix.length];
Arrays.fill(usableColumns, true);
int result = 0;
for (int[] row : matrix) {
for (int i = 0; i != row.length; i++) {
if (usableColumns[i]) {
int v = row[i];
if (v == 0) {
usableColumns[i] = false;
} else {
result += v;
}
}
}
}
return result;
}
Et en Kotlin :
@JvmStatic
fun sum(matrix: List<List<Int>>): Int {
val usableColumns = BooleanArray(matrix.size)
Arrays.fill(usableColumns, true)
var result = 0
for (row in matrix) {
for (i in row.indices) {
if (usableColumns[i]) {
val v = row[i]
if (v == 0) {
usableColumns[i] = false
} else {
result += v
}
}
}
}
return result
}
@JvmStatic
fun sumArray(matrix: Array<IntArray>): Int {
// [...] (code identique à la méthode précédente, mais non factorisable)
}
L’algorithme Indices
L’inconvénient de l’algorithme précédent est qu’il nous oblige à parcourir les double boucles même quand on sait que lire certaines colonnes sont inutiles. On remplace donc notre référentiel de colonnes à tester par une liste de colonnes à tester, de façon à n’itérer que sur celles où c’est nécessaire.
En C++
int matrix_elements_sum_indices(const std::vector<std::vector<int>>& matrix)
{
const int row_size(matrix[0].size());
std::vector<int> usable_columns(row_size);
const auto usable_columns_begin(usable_columns.begin());
auto usable_columns_end(usable_columns.end());
std::iota(usable_columns_begin, usable_columns_end, 0);
int result(0);
for (const std::vector<int>& row : matrix)
for (auto it(usable_columns_begin); it != usable_columns_end;)
{
const int i(*it);
const int v(row[i]);
if (v == 0)
{
--usable_columns_end;
*it = *usable_columns_end;
}
else
{
result += v;
++it;
}
}
return result;
}
En Java
public static int sum(List<List<Integer>> matrix) {
List<Integer> usableColumns = IntStream.range(0, matrix.size()).boxed().collect(Collectors.toList());
int result = 0;
for (List<Integer> row : matrix) {
for (int it = 0; it < usableColumns.size(); it++) {
int i = usableColumns.get(it);
int v = row.get(i);
if (v == 0) {
usableColumns.remove(it);
it--;
} else {
result += v;
}
}
}
return result;
}
public static int sumArray(int[][] matrix) {
int[] usableColumns = IntStream.range(0, matrix.length).toArray();
int result = 0;
for (int[] row : matrix) {
for (int it = 0; it < usableColumns.length; it++) {
int i = usableColumns[it];
int v = row[i];
if (v == 0) {
usableColumns = ArrayUtils.remove(usableColumns, it);
it--;
} else {
result += v;
}
}
}
return result;
}
En Kotlin
@JvmStatic
fun sum(matrix: List<List<Int>>): Int {
val usableColumns =
IntStream.range(0, matrix.size).boxed().collect(Collectors.toList())
var result = 0
for (row in matrix) {
var it = 0
while (it < usableColumns.size) {
val i = usableColumns[it]
val v = row[i]
if (v == 0) {
usableColumns.removeAt(it)
it--
} else {
result += v
}
it++
}
}
return result
}
@JvmStatic
fun sumArray(matrix: Array<IntArray>): Int {
var usableColumns = IntStream.range(0, matrix.size).toArray()
var result = 0
for (row in matrix) {
var it = 0
while (it < usableColumns.size) {
val i = usableColumns[it]
val v = row[i]
if (v == 0) {
usableColumns = ArrayUtils.remove(usableColumns, it)
it--
} else {
result += v
}
it++
}
}
return result
}
C’est l’algorithme dont l’écriture en Kotlin s’écarte le plus de la version Java.
-
Par exemple le tout premier présenté contient une interprétation d’une inégalité comme un entier :
↩usable_column[i] *= (v != 0), ce qui n’est pas possible en Java sans casser le concept voulu par l’auteur.
Des données de test
Pour que les tests soient compables, il me fallaient des données qui ressemblent au jeu de test d’origine. Or l’auteur ne travaille pas avec des données fixes, mais génère des matrices aléatoires, où la proportion d’avoir des 0 augmente avec la profondeur dans la matrice. Évidemment, les temps de génération de la matrice ne sont pas comptabilités dans les tests de performance. J’ai donc copié son algorithme :
std::vector<std::vector<int>> random_matrix(int s)
{
static std::unordered_map<int, std::vector<std::vector<int>>> cache;
boost::random::mt19937 gen(g_seed);
boost::random::uniform_int_distribution<int> rg;
const int row_size(s);
const int row_count(s);
const int max_value(100);
std::vector<std::vector<int>> matrix(row_count);
for (int y(0); y != row_count; ++y)
{
std::vector<int>& row(matrix[y]);
row.resize(row_size);
for (int x(0); x != row_size; ++x)
if (rg(gen) % s >= y)
row[x] = 1 + rg(gen) % (max_value - 1);
else
row[x] = 0;
}
return matrix;
}
Qui devient :
List<List<Integer>> randomMatrix(int size) {
Random rg = seed == null ? new Random() : new Random(seed);
final int maxValue = 100;
List<List<Integer>> matrix = new ArrayList<>(size);
for (int y = 0; y != size; y++) {
List<Integer> row = new ArrayList<>(size);
for (int x = 0; x != size; x++) {
row.add(x, rg.nextInt(size) >= y ? (1 + rg.nextInt(maxValue - 1)) : 0);
}
matrix.add(y, row);
}
cache.put(size, matrix);
return matrix;
}
Manipuler les nombres aléatoires me semble bien plus confortable en Java.
Des résultats !
Matériel de test
Je ne sais pas lancer le code C++ directement sur ma machine. Les résultats C++ ont donc directement été récupérés sur le journal d’origine !
Matériel de test pour le C++ :
Run on (4 X 3100 MHz CPU s)
CPU Caches:
L1 Data 32 KiB (x2)
L1 Instruction 32 KiB (x2)
L2 Unified 256 KiB (x2)
L3 Unified 3072 KiB (x1)
Matériel de test JVM (Java / Kotlin) :
Run on AMD Ryzen 5 3600X 6-Core Processor (12 X 3800 MHz CPU s)
CPU Caches:
L1 Data 32 KiB (x6)
L1 Instruction 32 KiB (x6)
L2 Unified 512 KiB (x6)
L3 Unified 16 MiB (x2)
Un petit tableau ?
Temps d’exécution moyen, en nanosecondes, en fonction de l’algorithme et de la taille de la matrice :
| Taille | 10 x 10 | 100 x 100 | 1000 x 1000 | 10000 x 10000 |
|---|---|---|---|---|
| branches C++ | 116 | 7 689 | 481 443 | 70 364 814 |
| bestRatings C++ | 42 | 1 091 | 41 886 | 3 454 125 |
| bestRatings | 54 | 1 802 | 70 637 | 2 991 120 |
| bestRatingsKt | 101 | 2 456 | 83 027 | 3 393 295 |
| bestRatingsArray | 31 | 717 | 29 160 | 1 265 142 |
| bestRatingsArrayKt | 30 | 784 | 26 995 | 1 448 296 |
| branches | 117 | 5 003 | 550 489 | 27 319 417 |
| branchesKt | 110 | 4 658 | 639 811 | 41 354 458 |
| branchesArray | 80 | 4 465 | 426 882 | 27 351 947 |
| branchesArrayKt | 73 | 4 803 | 444 350 | 38 913 710 |
| indices | 380 | 7 188 | 206 245 | 6 069 782 |
| indicesKt | 363 | 6 986 | 170 402 | 5 786 547 |
| indicesArray | 203 | 3 528 | 220 594 | 18 778 910 |
| indicesArrayKt | 204 | 3 620 | 234 809 | 18 853 039 |
Je n’ai hélas pas le chiffre pour l’algorithme indices en C++, l’auteur ne donne pas les valeurs avec les tailles en puissance de 10 pour cet algorithme.
Bon, on est d’accord, on ne voit pas grand-chose. On remarque néanmoins que :
- Les ordres de grandeur entre les résultats C++ et JVM (Java, Kotlin) sont les mêmes.
- Les versions Kotlin et Java ont des résultats identiques (à la variabilité des tests près).
On va essayer de rendre ça un peu plus clair…
Un graphique pour les étudier tous
Je relance donc mes benchmark, cette fois sur toutes les tailles de matrice qui sont des puissances entières de 2 entre 214 (soit 16 384)1. J’enlève les versions Kotlin, vu que les résultats sont identiques aux versions Java, pour garder un graphique lisible. Je récupère aussi les valeurs des mêmes algorithmes en C++ sur les mêmes tailles de matrice depuis le dépôt Git d’origine.
Ensuite, je fais la même chose que sur le journal d’origine : je normalise toutes les valeurs en prenant l’implémentation C++ « bestRatings » en référence, donc avec un temps d’exécution relatif qui vaut 1 pour toutes les tailles de matrices.
Et donc, on obtinent ce graphique, avec 3 couleurs pour les 3 types d’algorithmes.
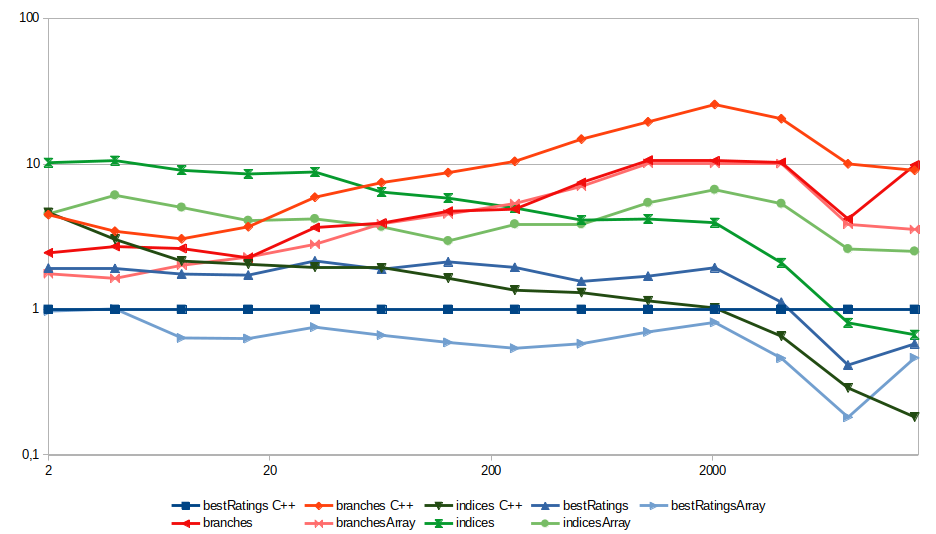
Ce qu’on observe est si intéressant que je vais écrire une section complète dessus !
-
Ce qui donne des grosses matrices pour les dernières tailles : une matrice d’entiers (
↩intde 4 octets) de 16 384 * 16 384 prends exactement 1 Go de RAM pour les données seules !
Une analyse des résultats : 3 algos, 3 comportements différents
L’algorithme BestRatings (en bleu)
Tant qu’on est pas sur des matrices proprement gigantesques, la version JVM avec listes est légèrement plus lente et la version JVM avec tableaux est légèrement plus rapide que la version C++.
Dans tous les cas on est dans les mêmes ordres de grandeur (facteur environ 2–3 entre les versions les plus lentes et les plus rapides de l’algorithme).
L’algorithme Branches
Cet algorithme offre un résultat très curieux : les performances des deux implémentations JVM (listes et tableaux) sont pratiquement identiques… et systématiquement plus rapides que la version C++. On peut supposer que le compilateur JIT (Just-In-Time) de la JVM arrive particulièrement bien à optimiser ce code, par rapport à la version C++ native. On reste néanmoins dans les mêmes ordres de grandeur (facteur environ 2–3 entre les versions JVM et C++ de l’algorithme).
Ça serait intéressant si l’algorithme n’était pas aussi le plus lent dès que les matrices sont un peu grosses…
L’algorithme Indices
Ici, au contraire, les versions JVM sont systématiquement plus lentes que la version C++. Mais au contraire des deux autres où les versions à base de listes et de tableau avaient des comportements proches, ici les deux versions JVM ont des comportements différents au fur et à mesure que la taille des matrices grossit. C’est au point que la version JVM avec listes, qui est pour toutes les petites tailles l’algorithme le plus lent de tous, arrive à battre le BestRating C++ sur les très grosses matrice !
Les algorithmes entre eux
Contrairement au C++ où Indices battait BestRatings pour les très grosses matrices, aucun algorithme ne fait mieux que BestRatings en restant sur la JVM.
En première approche, ceci s’explique sans doute parce que le surcout des structures de contrôles est relativement élevé et n’est pas compensé par le gain en performances, contrairement au C++ qui permet de travailler au plus près du processeur.
On voit néanmoins que la JVM, grâce à son compilateur JIT, a des performances tout à fait honorables qui n’ont pas grand-chose à envier à du code natif en terme de puissance de calcul pure.
Enfin, une différence à priori mineure (un code implémenté avec des tableaux et non des ArrayList – qui stockent pourtant leurs données dans un tableau) peut apporter des différences de comportement significatives.
Une digression sur le Java Microbenchmark Harness (JMH)
Le Java Microbenchmark Harness (JMH) est très pratique, à commencer parce qu’il permet de faire des mesures de performances de fonction de manière stable et fiable. Ce qui en soit est compliqué avec une JVM, à cause de tous les mécanismes internes.
Le revers de la médaille, c’est que c’est long.
Le comportement standard du JMH, c’est de faire des run de 10 secondes pendant lesquelles il lance en boucle la fonction à tester.
Pour être sûr que le compilateur JIT est bien lancé, la fréquence processeur stabilisée et tous les caches en place, il commence par faire 5 run « à blanc », sans tenir compte des résultats.
Puis, pour avoir un résultat fiable, il refait 5 run, cette fois en collectant les mesures.
Ça veut dire 50 secondes d’exécution pure par méthode à tester, plus la collecte etc. Donc générer les 14 valeurs pour chacun des 6 algorithmes pour JVM du graphique ci-dessus, ça m’a pris plus d’une heure. Évidemment, comme c’est un test de performances, on ne lance pas les tests en parallèle sur plusieurs threads, ça irait plus vite mais fausserait complètement les résultats…
D’accord, le titre était un peu provocateur… cela dit, j’aurais pu soigneusement choisir mes résultats (l’algorithme Branches et l’implémentation en tableaux de l’algorithme BestRatings) pour clamer haut et fort que Java et Kotlin sont plus rapides que C++.
Ce qui aurait été mensonger et pas très intéressant, d’autant que ce petit test a mis en exergue des comportements curieux et notables. Voici ce que je dirais en conclusion :
- La JVM a de bonnes performances de calcul. On ne peut claiment plus dire que « Java c’est lent » sans passer pour un ignare qui méconnait son sujet. Évidemment, si votre besoin (et j’insiste, « besoin » et non « envie ») c’est la perfomance maximale, un langage plus proche de la machine est souhaitable ; si vous avez simplement besoin que ce soit raisonnablement performant, la JVM est là pour vous.
- Un algorithme n’est pas bon dans l’absolu. On l’a vu : le meilleur algorithme en C++ n’est pas le meilleur algorithme sur JVM. Testez et vérifiez, toujours !
- Le meilleur algorithme dépend de vos données. Quel que soit le langage, le meilleur algorithme pour traiter de petites matrices n’est pas le meilleur pour traiter de grosses matrices. Là encore, testez et vérifiez.
Et dans tous les cas, si vous avez réellement besoin de performances sur une section critique de votre programme, ne vous contentez pas simplement d’un bête microbenchmark ou d’un benchmark tout court ; comme le dit la sortie du JMH :
REMEMBER: The numbers below are just data. To gain reusable insights, you need to follow up on why the numbers are the way they are. Use profilers (see -prof, -lprof), design factorial experiments, perform baseline and negative tests that provide experimental control, make sure the benchmarking environment is safe on JVM/OS/HW level, ask for reviews from the domain experts. Do not assume the numbers tell you what you want them to tell.




