L’histoire de la constante 0x5f3759df (et de la fonction Q_rsqrt) est relativement célèbre, mais pour l’intérêt pédagogique qu’elle représente, je me permets de vous la raconter à nouveau. Pour la faire courte, il s’agit d’une fonction qu’on retrouve entre autres dans le code source de Quake III (qui en est probablement la plus célèbre itération), même si sont histoire est probablement plus ancienne que ça.
Si vous ne la connaissez pas encore, restez par ici, c’est sympa: même si ce n’est plus rentable aujourd’hui, on va un peu explorer ce qui a derrière, et jouer avec le compilateur (et des GPUs !) pour bien comprendre tout ça !
Ce billet requiert, pour être compris, d’avoir vu la notion de logarithme, et d’avoir une vague idée de comment fonctionne l’assembleur. Sur cette deuxième partie, je ne garanti pas l’exactitude de toutes les informations, donc n’hésitez pas à me corriger en commentaire
Comment?
Le code de cette célèbre fonction, telle qu’on la retrouve dans le code source de Quake III, est le suivant (avec les commentaires originaux, mais sans le isnan, qui est la version qu’on voit généralement sur internet):
float Q_rsqrt( float number )
{
long i; /* NOTE: il vaut mieux utiliser des `int32_t` aujourd'hui (voir ci-dessous) */
float x2, y
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
Bien que ça ne soit pas évident pour le moment, ce code permet de calculer comme une bonne approximation de la fonction inverse d’une racine carrée, , ou (même chose écrit autrement).
Il s’agit d’une opération qu’on retrouve assez couramment dans un moteur 3D. En effet, celui-ci utilise des vecteurs normés, c’est à dire qu’on divise ceux-ci par leur "taille". Autrement dit, à partir d’un vecteur , le vecteur est obtenu via
où on voit très clairement apparaître l’inverse de la racine carrée d’un nombre, en l’occurrence le carré de la norme du vecteur, .
L’astuce qui est utilisée ici tient en deux étapes. La première concerne les lignes 8 à 11, et consiste à exploiter la représentation IEEE 754. La seconde étape consiste en la ligne 12 (et 13, mais elle a été commentée), et est une amélioration de la valeur obtenue dans la première étape.
À l’époque ou ce code était utilisé (milieux des années 90), les processeurs étaient évidemment plus lents qu’aujourd’hui, et en plus de ça, le matériel dédié à la 3D était encore balbutiant (la première carte graphique célèbre intégrant de telles fonctions est la Voodoo de 3dfx sort fin 96). Pour ajouter à l’intérêt de cette fonction, travailler avec des nombres flottant était à l’époque beaucoup plus lent que de travailler sur des entiers, et la division était particulièrement inefficace (notez que ce code n’en contient pas). Tout ceci fait qu’à l’époque, une telle astuce permettait d’accélérer nettement le calcul pour une perte de précision mineure (<1%).
Première étape: evil floating point bit level hacking, puis what the fuck?
"I triple E sept-cent-cinquante-quatre" !
Comme expliqué par @Aabu dans son tutoriel, la représentation des nombres réel en binaire suis (généralement) le standard IEEE 754.1 Celui-ci est stocké dans une unique série de bits en 3 parties distinctes (pour un nombre normalisé):
- , le bit de signe, qui vaut zéro (positif) ou 1 (négatif). Par la suite, je vais me permettre de noter , où est la taille de , qui vaut ici un bit.
- , l’exposant. En fait, est stocké sous la forme d’un nombre entre 0 et (valeur maximale qu’on peut stocker dans un nombre contenant bits) et l’exposant utilisé en pratique dans le réel est calculé comme , où est le biais, pour obtenir un exposant compris entre et .
- , la mantisse, avec . Encore une fois, en pratique, est stocké sous la forme d’un nombre compris entre et , tandis que dans la représentation IEEE 754, il est divisé par pour donner un nombre entre 0 et 1.
On peut écrire le réel selon le standard IEEE 754 comme , où , et sont les valeurs numériques des 3 parties du nombre flottant. On en connaît la valeur, vu ce qu’on a dit plus haut, grâce à la formule suivante:
On peut également (ça nous servira pour la suite) calculer la valeur qu’aurait ce nombre si ces bits étaient interprétés comme un entier avec
float ?
Ici, on utilise plus particulièrement le float, soit, en C, un nombre à virgule défini sur 32 bits. Les 3 parties sont arrangées comme suit:

On a donc , et dès lors et . On peut également vérifier que notre formule fonctionne sur l’exemple donné ci-dessus, puisque (notez l’indice 2, qui indique qu’il s’agit de binaire), donc
ce qui fait bien 0,15625. Par ailleurs, on peut calculer que , ce qui est bien le résultat du calcul suivant:
C’est bien gentil, tout ça, mais ou est l’astuce ?
Avant d’expliquer le détail du code, commençons par faire un pas de côté. Il est un temps pas si lointain ou la calculatrice était hors de prix ou n’existait pas. Nos ancêtres (même si certains vivent encore aujourd’hui) utilisaient alors des tables de logarithmes (ou des règles à calcul, selon la précision demandée). Trois propriétés sont alors intéressantes à exploiter:
- : autrement dit, pour calculer la multiplication de deux nombres, il suffit d’additionner la valeur de leurs logarithmes, puis d’utiliser une table de logarithme inverse, autrement dit, si on utilise le logarithme en base 10, calculer , avec . Seule limitation, et doivent être positif (il n’existe pas de logarithme d’un nombre négatif). Notez également que ça fonctionne pour n’importe quelle base de logarithme, même si les plus courantes sont la base 10 et la base .
- : autrement dit, pour calculer la puissance (qui peut très bien être réel et/ou négatif) d’un nombre (lui strictement positif), on multiplie la valeur de son logarithme par , puis on utilise encore une fois une table de logarithme inverse.
- Des deux propriétés précédentes, on peut déduire .
Autrement dit, plutôt que de calculer , on pourrait calculer (j’ai utilisé la seconde propriété),
Notez que vu qu’on est dans le contexte de l’informatique, on utilise des logarithmes en base 2, puisqu’on manipule des bits.
Bon, ça parait pas très malin, puisque le logarithme semble être une opération à priori aussi complexe qu’une racine carrée Sauf que et sont tout deux des nombres réels dont on part du principe qu’il s’agit de deux
float représentés selon la norme IEEE 754.
Dès lors, vu que et ,
Bien entendu, on ne peut calculer la racine carré que d’un nombre positif, donc on peut partir du principe que , ce qui simplifie:
En utilisant la première propriété, on peut séparer le produit en une somme de logarithmes, et
À ce niveau, il semblerait qu’on soit coincé. En effet, il n’existe pas de simplification exacte pour le logarithme d’une somme. Par contre, on peut approximer ce logarithme en utilisant une série de Taylor. On va choisir la forme suivante:
où est une constante, dont la valeur peut être choisie. En effet, puisque , est compris entre 0 et 1. On va donc choisir cette constante afin de minimiser la valeur du logarithme et notre approximation sur cet intervalle:
On peut montrer que la valeur qui fonctionne bien pour ça est , mais comme on le verra, il ne s’agit que d’un détail. Graphiquement, on obtient ceci
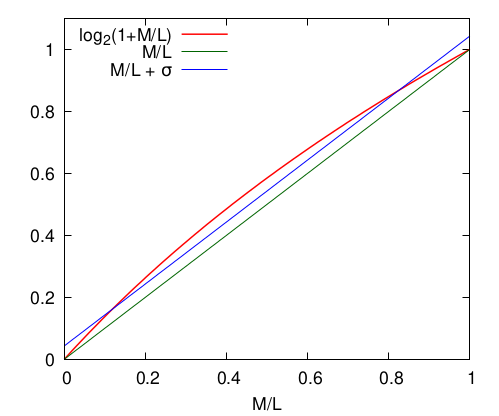
Autrement dit, le choix de permet de passer d’une approximation (courbe verte, ) exacte à et , mais moins bonne aux alentours de à une approximation ( idéal) qui donne, globalement, des résultats plus proches de la réalité.
On peut donc maintenant écrire
Et là, on a réussi à faire apparaître les représentations entières de et (avec le bit de signe à 0) ! Dès lors, on peut finalement simplifier et obtenir
Et ce calcul, c’est littéralement la ligne 10 du code de la fonction Q_rsqrt (n’oubliez pas que décaler les bits vers la droite d’un entier le divise par 2, 4 >> 1 est égal à 2). C’est beau, non ? Quant au evil floating point bit level hacking, il s’agit de la manière d’obtenir la représentation entière d’un nombre flottant. En effet, i = (long) y n’aurait pas fonctionné (C aurait uniquement renvoyé la partie entière de y, alors qu’on veut lui faire croire qu’il s’agit d’un entier). Il faut donc forcer la main à C, ce qui en développé donne ceci
/* Ce code est équivalent à la ligne 9 du code ci-dessus: */
long* tmp = NULL; // on crée un pointeur vers un `long`
tmp = (long*) &y; // on le fait pointer vers `y` (en faisant un cast)
i = *tmp; // on donne à `i` la valeur de `tmp`
Si les pointeurs sont un peu loin pour vous, je vous invite à relire le chapitre correspondant de l’excellent tutoriel C de ZdS. Notez ceci dit que, bien que ça fonctionne, ce n’est pas une utilisation courante des pointeurs
On fait bien entendu la manipulation inverse à la ligne 11 pour obtenir la représentation flottante de y, qui est notre réponse.
Cette astuce fonctionne encore aujourd’hui, comme on le verra plus bas.
En principe, le code était compilé et exécuté dans l’environnement le plus courant à l’époque : les processeurs 32 bits. Dès lors, la taille d’un long était de 4 octets (la même que la taille d’un float). Aujourd’hui, sur un processeur 64 bits, la taille est de 8 octets, ce qui peut poser des problèmes. On peut donc utiliser un int32_t pour régler ça, et c’est ce que je ferais dans la seconde section.
Par ailleurs, comme le fait très justement remarquer Wikipédia, il s’agit normalement d’un undefined behavior: le compilateur a le droit d’interpréter la ligne 9 de Q_rsqrt (ou la ligne 3 du code ci-dessus) comme bon lui semble. On peut éviter ce problème en utilisant une union (en C) ou std::bit_cast<std::uint32_t>() (en C++).
Pour en terminer avec cette partie du code, on a donc que , une fois réinterprété comme un entier, vaut à peu près 0x5f3759df (1 597 463 007 en base 10), d’où notre constante magique. Je dis "à peu près", car la valeur est normalement 1 597 488 309,5740416 (qu’on peut calculer vu qu’on connaît les valeurs de et pour nos flottants 32 bits), soit, si on en garde la valeur entière, 0x5f37bcb5. En fait, la constante a très probablement été ajustée pour donner une meilleure précision après la deuxième étape
Second étape: 1st iteration
On verra ci-dessous que l’approximation qu’on a obtenue tient la route, mais on peut encore l’améliorer sans faire trop de calculs supplémentaires grâce à la méthode de Newton. Cette méthode est en fait utilisée pour trouver numériquement les zéros d’une fonction [les solutions de l’équation ] par itérations successives. Pour ce faire, on approxime que la fonction est linéaire, et que l’intersection de cette droite avec l’axe des x correspond à une bonne approximation du zéro. Puis on itère.

Il s’agit donc d’un algorithme itératif, dont le point suivant est obtenu grâce à
où est la dérivée de . Pour plus de détails mathématiques, je vous renvoie à ce tutoriel de @Holosmos.
Du coup, on va choisir une fonction telle que son zéro soit la valeur recherchée. Prenons
Grâce à cette formulation, si est égal à 0, alors cela signifie que est exactement l’inverse de la racine carrée de . La formule itérative devient alors
ce qui correspond bien à la ligne 12 (et 13) du code de Q_rsqrt. On voit que les auteurs se sont limités à une itération de la méthode de Newton, probablement pour des raisons de coup/performance. Le tour est joué
Généralisation
Évidement, c’est généralisable à tout calcul du type pour tout différent de zéro. En résumé, on obtient, pour la première étape
et pour la seconde,
sauf que vu que le but était d’éviter les divisions, ça n’est intéressant que pour (qui évite la division par ). On remarque également que la constante magique est toujours un multiple de , c’est à dire pour un float environ 1 064 992 206, soit 0x3f7a7dce (encore une fois, on peut ensuite l’ajuster).
- Et à ce sujet, n’oubliez pas de lire What Every Computer Scientist Should Know About Floating-Point Arithmetic, http://perso.ens-lyon.fr/jean-michel.muller/goldberg.pdf↩
Et ça marche ?
TL;DR: oui, mais ce n’est plus rentable.
Précision
Premièrement, intéressons-nous à la précision, pour voir si ça vaut (valait?) le coup:
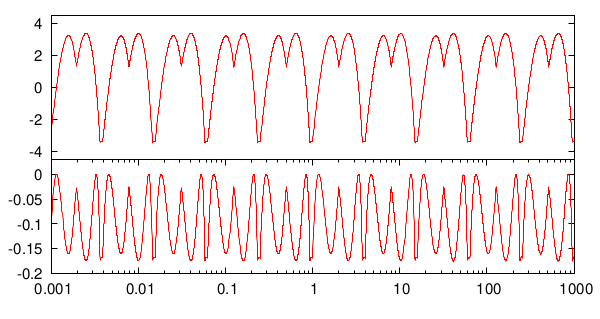
Deux choses sont très clairement visibles:
- si on se restreint à la première étape, l’erreur relative évolue périodiquement1 entre environ -3 et 3%, et
- si on ajoute une itération de l’algorithme de Newton, on améliore l’erreur relative d’un facteur, puisqu’elle est cette fois comprise entre 0 et -0,2%. 2
Ça peut paraître encore beaucoup3, mais c’est amplement suffisant pour l’époque En effet, les moteurs de rendus 3D privilégiait (et c’est encore le cas) la quantité à la qualité.4 Les données y sont d’ailleurs encore représentés sous la forme de
float au lieu de double.
Performances
Jouons avec le compilateur
Pour tester les performances, j’ai écrit un second code qui mesure les performances respectives de rsqrt et Q_rsqrt sur un même tableau de 1 000 000 de float aléatoires, à l’aide d’une boucle for. Le code n’est en soi pas très compliqué si vous connaissez le C, à part peut être le code de la fonction rsqrt:
float rsqrt(float number) {
float res;
#ifdef USE_rsqrtss
asm ("rsqrtss %1, %0" : "=x" (res) : "xm" (number));
#else
res = 1.f / sqrtf(number);
#endif
return res;
}
En effet, je vais comparer deux versions: celle, purement en C, où on calcule l’inverse de la racine carrée et celle, en assembleur, où on utilise l’instruction rsqrtss, qui est l’instruction processeur (en x86_64) pour calculer l’inverse d’une racine carrée.
Ce test n’est pas uniquement un test de performance. En effet, il y a également une pénalité d’accès la mémoire qui entache la performance des deux approches (mais qui devrait être similaire pour les deux fonctions).
Je vais effectuer ces tests sur mon AMD Ryzen 5 1500x (ordinateur personnel, acheté en 20185). Le programme est lancé 1000 fois et une moyenne est ensuite calculée:
| Commande | Q_rsqrt |
rsqrt() |
rsqrt() avec -DUSE_rsqrtss |
|---|---|---|---|
gcc -lm -o test perf.c -O0 && ./test |
8.08 ns/float | 5.69 ns/float | 4.22 ns/float |
gcc -lm -o test perf.c -O3 && ./test |
1.40 ns/float | 3.28 ns/float | 2.42 ns/float |
gcc -lm -o test perf.c -Ofast && ./test |
1.44 ns/float | 1.35 ns/float | 2.40 ns/float |
gcc -lm -o test perf.c -Ofast -mavx && ./test |
1.38 ns/float | 1.38 ns/float | 2.41 ns/float |
gcc.On peut constater deux choses: rsqrt() est effectivement plus rapide, particulièrement si on empêche gcc d’optimiser le code avec -O0. Dans ce cas là, il est même plus intéréssant d’utiliser directement la fonction en assembleur. Par contre, Q_rsqrt devient étrangement plus intéressant avec -O3, puis rsqrt (sans assembleur) devient compétitif -Ofast (-O3 et -ffast-math). Pour bien comprendre ce qui se passe, on peut s’amuser à regarder le code assembleur du programme avec objdump.
Pour Q_rsqrt avec -O0, gcc traduit bêtement le code source en assembleur, puis fait un call dans la boucle for de main.
$ gcc -g -lm -o test perf.c -O0 && objdump -dS -M intel ./test
(...)
float Q_rsqrt(float number)
{
401166: 55 push rbp
401167: 48 89 e5 mov rbp,rsp
40116a: f3 0f 11 45 ec movss DWORD PTR [rbp-0x14],xmm0
int32_t i;
float x2, y;
const float threehalfs = 1.5F;
40116f: f3 0f 10 05 f5 0e 00 movss xmm0,DWORD PTR [rip+0xef5] # 40206c <__dso_handle+0x64>
401176: 00
401177: f3 0f 11 45 fc movss DWORD PTR [rbp-0x4],xmm0
x2 = number * 0.5F;
40117c: f3 0f 10 4d ec movss xmm1,DWORD PTR [rbp-0x14]
401181: f3 0f 10 05 e7 0e 00 movss xmm0,DWORD PTR [rip+0xee7] # 402070 <__dso_handle+0x68>
401188: 00
401189: f3 0f 59 c1 mulss xmm0,xmm1
40118d: f3 0f 11 45 f8 movss DWORD PTR [rbp-0x8],xmm0
y = number;
401192: f3 0f 10 45 ec movss xmm0,DWORD PTR [rbp-0x14]
401197: f3 0f 11 45 f0 movss DWORD PTR [rbp-0x10],xmm0
i = * ( int32_t * ) &y;
40119c: 48 8d 45 f0 lea rax,[rbp-0x10]
4011a0: 8b 00 mov eax,DWORD PTR [rax]
4011a2: 89 45 f4 mov DWORD PTR [rbp-0xc],eax
i = 0x5f3759df - ( i >> 1 );
4011a5: 8b 45 f4 mov eax,DWORD PTR [rbp-0xc]
4011a8: d1 f8 sar eax,1
4011aa: 89 c2 mov edx,eax
4011ac: b8 df 59 37 5f mov eax,0x5f3759df
4011b1: 29 d0 sub eax,edx
4011b3: 89 45 f4 mov DWORD PTR [rbp-0xc],eax
y = * ( float * ) &i;
4011b6: 48 8d 45 f4 lea rax,[rbp-0xc]
4011ba: f3 0f 10 00 movss xmm0,DWORD PTR [rax]
4011be: f3 0f 11 45 f0 movss DWORD PTR [rbp-0x10],xmm0
y = y * ( threehalfs - ( x2 * y * y ) );
4011c3: f3 0f 10 45 f0 movss xmm0,DWORD PTR [rbp-0x10]
4011c8: 0f 28 c8 movaps xmm1,xmm0
4011cb: f3 0f 59 4d f8 mulss xmm1,DWORD PTR [rbp-0x8]
4011d0: f3 0f 10 45 f0 movss xmm0,DWORD PTR [rbp-0x10]
4011d5: 0f 28 d1 movaps xmm2,xmm1
4011d8: f3 0f 59 d0 mulss xmm2,xmm0
4011dc: f3 0f 10 45 fc movss xmm0,DWORD PTR [rbp-0x4]
4011e1: 0f 28 c8 movaps xmm1,xmm0
4011e4: f3 0f 5c ca subss xmm1,xmm2
4011e8: f3 0f 10 45 f0 movss xmm0,DWORD PTR [rbp-0x10]
4011ed: f3 0f 59 c1 mulss xmm0,xmm1
4011f1: f3 0f 11 45 f0 movss DWORD PTR [rbp-0x10],xmm0
return y;
4011f6: f3 0f 10 45 f0 movss xmm0,DWORD PTR [rbp-0x10]
}
(...)
results_rsqrt[i] = rsqrt(the_floats[i]);
401319: 8b 45 f8 mov eax,DWORD PTR [rbp-0x8]
40131c: 48 98 cdqe
40131e: 8b 84 85 60 e5 f9 ff mov eax,DWORD PTR [rbp+rax*4-0x61aa0]
401325: 66 0f 6e c0 movd xmm0,eax
401329: e8 df fe ff ff call 40120d <rsqrt>
40132e: 66 0f 7e c0 movd eax,xmm0
401332: 8b 55 f8 mov edx,DWORD PTR [rbp-0x8]
401335: 48 63 d2 movsxd rdx,edx
401338: 89 84 95 60 b0 ed ff mov DWORD PTR [rbp+rdx*4-0x124fa0],eax
Par contre, quand on lui permet d’optimiser (avec -O3 ou -Ofast), gcc se permet plusieurs choses:
- De simplifier un peu le code de la fonction, en retirant les constantes et les variables intermédiaires ;
- D’intégrer directement le code de ladite fonction dans la boucle
for, afin de supprimer l’appel, et d’avoir à perdre du temps à gérer la stack (pile) ; - Mais surtout, d’utiliser des instructions SSE!
$ gcc -g -lm -o test perf.c -Ofast && objdump -dS -M intel ./test
(...)
for(i=0; i < N_FLOAT; i++)
results_qrsqrt[i] = Q_rsqrt(the_floats[i]);
401100: 0f 28 44 04 10 movaps xmm0,XMMWORD PTR [rsp+rax*1+0x10]
i = 0x5f3759df - ( i >> 1 );
401105: 66 0f 6f d5 movdqa xmm2,xmm5
401109: 66 0f 6f c8 movdqa xmm1,xmm0
y = y * ( threehalfs - ( x2 * y * y ) );
40110d: 0f 59 c4 mulps xmm0,xmm4
i = 0x5f3759df - ( i >> 1 );
401110: 66 0f 72 e1 01 psrad xmm1,0x1
401115: 66 0f fa d1 psubd xmm2,xmm1
y = y * ( threehalfs - ( x2 * y * y ) );
401119: 0f 28 ca movaps xmm1,xmm2
40111c: 0f 59 ca mulps xmm1,xmm2
40111f: 0f 59 c1 mulps xmm0,xmm1
401122: 0f 28 cb movaps xmm1,xmm3
401125: 0f 5c c8 subps xmm1,xmm0
401128: 0f 59 ca mulps xmm1,xmm2
results_qrsqrt[i] = Q_rsqrt(the_floats[i]);
40112b: 0f 29 4c 05 00 movaps XMMWORD PTR [rbp+rax*1+0x0],xmm1
for(i=0; i < N_FLOAT; i++)
401130: 48 83 c0 10 add rax,0x10
401134: 48 3d 80 1a 06 00 cmp rax,0x61a80
40113a: 75 c4 jne 401100 <main+0x80>
C’est la même histoire pour rsqrt: avec -Ofast, gcc se permet de remplacer le code de la fonction par l’instruction rsqrtps, qui est la version SSE de rsqrtss. Il utilise par contre sqrtss (qui calcule la racine carrée, non son inverse) avec -O3.
$ gcc -g -lm -o test perf.c -O3 && objdump -dS -M intel ./test
(...)
for(i=0; i < N_FLOAT; i++)
40116a: 66 0f 1f 44 00 00 nop WORD PTR [rax+rax*1+0x0]
results_rsqrt[i] = rsqrt(the_floats[i]);
401170: f3 0f 10 44 1c 10 movss xmm0,DWORD PTR [rsp+rbx*1+0x10]
res = 1.f / sqrtf(number);
401176: 0f 2e c8 ucomiss xmm1,xmm0
401179: 0f 87 2c 01 00 00 ja 4012ab <main+0x21b>
40117f: f3 0f 51 c0 sqrtss xmm0,xmm0
401183: 0f 28 d3 movaps xmm2,xmm3
401186: f3 0f 5e d0 divss xmm2,xmm0
results_rsqrt[i] = rsqrt(the_floats[i]);
40118a: f3 0f 11 94 1c 10 35 movss DWORD PTR [rsp+rbx*1+0xc3510],xmm2
401191: 0c 00
for(i=0; i < N_FLOAT; i++)
401193: 48 83 c3 04 add rbx,0x4
401197: 48 81 fb 80 1a 06 00 cmp rbx,0x61a80
40119e: 75 d0 jne 401170 <main+0xe0>
$ gcc -g -lm -o test perf.c -Ofast && objdump -dS -M intel ./test
(...)
res = 1.f / sqrtf(number);
401160: 0f 28 74 04 10 movaps xmm6,XMMWORD PTR [rsp+rax*1+0x10]
401165: 0f 52 ce rsqrtps xmm1,xmm6
401168: 0f 28 c6 movaps xmm0,xmm6
40116b: 0f 29 34 24 movaps XMMWORD PTR [rsp],xmm6
40116f: 0f 59 c1 mulps xmm0,xmm1
401172: 0f 59 c1 mulps xmm0,xmm1
401175: 0f 59 ca mulps xmm1,xmm2
401178: 0f 58 c3 addps xmm0,xmm3
40117b: 0f 59 c1 mulps xmm0,xmm1
for(i=0; i < N_FLOAT; i++)
results_rsqrt[i] = rsqrt(the_floats[i]);
40117e: 0f 29 84 04 10 35 0c movaps XMMWORD PTR [rsp+rax*1+0xc3510],xmm0
401185: 00
for(i=0; i < N_FLOAT; i++)
401186: 48 83 c0 10 add rax,0x10
40118a: 48 3d 80 1a 06 00 cmp rax,0x61a80
401190: 75 ce jne 401160 <main+0xe0>
Bref, si on laisse gcc faire son travail, il peut optimiser un maximum l’exécution, ici pour arriver à environ 1 nanoseconde par nombre flottant avec les instructions SSE. Ça démontre également qu’il est illusoire d’essayer d’être plus malin que le compilateur en écrivant de l’assembleur (qui n’est pas optimisé par -Ofast!).
SSE ?
SSE, pour Streaming SIMD Extensions (équivalent de 3DNow!, depuis abandonné, chez AMD), est un set d’instructions processeur un peu spéciales, qui permettent de réaliser des opérations sur plusieurs nombres flottants en même temps. Comme le laisse penser le nom de la version AMD, cette extension était à l’époque pensée pour aider le calcul en virgule flottante, en particulier dans le contexte des applications en 3 dimensions.
En effet, le paradigme SIMD (single instruction, multiple data) signifie que la même instruction est appliquée à différentes données. Par exemple, soit les trois tableaux suivants
float a[N], b[N], c[N];
Si on souhaite réaliser l’addition des valeurs de a et b pour les stocker dans c, on écrirait le code suivant:
for(i=0; i<N; i++)
c[i] = a[i]+b[i];
ce qui, dans l’absolu, exécute N fois les instructions qui composent la boucle. Ici, une instruction SSE permet de réduire ce nombre d’exécution fois, ou est la largeur de l’unité vectorielle, c’est à dire le nombre de données que le processeur peut traiter en même temps. Par exemple, les premières instructions SSE permettait de traiter 128 bits à la fois, soit 4 float en même temps: le temps d’exécution de la boucle ci-dessus est donc réduit d’à peu près 4 fois avec une telle instruction. C’est d’ailleurs ce que gcc a fait dans le test ci-dessus, puisque toutes les instructions font partie du set original de SSE (les extensions suivantes ajoutent les double, et d’autres opérations qu’on retrouve dans des contextes bien précis, mais sans dévier de 128 bits). Bien entendu, les développeurs ne se sont pas arrêté là, et les extensions AVX2 et AVX512 proposent de traiter, respectivement, 256 et 512 bits à la fois (donc 8 et 16 float à la fois).
D’ailleurs, on peut forcer gcc à utiliser des instructions AVX avec -mavx, comme fait dans la dernière ligne du tableau ci-dessus. Et pour le laisser optimiser un maximum, on peut carrément utiliser -march=native. Ceci dit, ça n’est intéressant que dans le contexte du calcul intensif, puisqu’ici arrive déjà à quelque chose de potable avec -Ofast
Est ce qu’on peut faire encore mieux ?
TL;DR: oui, mais pas spécialement ici.
Mon intérêt pour Q_rsqrt n’est pas anodin. En effet, je suis (re)tombé sur cette fonction alors que je navigait sur les internets à la recherche de ressources pour le calcul intensif, que j’ai eu l’occasion de pratiquer durant ma thèse de doctorat. Or, le nouveau truc, en calcul intensif, c’est les GPUs, dont les performances sont relativement intéressantes s’ils sont bien exploités. Preuve en est, le prochain supercalculateur hexascale européen, LUMI sera principalement composé de GPU (des AMD Radeon Insctinct).
Dans le cadre du consortium des équipement de calculs intensifs belge (fédération qui rassemble les clusters des 6 universités francophones du pays), j’ai pour le moment (aout 2021) accès à deux types de GPUs de la marque Nvidia6: une Tesla V100, qui comme tout les produits de la gamme Tesla est un GPU expressément orienté pour le calcul intensif, et un GPU GeForce RTX 2080, qui est normalement prévue pour le grand public7 mais qui envoi du pâté tout de même (pour le calcul simple précision, c’est le plus puissant des deux).
Le code de test (pour rsqrt), écrit en CUDA (une surcouche du C++ pour écrire du code pour les GPU Nvidia) est disponible ici. La partie importante est la suivante:
cudaMemcpy(d_comm, floats_source, N_FLOAT *sizeof(float), cudaMemcpyHostToDevice);
int blocksize = 512;
int nblock = N_FLOAT/blocksize + (N_FLOAT % blocksize > 0 ? 1: 0);
rsqrt_vec<<<nblock, blocksize>>>(d_comm, N_FLOAT);
cudaMemcpy(floats_dest, d_comm, N_FLOAT *sizeof(float), cudaMemcpyDeviceToHost);
La première et la dernière ligne expliquent à elles seules les futures performances: en effet, pour que le calcul sur GPU aie lieu, il faut que les données soient disponibles dans sa mémoire vive, et la communication est évidemment l’étape limitante (le problème est le même en 3D "classique"). Autrement dit, pour qu’un calcul GPU soit rentable, il faut communiquer très peu et exploiter à fond les données une fois qu’elles sont communiquées (effectuer plusieurs séries de calculs avec).
Pour faire des calculs, on écrit des (compute) kernels, c’est à dire des fonctions qui suivent grosso modo le paradigme SIMD en effectuant une même série d’opération sur une série de données. C’est donc le même principe que les instructions SSE/AVX qu’on a croisé plus haut, sauf que les GPUs portent ce principe à l’extrême, en pouvant traiter d’énormes quantité de données "en même temps", grâce à une quantité proprement démentielle de coeurs de calculs (5120 pour le Tesla, 4352 pour le 2080 RTX). Ceci dit, ce n’est pas magique: comme on le voit aux lignes 4 et 5, il faut dire au GPU comment organiser les calculs: ceux-ci sont arrangés en "blocs" indépendants de blocksize thread qui collaborent étroitement (avec de la mémoire partagée, et une synchronisation entre autres). L’idée, c’est évidemment que chaque bloc traite une partie des données, et que les blocs soient assignés automatiquement par le GPU à des coeurs comme bon lui semble, tant qu’il reste des blocs à exécuter. Cela signifie que pour optimiser le code, on peut jouer sur différents paramètres (ce que je n’ai pas pris le temps de faire ici). Quant au kernel, c’est la fonction rsqrt_vec(), qui se borne à utiliser la fonction rsqrt que CUDA met à notre disposition.
Bref, voici les résultats. Encore une fois, le code a été exécuté 1000 fois, avec 100 000 000 nombres flottants générés (c’est 100x plus que précédemment, pour tenter de réduire l’effet de la communication), et je donne les moyennes. Notez que le temps reporté inclus la communication vers et depuis le GPU, pour comparer des choses similaires (ce qui nous intéresse, c’est le résultat).
| GPU | Performance |
|---|---|
| Tesla V100 @ 877 Mhz | 2.36 ns/float |
| GTX 2080 RTX @ 1545 Mhz | 1.01 ns/float |
Comme annoncé, le gain de performance n’est pas fou, et c’est probablement la communication qui domine le tout. Encore une fois, ça commence à devenir sérieusement intéréssant lorsqu’on utilise des kernels plus complexes
Sachez que si vous n’avez pas envie d’utiliser CUDA (par exemple parce que vous possédez une carte graphique d’une marque concurrente), il est possible d’utiliser d’autres méthodes plus "agnostiques". On peut citer deux alternatives: OpenCL (globalement équivalent à CUDA en termes de philosophie) et OpenACC, le second étant un équivalent de OpenMP, c’est à dire une méthode de programmation ou on indique (par des #pragma) les parties du code qu’on souhaitera que le compilateur parallélise (du mieux qu’il peut) au lieu d’écrire explicitement du code parallèle. À condition que le compilateur fasse correctement son boulot,8 on peut alors assez facilement paralléliser un code existant.
- La périodicité s’explique probablement très bien, mais je n’y ai pas réfléchi.↩
- Ce qui signifie qu’on sous-estime systématiquement la valeur
↩
- On peut encore réduire l’erreur en ajoutant des itérations de Newton : d’après Wikipédia, 3 suffisent amplement !↩
- Qu’on se comprenne bien: c’est "beau", mais on se permet bon nombre d’approximations pour que ça tourne "bien".↩
- … Et remplacé quelques mois après à cause d’un horrible problème hardware.↩
- Ceci n’est pas une pub: il se trouve qu’on croyait que LUMI allait être équipé en cartes NVidia et qu’on voulait prendre de l’avance. Grossière erreur
↩
- Et achetée avant la pénurie de 2021
↩
- C’est toujours en développement, et GCC est un peu à la traine pour OpenACC, il semblerait.↩
Au regard des performances respectives de Q_rsqrt et de rsqrt, le gain de performance du premier est aujourd’hui quasiment inexistant, donc son intérêt devient limité (surtout vu la perte de précision).
Quand à l’utilisation du GPU, ce n’est rentable que si plusieurs opérations sont appliquées de suite une fois les données placées en mémoire … Ce qui est totalement le cas dans les moteurs 3D actuels, ou les vertex sont sytématiquement offloadés sur le GPU (via, par exemple, la fonction glGenVertexArrays et consoeurs) pour être exploité ad nauseam. Dès lors, ça rend l’astuce d’autant plus inutile dans le cadre ou la fonction Q_rsqrt est apparue
Sources et autres curiosités
Outre les liens dans le texte,
- Wikipédia, comme d’habitude.
- Pour la dérivation de la première étape, j’ai choisi de suivre cet excellent post de Christian Plesner Hansen.
- Cet article qui détaille un peu l’histoire derrière la recherche de l’auteur de ce code.
Les codes sources et images sont disponibles sur Github, sous licence MIT.