L’autre jour, je m’ennuyais seul au volant de ma voiture. En regardant mon système de navigation, je me suis demandé dans quelles conditions je pouvais avoir le nombre de minutes restantes du trajet égal au nombre de kilomètres restants. On peut en faire un problème mathématique bien défini !
Le problème
Le problème du système de navigation est que le temps restant est une estimation. Mieux vaut changer le problème pour utiliser la distance parcourue au cours du temps depuis le départ. On cherche alors un moment où il s’est écoulé autant de minutes depuis le départ que de kilomètres parcourus.
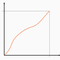
Le problème peut être modélisé comme suit. On dispose d’une fonction qui exprime la distance parcourue depuis le départ en fonction du temps et on cherche à savoir s’il existe une valeur de telle que . Graphiquement, le graphe de croise le graphe de la fonction identité.
Pour correspondre un minimum à la réalité physique, on doit ajouter un certain nombre de conditions :
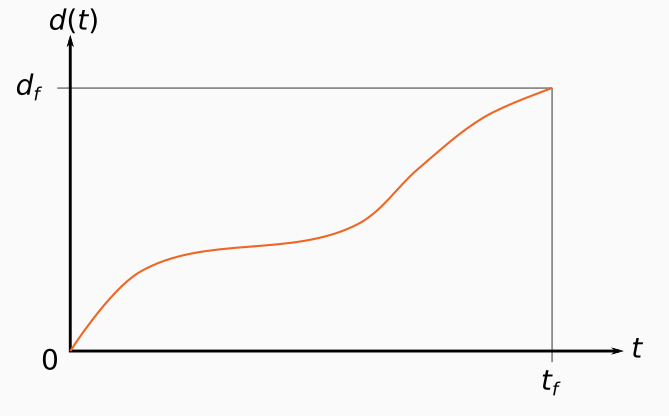
- la fonction est définie sur un intervalle , où 0 est l’instant de départ et l’instant d’arrivée ;
- la fonction est continue sur son intervalle de définition ;
- la fonction est croissante (pas forcément strictement) sur son intervalle de définition (on ne revient pas en arrière, mais on peut s’arrêter) ;
- et : on part du kilomètre 0 à l’instant 0 et on arrive à destination après une distance à l’instant .
On espère que ces hypothèses suffisent à trouver une réponse satisfaisante !
Explorer (et résoudre) le problème
Alors, une évidence est qu’il y a toujours une valeur telle que , puisque . On cherche à explorer les autres possibilités, celles non-triviales.
En griffonnant un peu, on se rend compte qu’il y a des configurations sans intersection du tout.

Intuitivement, il semble qu’il suffise d’avoir une valeur en dessous et une au-dessus de la courbe dans l’intervalle. Ou d’abord une au-dessus et ensuite une au-dessous.
Sous ces conditions, on a une application du théorème des valeurs intermédiaires. On considère la fonction telle que . S’il existe et tels que et , alors on a aussi et . Il existe donc une valeur entre et telle que et donc est la valeur recherchée, puisque .
On peut faire le même raisonnement en échangeant les signes de et .
Pour résumer, on a les cas suivants :
- si pour tout dans , ou si pour tout t dans , , alors pas d’intersection ;
- s’il existe et dans tels que et soient de signes opposés, alors il y a une intersection.
Rajoutons un peu de physique maintenant.
Et la physique dans tout ça ?
Quelques hypothèses physiques
Les hypothèses initiales oublient quelques éléments importants de la physique :
- ma voiture a une masse ;
- on suppose partir avec une vitesse nulle (ma voiture est garée) ;
- les accélérations infinies n’existent pas (mon moteur a une puissance finie !).
Sans rentrer dans les détails, ceci signifie que la fonction est non seulement continue, mais aussi à dérivée continue et donc que la vitesse est continue.
Conséquences sur le problème
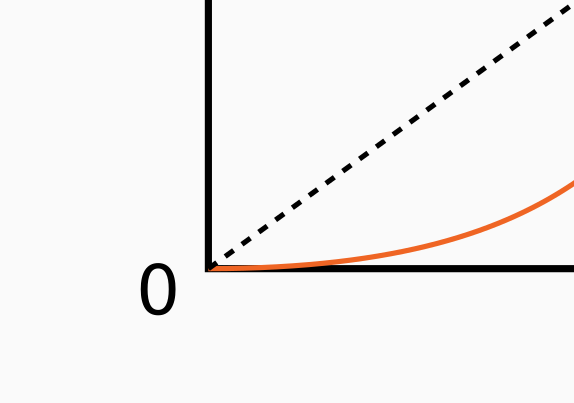
La conséquence pour notre problème est primordiale. On part d’une vitesse nulle, et elle varie continûment. Ainsi, toutes les courbes ressemblent à l’origine à ce qu’il y a ci-dessous ! On a une dérivée nulle, ce qui fait que le démarrage est toujours aplati.
Ainsi, par rapport à la section précédente, il suffit à un instant donné d’être au-dessus de la courbe pour finir par l’intersecter, puisqu’il y aura toujours un point en dessous au tout début.
On peut démontrer que est inférieure à l’identité localement avec des développements limités, je pense. L’exercice est laissé au lecteur.
Un cas particulier est par exemple si . En rajoutant des unités, je sais que si j’ai fait 70 km en 60 min, alors il y a eu un moment où le nombre de kilomètres et de minutes étaient égaux. Potentiellement 10 mètres après le départ, mais tout de même égaux !
Une petite condition nécessaire
Une autre idée qu’on tire de ça, est qu’il est nécessaire d’avoir une vitesse moyenne suffisante à un instant donné. Par exemple, avec un choix d’unités tel que ci-dessus, il faudrait avoir à un moment donné une vitesse moyenne de 60 km/ 60 min (soit 1 si on oublie les unités), la vitesse moyenne étant définie par .
On peut donner une petite démonstration : s’il existe dans l’intervalle tel que alors la vitesse moyenne sera égale à 1 à ce moment-là.
Aucune chance (avec ce choix d’unité) d’intersecter la courbe en vélo pour moi, tant que je ne suis pas champion de cyclisme sur piste !
Alors, me suis-je trompé quelque part ?
Il y a aussi des raffinements possibles, selon qu’on suppose la fonction strictement croissante, par exemple.