JVM-Rationals : Calculer dans ℚ avec la JVM

Salut les agrumes !

Le saviez-vous ? Il n’existe apparemment aucun moyen simple et standard de faire des calculs avec des nombres rationnes en Java. Il existe bien une classe Fraction chez Apache Commons qui est fonctionnelle mais très limitée, et une antique bibliothèque de sciences qui ne semble plus exister depuis des années… et un projet récent et inconnu dont je n’ai découvert l’existence qu’il y a quelques jours. Je passe sur les implémentations triviales donc très basiques qu’on trouve dans des coins du net.

C’est pourquoi je me suis mis en tête de faire ma propre bibliothèque pour ça. Plus parce que ça m’amuse et par intérêt technique (notamment ce que ça tire comme problèmes de performances) que pour vraiment l’utiliser, étant donné qu’en fait je n’en ai pas besoin.

Mon but était donc triple :

1. Faire une bibliothèque qui fonctionne et utilisable par tout le monde (donc un minimum testée).
2. Faire des tests de performance dessus, par curiosité.
3. Implémenter des fonctions qu’on ne trouve pas sur les quelques implémentations trouvées, en particulier les puissances rationnelles et la trigonométrie. Ce qui implique de gérer des nombres approximatifs, puisque rien que sqrt(2) est un nombre irrationnel.

L’avant-première version de tout ça est JRational (quelle originalité !) et c’est disponible sous licence Apache 2.0 sur Github.

C’est pas tout à fait une version 1.0.0 release (et donc ça n’est pas publié sur Maven Central / Sonatype), mais les jar et leurs signatures sont disponibles, tout comme la Javadoc.

Techniquement c’est du Java 11, même si rien ne s’oppose à ce que je puisse construire une version compatible Java 8 (il faut que je trouve comment faire avec ma version de Gradle qui tourne que sur Java 11+). Le code s’appuie massivement sur BigDecimal ce qui permet une précision arbitraire et virtuellement infinie (une paire d’entiers de deux milliards de nombres chacun…) mais du coup ne garantit absolument rien sur les performances.

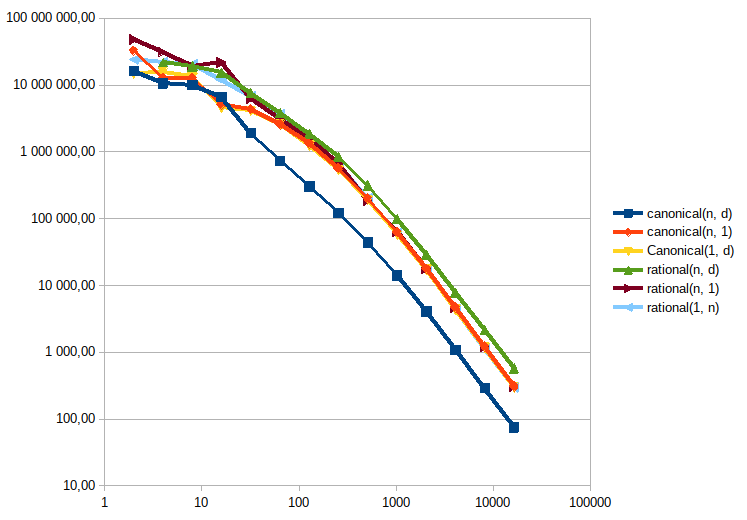
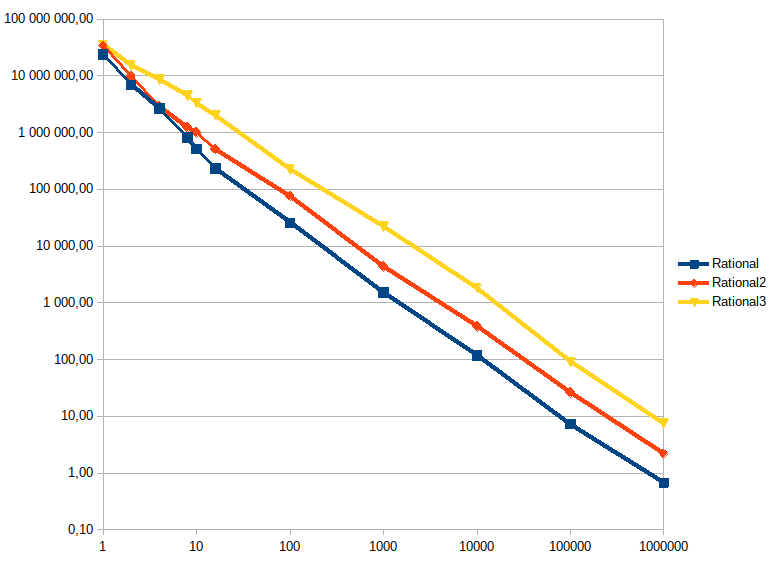
J’ai fait des tests de performance (ils sont ici, ./gradlew jmh pour les lancer, comptez plus de 3 heures pour la suite complète…). Ils montrent que les performances sont tout à fait acceptables pour des nombres de taille raisonnable (grosso modo O(1) jusqu’à 32 chiffres décimaux au total dans le rationel (numérateur + dénominateur), après quoi on est grosso modo en O(n) avec n le nombre de chiffres, en occupation mémoire comme en temps de calcul sur les opérations de base. Il y a une cassure dans la pente des performances, qui doit correspondre à un effet de la taille du cache du processeur : avant, 2x plus de chiffres = 2x plus de temps de calcul ; après, 2x plus de chiffres = 3 à 4x plus de temps de calcul (à la louche hein).

Les deux enseignement que j’en ait tiré, c’est que :

1. Forcer le stockage de la forme canonique n’est pas intéressant, parce que la pénalité de performances est trop importante (le passage sous forme canonique nécessitant de calculer un PGCD, ce qui est lent).
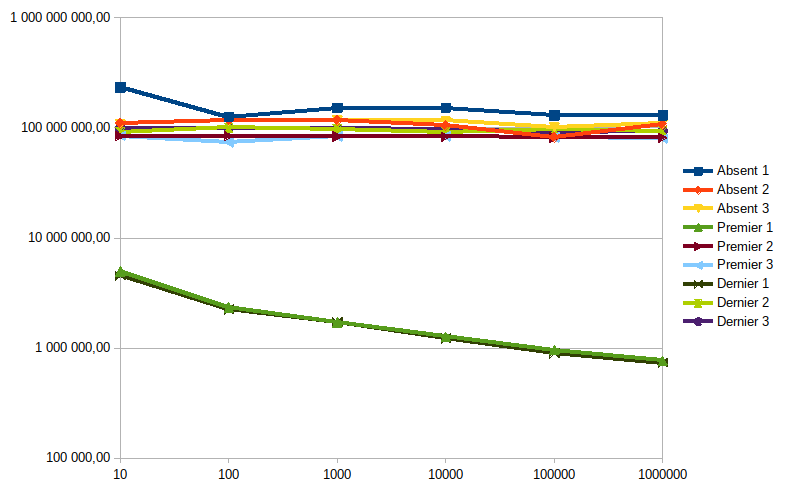
2. Par contre il faut une méthode pour calculer cette forme à la demande, parce que certains algorithmes produisent des nombres avec des très grands nombres de chiffres qui sont très facilement simplifiables. Par exemple celui-ci, sans la canonicalisation, ne finit pas pour cause de nombres de plusieurs millions de chiffres ; mais avec, le calcul se fait en quelques dizaines de ms.
3. Il faut aussi une méthode pour arrondir les valeurs qui deviennent trop précises pour leur propre bien (une chaine de calculs peut donner un rationnel exact, mais exprimé sous la forme de deux entiers gigantesques, de plusieurs milliers de chiffres chacun).

Bref, voilà où j’en suis aujourd’hui, je vise une v1.0.0 le WE prochain.

Je suis preneur de tous vos retours et pourquoi pas vos merge request, sur tous les sujets, y compris la gueule de l’API, les performances et les corrections d’anglais

Ah, et merci à @Aabu, @Quentin et @KFC pour leurs articles sur les flottants sur ZdS (ici, ici et là) qui m’ont donné des idées de tests pour vérifier les intérêts et limites des calculs de rationnels par rapport aux flottants IEEE-754.

PS : dans ce qui est prévu aussi, c’est au moins une version Kotlin (et peut-être Groovy ?) qui permet d’utiliser la surcharge des opérateurs. Parce que sur des nombres, c’est quand même vachement pratique.

Chouette projet.

En lisant le code je m’aperçois que le dossier .idea a été publié sur github (avec des fichiers par forcément utile à partager). C’est un oubli ?

Il faut que je vérifie, normalement le .gitignore utilisé gère ce cas et n’est censé partager que des fichiers utiles.

Vérifié, j’ai missclick à la génération du .gitignore et généré avec intellij+iml et pas intellij+all… faudra que je corrige ça.

Quelques commentaires à chaud en regardant le code:

1. Je ne comprends pas bien l’intérêt d’implémenter des opérations réelles (racines, trigonométrie) sur des rationnels. Pourquoi ne pas faciliter l’interopérabilité avec une bibliothèque de calculs réels en précision infinie, et basculer vers des réels si on veut ces opérations ?

2. Tu ne précises pas clairement la spécification de approximate(denominatorMax). Intuitivement on s’attendrait à obtenir la meilleure approximation possible avec un dénominateur inférieur à denominatorMax. Ton code ne fait sans doute pas ça, et de loin (mais je n’ai pas réfléchi très fort) on dirait qu’il perd inutilement de la précision. En particulier, il faudrait sans doute commencer par normaliser avant d’approximer. C’est une opération délicate, idéalement elle devrait (1) être spécifiée clairement et (2) avoir une implémentation bien expliquée qui justifie qu’elle respecte la spécification.

3. Les constructeurs of ne mettent pas en forme canonique, mais ils normalisent le placement du signe sur le numérateur. Est-ce vraiment utile ? Ça fait un petit surcoût à chaque opération qui n’est sans doute pas nécessaire. (Ne pas normaliser le signe rend abs un poil plus coûteuse, mais c’est une opération rare.)

4. Tu as fait le choix de dupliquer plein de méthodes (of en particulier, mais aussi ...Value par exemple) sur plein de types d’entrée proches mais différents, pour ajouter du confort à l’utilisateur. Est-ce vraiment utile ? Tu pourrais aussi gérer seulement le cas "un BigInteger" et "deux BigInteger", et laisser les utilisateurs faire les conversions de leur côté.

5. Pas convaincu par le wrapper identityOperation, ça fait beaucoup de tests pour des cas rares, et ça ne suffit pas pour exprimer toute la logique des "cas raccourcis" (multiply a toujours des tests à la main). Je pense qu’il serait aussi simple de calculer "normalement" les numérateurs et dénominateurs, et ensuite renvoyer this ou l’argument si on détecte qu’ils sont physiquement égaux au résultat. (BigInteger optimise déjà l’ajout de 0, et sans doute aussi (mais je n’ai pas vérifié) la multiplication par 1.)

6. La façon de calculer le hash est assez louche, tu vas hasher plein de nombres différents et proches sur la même valeur (par exemple : 3/4, 4/4, 5/4, 6/4, 7/4), ça sent les risques de comportements pathologiques sur les tables de hachage derrière.

7. Tu définis addAll en fonction de sum, j’aurais attendu l’inverse.

Merci pour ces remarques pertinentes !

Parce que ce qui m’intéresse le plus c’est précisément comment faire ces approximation. Ce projet, c’est principalement de la curiosité intellectuelle et méthodologique, qui me permet de répondre à des questions comme : comment on fait ce genre de calculs ? Qu’est-ce que ça implique en terme de performances ? Comment ça se comporte par rapport aux flottants standard ? Est-ce qu’écrire une bibliothèque pour quelque chose qui est souvent considéré comme plus ou moins trivial (la gestion basique des rationnels) est vraiment si trivial ? Etc. En fait je n’ai même pas de cas d’usage réel de cette bibliothèque

Si je trouve une bibliothèque de calculs réels en précision infinie en pur Java, ajouter une passerelle serait un développement futur intéressant.

2. Tu ne précises pas clairement la spécification de approximate(denominatorMax). Intuitivement on s’attendrait à obtenir la meilleure approximation possible avec un dénominateur inférieur à denominatorMax. Ton code ne fait sans doute pas ça, et de loin (mais je n’ai pas réfléchi très fort) on dirait qu’il perd inutilement de la précision. En particulier, il faudrait sans doute commencer par normaliser avant d’approximer. C’est une opération délicate, idéalement elle devrait (1) être spécifiée clairement et (2) avoir une implémentation bien expliquée qui justifie qu’elle respecte la spécification.

Sur ce point, c’est parce que je sais que ma méthode d’approximation actuelle est pourrie, en particulier parce qu’elle force le dénominateur fourni (s’il y a une approximation à faire) au lieu d’approximer au plus proche. Ça implique de trouver une méthode d’approximation qui fonctionne (en un temps raisonnable), chose à laquelle je n’ai pas assez réfléchi. Si quelqu’un a des pistes, je suis preneur.

En fait à l’origine tous les constructeurs mettaient sous forme canonique, mais c’est une catastrophe en terme de performances. Par contre normaliser le signe est pratiquement gratuit, et ne simplifie pas que abs mais aussi les égalités et les comparaisons.

Oui. Le confort de l’utilisateur ne coute pas grand-chose pour la lib, et fait beaucoup dans sa facilité d’utilisation – surtout si je conserve seulement les BigInteger en entrée, parce que ça devient très vite très verbeux en Java.

Je développe ma bibliothèque telle que j’aimerais bien qu’elle soit si je devais l’utiliser. Et ça faisait aussi partie du test : à quel point c’est un surcout d’ajouter du confort d’utilisation ?

On est d’accord, ce wrapper va très certainement sauter.

Là aussi je suis assez d’accord sur les risques, sauf que je suis un peu coincé par, d’une part le contrat de la paire equals()/hashCode(), et d’autre part le fait que je ne peux pas me permettre de normaliser les nombres à la création ou dans ces méthodes sous peine de faire exploser les performances en vol. En particulier, le problème vient de : a.equals(b) == true implique a.hashCode() == b.hashCode(), mais a et b peuvent être égaux et n’avoir aucun élément interne commun (par exemple : 2/4 et 3/6).

Si quelqu’un a une meilleure idée, là aussi je prends.

D’un point de vue logique pure, oui. D’un point de vue code, c’est plus logique dans ce sens, parce que addAll est une méthode d’objet mais sum est une méthode de classe, donc si je veux définir sum en fonction de addAll, il faut que je découpe ma collection, récupère le premier élément (ce qui n’est pas une opération triviale, vue que Collection n’est pas ordonnée, la notion de « premier élément » n’existe pas) et ajoute le reste de la collection.

Sur addAll: tu peux définir sum(xs) comme zero.addAll(xs).

Sur le hash: vu la spécification que tu te fixes, tu es obligé de canoniser la valeur avant de hasher.

Remarque: quand tu canonises une valeur, tu peux la récrire en place et donc gagner du temps sur les opérations suivantes sur la valeur. (En particulier hasher plein de fois un rationnel ne doit canoniser qu’une fois.) Peut-être que tu pourrais stocker un booléen "je suis déjà en forme canonique" pour éviter de canoniser plusieurs fois d’affilée la même valeur.

Sur l’approximation: je n’ai pas réfléchi non plus mais ça ressemble à un problème classique, avec en ligne une description de comment faire par une méthode assez simple (mais potentiellement coûteuse, si tu veux garantir l’optimalité de l’approximation). Je dirais de chercher sur internet "best rational approximation".

Mais même avec la spec actuelle "on utilise exactement le dénominateur fourni", je ne suis pas sûr que ton code actuel soit correct, les divisions d’entiers perdent beaucoup d’information.

Pour addAll et sum, je peux aussi laisser comme ça, ce qui fonctionne très bien et qui n’est qu’un détail d’implémentation. À moins qu’il y ait un intérêt à modifier la logique qui m’échappe complètement.

Pour hashCode(), ça va surtout demander des tests plus précis pour savoir à quel point la version actuelle pourrit les performances des classes qui l’utilisent. Parce que si j’explose les temps de toutes les utilisation pour en gagner un peu à la marge, ça n’est pas très intéressant

Pour l’approximation, il semblerait qu’il y a quelque chose à faire avec les fractions continues.

Oui, addAll peut rester légèrement plus verbeux et moins efficace que nécessaire, ça n’a sans doute pas beaucoup d’importance en pratique.

Pour le hash, c’est une question plus compliquée. Une fonction de hash ayant un mauvais comportement peut nuire aux performances en régime "normal", mais c’est surtout un risque de faille de sécurité (denial of service) en pourrissant un programme avec des entrées bien choisies pour générer beaucoup de conflits. (Cela dépend de si la communauté utilise en général des tables de hashages où les "buckets" de valeurs ayant le même hash sont cherchées en O(n) ou en O(log n). En Java il me semble qu’on est dans le cas O(n) où ça se passe très mal très vite.) Une fonction de hash qui génère des conflits inutiles, c’est avant tout une mauvaise conception dont les coûts sont difficiles à évaluer, et donc à mon avis qu’il vaut mieux éviter par principe — même dans les cas où on n’imagine pas vraiment de cas d’usages problématiques.

Pour sum/addAll, après tests, je n’ai aucune différence d’efficacité effective (les différence sont toutes dans les erreurs de mesure). Et la différence de verbosité se joue à une poignée de caractères. Donc je garde l’implémentation que je trouve la plus logique et lisible.

Benchmark          (size)   Mode  Cnt      Score      Error  Units
SumVsSum2.addAll       10  thrpt    6  65320,976 ±  585,561  ops/s
SumVsSum2.addAll      100  thrpt    6   3085,038 ±   51,613  ops/s
SumVsSum2.addAll     1000  thrpt    6     93,395 ±    1,007  ops/s
SumVsSum2.addAll    10000  thrpt    6      0,365 ±    0,003  ops/s
SumVsSum2.addAll2      10  thrpt    6  66836,846 ±  878,029  ops/s
SumVsSum2.addAll2     100  thrpt    6   3076,949 ±   31,093  ops/s
SumVsSum2.addAll2    1000  thrpt    6     93,063 ±    0,664  ops/s
SumVsSum2.addAll2   10000  thrpt    6      0,366 ±    0,003  ops/s
SumVsSum2.sum          10  thrpt    6  68822,368 ±  723,198  ops/s
SumVsSum2.sum         100  thrpt    6   3121,855 ±   18,989  ops/s
SumVsSum2.sum        1000  thrpt    6     95,146 ±    1,182  ops/s
SumVsSum2.sum       10000  thrpt    6      0,374 ±    0,016  ops/s
SumVsSum2.sum2         10  thrpt    6  62064,412 ± 1857,949  ops/s
SumVsSum2.sum2        100  thrpt    6   3133,087 ±   27,517  ops/s
SumVsSum2.sum2       1000  thrpt    6     95,291 ±    0,579  ops/s
SumVsSum2.sum2      10000  thrpt    6      0,379 ±    0,005  ops/s

Pour equals et hashCode, quand je parle de tests, je parle bien de tester les cas pathologiques (par exemple avec plusieurs millions d’entrées qui ont le même hashCode) et de vérifier ce que ça donne. Une autre solution serait d’esquiver le problème et de faire comme BigDecimal et de considérer que deux Rational ne sont égaux que s’ils ont le même dénominateur et le même numérateur (aujourd’hui ils sont égaux si les valeurs sont égales) – et là on peut juste faire un hashCode à partir des valeurs des champs de la classe. Par exemple pour BigDecimal, 2.0 et 2.00 ne sont pas équivalents, et il faut faire a.compareTo(b) == 0 pour tester l’égalité de valeur. Ce qui est pénible à l’utilisation et source de nombreuses erreurs. De plus dans le cas de BigDecimal, la notion d’« échelle » fait que la différence entre equals et compareTo me semble moins artificielle qu’avec la représentation des rationnels.

Bref, c’est pas un sujet trivial.

Alors : faites des tests. Les résultats pourraient vous surprendre.

Et donc, j’ai testé les formes 1, 2 et 3 du tableau ci-dessus.

Ça c’est juste la création de nombres.

Les tests suivants fonctionnent de la façon suivante : on crée une liste de n nombres, avec, i de 0 à n, de la forme (1 000 000 000 + i) / 1 000 000 000 (donc que des nombres très proches mais supérieurs à 1). Ces nombres ont la particularité, avec le code actuel, de tous donner un hashCode de 1, ce qui est donc le pire cas possible si on les mets dans une collection hachée (un seul hash pour toute la collection).

Là les résultats m’ont étonné, au point que j’ai vérifié le code et relancé une suite de tests (d’où les deux séries de points). En fait l’implémentation actuelle Rational est systématiquement plus lente que tout le reste et ce même pour des petites tailles de collection, surtout parce que le calcul du hashCode est plus compliqué que dans les autres implémentations. Et ça, je ne m’y attendais pas, et surtout pas à ce point (combiné à la collision des hash, on atteint très vite un facteur 10 par rapport à une insertion d’un rationnel optimisé pour les performances !).

On voit très bien que chercher une clé absente ou une clé dans une Map correctement indexée se fait très rapidement et en O(1) ; par contre le moindre défaut dans la répartition des hash a un impact catastrophique sur les performances, et ce même sur les petites Maps (un facteur 20 sur une Map de 10 clés). Par contre, la pénalité croit relativement peu vite avec la taille de la Map, en première approche je dirais que c’est du O(log(n)). Là aussi, je suis surpris : je ne m’attendais pas à un défaut aussi important aussi tôt, par contre je m’attendais à un perte plus importante sur les grandes Map.

Perso, avoir une fonction equals avec un comportement différent de CompareTo, c’est le genre de surprises auquel je m’attends en C, mais dans un autre langage, je m’attends à ce que la fonction fasse quelque chose de cohérent avec le type manipulé.

Après, en tant qu’utilisateur d’une lib de nombres, je m’attends à ce que les calculs soient rapides. Intuitivement, je privilégierais une solution où les nombres ne sont pas canoniques tant qu’on ne le demande pas. La comparaison de deux nombres est assez simple: a/b = c/d <=> a*d = b*c, en tous cas plus simple qu’une recherche de PGCD + division par celui ci, par contre, la table de hachage est un cas d’usage compliqué: je ne vois pas comment éviter de canoniser les nombres avant de les insérer ou chercher dans la table, et la structure est donc à réserver aux cas ou le coût de la canonisation est inférieur à celui de la comparaison avec chaque élément de la table. Cela dit, ça me choque pas, sur une lib de calculs, de regarder à combien de multiplications est équivalente une canonisation, et de recommander de ne pas utiliser les maps avec moins de valeurs que ce rapport. Ou sinon il faut faire une map qui ne repose pas sur un hash.

Cela dit, je me dis aussi qu’en ne canonisant jamais, les nominateurs et dénominateurs risquent de grandir à chaque opération mathématique, et, le temps de chaque opération dépendant de la taille du nombre, ça risque d’avoir un coût aussi à la fin. (cf point 2 de ton post initial)

Enfin bref, en tant qu’utilisateur, j’exclue les solutions 2 et 3. (Rien n’empêche d’avoir un nom autre que equals pour tester si deux nombres ont la même représentation, si c’est utile dans certains cas)

Je partirais sans aucun doute sur la solution 2. J’enlèverais complètement la fonction canonicalForm, et modifierais les opérations de base pour qu’une fraction soit toujours sous forme canonique. Mais je ne suis pas vraiment le public cible, je ne code pas en Java. Pour mieux répondre, il faudrait savoir à quels besoins tu essaies de répondre avec ta bibliothèque.

Je suis incapable d’imaginer un cas d’utilisation de rationnels à plusieurs milliers de chiffres, qui plus est avec un fort besoin de performances. Si on part du principe que les calculs commencent avec des petites fractions, il faut soit un très grand nombre d’opérations, soit des opérations très improbables (mise à la puissance 1000), pour en arriver là. Pour ma part, je n’ai jamais utilisé de rationnels de plus d’une douzaine de chiffres au dénominateur, et c’était déjà pour des calculs un peu fous, du type résoudre une EDO par perturbations jusqu’au dixième ordre…

Par contre, un cas d’utilisation que j’estime plus probable (peut-être à tort ?), c’est de faire la somme de beaucoup de petites fractions. Mettons que j’ai plusieurs milliers de fractions dont le dénominateur est inférieur à 10. Le dénominateur de la somme ne sera pas plus grand que 2520 sous forme canonique, et son numérateur aura autour d’une dizaine de chiffres au plus. Mais en l’état, ta fonction sum va manipuler des fractions à plusieurs milliers de chiffres, et aura probablement des performances exécrables (sans parler de la mise en forme canonique à la fin, si je veux afficher le résultat).

Après, rien n’empêche de garder le meilleur des deux mondes. Tu pourrais par exemple faire en sorte que par défaut les fractions sont sous forme canonique, mais avoir une option qui désactive ce comportement pour ceux pour qui ça pose un problème (ou inversement).

Remarques en vrac:

1. C’est facile à dire après coup, mais je ne suis pas surpris par les résultats de tes tests. (Je n’ai pas compris ce que montre le troisième graphique et je n’arrive pas à le lire, donc je ne dis rien de celui-là.) Canoniser tout le temps coûte cher, c’est connu, et ta fonction de hash est (soyons francs) pourrie, on l’a déjà dit aussi.

2. Pour une approche où tu mets tout le temps en forme canoniques, il doit y avoir des optimisations que tu n’as pas essayé. Par exemple, stocker l’information de si un terme est canonique ou pas, et récrire les nombres en place quand on le met en forme canonique (au lieu de renvoyer un nouveau nombre). Il y a aussi peut-être des algorithmes malins pour accélérer le calcul du GCD de nombres obtenus par calculs fractionnaires sur des fractions déjà simplifiées/canoniques.

3. Ce que j’avais proposé plus haut, c’est de mettre en forme canonique au moment du hash, en modifiant le nombre en place (donc: hasher plusieurs fois ne refait pas de travail inutile). C’est sûrement moins coûteux que mettre tout le temps en forme canonique, mais évidemment ça dépend des cas d’usage de hash dans un vrai programme, et donc ça va être plus difficile à benchmarker de façon représentative.

4. Comme l’a dit Jacen, ne jamais mettre en forme canonique tue aussi les performances, puisque tu te retrouves vite avec des numérateurs et dénominateurs énormes. Aujourd’hui par exemple "sum" est un peu une blague, le coût est au minimum quadratique en la taille du tableau d’entrée.

5. Et donc avec l’approche actuelle de ta bibliothèque, où la bibliothèque elle-même ne canonise jamais, c’est l’utilisateur qui a la responsabilité de canoniser au bon moment pour avoir les meilleures performances. C’est un sacré problème d’utilisabilité — faites le bien et vous aurez de bonne perf, soyez naï-f-ve-s et votre code va exploser. Mais en même temps, les gens qui ont besoin de ce genre de libs sont souvent des expert-e-s d’un domaine pointu, donc une approche "full control" peut se justifier.

6. Ça donne envie d’expérimenter avec des modes de mise en forme canonique "de temps en temps", qui se font automatiquement dans la bibliothèque, moins bien que des utilisateurs. Par exemple, "canoniser toutes les N opérations", ou "canoniser quand le dénominateur dépasse une certaine borne" (avec la borne qui est doublée à chaque dépassement, comme les tableaux dynamiques qu’on augmente exponentiellement, etc.). Pas facile mais intéressant comme questions, et sans doute déjà traitées dans la littérature sur le sujet, tu as regardé ? Idéalement tu aurais un truc avec un surcoût modeste, paramétrable, qui fait moins bien par défaut que les canonisations à la main des expert-e-s mais qui évite les gros problèmes si l’utilisateur ne fait pas les choses correctement.