- TD,
Je suis assez peu actif sur le forum mais certains me connaissent sans doute déjà depuis l’époque du SdZ ou depuis la publication de mon article sur le dessin d’une spirale de Fibonacci. Ce que vous ne savez sans doute pas, c’est mon intérêt pour la conception mécanique. C’est cet intérêt pour la mécanique qui m’a poussé à entreprendre le projet dont il sera question ici.
Introduction
Les maquettes du système solaire sont toujours impressionnantes. Pouvoir observer la position et le mouvement des planètes sur un objet physique fait toujours son petit effet. Les maquettes dynamiques qui reproduisent le mouvement relatif des planètes, qu’on appelle « planétaire » (en anglais orrery), qu’elles soient modernes ou anciennes, donnent toujours envie d’en posséder une. La société Eaglemoss l’a bien compris car elle propose depuis plusieurs années un planétaire en kit dont les pièces sont vendues chaque semaine dans un numéro. En réalité, Eaglemoss revend une maquette qu’on peut trouver ailleurs, notamment chez Orrerystore.
Des publicités pour le planétaire d’Eaglemoss ont été diffusées à la télévision au moment des fêtes de fin d’année. Elles m’ont tout de suite donné envie car c’était l’occasion d’avoir enfin mon propre planétaire. Même si ce genre de maquette est un peu bas de gamme et hors de prix (quoiqu’une maquette de ce type ne peut pas être bon marché), j’ai décidé d’acheter le premier numéro. Je découvre qu’après le planétaire comptant les huit planètes et deux planètes naines, il est proposé la construction d’un tellurion (c’est-à-dire d’un planétaire limité au Soleil, à la Terre et à la Lune). Finalement, renseignements pris, chaque maquette revient à 700 € et je commence à penser qu’elles ne sont pas si belles que ça et que, quitte à payer très cher, autant concevoir mon propre planétaire. Il ne serait certes pas aussi beaux que ceux exposés dans les musées, ni même aussi réussi que ceux d’Eaglemoss mais au moins j’aurais la satisfaction d’avoir réussi quelque chose.
Vous pouvez facilement trouver des images et des vidéos des planétaires d’Eaglemoss. En voici cependant une :
Genèse du projet
La décision de concevoir un planétaire terrestre a été prise courant janvier. Sachant pertinemment que j’aurais besoin de faire de la CAO, j’ai investi dans un ordinateur Dell Optiplex 745 (sorti en 2006) payé 45 € frais de port compris qui est dédié spécialement à faire de la CAO. Il tourne sous Windows 7 et arrive à faire tourner Solidworks 2016 avec 1 Go de RAM. J’ai récemment fait l’acquisition d’une carte graphique Nvidia GeForce GT710 pour améliorer les performances et je vais bientôt me ruiner dans 4 Go de DDR2 parce que j’ai toujours des messages me prévenant du swap pour la moindre petite chose.
Le but du projet était à l’origine de reproduire uniquement le mouvement de la Terre et de la Lune autour du Soleil sans reproduire les inclinaisons ni la révolution de la Terre. Un engrenage de quatre roues dentées (faux) a été calculé et j’ai très vite décidé d’ajouter l’inclinaison de l’axe des pôles de la Terre en ajoutant trois roues dentées indépendantes de l’engrenage pour conserver l’alignement de l’axe au cours d’une orbite. J’ai commencé à réfléchir sur la réalisation de la maquette elle-même en faisant des dessins et quelques calculs puis j’ai fait une pause.
Choix définitifs
Depuis le mois de mai, j’ai relancé mon projet et j’ai beaucoup travaillé. C’est à ce moment que j’ai compris mon erreur pour le premier engrenage et que j’ai décidé d’ajouter des complications. Après de multiples calculs, commencés et recommencés plusieurs fois, il a été décidé il y a peut-être deux semaines que mon planétaire terrestre aura les complications suivantes : inclinaison de l’axe de révolution de la Terre, inclinaison de l’orbite de la Lune, révolution de la Terre sur son axe, mouvement de précession de la ligne des nœuds de l’orbite de la Lune.
L’intégralité du mécanisme repose sur un engrenage à cinq étages :
- l’étage d’entrainement avec sa manivelle,
- l’étage pour la révolution de la Terre (étage J, J pour jours),
- l’étage pour la conservation de l’alignement de l’axe de révolution de la Terre (étage A),
- l’étage pour le mouvement de précession de la ligne des nœuds de l’orbite de la Lune (étage P),
- l’étage pour la rotation de la Lune autour de la Terre (étage L).
J’ai atteint la précision suivante pour les étages J, P et L :
| Étage | Valeur de référence | Valeur effective | Écart |
|---|---|---|---|
| J | 365,256363 jours par an | 365,256410 | 0,00001 % |
| P | 18,60 ans par tour | 18,60 | 0 |
| L | 13,368747 tours par an | 13.368750 | 0,00001 % |
L’étage A a une précision absolue du fait du mécanisme utilisé. Je ne connais par la précision habituelle des planétaires mais les valeurs obtenues me conviennent tout à fait.
J’ai fait en sorte que l’engrenage tienne sur une seule droite : tous les axes de rotation sont compris dans un plan, sauf bien sûr pour l’étage d’entraînement. Cela n’a pas été facile mais j’ai pu trouver une configuration satisfaisante.
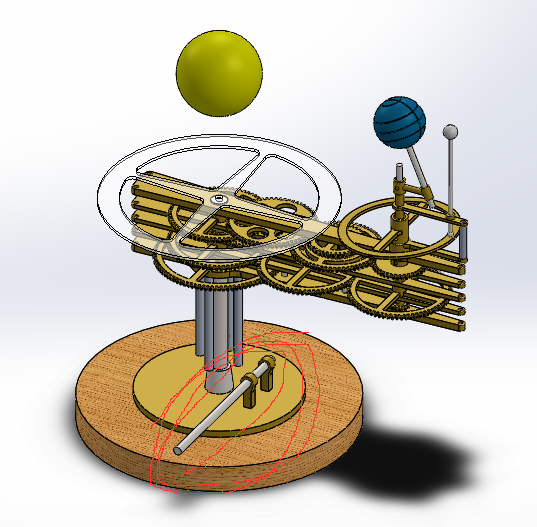
Après encore beaucoup de réflexion, je suis arrivé à ceci :
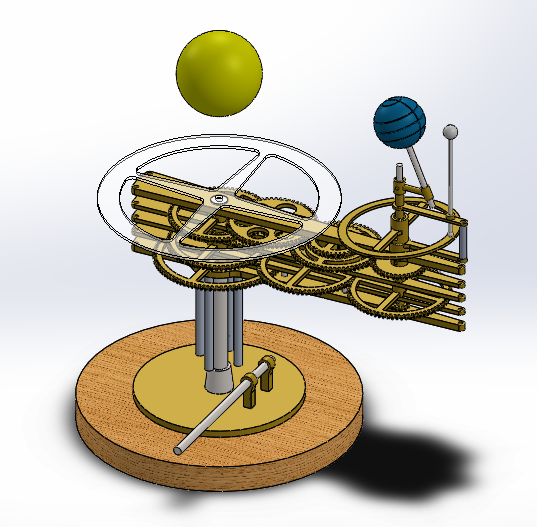
Ce qu’il reste à faire
La modélisation n’est pas encore tout à fait terminée. Je dois encore modéliser quelques roues dentées et d’autres détails comme les entretoises des platines de l’engrenage. Il faut également ajouter toute la visserie. Comme on peut le deviner sur l’image qui est directement issue de Solidworks, le planétaire est fait en laiton et en acier. La grande roue transparente est l’indicateur de la date. Le socle est en bois. Les matériaux peuvent encore être modifié et tout ce qui n’est pas lié aux engrenages peut encore être revu mais la version définitive ne devrait pas être très différente de ce qu’on peut voir aujourd’hui.
Une fois la modélisation terminée, je vais mettre toutes les pièces en plan. Cela me permettra de faire faire des devis pour enfin savoir combien je vais devoir payer. La fabrication ne sera pas effectuée par moi-même. Je n’ai ni le matériel ni le savoir faire pour travailler le métal. Je ferais appel à des entreprises d’usinage et je ferais le montage.
Je réfléchis actuellement à la possibilité de faire fabriquer plusieurs planétaires afin de les vendre. Si ça fonctionne, je pourrais me lancer dans une petite entreprise de conception et de fabrication de planétaire comme il en existe déjà quelques unes. Si vous êtes intéressé, n’hésitez pas à m’en parler.
Sources d’inspiration
Ma principale source d’inspiration est le travail réalisé par l’entreprise anglaise Staines & Sons Orrery Makers. Je ne nie pas une certaine ressemblance avec un de leurs modèles car c’est avec leurs vidéos que j’ai pu avancer dans la conception. J’ai toutefois l’intention de suivre mon propre chemin.
Plus modestement, le tellurion en bois de Holz Mechanik m’a donné l’idée d’ajouter une couronne d’indication de la date.
Un certain KenToonz a eu la bonne idée de filmer la fabrication de son propre planétaire :
Pour le plaisir, voici le planétaire de Jules Verne :
Il est bien sûr hors de question d’aller aussi loin pour le moment.


 (j'ai lu en diagonale, étant occupé irl). Ça mérite même une mise en une, ça.
(j'ai lu en diagonale, étant occupé irl). Ça mérite même une mise en une, ça.


 ! Je serais moi aussi curieux de voir un tuto sur les planétaires ou sur le génie mécanique. Bon courage à toi
! Je serais moi aussi curieux de voir un tuto sur les planétaires ou sur le génie mécanique. Bon courage à toi  !
! La mise en avant sur la page d’accueil me fait très plaisir. Ça me motive encore plus. N’hésitez pas à poser des questions sur la conception ou d’autres choses qui vous paraîtraient liées.
La mise en avant sur la page d’accueil me fait très plaisir. Ça me motive encore plus. N’hésitez pas à poser des questions sur la conception ou d’autres choses qui vous paraîtraient liées.

 .
.