La guitare et ses innombrables variantes comptent parmi les instruments de musique les plus populaires. Mais savez-vous comment une guitare produit du son ?
Les détails du fonctionnement diffèrent selon que la guitare est électrique ou acoustique, mais dans les deux cas, tout commence par la vibration d’une corde. Cette corde oscille d’une manière précise, qu’on peut prédire grâce à ses caractéristiques et aux lois de la physique.
Dans cet article, nous commencerons par décrire le comportement d’une corde de guitare. Nous déduirons ensuite une équation régissant le mouvement de la corde à partir d’un modèle simple de celle-ci. La résolution de l’équation nous permettra ensuite d’expliquer les comportements expérimentaux au regard du modèle.
Bien que la première partie soit assez accessible, des bases en physique et des notions mathématiques correspondant à la première ou deuxième année d’études supérieures sont nécessaires pour bien comprendre les parties suivantes.
- Expérimentations sur une guitare basse
- Modèle de la corde vibrante
- Confrontation entre théorie et réalité
Expérimentations sur une guitare basse
En musique, le son produit par une corde de guitare ou tout autre instrument est principalement décrit par :
- sa hauteur, c’est-à-dire le caractère aigu ou grave du son produit ;
- son timbre, c’est-à-dire les caractéristiques du son qui permettent de distinguer un instrument d’un autre lorsqu’ils jouent à la même hauteur ;
- son volume, c’est-à-dire le caractère bruyant ou non du son.
En physique, le même son sera décrit par des notions analogues :
- sa fréquence fondamentale, qui traduit la hauteur perçue de la note : une fréquence élevée correspond à une note aiguë et une fréquence basse à une note grave ;
- son spectre, qui caractérise à la fois l’intensité globale du son (le volume) et la répartition de l’intensité entre les différentes fréquences composant le son (le timbre).
À la guitare, on peut jouer différentes notes (et donc différentes fréquences fondamentales) de plusieurs manières :
- en bloquant la corde contre les frettes du manche, ce qui a pour effet de raccourcir la partie en vibration de la corde ;
- en serrant ou desserrant les mécaniques pour changer la tension de la corde ;
- en changeant la corde que l’on joue, ce qui revient à utiliser une corde plus grosse et donc plus lourde à longueur égale.
Influence de la longueur de la corde
Voyons l’influence de la longueur de la corde sur la fréquence fondamentale (ou hauteur) du son produit, en gardant la tension et l’inertie de la corde identiques.
À cette fin, j’ai réalisé une petite expérience avec ma guitare basse. J’ai enregistré le son produit par une corde (la corde de sol, la plus fine) pour différentes longueurs, et ai mesuré sa fréquence. Les résultats sont dans la figure ci-dessous.
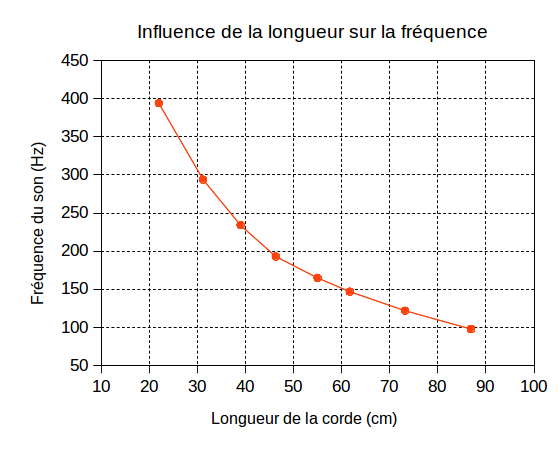
Ainsi, la fréquence semble être inversement proportionnelle à la longueur de la corde, toutes choses égales par ailleurs. Autrement dit, des cordes ayant les mêmes caractéristiques produisent des sons d’autant plus graves qu’elles sont longues.
Influence de la tension
Voyons l’influence de la tension de la corde sur la fréquence fondamentale (ou hauteur) du son produit, en gardant la longueur et l’inertie de la corde identiques.
N’ayant pas de moyen de mesurer en valeur absolue la tension de la corde, la mesure est exprimée en quart de tour dans le sens permettant de tendre la corde par rapport à une position de référence. Pour chaque position, on mesure la fréquence du son produit. Les résultats sont dans la figure ci-dessous.
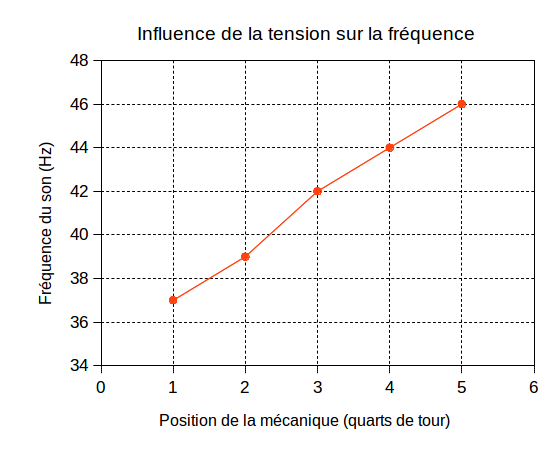
Ainsi, la fréquence augmente avec la tension de la corde, toutes choses égales par ailleurs. Autrement dit, plus une corde est tendue, plus le son qu’elle produit est aigu.
Influence de l’inertie de la corde
Voyons l’influence de l’inertie de la corde sur la fréquence fondamentale (ou hauteur) du son produit, en gardant la longueur et la tension de la corde identiques.
Il n’y a malheureusement pas de moyen facile de s’assurer que la tension est constante entre les différentes cordes. Cependant, il est raisonnable de supposer que les différentes cordes ont des tensions comparables. On mesure donc ici les différentes cordes de la basse de la plus grosse à la plus fine sans autre précaution. Les résultats sont dans la figure ci-dessous.
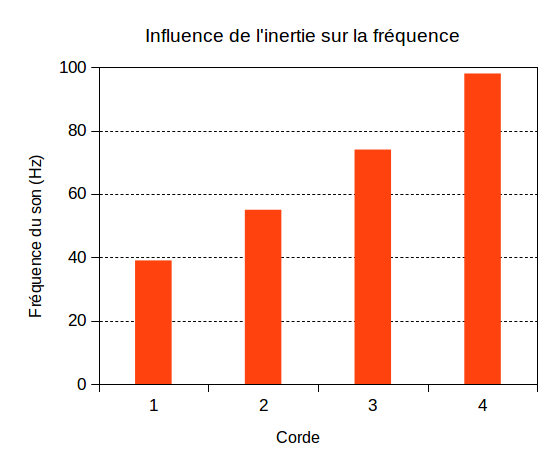
Ainsi, la fréquence diminue à mesure que l’inertie de la corde augmente, aux réserves déjà formulées ci-dessus près. Autrement dit, il semble que plus la corde est grosse, plus le son qu’elle produit est grave.
Modèle de la corde vibrante
Modèle de la corde vibrante
Au regard de la section précédente, notre modèle doit rendre compte des notions d’inertie, de tension et de longueur de la corde.
Nous choisissons de modéliser notre corde comme un fil de longueur , fixé à ses deux extrémités de sorte à y être immobile.
Ce fil est aussi sans raideur, autrement dit mou comme des spaghettis trop cuits. Ceci est une idéalisation, puisque les cordes de guitare ont tendance à se tenir droite d’elles-mêmes, ce qui est une des manifestations de leur raideur. On peut aussi voir une corde sans raideur comme une corde infiniment fine, qui n’aurait pas de comportement semblable à ceux d’une tige.
L’inertie de la corde est traduite par ce qu’on appelle la masse linéique, qui est tout simplement la masse de corde par unité de longueur. Une grosse corde aura une masse linéique élevée, alors qu’une petite corde aura une masse linéique faible. Le matériau est important : à forme égale, les cordes en métal ont par exemple une masse linéique plus élevée que les cordes en nylon. Notre corde aura une masse linéique (lettre grecque « mu »). Notre longueur de corde aura ainsi une masse égale à .
Notre corde sera tendue avec une force à chaque extrémité. Par ailleurs, nous supposerons que cette force est suffisamment élevée pour tenir la corde bien droite, comme la corde d’un arc, et non pas ballante comme une guirlande de Noël. Cette hypothèse permet de négliger le poids de la corde, puisque le mouvement de la corde ne sera pas affecté significativement par son poids. Autrement dit, jouer de la guitare la tête en bas ou allongé ne change rien au son produit.
Par ailleurs, nous négligerons l’interaction de la corde avec l’air, les fixations de la guitare, ainsi que les frottements internes à la corde. Ces mécanismes permettent de dissiper l’énergie de la corde et d’atténuer ses vibrations. En les négligeant, cela revient seulement à considérer que les vibrations durent un temps infini. Cela n’est pas absurde, puisqu’une note jouée sur une guitare basse peut durer plus d’une dizaine de secondes avant de voir son intensité baisser sensiblement.
Ces informations sont suffisantes pour commencer la mise en équations !
Mise en équations
Mise en place
Commençons tout d’abord par choisir un repère de l’espace de sorte que et soient à l’horizontale et à la verticale. Nous avons vu précédemment que la position de la corde dans l’espace n’est pas essentielle ; pour simplifier les calculs, nous la considérons horizontale, alignée avec l’axe des abscisses. Au repos, tous les points de la corde sont à l’altitude .
Si on déplace la corde de manière quelconque, les coordonnées des points vont varier a priori dans toutes les directions. Comme nous considérons une corde parfaitement souple, les différentes directions n’ont pas d’influence les unes sur les autres1, et nous nous contenterons d’étudier les mouvements selon le seul axe vertical .
Puisque la corde est fixée à ses extrémités et tendue, tout une gamme de mouvements est impossible. Notamment, la corde ne peut pas s’enrouler sur elle-même, claquer comme un fouet, ou bouger dans une direction ou une autre de plus de quelques fractions de sa longueur. Dans ces conditions, étudier le mouvement de la corde, c’est s’intéresser aux petites déviations de part et d’autre de la position d’équilibre, c’est-à-dire de l’horizontale. L’équation du mouvement de la corde s’obtient alors en étudiant le mouvement d’une petite section de corde en fonction de celui des sections de corde adjacentes.
On considère un point quelconque d’abscisse , qui a la possibilité de bouger verticalement, et dont la position est donc décrite par son altitude . Si on prend une petite portion de corde de longueur à commençant à la position sur la corde, on peut déjà exprimer sa masse à partir de la masse linéique de la corde : . La portion de corde a l’extrémité gauche à une hauteur et son extrémité droite à une hauteur . À chaque extrémité, la tension est tangente à la corde (par définition), et la droite tangente forme un angle avec l’horizontale à gauche et à droite.

La tension de la corde est choisie de norme . Comme il n’y a pas de mouvement global, cette valeur est la même aux deux fixations, sinon la corde se déplacerait sur l’axe des abscisses. Et comme la corde n’est pas élastique, la norme reste constante et égale à aux extrémités de toute portion de corde prise individuellement.
Ceci étant, on peut obtenir les coordonnées en projetant la tension sur les différents axes. Ainsi, on a pour l’axe des abscisses :
Et pour l’axe des ordonnées, on obtient :
Application du principe fondamental de la dynamique
On applique le principe fondamental de la dynamique au petit élément de corde selon l’axe vertical :
En utilisant les expressions de ci-avant, on obtient l’expression :
Pour exprimer , il faut trouver un moyen d’exprimer . Il est facile d’exprimer sa tangente, puisque la droite tangente a pour coefficient directeur la dérivée par rapport à :
Aussi, en utilisant la fonction réciproque, on obtient l’angle :
En appliquant le sinus, on trouve alors :
Cette expression est assez compliquée (et non linéaire), et il est possible de se simplifier la vie en la linéarisant, ce qui revient à faire l’approximation que les angles sont petits, et que donc l’est aussi. On peut alors faire un développement limité au premier ordre en de pour obtenir :
On utilise ensuite l’approximation pour faire la simplification suivante :
Similairement, on montre que :
Ainsi, en remplaçant dans (1) :
En développant au premier ordre selon , on a :
En remplaçant dans l’équation (2), on obtient :
Dans l’approximation des petits angles, on peut assimiler à , ce qui mène, en divisant par de chaque côté à :
On peut enfin adopter une forme plus normalisée et écrire notre équation finale :
où .
La constante a la dimension d’une vitesse. Il s’agit en fait de la vitesse de propagation des ondes sur la corde, comme nous le montrerons tout à l’heure.
Notre équation finale est une équation aux dérivées partielles appelée équation de d’Alembert unidimensionnelle, et il s’agit de la plus simple des équations qui permettent de mettre en évidence des comportements ondulatoires.
Cette grosse équation s’accompagne de deux petites équations traduisant l’immobilité des extrémités, qu’on appelle conditions aux limites.
Notre corde va vibrer !
Résolution dans le cas général
Forme de la solution
Il peut être montré que toutes les solutions de l’équation de d’Alembert peuvent s’écrire sous la forme suivante :
où est une fonction d’une seule variable dérivable deux fois.
Il est assez facile de vérifier que les fonctions de cette forme sont bien solutions.
Calculons le premier membre de l’équation de d’Alembert. Nous notons la dérivée seconde de .
Ainsi que le deuxième membre :
On en déduit que :
Ainsi, l’équation de d’Alembert est vérifiée et donc est solution.
présente la contrainte supplémentaire de devoir respecter les conditions aux limites :
Ceci impose donc en plus à la fonction d’être impaire :
et d’être 2L-périodique, ce qu’on déduit de la deuxième condition aux limites et de la parité :
La démonstration est cachée dans la balise ci-dessous.
De la première condition, on déduit, grâce à l’expression de : Ceci est équivalent à On en déduit par changement de variable () : est donc impaire.
De la deuxième condition, on déduit : Par réarrangement et changement de variable (), cela conduit à : Par imparité, on déduit que : En changeant une dernière fois de variable (), on obtient enfin : est donc 2L-périodique.
Interprétation de comme position initiale
La fonction correspond en vérité à la position initiale de la corde. En effet, à l’instant initial , la solution s’écrit de la manière suivante :
Autrement dit, il suffit de connaître la position initiale de la corde pour avoir une solution de l’équation ! La position initiale est décidée par le guitariste, lorsqu’il joue la corde. Cela signifie que le choix de la position initiale va influencer également le son, en plus de la tension, masse linéique et longueur.
Interprétation de comme vitesse de propagation
La solution générale est constituée de deux termes.
- Le premier correspond à une perturbation qui avance vers les croissants, qu’on qualifie par conséquent d’onde progressive,
- Le deuxième correspond à une perturbation se propageant vers les décroissants et est qualifié d’onde régressive.
Voyons pourquoi.
Si on considère seulement la perturbation correspondant au premier terme, un point de la corde à l’instant aura pour hauteur :
Après avoir attendu un temps , est-ce qu’il existe une position où se trouverait la perturbation de hauteur ? On peut répondre à cette question en résolvant l’équation pour :
Assez facilement, on trouve pour solution :
Cela signifie qu’après un temps , la perturbation se retrouve à une distance de la position initiale. Ainsi, correspond à la vitesse de propagation de la perturbation sur la corde ; vous pouvez vérifier d’ailleurs que la dimension est bien celle d’une vitesse. Comme est positive, la perturbation avance vers les positifs, et c’est pour ça qu’on parle d’onde progressive.
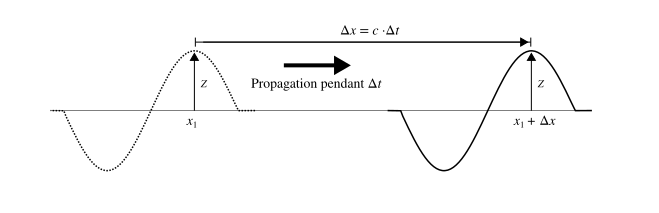
En faisant un calcul similaire pour le terme , on trouve que la vitesse de propagation de cette perturbation est et il s’agit donc d’une perturbation qui avance vers les décroissants, on parle ainsi d’onde régressive.
On voit alors que si la corde est plus tendue, augmente et donc la vitesse de propagation également, car . De même si la masse linéique est plus petite, alors la vitesse de propagation augmente également.
Solutions particulières et caractéristiques du son
La résolution dans le cas général nous a donné des contraintes sur la position initiale et une interprétation de comme vitesse de propagation, mais ne nous a pas beaucoup éclairé sur les caractéristiques du son en termes de fréquence.
Solutions harmoniques
Pour en apprendre plus sur le modèle, nous allons résoudre l’équation pour un type particulier de positions initiales : les sinusoïdales. Cette famille de solution correspond au cas particulier des fonctions de la forme :
Cette fonction correspond à une forme initiale en forme de sinus, dont les sommets sont à une hauteur et deux sommets consécutifs séparés d’une distance . On appelle la longueur d’onde.
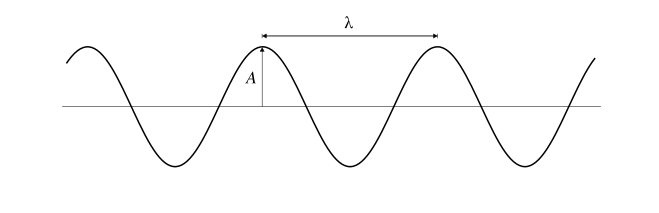
Il s’agit donc de solutions de la forme :
où est un réel quelconque et est contraint par les conditions limites.
On peut remarquer qu’on a toujours la forme générale, appliquée à la fonction .
Pourquoi cherche-t-on les solutions harmoniques, c’est-à-dire sinusoïdales ?
Quand on s’intéresse à des phénomènes périodiques (vibrations, ondulations, ondes sonores, …), il est très courant de chercher des solutions harmoniques.
Chercher de telles solutions est courant, parce que dans le cadre de certains outils mathématiques, comme le développement en série de Fourier, les sinusoïdes peuvent être interprétées comme des briques élémentaires des signaux périodiques plus complexes.
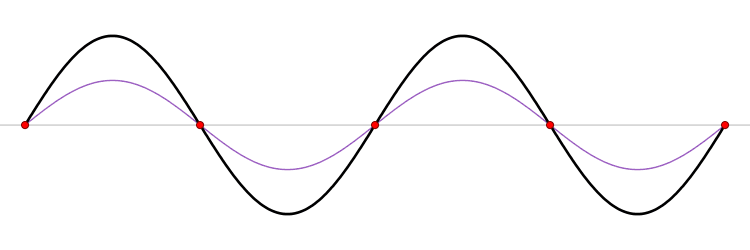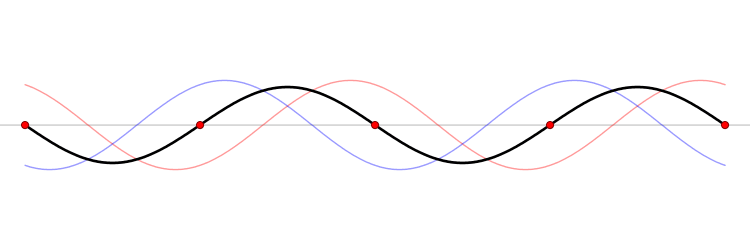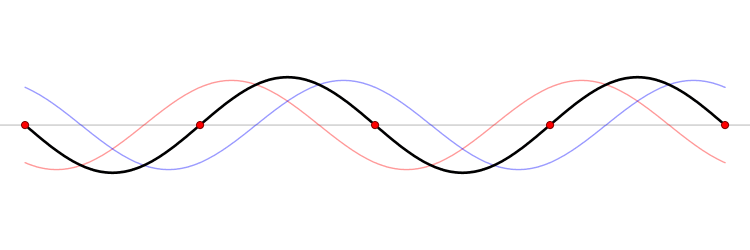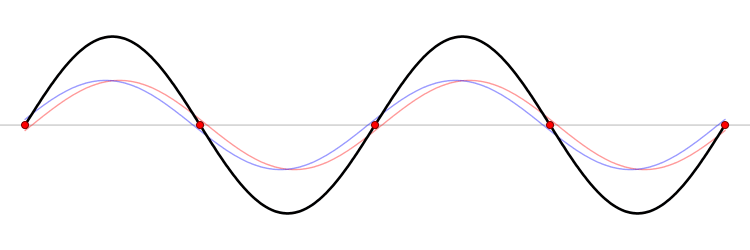
Onde stationnaire
L’expression actuelle n’est pas très pratique à utiliser, mais il existe une simplification avantageuse en utilisant l’identité trigonométrique suivante :
Grâce à celle-ci, on peut transformer la solution comme suit :
Cette forme est très intéressante, car on peut remarquer les choses suivantes :
- Il n’y a plus de couplage entre le temps et l’espace. On peut en effet voir cette onde comme une sinusoïde dont l’amplitude varie avec le temps, mais sans que les creux et bosses ne changent de place. On parle d’onde stationnaire : il s’agit d’une onde car elle est formée par la combinaison de deux ondes qui se propagent en sens inverses, et elle est stationnaire car la combinaison des deux ondes est telle qu’il n’y a pas de phénomène de propagation global.
- La longueur d’onde et la vitesse de propagation sont liées à la fréquence. En effet, le cosinus correspond à une oscillation de fréquence telle que . On en déduit que , c’est-à-dire que la vitesse, la fréquence et la longueur d’onde sont liées.
Conditions aux limites
Au début de cette section j’avais dit que était a priori quelconque. Notre équation de d’Alembert s’accompagne cependant de conditions aux limites, qui vont imposer des contraintes sur .
L’immobilité à gauche de la corde se traduit par :
Cette équation est toujours vérifiée, car les sinusoïdes sont impaires, et elle n’impose donc pas de contraintes particulières.
Voyons voir si l’immobilité à droite nous apporte plus d’information :
Pour vérifier cette équation pour tout , il faut donc :
On peut restreindre le paramètre à l’ensemble des entiers naturels non-nuls car :
- est positive et que la longueur d’onde est par définition positive, donc est un entier naturel,
- le cas particulier peut-être éliminé, car il correspond à une longueur d’onde infinie, c’est-à-dire une corde totalement plate.
En fin de compte, on a toute une famille de vérifiant :
On peut utiliser le fait que pour exprimer cette contrainte sur la fréquence plutôt que sur la longueur d’onde :
En remplaçant la vitesse de propagation par son expression, on obtient la très intéressante relation :
Cette expression nous renseigne de plein de manières.
-
À fixé, on retrouve le comportement phénoménologique de la guitare !
- Pour une masse linéique et une longueur donnée, la fréquence augmente avec la tension de la corde. On a une relation de la forme .
- Pour une tension et une longueur donnée, la fréquence diminue avec l’augmentation de la masse linéique. On a une relation de la forme .
- Pour une tension et une masse linéique donnée, la fréquence est inversement proportionnelle à la longueur de la corde. On a une relation de la forme .
-
À longueur, masse linéique et tension constante, l’ensemble des fréquences possible est indexé par . Autrement dit, il n’est pas possible d’avoir toutes les fréquences imaginables, mais seulement un sous-ensemble de fréquences précises, une par valeur de .
Décomposition d’une solution quelconque en solutions harmoniques
Toute solution va pouvoir être décomposée comme une somme de solutions particulières harmoniques. Cela signifie que, sous certaines conditions en général remplies en physique, il est possible de considérer la déformation de la corde comme une superposition de petites déformations sinusoïdales, et ce quelle que soit la position de la corde. Physiquement, cela signifie que l’on va déterminer l’intensité de chaque fréquence dans le son produit par une corde de guitare, et donc pouvoir connaître le spectre du son, uniquement à partir de la position initiale de la corde !
Ce petit tour de passe-passe mathématique est permis grâce aux séries de Fourier, qui permettent de décomposer un signal périodique (la déformation initiale de la corde) en une somme, éventuellement infinie, de sinusoïdes.
Sans s’étendre excessivement sur cet outil mathématique, il est possible de l’utiliser dans notre cas comme suit. Si est une fonction 2L périodique et impaire, alors il existe des coefficients tels que :
Les sont calculés comme suit :
On peut également utiliser le fait que pour écrire :
La solution correspondant à la position initiale est alors :
On voit que l’on a bien une somme d’ondes stationnaires ayant pour fréquences . La valeur de chaque correspond à l’intensité de chaque fréquence et donc au spectre du son émis par la corde.
- Sur une corde non souple, on sent l’influence des différentes directions assez facilement. Prenez le premier câble électrique qui vous passe sous la main et tordez-le à angle droit. Cela est assez facile normalement. Maintenant, maintenez votre angle droit et tentez de tourner d’un quart de tour une des branches de l’angle : vous devez sentir qu’il est plus difficile de tourner désormais. Les mouvements selon les différentes directions ne sont pas indépendants.↩
Confrontation entre théorie et réalité
Nous avons vu un grand nombre de formules, un peu rébarbatives pour certaines et informatives pour d’autres. Nous savons déjà que les phénomènes concernant la tension, la masse linéique et la longueur sont vérifiés.
Dans cette partie, nous nous attaquons au spectre, et tenterons de voir si la décomposition en solutions élémentaires se retrouve dans l’expérience !
Pour cela, nous allons étudier une corde qu’on joue au niveau du corps de l’instrument. La corde adopte dans ce cas une forme de triangle dont le sommet est sur le côté. La longueur et la hauteur de corde correspondent grossièrement à un cas où l’on joue la corde la plus fine de manière « normale ». La corde présente alors l’allure ci-dessous.
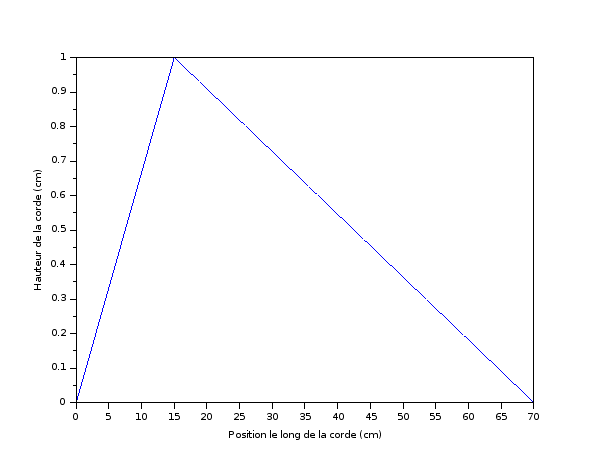
En faisant la décomposition de Fourier, on trouve les coefficients ci-dessous, pour les premières harmoniques.
| k | (mm) | |
|---|---|---|
| 1 | 7.5042 | |
| 2 | 2 | 2.9335 |
| 3 | 3 | 1.2049 |
| 4 | 4 | 0.3264 |
| 5 | 5 | -0.1071 |
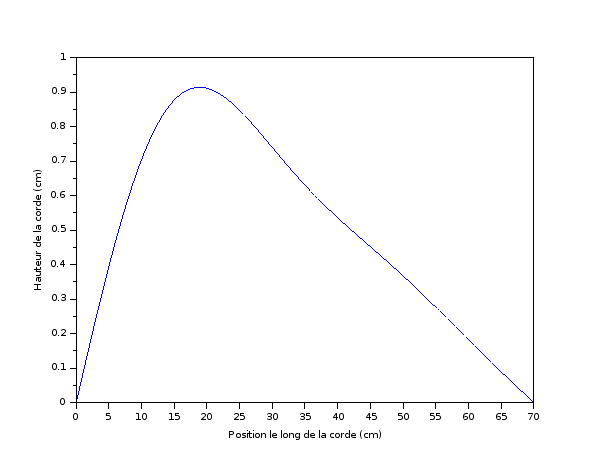
On remarque que les premières harmoniques sont les plus fortes, et que les contributions à partir de la quatrième harmonique sont très faibles. Les coefficients diminuent en effet assez rapidement avec l’augmentation de . Le troisième terme vaut environ un sixième du premier et le quatrième un vingt-cinquième du premier.
On peut voir que les termes élevés comptent peu en utilisant seulement les premiers termes de la série de Fourier pour reconstruire une approximation de la forme de la corde. On trouve la courbe ci-dessous.
Vérifions si notre modèle physique prédit le spectre correctement. J’ai fait un enregistrement avec ma basse comme dans la première partie, mais cette fois-ci, en prenant soit de jouer la corde à 15 cm du chevalet et je trace le spectre du son ainsi produit, c’est-à-dire l’intensité des différentes fréquences qu’il contient.
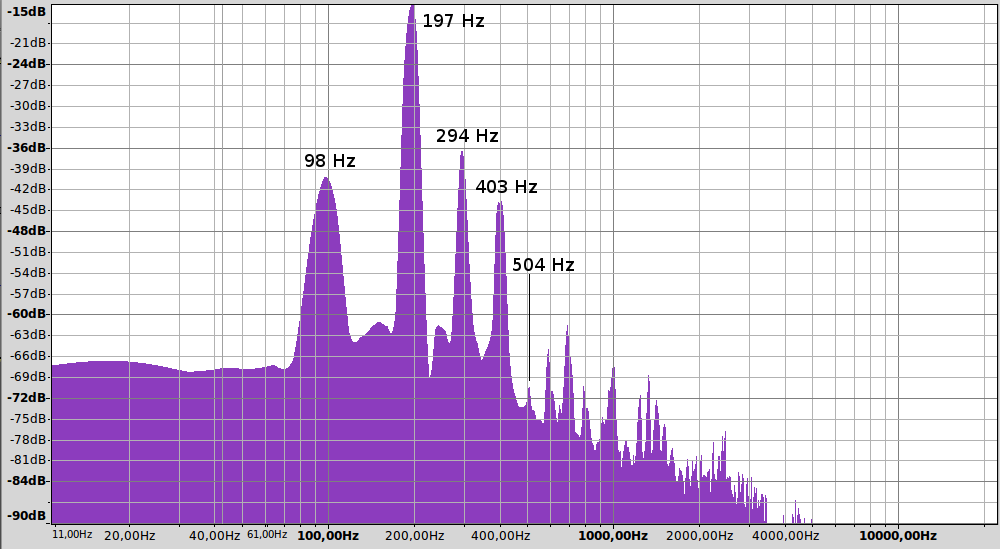
On remarque que la première fréquence est d’environ 100 Hz, ce qui correspond à la fréquence fondamentale. On retrouve ensuite toutes les harmoniques (environ 200 Hz, 300 Hz, etc.), jusqu’à des fréquences élevées.
Contrairement au calcul théorique, la fréquence fondamentale n’est pas la plus forte. Ce n’est pas tellement surprenant, car le son enregistré au micro n’est pas simplement dépendant de la vibration de la corde, mais aussi du corps de la basse, du préamplificateur, de l’amplificateur, et surtout du microphone. Étant donné que mon micro est de basse qualité et dédié à la voix, il semble normal qu’il ait des difficultés avec les basses fréquences.
On retrouve cependant le comportement théorique sur les autres harmoniques, dont l’amplitude décroît rapidement, mais qui sont présentes jusqu’à des ordres élevés. On peut en effet voir des pics pour les harmoniques d’ordre 10 voir même 20 avec de bons yeux.
Le modèle de la corde vibrante est un modèle simple. Il s’agit en effet de décrire comment les vibrations se propagent sur une corde attachée à ses extrémités. En prime, il s’agit d’un modèle à une seule dimension ; on ne prend pas en compte le fait que la corde est en réalité un volume et non pas un fil infiniment fin.
Ce modèle présente bien sûr des limites, liées à la manière dont les vibrations sont amplifiées pour parvenir à nos oreilles. Mais, il permet de décrire assez bien le comportement expérimental des cordes de guitare. On voit l’influence de la tension, de la masse linéique, de la longueur très facilement. Au-delà même de ça, il est aussi possible de prévoir la répartition des différentes fréquences dans le son produit, et cela en fonction de la position à laquelle on joue la corde si on le souhaite !
L’extension du problème de la corde vibrante à une membrane vibrante est possible, et on obtient alors une équation similaire, mais avec deux variables spatiales, pour représenter toute la surface de la membrane. Mathématiquement, on peut ainsi étudier des tambours de n’importe quelle forme (circulaire, carrée, etc), ce qui offre une grande richesse par rapport aux simples cordes vibrantes. Cette richesse a amené certains mathématiciens à se demander s’il était possible d'entendre la forme d’un tambour (vidéo en anglais)…
Miniature de l’article : basse Stagg photographiée par Elmschrat, sous licence CC-BY-SA 4.0 (source).
Merci à Holosmos pour la validation et les suggestions mathématiques.









