Vous allez voir qu’on va ré-exprimer ce qu’on a vu au chapitre précédent sous une forme légèrement différente, mais qui va nous permettre de travailler de manière plus efficace avec ces variables propositionnelles. Vous allez voir que c’est moins compliqué qu’il n’y parait.
L’algèbre de Boole, telle qu’utilisée ici, n’est en fait qu’une façon légèrement différente de formaliser les choses : on se base en fait sur la théorie des ensembles (en travaillant avec un ensemble à deux éléments, ), et on rajoute deux opérations (ou plutôt deux lois), qui sont le et le . L’objet qu’on crée alors s’appelle une « algèbre de Boole à deux éléments » et possède différentes propriétés intéressantes qu’on va exploiter ici.
- Propriétés de l'algèbre de Boole
- Fonctions booléennes
- Simplifier une forme normale : la méthode de Karnaugh
- Simplifier une forme normale : la méthode de Quine-Mc Cluskey
Propriétés de l'algèbre de Boole
Dans l’introduction, on a parlé d’ensemble et de lois. Ça, c’est pour que les matheux soient contents … Mais de quoi on parle ?
Déjà, on parle d’ensemble, ce qui signifie que toute opération sur un élément de cet ensemble doit être un élément de cet ensemble (pas forcément le même). Ici, on travaille avec un ensemble composé de deux éléments, donc le choix est assez restreint.
Mais quelles sont ces opérations ?
- La disjonction, . Cette opération est équivalente au connecteur OU, donc si .
- La conjonction, , qu’on peut également écrire ou encore plus simplement . C’est l’équivalent du connecteur ET, donc si .
Et mine de rien, le fait qu’on utilise ces deux opérations et la théorie des ensembles veut dire qu’on a déjà un certain nombre d’axiomes (de règles) associés :
| Nom | Axiome pour | Axiome pour |
|---|---|---|
| Neutre | ||
| Inverse | ||
| Commutativité | ||
| Distributivité |
Ici, , et sont des variables propositionnelles telles qu’on les a rencontrées au chapitre précédent, on parle également d’atome1 dans le cadre de l’algèbre de Boole.
- L’axiome du neutre est assez logique au vu de ce que vous avez appris en math : il existe, pour chacune des deux opérations, une valeur qui ne change pas le résultat. Ces valeurs sont d’ailleurs les mêmes que d’habitude, puisque n’importe quoi multiplié par 1 ou additionné de 0 reste le même.
- L’axiome suivant (aussi appelé axiome de complémentation) signale la présence d’un inverse. Ça a l’air très compliqué, mais ça nous permet en fait de retrouver quelque chose qu’on a déjà vu : pour tout atome, , il existe sa négation, qu’on note ici (certains notent aussi ). Comme on l’a vu au chapitre précédent, et . Là où c’est moins intuitif, c’est que dans les mathématiques classiques, la multiplication par l’inverse ( pour la multiplication) donne 1, et l’addition de l’inverse ( pour l’addition) donne 0, alors que c’est l’inverse ici.
- Les troisième et quatrième axiomes, la commutativité et la distributivité, sont assez classiques pour la multiplication, moins pour l’addition (l’addition n’est pas distributive en algèbre classique). Mais ce n’est pas l’addition classique, donc ça tombe bien
Bref, on a des règles légèrement différentes de ce qu’on a l’habitude de voir, mais qui sont néanmoins logiques au vu de ce qu’on a vu au chapitre précédent. Par ailleurs, ces règles sont définies d’une manière particulière, au vu d’une propriété intéressante de l’algèbre de Boole, la dualité : si on définit une règle pour un des deux opérateurs, on peut obtenir la règle pour l’autre opérateur en interchangeant et . Ainsi, si on reprend le premier axiome pour , , on voit qu’on obtient bien l’axiome correspondant pour (son dual) en remplaçant par et par .2
À noter qu’on nomme littéral un atome ou son opposé. Ainsi, est une disjonction de deux littéraux, et .
De là, on tire un certain nombre de propriétés3:
| Nom | Propriété de | Propriété de |
|---|---|---|
| Associativité | ||
| Involution | de même | |
| Idempotence | ||
| Élément absorbant | ||
| Loi de De Morgan | ||
| Théorème d’absorption | ||
| Théorème d’allègement | ||
| Théorème du consensus |
Ces propriétés vont se révéler utiles lorsqu’on va travailler, juste en dessous, sur des fonctions booléennes. Par ailleurs, vous pouvez facilement vérifier que ces propriétés respectent la dualité exprimée ci-dessus.
- Pour rappel, je suis chimiste de formation, donc ça me fait sourire
↩
- Ça va même plus loin que ça, puisque si on réussit à prouver une propriété pour un opérateur, son dual est également prouvé.↩
- Les preuves des différentes propriétés sont disponibles à différents endroits sur internet, par exemple ici (en). Vous pouvez par ailleurs vous amuser à les vérifier en écrivant des tables de vérité, même si certaines sont triviales.↩
Fonctions booléennes
Pour la faire courte, une fonction, c’est une application qui fait correspondre un ensemble à un autre, c’est-à-dire qui, à un objet mathématique dans un ensemble de départ, en fait correspondre un autre dans l’ensemble d’arrivée :
qui signifie que la fonction est une application qui fait correspondre à un ensemble de éléments (un -uplet) de l’ensemble à un ensemble de éléments de l’ensemble . Dans le cas qui nous occupe, on va travailler avec des fonctions de , donc des fonctions de variables en entrées et qui donne un résultat unique (0 ou 1).
Micmaths a déjà consacré un excellent cours aux fonctions, que je vous conseille de relire pour vous rafraîchir la mémoire, le cas échéant
Encore une fois, un mot très compliqué pour désigner ce qu’on a déjà rencontré dans le chapitre précédent sous le terme de formule. Une fonction booléenne, c’est donc une série d’atomes liés entre eux par des opérations vues plus haut. Par exemple, la formule est « traduite », dans l’algèbre de Boole, par . De par les axiomes qu’on a vu plus haut, on sait déjà que c’est équivalent à .
Mais on peut complexifier les choses et travailler sur des fonctions booléennes beaucoup plus complexes (la complexité n’ayant pour limite que votre imagination), telles que
Une telle fonction, bien que tout à fait correcte, peut être réécrite sous deux formes :
- Forme normale conjonctive (FNC) : la fonction est exprimée sous forme d’une conjonction de formes disjonctives : , avec la clause disjonctive, c’est-à-dire une disjonction de littéraux (). Si tous les atomes sont présents (sous forme de littéraux) dans chacune des formes disjonctives, on parle de forme normale (ou canonique).
- Forme normale disjonctive (FND) : la fonction est exprimée sous la forme d’une disjonction de formes conjonctives (donc , ).
Pour obtenir de telles formes, il est nécessaire de faire porter la complémentation sur les variables (en utilisant la loi de De Morgan si nécessaire), puis d’utiliser la distributivité de sur (pour une forme disjonctive) où de sur (pour une forme conjonctive).
Dans le cas de la fonction donnée plus haut, on aurait:
où la dernière ligne est bien une forme disjonctive, mais pas canonique (on obtient en fait la fonction simplifiée, comme on le verra plus loin). On voit qu’il est normalement nécessaire de se servir des différentes propriétés pour arriver à une expression qui est relativement plus simple à traiter.
Obtention des formes normales
Il existe cependant un moyen d’obtenir les FND ou FNC facilement en travaillant sur la table de vérité. On s’intéresse aux différents cas pour , et et on regarde ce que cette fonction retourne :
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Obtenir la FND
Pour la FND, on s’intéresse aux cas pour lesquels la fonction vaut et pour lesquels on écrit la conjonction des littéraux (qu’on appelle des minterms) correspondante :
- et . Ce premier cas donne la conjonction , et la table de vérité de la fonction nous dis que celle-ci donne 1 pour résultat lorsque , et , or .
- et , soit et on a la conjonction , soit et on a la conjoinction .
La forme normale disjonctive (FND) est obtenue en prenant la disjonction de ces différentes conjonctions, donc . On aurait ceci dit pu l’obtenir comme suis:
(mais c’est quand même plus facile avec la table de vérité)
Obtenir la FNC
On s’intéresse aux cas où la fonction vaut 0 (qu’on appelle des maxterms) , et de la même manière, on note les différentes conjonctions correspondantes. On obtient alors
qui correspond à l’inverse de la fonction . Si on en prend la conjonction, la propriété d’involution assure que , mais la loi de De Morgan nous permet alors d’obtenir:
… Qui est bien la forme normale conjonctive (FNC).
Simplifier une forme normale : la méthode de Karnaugh
Obtenir la forme normale est certes pratique, mais le but final est en fait de simplifier cette forme, afin d’avoir le moins d’opérations possibles à faire. On a vu plus haut qu’il était en fait possible, à l’aide des différentes propriétés, de simplifier une fonction booléenne, néanmoins, il existe une manière de faire plus simple, basée sur les diagrammes de Karnaugh (ou tables de Karnaugh), qui a le bon goût d’être une méthode graphique.
La méthode
Tout d’abord, il faut savoir comment construire ces fameux diagrammes de Karnaugh : il s’agit d’une autre manière de représenter la table de vérité ci-dessus.
- Pour trois variables, un diagramme contient 8 cellules (16 cellules pour 4 variables).
- Chacune de ces cases correspond à une série de valeur pour les différentes variables : ainsi, pour 3 variables, et , on aurait par exemple, le triplet (donc et ).
- La règle est que quand on passe d’une case de ce diagramme à une autre, seule une variable peut changer de valeur (la numération suit un code de Gray). Ainsi, on peut passer de à mais pas à . Dès lors, on ordonne le diagramme de telle manière à ce que les deux premières colonnes aient une valeur de , tandis que ce sont les colonnes du milieu qui auront une valeur pour égale à 1. Comme ça, on a la série pour et . On fait de même pour les lignes (c’est tout à fait arbitraire).
- De manière évidente, un triplet ou quadruplet donné ne peut se retrouver que dans une seule cellule.
On obtient par exemple les diagrammes suivants :
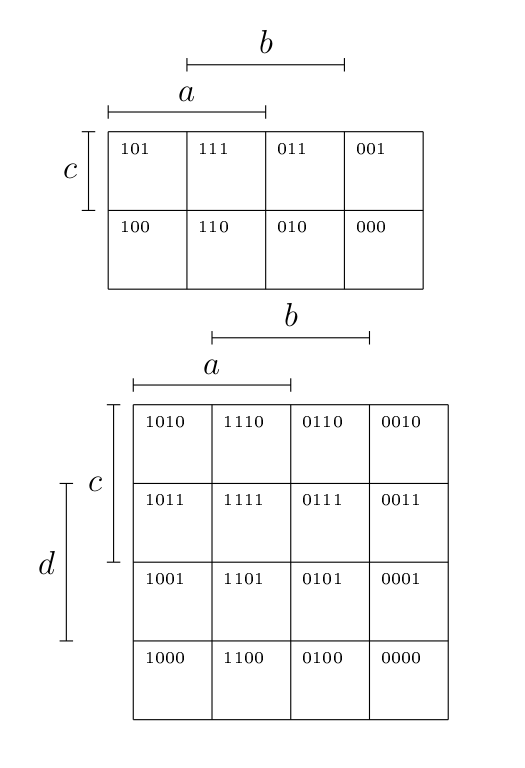
Il suffit alors de remplir ce diagramme en plaçant 1 aux endroits où la fonction vaut 1, 0 ailleurs. Il suffit de reprendre la table de vérité et de mettre ce qu’il faut au bon endroit. Dans le cas de notre fonction, on obtient le diagramme suivant.
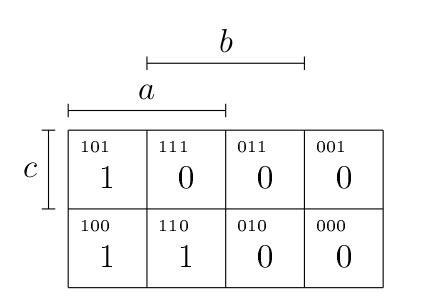
La règle de simplification est assez simple : si deux cellules contenant la même valeur sont contiguës, c’est qu’elles peuvent être simplifiées. En effet, ces deux cellules contiennent forcément une même série de littéraux, , multipliée par un atome, , nié dans une cellule et non-nié dans l’autre. Dès lors,
Ce qui signifie qu’on élimine les atomes qui varient d’une cellule à l’autre, ou encore qu’on ne conserve que les littéraux qui ne changent pas. De la même manière, on peut simplifier 4 cellules contiguës (en ligne, en colonne ou en « carré «) d’un coup, voir également 8 cellules contiguës, si elles sont présentes (2 lignes ou 2 colonnes dans un diagramme 4x4, du coup). On peut considérer plusieurs fois une même cellule, puisque par idempotence.
Simplifier la FND
Pour obtenir une fonction disjonctive simplifiée, on travaille sur les endroits du diagramme où la fonction vaut 1.
Dès lors, dans le cas de , on constate que les deux cellules de la première colonne valent 1 (entourées en vert), ainsi que les deux premières cellules de la deuxième ligne (entourées en bleu).
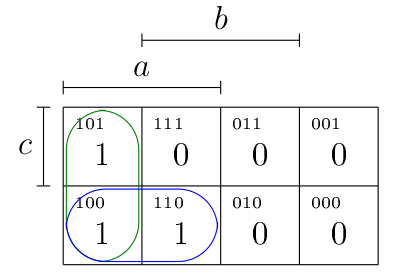
- Pour la simplification des cellules entourées en vert : il s’agit de la formule , où on voit que c’est qui est l’atome nié et non nié. On obtient donc la conjonction
- Pour la simplification en bleu : , puisque est l’atome nié et non-nié dans ce cas.
On obtient dès lors la forme disjonctive simplifiée suivante : , comme prévu.
Simplifier la FNC
On travaille sur la partie du diagramme où la fonction vaut 0, ce qui permet en fait d’obtenir une forme simplifiée pour sous forme disjonctive, puis forme conjonctive simplifiée par la loi de De Morgan, ainsi qu’expliqué plus haut.
Au niveau de notre exemple, on constate qu’on a une série de 4 cellules contiguës (en rose), et deux cellules contiguës à la première ligne, en deuxième et troisième colonne (en orange).
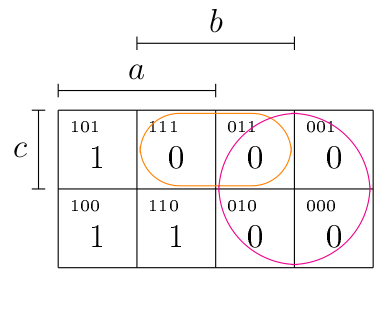
- Pour la simplification en rose : , car on voit que sont niés et non-niés les atomes et , ce qui permet de tous les simplifier.
- Pour la simplification en orange : , puisqu’ici, c’est l’atome qui est nié et non-nié.
On obtient alors , ce qui permet d’obtenir une forme conjonctive simplifiée comme suit :
À noter qu’on aurait pu l’obtenir à partir de la forme disjonctive simplifiée en mettant en évidence .
Attention, le diagramme de Karnaugh est cyclique !
Et j’insiste :
Puisque l’ordre est arbitraire (tant qu’on respecte la règle du 1-seul-changement-de-valeur-d’une-cellule-à-une-autre), ce qui signifie qu’un bord du diagramme est en fait le début de l’autre bord, et que ce qu’on considère comme plat est en fait un tore.

Il faut donc bien regarder sur les côtés si un plus grand groupement n’est pas possible.
Voyons ça sur un second exemple : soit une fonction qui donnerait le diagramme de Karnaugh suivant.
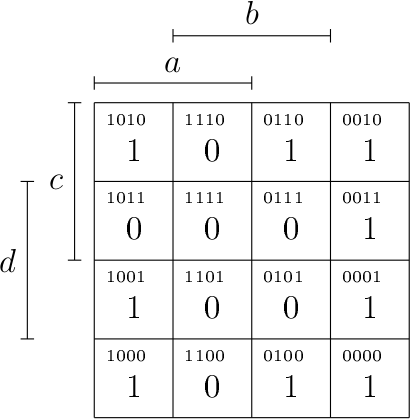
Le nombre de possibilité pour former des groupes de 2 ou 4 cellules est considérablement accru à cause de ça. Par exemple, on peut très bien proposer les groupements suivants.
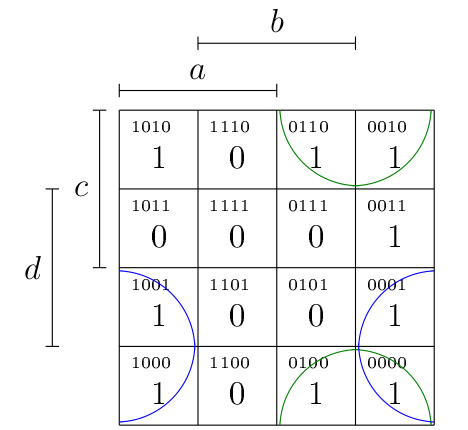
Du coup, la stratégie va être :
- D’abord tenter de faire des groupes de 8, puis de 4 et puis de 2 cellules (et attention à ce qui se passe sur les bords, donc).
- Pas besoin de former un groupe si toutes les cases en questions appartiennent déjà à d’autres groupes.
Sachant cela, quelle serait la forme disjonctive et conjonctive réduite correspondante au diagramme donné plus haut ?
Afficher/Masquer le contenu masqué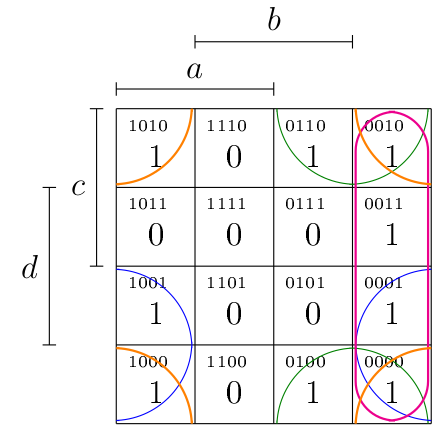
Groupes de 4 cellules :
- En vert : ;
- En bleu : ;
- En rose : ;
- En orange : .
Une forme disjonctive simplifiée serait donc :
.
Pour ce qui est de la forme conjonctive, on groupe les cases de la manière suivante.
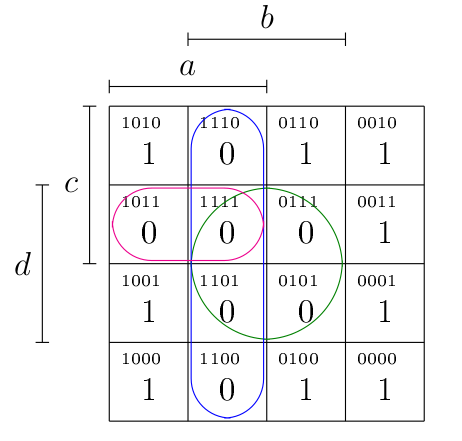
On trouve donc que , dès lors, une forme conjonctive simplifiée est :
.
Ce n’est pas des plus simple, mais il faut toujours chercher à faire des groupes avec la plus grande taille possible.
« Don’t cares » ?
Un autre cas intéressant à traiter, c’est le cas où on ne s’intéresse pas au résultat pour certaines valeurs. L’exemple classique, c’est l’afficheur 7 segments, qui permet d’afficher les nombres sur une calculette ou un réveil digital (ou un écran du même type).
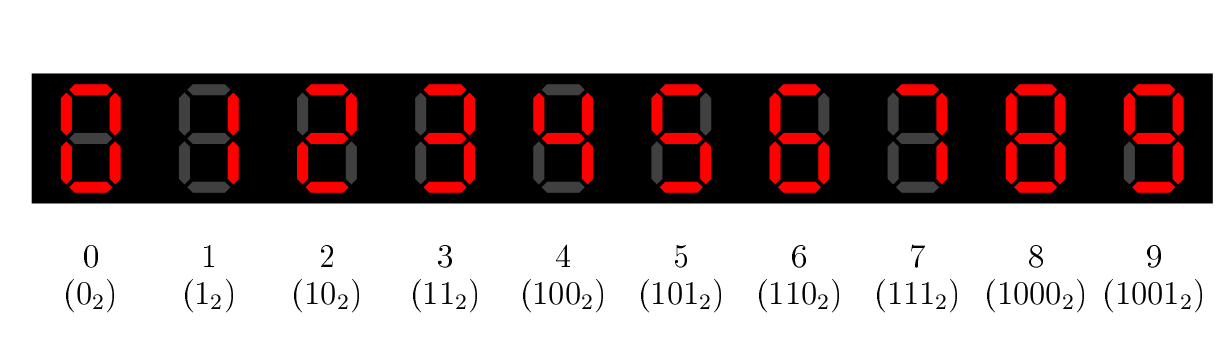
Chaque « segment » est une LED qu’on allume ou éteint en fonction du chiffre qu’on souhaite afficher. Ces segments sont désignés par des lettres, par facilité.
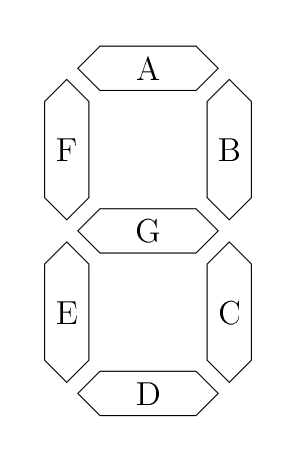
Il s’agit d’un bon exemple, puisqu’on pourrait par exemple se demander, en fonction du nombre à afficher, s’il est nécessaire d’allumer, disons, le segment G. On voit dans l’image ci-dessus que pour représenter les nombres de 0 à 9, 4 bits sont nécessaires, appelons-les , , et . Par exemple, pour représenter 5, on aura et . Et la suite, c’est évidement une petite table de vérité, où on va chercher la fonction , qui vaudra 1 quand le segment G sera allumé, 0 sinon.
| Nombre | |||||
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 |
Oui, mais quand on va réaliser notre table de Karnaugh, quelle valeur mettre pour, par exemple, (11 en décimal) ? L’afficheur ne peut pas afficher de nombre plus grand que 9, évidement1 … Eh bien on s’en fout (c’est un comportement indéterminé, qui ne devrait pas arriver), on met un don’t care, qu’on va symboliser par un « X ».
Notez qu’on écrit également cette fonction
où (pour minterms) sont les valeurs pour lesquelles la fonction vaudra 1 et (pour don’t care) sont les valeurs qui ne nous intéressent pas. L’écrire en binaire (dessous) ou en décimal (dessus) revient évidement au même. Les termes qui ne sont pas cités (0, 1 et 7) sont ceux pour lesquels la fonction vaut 0.
On a donc le diagramme suivant.
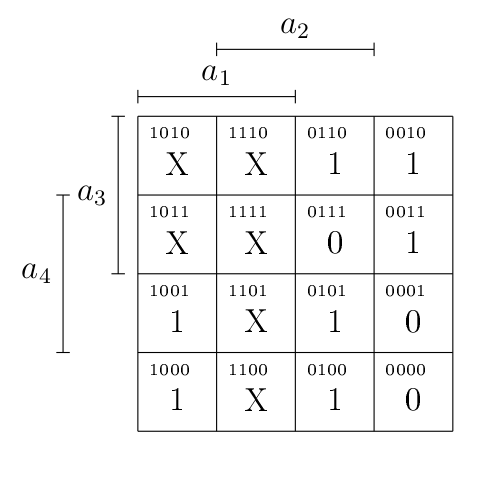
L’avantage des « X », c’est qu’ils peuvent valoir 0 ou 1, au choix. Voilà qui ouvre évidement plus de possibilités de simplifications ! Je vous laisse réfléchir au résultat.
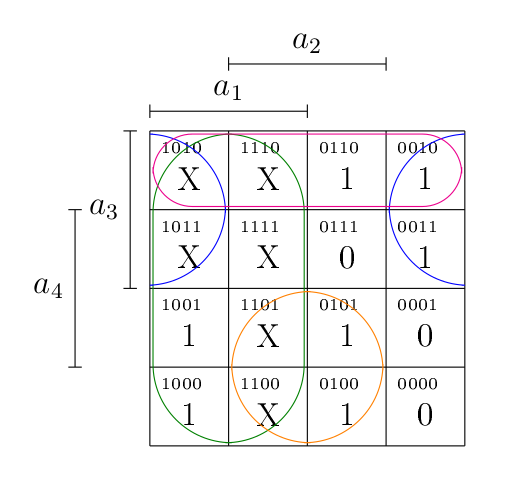
Dès lors,
Évidement, rien ne vous empêche de faire le travail pour les autres segments.
Conclusion
La méthode de Karnaugh est relativement simple à mettre en place et fonctionne bien … Pour peu que le nombre de variables soit faible (puisqu’il y a possibilités pour variables). On va voir une seconde méthode légèrement plus simple à expliquer à un ordinateur pour qu’il fasse le taf’.
Néanmoins, si vous voulez vérifier vos résultats, le site http://www.32x8.com/ le permet de manière simple et efficace, et ce jusqu’à 8 variables si vous êtes courageux (par contre il est en anglais).
- En fait, certains exploitent les nombres suivant pour afficher les 7 premières lettres de l’alphabet (a, b … f) afin de faire de l’hexadécimal. Mais pour l’exemple, on disait que.↩
Simplifier une forme normale : la méthode de Quine-Mc Cluskey
Présentation de l’algorithme
La méthode de Quine-Mc Cluskey se déroule en deux temps : la recherche de termes dit « générateurs » et l’élimination des termes redondants (suivi éventuellement de la méthode de Petrick pour choisir entre termes). C’est un algorithme taillé pour être traduit en code informatique, mais dont l’explication n’est pas très compliquée (son application est par contre un peu fastidieuse). Voyons ça sur un exemple.
Reprenons la fonction pour le segment G et voyons comment générer sa forme simplifiée. Pour rappel :
Première étape
Nous allons commencer par regrouper les minterms (et les valeurs « X ») en fonction du nombre de 1 qu’ils contiennent. Par facilité, on va aussi les classer par ordre croissant à l’intérieur de chaque groupe :
On va ensuite combiner les termes qui ne varient que d’un chiffre, pour générer l’ordre 1. Par exemple, (notation pour minterm 2) peut être combiné avec , puisque ceux-ci ne varient que d’un chiffre. On écrira ce nouveau terme (comme dans la méthode de Karnaugh, ces termes peuvent être combinés de telle manière que disparaisse, d’où le 1). À noter qu’une fois qu’un terme est utilisé, il est marqué comme tel (mais peut être réutilisé si nécessaire). L’avantage d’avoir trié en fonction du nombre de 1, c’est que les termes du groupe 1 ne peuvent être combinés qu’avec les termes du groupe 2, ceux du groupe 2 uniquement avec ceux du groupe 3, et ainsi de suite. En effet, on élimine les termes redondants, et donnant la même chose que , il n’est pas nécessaire de le garder.
Dès lors, on obtient :
Pour générer l’ordre 2, on regroupe les termes (encore une fois, avec ceux du groupe suivant) de telle manière à ce que les soient à la même position, et que, encore une fois, le reste ne diffère que d’un chiffre. Ainsi, peut être combiné avec puisque le est en dernière position dans les deux cas et le chiffre qui varie est le premier. On aura donc . Pareil, notez qu’on obtient la même chose en combinant avec , d’où . Une fois encore, comme ce terme est redondant, on l’élimine. Notez que des termes redondants contiennent à chaque fois les mêmes minterms de base (ici : 2, 3, 10 et 11), il suffit donc de garder la combinaison dans l’ordre croissant et d’éliminer toutes les autres. Les autres termes de l’ordre 2 ne peuvent pas être combinés.
Finalement, on refait l’étape une troisième fois (et dernière fois, comme il n’y a que 4 variables). Dans ce cas-ci, on peut grouper avec pour obtenir . On obtient également la même chose en combinant avec , donc pas besoin de le retenir. Et finalement, on obtient encore une fois la même chose avec et .
Conclusion de tout ça, on se retrouve avec les termes suivants : , , , (termes non utilisés de l’ordre 2) et . Il s’agit des termes générateurs (ou implicants premiers), la première étape de l’algorithme est complète. On peut constater que le terme avait déjà été obtenu par la méthode de Karnaugh plus haut. En effet, et même si c’est pas forcément visible, la méthode employée reste la même (par contre, elle est plus facile à expliquer à un ordinateur) !
À noter qu’un implicant (en), c’est une combinaison de minterms d’une fonction booléenne donnée. Par exemple, si on a une fonction , alors ou sont des implicants de . Un implicant premier, c’est un implicant qu’on ne peut plus simplifier par les lois de l’algèbre de Boole (qu’on ne peut pas exprimer avec moins de littéraux). Par exemple, est un implicant premier de , par contre ne l’est pas : on peut soit retirer le pour obtenir l’implicant premier précédent, soit retirer le pour obtenir le troisième des implicant premier de , . Ce que l’étape précédente nous à permis, c’est donc d’obtenir ces fameux implicants premiers (puisqu’on ne peut plus les combiner pour les simplifier).
Deuxième étape
La deuxième étape d’élimination des termes redondants passe par la réalisation d’une table des implicants (ou monômes) premiers.
On réalise un tableau où les entrées des lignes sont composées des termes générateurs, et les entrées des colonnes sont composées des minterms (on élimine cette fois les membres de , puisqu’ils ne sont pas importants). On remplit alors le tableau en indiquant si le terme générateur peut exprimer le minterm. Par exemple, dans le cas de , celui-ci permet d’exprimer 2 et 3 (10 et 11 ne nous intéressent pas).
Dans ce cas, on obtient :
| Termes générateurs | (2) | (3) | (4) | (5) | (6) | (8) | (9) |
|---|---|---|---|---|---|---|---|
| X | X | ||||||
| X | X | ||||||
| X | X | ||||||
| X | X | ||||||
| X | X |
La première chose à faire, c’est de regarder quels sont les termes essentiels, en regardant quelles sont les colonnes dans lesquelles il n’y a qu’une seule croix. Ici, on voit que le terme est le seul permettant d’exprimer 8 et 9, il est donc essentiel. On voit également que 3 ne peut être exprimé que par et que 5 ne peut être exprimé que par , qui sont donc essentiels. Pour les traduire en fonction booléenne, on ne considère que les termes qui ne sont pas , et on a donc , , . Il s’agit bien d’éléments de notre fonction simplifiée obtenue par Karnaugh.
Le « problème », c’est que aucun de ces 3 termes essentiels ne permet d’exprimer 6, pour lequel il faut choisir entre et , dont l’un des deux est redondant. On pourrait choisir au hasard (et tomber dans ce cas-ci sur la bonne réponse quoiqu’il arrive), mais une méthode plus sûre est d’utiliser soit la réduction par domination, soit la méthode de Petrick (en), qui seront expliquées plus bas.
Ici, on peut en fait éliminer n’importe laquelle des deux lignes. Si on élimine la deuxième, on voit qu’on tombe sur , qui est bien le dernier terme manquant à notre fonction simplifiée telle qu’obtenue par Karnaugh. Sinon, on peut éliminer la première ligne, qui permet d’obtenir , qui est également possible. En effet, si on regarde le diagramme de Karnaugh, on voit qu’il y a deux possibilités.
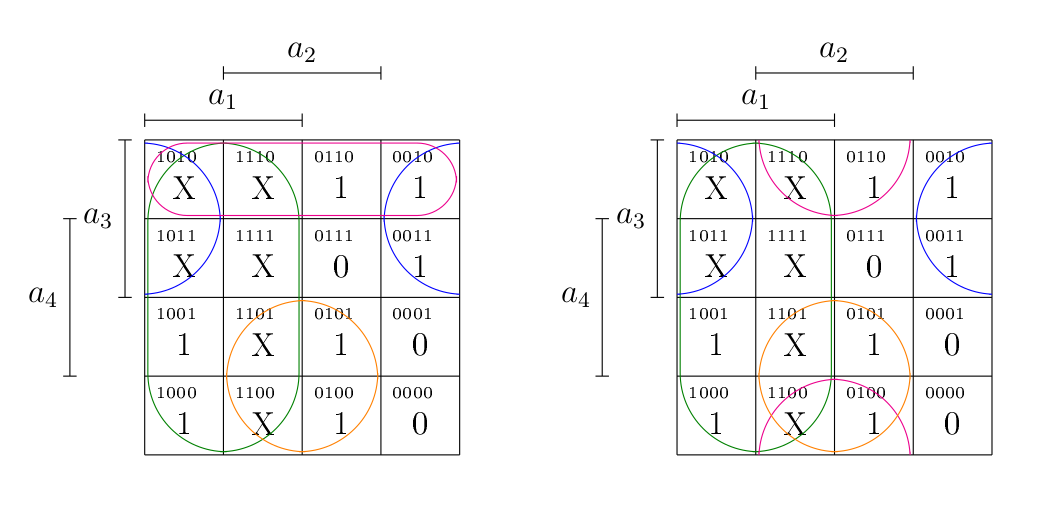
Un autre exemple pour bien comprendre la deuxième étape de l’algorithme
Intéressons-nous maintenant à la fonction suivante (qui n’a probablement pas d’intérêt autre que didactique):
dont je vous épargne la recherche des termes générateurs (en fait ça s’arrête à l’ordre 1) pour vous donner tout de suite la table des implicants premiers.
| Termes générateurs | 0 | 3 | 5 | 6 | 7 | 8 | 9 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|
| X | X | ||||||||
| X | X | ||||||||
| X | X | ||||||||
| X | X | ||||||||
| X | X | ||||||||
| X | X | ||||||||
| X | X | ||||||||
| X | X |
Tout d’abord, on voit que les termes essentiels sont , et , car ils sont les seuls à pouvoir exprimer 0, 3 et 14, respectivement.
On peut obtenir une table réduite en enlevant les termes essentiels et en éliminant les colonnes correspondantes (ainsi que les colonnes pour 6, 7 et 8, qui sont déjà couverts par ces termes essentiels). Ici, on peut également enlever le terme qui n’exprime rien de plus que ces 3 termes essentiels.
| Termes générateurs | 5 | 9 | 13 |
|---|---|---|---|
| X | |||
| X | X | ||
| X | |||
| X | X |
Voyons maintenant comment faire le choix parmi touts ces termes redondants.
Par dominance
La règle de dominance est ainsi énoncée : « une colonne (ou ligne) est dominante relativement à une autre colonne (ou rangée) si elle contient toutes les “x” de l’autre, et au moins un “x” en plus ».
- On peut éliminer une colonne égale ou dominante par rapport à une autre (afin de réduite le nombre de termes).
- On peut éliminer une ligne égale ou dominée par rapport à une autre.
- On extrait alors les nouveaux termes essentiels, puis on recommence si nécessaire.
Ici, aucune colonne n’égale ou ne domine une autre (elles contiennent le même nombre de « X » plus au moins 1). Par contre, on a de la domination dans les lignes : est dominée par et peut donc être éliminée. De même, est dominée par , donc elle disparaît. On obtient alors la table suivante.
| Termes générateurs | 5 | 9 | 13 |
|---|---|---|---|
| X | X | ||
| X | X |
On voit alors que les deux termes restants sont essentiels, puisqu’ils permettent d’exprimer 5 et 9, respectivement. La fonction simplifiée est donc :
Par la méthode de Petrick
- On nomme chaque ligne (chaque terme) de la table des implicants réduite , où est le numéro de la ligne (qui correspond donc à un terme redondant).
- Chaque colonne est représentée par une disjonction (une somme) de ligne.
- La fonction logique totale est représentée par la conjonction (un produit) des lignes.
- On distribue ensuite les termes, et on réduit par le théorème d’absorption (pour rappel, ). On obtient donc une conjonction (une somme) de disjonction (un produit) de lignes.
- On sélectionne les produits avec le moins de littéraux. S’il y a plusieurs possibilités, on pourra alors choisir parmi ceux-ci.
On repart donc de la table simplifiée des implicants premiers, dans laquelle ont été rajoutés les numéros de lignes (étape 1) :
| Termes générateurs | Conjonction | 5 | 9 | 13 |
|---|---|---|---|---|
| X | ||||
| X | X | |||
| X | ||||
| X | X |
On voit que la fonction qu’on obtient (étape 2 et 3) est :
qui exprime simplement que la fonction finale doit être composée de tout les minterms restant (5, 9 et 13), d’où la conjonction, tandis que les disjonctions pour chacun de ceux-ci exprime qu’on peut choisir parmi les termes.
On la simplifie (étape 4) comme suit :
On a donc 3 combinaisons possibles (étape 5) :
- et , qui donnent la somme , soit 5 littéraux différents ( et sont deux littéraux différents) ;
- et , qui donnent la somme , soit 4 littéraux différents ;
- et , qui donnent la somme suivante , soit 5 littéraux différents.
On voit donc bien que c’est et qui doivent être sélectionnées, ce qui était ce qu’on avait obtenu avec la réduction par dominance, et donc la fonction booléenne simplifiée est la même.
Conclusion
Encore une fois, cet algorithme n’est qu’une variation de la méthode de Karnaugh, mais est plus simple à expliquer à un ordinateur afin qu’il simplifie les fonctions booléennes pour nous. Une version encore plus efficace existe ceci dit, nommée Espresso (en), exploitée par le programme du même nom et dont un certain nombre d’implémentations existent.
À nouveau, tout ce travail peut être réalisé en ligne. Parmi le nombre d’implémentations disponibles, je me suis pris d’affection pour celle-ci, qui est une fois encore en anglais et utilise des tirets à la place des , mais qui présente bien chacune des étapes !
- On peut également mettre un tiret à la place du .↩
Dans ce chapitre, on a donc vu que l’algèbre de Boole permettait d’exprimer les mêmes choses que dans le chapitre précédent, mais sous une forme légèrement différente. On a aussi vu, et c’est très important, que ça nous permettait de simplifier ces fonctions logiques. On peut maintenant continuer notre périple pour aller voir comment on peut faire comprendre ça à une machine.
À tout de suite