Retour sur la calculatrice

Nous nous sommes intéressés aux principaux opérateurs arithmétiques à l’exception de l’un d’entre eux : l’opérateur de division (/). Il est un peu différent des autres parce que la division entre deux nombres entiers n’est pas nécessairement un nombre entier.

En effet, que vaut « 5 divisé par 2 » (5 / 2) ? Aucun des nombres que l’on sait représenter n’est égal à ce résultat. Il nous faut aller au-delà des nombres entiers pour découvrir le monde des nombres à virgule, ou nombres flottants. Les nombres flottants se composent d’une partie entière et d’une partie fractionnaire séparées par un point (notation anglaise). Ainsi le résultat de notre précédent calcul se note 2.5.

>>> 5 / 2
2.5

Chaque valeur en Python est associée à un type, c’est-à-dire qu’elle appartient à une certaine catégorie. Cette catégorie régit les opérations qui sont applicables sur ses valeurs. Les nombres entiers (int) et les flottants (float) sont deux types différents, deux catégories distinctes.

>>> 8 / 2
4.0

Ainsi ici Python nous renvoie la valeur 4.0, qui n’est pas la même chose que 4. Les deux valeurs sont égales et représentent le même nombre, mais elles ne sont pas du même type en Python.

Les opérations que nous avons vues sur les nombres entiers s’appliquent aussi aux flottants, la différence étant que le résultat sera toujours un nombre flottant.

>>> 1.1 + 3.4
4.5
>>> 4.5 * 2.7
12.15
>>> 12.15 - 0.1
12.05
>>> 12.05 / 0.5
24.1

Et ces deux types de nombres sont compatibles entre eux, il est par exemple possible d’additionner un entier et un flottant. Là aussi le résultat sera un flottant, pour éviter toute perte d’information de la partie fractionnaire.

>>> 5 + 0.8
5.8
>>> 0.3 * 10
3.0

Une chose à laquelle il faut faire attention avec les nombres à virgule se situe sur les arrondis. Par exemple, il n’est pas possible de représenter la division de 8 par 3 par un nombre à virgule précis, et c’est donc le nombre le plus proche qui nous sera renvoyé par cette opération.

>>> 8 / 3
2.6666666666666665

Mais ça ne s’arrête pas là. Contrairement à nous qui avons l’habitude du système décimal, l’ordinateur stocke les nombres sous forme binaire.
Ainsi, tous les nombres décimaux que nous utilisons ne sont pas représentables par un flottant, et Python devra effectuer un arrondi.

C’est le cas de 0.1 qui est en fait égal à 0.100000000000000005... À l’usage, il est ainsi courant de rencontrer des cas où ces erreurs d’arrondis deviennent visibles, comme dans les exemples suivants.

>>> 0.1 + 0.1 + 0.1
0.30000000000000004
>>> 1.5 * 1.6
2.4000000000000004

Vous trouverez plus d’information sur ces erreurs dans le tutoriel d'@Aabu dédié à l’arithmétique flottante que je vous invite à consulter après ce cours.

L’opérateur de division (/) entre deux nombres calcule une division décimale et renvoie un nombre flottant, mais ce n’est pas la seule opération de division possible.
En effet, Python permet aussi de réaliser une division euclidienne (ou division entière) avec les opérateurs // et %, calculant respectivement le quotient et le reste de la division.

Souvenez-vous : cela correspond à la division posée que l’on apprenait à l’école où à partir du dividende et du diviseur, par multiplications et soustractions successives, on trouvait ce quotient et ce reste (indivisible).

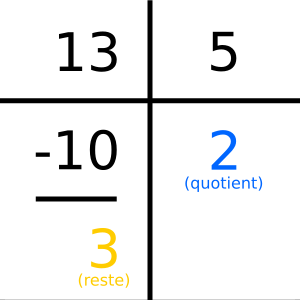
>>> 13 // 5
2
>>> 13 % 5
3

On peut vérifier notre résultat en multipliant le quotient par le diviseur et en lui ajoutant le reste.

>>> 2 * 5 + 3
13

Ces opérations renvoient des nombres entiers quand elles sont appliquées à des nombres entiers.

Une autre opération mathématique courante est l’exponentiation, autrement dit la mise en puissance. Cette opération se note **, avec le nombre à gauche et la puissance à droite.

>>> 5 ** 2 # 5 à la puissance 2 soit 5 au carré
25
>>> 1.5 ** 3 # 1.5 au cube
3.375

Et pour les connaisseurs il est aussi possible d’utiliser des puissances flottantes, comme 0.5 pour calculer une racine carrée.

>>> 2 ** 0.5
1.4142135623730951

Priorités des opérateurs

Comme nous l’avons vu, les opérateurs ont chacun leur priorité, et celle-ci peut être changée à l’aide de parenthèses.
Ainsi, l’exponentiation est prioritaire sur la multiplication et la division, elles-mêmes prioritaires sur l’addition et la soustraction.

Et chaque opérateur a aussi ses propres règles d’associativité. Ce sont des règles qui indiquent si, pour des opérations de même priorité, elles doivent s’exécuter de gauche à droite ou de droite à gauche.

Si elles importent peu pour l’addition et la multiplication ((1+2)+3 et 1+(2+3) ont la même valeur, de même pour (2*3)*4 et 2*(3*4)), elles le sont pour les autres opérations.

Les opérations de priorités 3 et 4 (addition, soustraction, multiplication, divisions) sont toutes associatives à gauche, c’est-à-dire que les opérations de gauche sont exécutées en priorité, de façon à ce que 1 - 2 + 3 soit égal à (1-2) + 3.

>>> 1 - 2 + 3
2
>>> (1 - 2) + 3
2
>>> 1 - (2 + 3)
-4
>>>
>>> 1 / 2 / 3
0.16666666666666666
>>> (1 / 2) / 3
0.16666666666666666
>>> 1 / (2 / 3)
1.5
>>>
>>> 1 / 2 * 3
1.5
>>> (1 / 2) * 3
1.5
>>> 1 / (2 * 3)
0.16666666666666666

À l’inverse, l’opération d’exponentiation (**) est associative à droite, donc les opérations sont exécutées de droite à gauche.

>>> 2 ** 3 ** 4
2417851639229258349412352
>>> 2 ** (3 ** 4)
2417851639229258349412352
>>> (2 ** 3) ** 4
4096

Mais notre calculatrice ne s’arrête pas à ces simples opérateurs, elle est aussi capable d’appliquer des fonctions sur nos nombres. Une fonction est une opération particulière à laquelle on va donner une valeur en entrée et qui va en renvoyer une nouvelle, comme en mathématiques.

Par exemple, abs est la fonction qui calcule la valeur absolue d’un nombre (il s’agit grossièrement de la valeur de ce nombre sans le signe + ou -).
Pour appliquer une fonction sur une valeur, on écrit le nom de la fonction suivi d’une paire de parenthèses, entre lesquelles on place notre valeur.

>>> abs(-5)
5
>>> abs(3.2)
3.2

Faites bien attention aux parenthèses qui sont obligatoires pour appeler une fonction. L’appel sans parenthèses, qui est parfois d’usage en mathématiques ou dans d’autres langages de programmation, produit ici une erreur de syntaxe.

>>> abs 3.2
  File "<stdin>", line 1
    abs 3.2
        ^
SyntaxError: invalid syntax

Une autre fonction sur les nombres fournie par Python est la fonction round qui permet de calculer l’arrondi à l’entier d’un nombre flottant.

>>> round(1.4)
1
>>> round(1.5)
2

Ces deux fonctions abs et round sont prédictibles : pour une même valeur en entrée le résultat sera toujours le même. On pourrait les appeler à l’infini et obtenir toujours la même chose.

Le résultat d’une fonction est donc une valeur comme une autre, ici un nombre, que l’on peut alors utiliser au sein d’autres opérations.

>>> abs(-2) * (round(3.7) - 1)
6

C’est ce que l’on appelle une « expression », cela désigne une ligne de Python qui produit une valeur.
Cela peut être une simple valeur (42), une opération (3 * 5) ou un appel de fonction (abs(-2)) : tous ces exemples sont des expressions, qui peuvent ainsi se composer les unes avec les autres dans de plus grandes expressions.

>>> 42 - 3 * 5 + abs(-2)
29

La valeur que l’on envoie à la fonction est appelée un argument. abs(-5) se lit « appel de la fonction abs avec l’argument -5 », et 5 est la valeur de retour de la fonction.

Un argument est aussi une expression, et l’on peut donc faire un appel de fonction sur une opération et non juste sur une valeur littérale.

>>> abs(3 - 10)
7
>>> round(9 / 2)
4

Les exemples précédents présentaient des appels avec un unique argument. Mais certaines fonctions vont pouvoir recevoir plusieurs arguments, qui devront alors être séparés par des virgules lors de l’appel. Il convient de mettre une espace derrière la virgule pour bien aérer le code.

C’est le cas de la fonction round, qui prend un deuxième argument optionnel permettant de préciser combien de chiffres après la virgule on souhaite conserver. Par défaut, on n’en conserve aucun.

>>> round(2.3456)
2
>>> round(2.3456, 1)
2.3
>>> round(2.3456, 2)
2.35
>>> round(2.3456, 3)
2.346
>>> round(2.3456, 4)
2.3456

D’autres fonctions vont recevoir plusieurs arguments, c’est le cas par exemple de min, qui renvoie la plus petite valeur de ses arguments. À l’inverse, max renvoie la plus grande valeur.

>>> min(4, 9, -2, 7)
-2
>>> max(4, 9, -2, 7)
9

Une fonction est toujours associée à un « ensemble de définition », on ne peut que lui donner des arguments qui sont cohérents avec le calcul qu’elle doit réaliser. abs(1, 2) et min(1) sont par exemple des appels qui n’ont pas de sens et qui produiront des erreurs.

>>> abs(1, 2)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: abs() takes exactly one argument (2 given)
>>> min(1)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'int' object is not iterable

Nous verrons par la suite ce que signifient précisément ces erreurs. Pour l’instant, retenez qu’une fonction attend un certain nombre d’arguments, de certains types. Et que déroger à ces règles produit des erreurs.