Les autres types de données

Les ensembles sont des collections de données pour représenter des valeurs uniques. Dans un ensemble, il ne peut pas y avoir de doublons, un peu comme pour les clés de dictionnaires.

D’ailleurs, la syntaxe pour définir un ensemble ressemble à celle des dictionnaires : un ensemble se définit à l’aide d’accolades à l’intérieur desquelles on sépare les valeurs par des virgules.

>>> {0, 1, 2, 3, 4, 5}
{0, 1, 2, 3, 4, 5}

Si l’on essaie d’insérer des doublons, on voit que ceux-ci ne sont pas pris en compte.

>>> {0, 1, 2, 3, 4, 5, 2, 3}
{0, 1, 2, 3, 4, 5}

Une autre particularité commune aux ensembles et aux dictionnaires est que les valeurs d’un ensemble doivent être hashables, impossible donc d’y stocker des listes.

>>> {[]}
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: unhashable type: 'list'

Il est aussi possible de convertir en ensemble un autre objet en appelant explicitement set (le type des ensembles).

>>> set([0, 1, 2, 3, 4, 5, 2, 3])
{0, 1, 2, 3, 4, 5}

Par ailleurs, {} étant la syntaxe pour définir un dictionnaire vide, un ensemble vide se définit avec set().

>>> set()
set()

Opérations

Les ensembles peuvent être considérés au sens mathématique du terme, une collection contenant juste des valeurs. Et il est ainsi possible d’appliquer des opérations ensemblistes à ces collections.

Ainsi, on peut calculer l’union entre deux ensembles à l’aide de l’opérateur |. L’union de deux ensembles consiste en l’ensemble des valeurs contenues dans l’un ou dans l’autre (ou les deux).

>>> {0, 1, 3, 4} | {2, 3, 4, 5}
{0, 1, 2, 3, 4, 5}

À l’inverse, l’intersection est obtenue avec l’opérateur &. L’intersection ne contient que les valeurs présentes dans les deux ensembles.

>>> {0, 1, 3, 4} & {2, 3, 4, 5}
{3, 4}

La différence est l’opération qui consiste à soustraire au premier ensemble les éléments du second. Elle se calcule avec l’opérateur -.

>>> {0, 1, 3, 4} - {2, 3, 4, 5}
{0, 1}

Enfin, ^ est l’opérateur de différence symétrique. La différence symétrique calcule l’ensemble des valeurs qui ne sont pas communes aux deux ensembles, c’est l’inverse de l’intersection. Ou autrement dit la différence entre l’union et l’intersection.

>>> {0, 1, 3, 4} ^ {2, 3, 4, 5}
{0, 1, 2, 5}
>>> ({0, 1, 3, 4} | {2, 3, 4, 5}) - ({0, 1, 3, 4} & {2, 3, 4, 5})
{0, 1, 2, 5}

J’ai représenté ici les ensembles comme des collections d’éléments ordonnés, mais il n’en est rien, aucune relation d’ordre n’existe dans un ensemble.

Ainsi, deux ensembles sont égaux s’ils contiennent exactement les mêmes valeurs, et différents dans le cas contraire.

>>> {1, 2, 3} == {3, 2, 1}
True
>>> {1, 2, 3} != {2, 3, 4}
True

Il n’y a d’ailleurs pas d’accès direct aux éléments comme il peut y avoir sur une liste, car les éléments ne sont associés à aucun index.
Pour autant, il reste possible de parcourir un ensemble avec une boucle for pour itérer sur ses valeurs.

>>> for i in {1, 2, 3}:
...     print(i)
... 
1
2
3

On peut tester si une valeur est présente dans un ensemble à l’aide de l’opérateur in. Et c’est là tout l’intérêt des ensembles : cette opération est optimisée pour s’exécuter en temps constant (là où il peut être nécessaire de parcourir tous les éléments sur une liste).

>>> 3 in {1, 2, 3}
True
>>> 4 in {1, 2, 3}
False

L’opérateur not in est l’inverse de in, il permet de tester l’absence de valeur.

>>> 3 not in {1, 2, 3}
False
>>> 4 not in {1, 2, 3}
True

Enfin, on trouve d’autres opérations ensemblistes liées aux opérateurs d’égalité.

<, <=, > et >= permettent de tester les sur-ensembles et sous-ensembles.
Avec a et b deux ensembles, a <= b est vraie si tous les éléments de a sont présents dans b (a est un sous-ensemble de b).

>>> {2, 3} <= {1, 2, 3, 4}
True
>>> {2, 3, 5} <= {1, 2, 3, 4}
False

Et l’opération est équivalente à b >= a, vue dans l’autre sens (b est un sur-ensemble de a).

>>> {1, 2, 3, 4} >= {2, 3}
True
>>> {1, 2, 3, 4} >= {2, 3, 5}
False

< et > sont les pendants stricts de ces opérateurs : a < b ne sera pas vraie si a et b contiennent exactement les mêmes valeurs.

>>> {1, 2, 3} < {1, 2, 3, 4}
True
>>> {1, 2, 3} < {1, 2, 3}
False
>>> {1, 2, 3} <= {1, 2, 3}
True

Méthodes

Les ensembles étant des collections, il est naturellement possible d’utiliser la fonction len pour calculer leur taille.

>>> len({1, 2, 3})
3
>>> len({1, 2, 3, 5})
4

Étant modifiables, il est possible d’ajouter et de retirer des éléments dans des ensembles. Cela se fait avec les fonctions add et remove.

>>> values = set()
>>> values.add(2)
>>> values.add(4)
>>> values.add(6)
>>> values
{2, 4, 6}
>>> values.remove(4)
>>> values
{2, 6}

La méthode discard est semblable à remove mais ne lève pas d’erreur si l’élément à supprimer est absent.

>>> values.remove(8)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
KeyError: 8
>>> values.discard(8)
>>> values.discard(2)
>>> values
{6}

Et la méthode pop permet aussi de retirer (et renvoyer) un élément de l’ensemble, sans sélectionner lequel. Elle lève une exception si l’ensemble est vide.

>>> values.pop()
6
>>> values.pop()
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
KeyError: 'pop from an empty set'

On retrouve sinon différentes méthodes sur les ensembles équivalentes aux opérateurs décrits au-dessus : union, intersection, difference et symmetric_difference. L’avantage par rapport aux opérateurs est que ces méthodes peuvent prendre plusieurs ensembles en paramètres, ou même des objets de tous types (itérables) et opérer dessus.

>>> {1, 2}.union({2, 3}, [4], (5, 6))
{1, 2, 3, 4, 5, 6}

Chacune de ces méthodes est doublée d’une version qui modifie en place l’ensemble courant, respectivement update, intersection_update, difference_update et symmetric_difference_update. Ces méthodes ne renvoient rien.

>>> values = {1, 2, 3}
>>> values.intersection_update([3, 4, 5])
>>> values
{3}

Les ensembles disposent aussi de méthodes booléennes, notamment issubset et issuperset équivalentes aux opérateurs <= et >=, ainsi que isdisjoint pour tester si deux ensembles sont disjoints (dont l’intersection est vide).

>>> {1, 2, 3}.isdisjoint({4, 5, 6})
True
>>> {1, 2, 3}.isdisjoint({3, 4, 5})
False

Enfin, on retrouve les méthodes clear et copy, comme sur les listes et les dictionnaires, respectivement pour vider l’ensensemble et pour en faire une copie.

frozenset

Un ensemble étant une collection de données mutable, il n’est pas hashable et ne peut donc pas être utilisé comme clé de dictionnaire. Ainsi, un autre type existe pour représenter un ensemble immutable de données : le frozenset.

Un frozenset se définit en appelant explicitement le type avec n’importe quel itérable en argument.

>>> frozenset({1, 2, 3})
frozenset({1, 2, 3})

Il peut aussi s’appeler seul pour définir un ensemble vide.

>>> frozenset()
frozenset()

Le frozenset dispose des mêmes méthodes et opérateurs que les ensembles classiques, à l’exception de celles qui modifient l’objet.

>>> frozenset({1, 2, 3}) | frozenset({3, 4, 5})
frozenset({1, 2, 3, 4, 5})
>>> frozenset({1, 2, 3}).isdisjoint(frozenset({3, 4, 5}))
False

Les ensembles et les frozenset sont compatibles entre eux, mais attention au type de retour qui dépendra de l’objet sur lequel la méthode ou l’opérateur est appliqué.

>>> frozenset({1, 2, 3}) & {3, 4, 5}
frozenset({3})
>>> {3, 4, 5} & frozenset({1, 2, 3})
{3}

Python dispose encore de nombreux autres types définis dans différents modules de sa bibliothèque standard. Par exemple le module collections propose plusieurs types pour gérer des collections de données avec diverses spécificités.

Counter

Un problème courant en programmation est de vouloir compter des choses. Pour cela, les dictionnaires sont une bonne structure de données : on peut facilement associer un nombre à un élément et ainsi incrémenter ce nombre pour compter les occurrences d’un élément.

>>> numbers = [1, 2, 2, 3, 4, 4, 4]
>>> occurrences = {}
>>> for number in numbers:
...     occurrences[number] = occurrences.get(number, 0) + 1
... 
>>> occurrences
{1: 1, 2: 2, 3: 1, 4: 3}

Il y a en fait beaucoup plus simple avec le type Counter du module collections, spécialement dédié à compter des objets.
Il se comporte comme un dictionnaire où chaque clé non existante serait considérée comme associée à la valeur 0.

>>> from collections import Counter
>>> occurrences = Counter()
>>> occurrences[4]
0
>>> occurrences
Counter()

On peut donc facilement modifier les valeurs sans avoir à se demander si la clé existe déjà.

>>> occurrences[3] += 1
>>> occurrences[5] += 2
>>> occurrences
Counter({5: 2, 3: 1})

Quand une valeur est redéfinie, elle est donc présente « pour de vrai » dans le dictionnaire, même si elle nulle.

>>> occurrences[4] = 0
>>> occurrences
Counter({5: 2, 3: 1, 4: 0})

Un objet Counter peut être initialisé comme un dictionnaire : à partir d’un dictionnaire existant ou à l’aide d’arguments nommés.

>>> Counter({'foo': 3, 'bar': 5})
Counter({'bar': 5, 'foo': 3})
>>> Counter(foo=3, bar=5)
Counter({'bar': 5, 'foo': 3})

Mais il peut aussi être instancié avec un itérable quelconque, auquel cas il s’initialisera en comptant les différentes valeurs de cet itérable.

>>> Counter([1, 2, 3, 4, 3, 1, 3])
Counter({3: 3, 1: 2, 2: 1, 4: 1})
>>> Counter('tortue')
Counter({'t': 2, 'o': 1, 'r': 1, 'u': 1, 'e': 1})

Très pratique donc pour compter directement ce qui nous intéresse.

En plus des opérations communes aux dictionnaires, on trouve aussi des opérations arithmétiques.
Il est ainsi possible d’additionner deux compteurs, ce qui renvoie un nouveau compteur contenant les sommes des valeurs.

>>> Counter(a=5, b=1) + Counter(a=3, c=2)
Counter({'a': 8, 'c': 2, 'b': 1})

À l’inverse, la soustraction entre compteurs renvoie les différences. Les valeurs négatives sont ensuite retirées du résultat.

>>> Counter(a=5, b=1) - Counter(a=3, c=2)
Counter({'a': 2, 'b': 1})

Il est possible de calculer l’union et l’intersection entre deux objets Counter, l’union étant composée des maximums de chaque valeur et l’intersection des minimums (zéro compris).

>>> Counter(a=5, b=1) | Counter(a=3, c=2)
Counter({'a': 5, 'c': 2, 'b': 1})
>>> Counter(a=5, b=1) & Counter(a=3, c=2)
Counter({'a': 3})

Enfin, les compteurs ajoutent quelques méthodes par rapport aux dictionnaires.
most_common par exemple permet d’avoir la liste ordonnée des valeurs les plus communes, associées à leur nombre d’occurrences. La méthode prend un paramètre n pour spécifier le nombre de valeurs que l’on veut obtenir (par défaut toutes les valeurs seront présentes).

>>> count = Counter('abcdabcaba')
>>> count.most_common()
[('a', 4), ('b', 3), ('c', 2), ('d', 1)]
>>> count.most_common(2)
[('a', 4), ('b', 3)]

La méthode elements permet d’itérer sur les valeurs comme si elles étaient représentées plusieurs fois selon leur nombre d’occurrences.

>>> for item in count.elements():
...     print(item)
... 
a
a
a
a
b
b
b
c
c
d

update est une méthode déjà présente sur les dictionnaires, qui a pour effet d’affecter de nouvelles valeurs aux clés existantes. Sur les compteurs, la méthode se chargera de faire la somme des valeurs.
Elle peut prendre n’importe quel itérable en argument, qu’elle considérera comme un compteur.

>>> count.update('bcde')
>>> count
Counter({'a': 4, 'b': 4, 'c': 3, 'd': 2, 'e': 1})

Il est aussi possible de faire la même chose en soustrayant les compteurs avec la méthode substract.

>>> count.subtract('abcd')
>>> count
Counter({'a': 3, 'b': 3, 'c': 2, 'd': 1, 'e': 1})

defaultdict

On a vu il y a quelques chapitres que les dictionnaires possédaient une méthode setdefault. Cette méthode permettait d’assurer qu’une valeur soit toujours présente pour une clé.

Cela simplifie des problèmes où l’on veut associer des listes de valeurs à des clés, comme un annuaire où chaque personne pourrait avoir plusieurs numéros.

>>> phonebook = {}
>>> phonebook.setdefault('Bob', []).append('0663621029')
>>> phonebook.setdefault('Bob', []).append('0714381809')
>>> phonebook.setdefault('Alice', []).append('0633432380')
>>> phonebook
{'Bob': ['0663621029', '0714381809'], 'Alice': ['0633432380']}

Mais les defaultdict permettent cela encore plus facilement : les valeurs manquantes seront automatiquement instanciées, sans besoin d’appel explicite à setdefault. Pour cela, un defaultdict s’instancie avec une fonction (ou un type) qui sera appelée à chaque clé manquante pour obtenir la valeur à affecter.

Ainsi, l’exemple précédent pourrait se réécrire comme suit.

>>> from collections import defaultdict
>>> phonebook = defaultdict(list)
>>> phonebook['Bob'].append('0663621029')
>>> phonebook['Bob'].append('0714381809')
>>> phonebook['Alice'].append('0633432380')
>>> phonebook
defaultdict(<class 'list'>, {'Bob': ['0663621029', '0714381809'], 'Alice': ['0633432380']})

Chaque fois qu’une clé n’existe pas dans le dictionnaire, defaultdict fait appel à list qui renvoie une nouvelle liste vide.

Il suffit d’ailleurs d’essayer d’accéder à la valeur associée à une telle clé pour provoquer sa création.

>>> phonebook['Alex']
[]
>>> phonebook
defaultdict(<class 'list'>, {'Bob': ['0663621029', '0714381809'], 'Alice': ['0633432380'], 'Alex': []})

Et bien sûr, toute fonction pourrait être utilisée comme argument à defaultdict.

>>> def get_default_color():
...     return 'noir'
... 
>>> colors = defaultdict(get_default_color)
>>> colors['mur'] = 'bleu'
>>> colors['mur']
'bleu'
>>> colors['sol']
'noir'

OrderedDict

Avant Python 3.6 les dictionnaires ne conservaient pas l’ordre d’insertion des clés. La seule manière d’avoir un dictionnaire ordonné était d’utiliser le type OrderedDict du module collections. Les choses ont évolué depuis et le type a un peu perdu de son intérêt.

Comme les dictionnaires, un OrderedDict se construit à partir d’un dictionnaire existant et/ou d’arguments nommés. Sans argument, on construit simplement un dictionnaire vide.

>>> from collections import OrderedDict
>>> OrderedDict()
OrderedDict()
>>> OrderedDict({'foo': 0, 'bar': 1})
OrderedDict([('foo', 0), ('bar', 1)])
>>> OrderedDict(foo=0, bar=1)
OrderedDict([('foo', 0), ('bar', 1)])

On le voit par sa représentation, le dictionnaire ordonné est en fait vu comme une liste de couples clé/valeur.

Il reste néanmoins une différence importante entre les dictionnaires ordonnés et les dictionnaires standards : l’ordre des éléments fait partie de la sémantique du premier.

Là où deux dictionnaires seront considérés comme égaux s’ils ont les mêmes couples clé/valeur, quel que soit leur ordre, ça ne sera pas le cas pour les OrderedDict qui ne seront égaux que si leurs clés sont dans le même ordre.

>>> {'foo': 0, 'bar': 1} == {'bar': 1, 'foo': 0}
True
>>> OrderedDict(foo=0, bar=1) == OrderedDict(bar=1, foo=0)
False
>>> OrderedDict(foo=0, bar=1) == OrderedDict(foo=0, bar=1)
True

Ce n’est bien sûr valable que pour l’égalité entre deux dictionnaires ordonnés. L’égalité entre un dictionnaire ordonné et un standard ne tiendra pas compte de l’ordre.

>>> OrderedDict(foo=0, bar=1) == {'bar': 1, 'foo': 0}
True

Faites donc appel à OrderedDict si vous avez besoin d’un tel comportement, sinon vous pouvez vous contenter d’un dictionnaire standard.

ChainMap

Parfois on a plusieurs dictionnaires que l’on aimerait pouvoir considérer comme un seul, sans pour autant nécessiter de copie vers un nouveau dictionnaire qui les intégrerait tous. En effet, la copie peut être coûteuse et elle n’a surtout lieu qu’une fois, le dictionnaire copié ne sera pas affecté si les dictionnaires initiaux sont modifiés.

>>> phonebook_sim = {'Alice': '0633432380', 'Bob': '0663621029'}
>>> phonebook_tel = {'Alex': '0714381809'}
>>> phonebook = dict(phonebook_sim) # Copie pour fusionner les deux dictionnaires
>>> phonebook.update(phonebook_tel)
>>> phonebook
{'Alice': '0633432380', 'Bob': '0663621029', 'Alex': '0714381809'}
>>> phonebook_tel['Mehdi'] = '0762253973'
>>> phonebook # phonebook n'a pas changé
{'Alice': '0633432380', 'Bob': '0663621029', 'Alex': '0714381809'}

Le type ChainMap répond à ce problème puisqu’il permet de chaîner des dictionnaires dans un seul tout.

>>> from collections import ChainMap
>>> phonebook_sim = {'Alice': '0633432380', 'Bob': '0663621029'}
>>> phonebook_tel = {'Alex': '0714381809'}
>>> phonebook = ChainMap(phonebook_sim, phonebook_tel)
>>> phonebook
ChainMap({'Alice': '0633432380', 'Bob': '0663621029'}, {'Alex': '0714381809'})

Lors de la recherche d’une clé, les dictionnaires seront parcourus successivement pour trouver la valeur.

>>> phonebook['Bob']
'0663621029'
>>> phonebook['Alex']
'0714381809'

Si la clé n’existe dans aucun dictionnaire, on obtient une erreur KeyError comme habituellement.

>>> phonebook['Mehdi']
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/usr/lib/python3.8/collections/__init__.py", line 891, in __getitem__
    return self.__missing__(key)            # support subclasses that define __missing__
  File "/usr/lib/python3.8/collections/__init__.py", line 883, in __missing__
    raise KeyError(key)
KeyError: 'Mehdi'

L’objet ChainMap ne contient que des références vers nos dictionnaires, et donc reflète bien les modifications sur ces derniers.

>>> phonebook_tel['Mehdi'] = '0762253973'
>>> phonebook['Mehdi']
'0762253973'

Aussi, il est possible de directement affecter des valeurs au ChainMap, celles-ci seront affectées au premier dictionnaire de la chaîne.

>>> phonebook['Julie'] = '0619096810'
>>> phonebook_sim
{'Alice': '0633432380', 'Bob': '0663621029', 'Julie': '0619096810'}

Il en est de même pour les clés qui existeraient dans les dictionnaires suivants, elles seraient tout de même assignées au premier (c’est le seul accessible en écriture).

>>> phonebook['Alex'] = '0734593960'
>>> phonebook
ChainMap({'Alice': '0633432380', 'Bob': '0663621029', 'Julie': '0619096810', 'Alex': '0734593960'}, {'Alex': '0714381809', 'Mehdi': '0762253973'})

On voit ainsi comment se passe la priorité entre les dictionnaires en lecture : la chaîne est parcourue et s’arrête au premier dictionnaire contenant la clé.

>>> phonebook['Alex']
'0734593960'

Cette fonctionnalité est très pratique pour mettre en place des espaces de noms, comme les scopes des fonctions en Python : des variables existent à l’intérieur de la fonction et sont prioritaires par rapport aux variables extérieures.

La méthode new_child et l’attribut parents sont utiles pour cela puisqu’ils permettent respectivement d’ajouter un nouveau dictionnaire en tête de la chaîne (qui comprendra donc toutes les futures modifications sur le ChainMap) et de récupérer la suite de la chaîne (la chaîne formée par tous les dictionnaires sauf le premier).

Tous deux renvoient un nouvel objet ChainMap sans altérer la chaîne courante.

>>> new_phonebook = phonebook.new_child()
>>> new_phonebook['Max'] = '0704779572'
>>> new_phonebook
ChainMap({'Max': '0704779572'}, {'Alice': '0633432380', 'Bob': '0663621029', 'Julie': '0619096810', 'Alex': '0734593960'}, {'Alex': '0714381809', 'Mehdi': '0762253973'})
>>> new_phonebook.parents
ChainMap({'Alice': '0633432380', 'Bob': '0663621029', 'Julie': '0619096810', 'Alex': '0734593960'}, {'Alex': '0714381809', 'Mehdi': '0762253973'})

new_child peut s’utiliser sans argument, auquel cas un dictionnaire vide sera ajouté, ou en donnant directement le dictionnaire à ajouter en argument.

>>> phonebook.new_child({'Max': '0704779572'})
ChainMap({'Max': '0704779572'}, {'Alice': '0633432380', 'Bob': '0663621029', 'Julie': '0619096810', 'Alex': '0734593960'}, {'Alex': '0714381809', 'Mehdi': '0762253973'})

On retrouve sinon les mêmes méthodes que sur les dictionnaires.

deque

En Python les tableaux sont trompeusement appelés des listes là où ce terme fait souvent référence à des listes chaînées. Un tableau représente des données contigües en mémoire, qui ne peuvent pas être morcellées, et occupe donc une zone mémoire continue qui dépend de sa taille.

Ainsi, lorsque l’on ajoute ou retire des éléments à un tableau, il peut être nécessaire d’adapter la taille de la zone mémoire, voire d’en trouver une nouvelle plus grande et d’y copier tous les éléments. Python fait cela pour nous, mais ce sont des opérations qui peuvent s’avérer coûteuses.

Les listes chaînées à l’inverse sont des chaînes constituées de maillons, chaque maillon étant un élément avec son propre espace mémoire, ceux-ci peuvent être n’importe où dans la mémoire.
L’idée est que chaque maillon référence le précédent et/ou le suivant dans la chaîne.

On pourrait par exemple voir un maillon comme un dictionnaire avec 2 clés : next pour référencer le maillon suivant et value pour la valeur contenue (car l’idée est quand même bien d’y stocker des valeurs).

Voici ainsi un équivalent en liste chaînée de la liste [1, 2, 3, 4].

>>> node4 = {'next': None, 'value': 4}
>>> node3 = {'next': node4, 'value': 3}
>>> node2 = {'next': node3, 'value': 2}
>>> node1 = {'next': node2, 'value': 1}
>>> values = node1

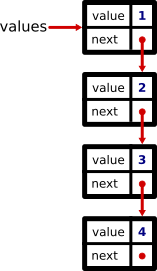
Les variables node1, node2 etc. ne sont que temporaires pour la création de notre liste, elles n’existent plus après, seule values référence notre chaîne de maillons.

>>> del node1
>>> del node2
>>> del node3
>>> del node4

Il nous serait alors possible d’itérer sur notre liste chaînée pour accéder à chacune des valeurs.

>>> node = values # La liste représente le premier maillon
>>> while node is not None: # None représente la fin de liste
...     print(node['value'])
...     node = node['next'] # On passe au nœud suivant en réaffectant node
... 
1
2
3
4

Mais il n’est pas question ici de recoder une liste chaînée, Python en propose déjà une avec le type deque du module collections.
deque pour double-end queue, c’est-à-dire une queue (liste chaînée) dont les deux extrémités sont connues (le premier et le dernier maillon) et les liaisons sont doubles (chaque maillon référence le précédent et le suivant), contrairement à notre implémentation où seul le premier maillon était connu et les liaisons étaient simples (référence vers le maillon suivant uniquement).

Le principe est sinon le même. Un deque se construit comme une liste, soit vide soit à partir d’un itérable existant.

>>> deque()
deque([])
>>> deque([1, 2, 3, 4])
deque([1, 2, 3, 4])

Et le type propose les mêmes méthodes que les listes, ce sont juste les algorithmes derrière qui sont différents, et certaines opérations qui sont à privilégier plutôt que d’autres.

>>> values = deque([1, 2, 3, 4])
>>> values[0]
1
>>> values.append(5)
>>> values
deque([1, 2, 3, 4, 5])

Par exemple, contrairement aux tableaux (list) il est très facile (peu coûteux) d’ajouter des éléments au début ou à la fin, puisqu’il suffit d’insérer un nouveau maillon à l’extrémité et de changer la référence. De même pour supprimer un élément au début ou à la fin.

Les deque proposent d’ailleurs des méthodes dédiées avec appendleft et popleft, équivalentes à append et pop mais pour opérer au début de la liste.

>>> values.appendleft(0)
>>> values
deque([0, 1, 2, 3, 4, 5])
>>> values.popleft()
0
>>> values
deque([1, 2, 3, 4, 5])

En revanche, comme seules les extrémités sont connues, il est coûteux d’aller chercher un élément en milieu de liste, puisqu’il est nécessaire pour cette opération de parcourir tous les maillons jusqu’au bon élément.

>>> values[2]
3

Pour accéder à cette valeur, il a fallu parcourir 3 maillons. Il aurait fallu en parcourir 500 pour atteindre le milieu d’une liste chaînée de 1000 éléments. Là où pour un tableau l’accès à chaque élément est direct puisque son emplacement mémoire est connu : il se calcule facilement à partir de la position du premier élément, les éléments étant contigüs en mémoire.

Ainsi, ne faites appel aux listes chaînées que pour des opérations qui nécessiteraient de souvent ajouter et/ou supprimer des données en début/fin de séquence, c’est là leur intérêt par rapport aux tableaux.
Ne les utilisez pas si vous devez accéder régulièrement à des éléments situés loin des extrémités, les performances pourraient être désastreuses.

namedtuple

Pour terminer avec le module collections, j’aimerais vous parler des named tuples (tuples nommés).

Vous le savez, un tuple représente un ensemble cohérent de données, par exemple deux coordonnées qui identifient un point dans le plan. Il est sinon semblable à une liste (bien que non modifiable) et permet d’accéder aux éléments à partir de leur position.

>>> point = (3, 5)
>>> point[0]
3

Et par unpacking il est possible d’accéder à ses éléments indépendemment.

>>> x, y = point
>>> y
5

Mais ne serait-il pas plus pratique de pouvoir directement taper point.y pour accéder à l’ordonnée du point ? C’est plus facilement compréhensible que point[1] et moins contraignant que l'unpacking qui nécessite de définir une nouvelle variable.

Vous le voyez venir, c’est ce que proposent les tuples nommés : donner des noms aux éléments d’un tuple. Mais tout d’abord, il faut créer un type associé à ces tuples nommés, pour définir justement les noms de champs. Car un tuple nommé identifiant un point ne sera pas la même chose qu’un tuple nommé identifiant une couleur par exemple.

Nous allons donc devoir définir un nouveau type et c’est précisément ce que fait la fonction namedtuple du module collections : elle crée dynamiquement un type de tuples nommés en fonction des arguments qu’elle reçoit. Pour ça, elle prend en arguments le nom du type à créer (utilisé pour la représentation de l’objet) et la liste des noms des champs des tuples.

La fonction renvoie un type, mais il faudra assigner ce retour à une variable pour pouvoir l’utiliser, comme tout autre retour de fonction. Les types en Python sont en fait des objets comme les autres, qui peuvent donc être assignés à des variables. Par convention, on utilisera un nom commençant par une majuscule, pour identifier un type.

>>> from collections import namedtuple
>>> Point = namedtuple('Point', ('x', 'y'))
>>> Point
<class '__main__.Point'>

Ensuite, pour instancier un objet Point, on appelle le type en lui donnant en arguments les deux coordonnées x et y.

>>> point = Point(3, 5)
>>> point
Point(x=3, y=5)
>>> point.x
3

On le voit à sa représentation, il est aussi possible d’instancier l’objet en utilisant des arguments nommés.

>>> Point(x=10, y=7)
Point(x=10, y=7)

Notre objet point est toujours un tuple, et il reste possible de l’utiliser comme tel.

>>> point[0]
3
>>> x, y = point
>>> y
5

Nous avons maintenant vu de nombreux types Python, mais savons-nous reconnaître les valeurs d’un certain type ? Oui, à l’usage on sait différencier une chaîne de caractères d’un nombre, parce qu’ils se représentent différemment, et qu’on y applique des opérations différentes.
Mais il est possible d’aller plus loin dans la reconnaissance des types et nous allons voir quels outils sont mis à disposition par Python pour cela.

Premièrement, la fonction type¹ permet de connaître le type d’un objet. On lui donne une valeur en argument et la fonction nous renvoie simplement son type.

>>> type(5)
<class 'int'>
>>> type('foo')
<class 'str'>
>>> type([0])
<class 'list'>

Cela peut être utile dans des phases de débogage, pour s’assurer qu’une valeur est bien du type auquel on pense.
On peut aussi l’utiliser dans le code pour vérifier le type d’un objet mais ce n’est généralement pas recommandé (car trop strict, voir plus bas).

>>> def check_type(value):
...     if type(value) is str:
...         print("C'est une chaîne de caractères")
...     else:
...         print("Ce n'est pas une chaîne de caractères")
... 
>>> check_type('foo')
C'est une chaîne de caractères
>>> check_type(5)
Ce n'est pas une chaîne de caractères

L’autre outil mis à disposition de Python pour reconnaître le type d’une valeur est la fonction isinstance. Cette fonction reçoit une valeur et un type, et renvoie un booléen selon que la valeur soit de ce type ou non.

>>> isinstance('foo', str)
True
>>> isinstance(5, str)
False

Mais une valeur n’est pas d’un seul type, il existe en fait une hiérarchie entre les types. Par exemple, tous les objets Python sont des instances du type object, car object est le parent de tous les types.

>>> isinstance('foo', object)
True
>>> isinstance(5, object)
True

Ou encore, avec notre objet point construit précédemment, qui est à la fois une instance de Point et de tuple.

>>> type(point)
<class '__main__.Point'>
>>> isinstance(point, Point)
True
>>> isinstance(point, tuple)
True

Cela nous montre une première limitation de l’appel à type pour vérifier le type, qui ne verrait pas que nos valeurs sont aussi des object, ou notre point un tuple.

>>> type('foo') is object
False
>>> type(5) is object
False
>>> type(point) is tuple
False

Vérifier avec type est donc à limiter aux cas où l’on veut s’assurer strictement du type d’un objet, sans considérer la hiérarchie des types, et ce sont des cas assez rares.

Il faut cependant faire attention aussi aux appels à isinstance et les utiliser avec parcimonie, au risque de contrevenir à une caractéristique importante du Python, le duck-typing.

Ainsi, on évitera les if isinstance(value, list): ... si ce n’est pas strictement nécessaire (un traitement particulier à réserver aux objets de ce type), pour ne pas laisser de côté les autres types qui auraient pu convenir tels que les tuples.

Mais isinstance ne se limite pas à des types clairement définis et permet aussi de vérifier des interfaces. C’est ce que propose le module collections.abc qui fournit une collection de types abstraits (abc pour abstract base classes, classes mères abstraites), des interfaces correspondant à des comportements en particulier.

On trouve ainsi un type Iterable. Il n’est pas utilisable en tant que tel, on ne peut pas instancier d’objets du type Iterable, mais on peut l’utiliser pour vérifier qu’un objet est bien itérable en appelant isinstance.

>>> from collections.abc import Iterable
>>> isinstance([1, 2, 3], Iterable)
True
>>> isinstance((4, 5, 6), Iterable)
True
>>> isinstance('hello', Iterable)
True
>>> isinstance(42, Iterable)
False

Il y a aussi Hashable par exemple pour vérifier qu’une valeur est hashable, que l’on peut l’utiliser en tant que clé dans un dictionnaire ou la stocker dans un ensemble.

>>> from collections.abc import Hashable
>>> isinstance(42, Hashable)
True
>>> isinstance('hello', Hashable)
True
>>> isinstance([1, 2, 3], Hashable)
False
>>> isinstance((4, 5, 6), Hashable)
True

On trouve encore d’autres types abstraits définis dans collections.abc mais il est un peu tôt pour les aborder.