L’île de Zeest 1 est une petite île2 de 1000 âmes, située au large du continent européen. Il s’agit d’un endroit tranquille et un peu reculé, car le seul moyen d’y parvenir est bien entendu par bateau, qui part le matin et revient le soir. Il s’agit donc d’un endroit où on prend le temps, peuplé principalement de retraités qui jouissent de leur retraite dûment obtenue. On aime s’y promener, discuter avec ses voisins de tout et de rien, aller au marché, taper la carte, supporter l’équipe locale de pétanque qui s’entraîne pour le championnat régional, etc. Bref, un petit bout de terre très convoité, où les places sont rares : la liste d’attente de l’unique agence immobilière de l’île compte plus de 300 envieux.
Mais voilà : depuis quelques semaines, une nouvelle maladie3 frappe le continent : la violite. Elle tire son nom du teint qu’elle donne aux personnes infectées, car elle s’attaque aux globules rouges pour en changer la couleur, ce qui s’accompagne évidemment d’une diminution du transport d’oxygène et de tous les désagréments qui vont avec. Heureusement, la maladie n’est pas mortelle si elle est prise en charge à temps. Néanmoins, la situation inquiète le maire de l’île, André Gérard, vu la forme de coupe que forme la pyramide des âges de ses administrés et leur santé parfois vacillante : il ne faudrait pas que les habitants se mettent à tomber comme des mouches. Après avoir commandé son contingent de pyrrozine4, un anti-pelliculaire reconverti et seul remède connu contre la violite, le maire passe un coup de fil à sa fille, Louise, mathématicienne et à son frère, Guy, informaticien. À trois, leur but va être de prédire et de comprendre les effets qu’une éventuelle épidémie pourrait avoir afin de prendre les mesures qui s’imposent.
Ce que je vais faire dans cet article n’a aucun pouvoir prédictif (d’autant que le modèle employé est très simple) : il y a des gens qui font ça bien mieux que moi avec des données réelles, ce qui ne sera pas le but ici
Vous l’aurez compris, on va parler d’épidémie, de et d’immunité de groupe. Et, à côté du role play, on va faire un peu de maths pour bien comprendre
Dans ce tutoriel, pour les parties plus mathématiques d’interprétation, je vais partir du principe que vous n’êtes pas étranger aux notions de statistiques (simples) et que vous connaissez le principe de dérivée et d’intégration (et éventuellement d’équation différentielle).
- Approche stochastique : simuler et constater
- Approche déterministe : modéliser et comprendre
- Au delà du modèle SIR
Approche stochastique : simuler et constater
On va donc tenter de simuler une épidémie.
Évidemment, les résultats vont dépendre de la manière dont cette simulation va avoir lieu, mais on va essayer de coller à une réalité épidémique. On va débuter en utilisant le modèle SIR qui est le modèle de base en épidémiologie, car il s’applique sous hypothèses plus ou moins fortes à plein de cas différents.
Le modèle Susceptible-Infecté-Guéri (SIR)
On va commencer par distinguer 3 stades de la maladie :
- Susceptible () : la personne n’a pas encore été infectée par la maladie.
- Infecté () : la personne est atteinte de la maladie. Partons du principe que dans cet état, elle est également contagieuse et peut donc infecter d’autres personnes susceptibles. Du coup, on part ici du principe que la personne continue à avoir des contacts avec l’extérieur même si elle est malade.
- Guéri (, pour recovered en anglais) : la personne n’est plus malade et n’est plus contagieuse. On va également partir du principe qu’elle est immunisée à vie.
On verra qu’on peut ensuite complexifier quasiment à l’envi cette situation.
Notons qu’une personne ne peut pas appartenir à plusieurs catégories à la fois : il s’agit en effet d’un modèle compartimental, où chaque individu est dans un compartiment donné et peut évoluer pour passer dans un autre compartiment, ici dans le sens . Si on note le pourcentage d’individus dans le compartiment au temps , on a (avec ) que
Et on espère évidemment que , autrement dit que l’épidémie s’arrête.
On va également partir du principe que le passage d’un compartiment à un autre est purement statistique : par exemple un individu infecté a une certaine probabilité, qu’on va noter , d’infecter un autre individu qui ne l’est pas encore. À l’échelle macroscopique, c’est relativement réaliste : plus qu’une probabilité d’infecter, il faut voir ça comme le fait que les personnes auront plus ou moins de contacts avec l’extérieur durant le temps où elles sont contagieuses1. De même, la probabilité de guérison, qu’on va noter , modélise simplement le fait que certains sont malades plus longtemps que d’autres. On reprend généralement tout ceci dans un schéma de la sorte :

À l’échelle d’une personne donnée, la probabilité d’infection et de guérison suivent toutes deux une loi géométrique. Soit la probabilité de passer d’un compartiment à un autre et le nombre d’essais (rencontre d’une personne infectée pour la transition ou temps qui passe pour la transition ), la probabilité d’y parvenir à la ième tentative est donnée par
c’est-à-dire la probabilité de échecs, suivie de la probabilité d’un succès. C’est cette même loi qui modélise la probabilité que vous fassiez un 3 au dé si c’est la quatrième fois que vous essayez. Notez qu’en moyenne2, le nombre de tentatives nécessaires est donné par
Ici, est donc aussi bien le nombre de personnes infectées rencontrées () que le nombre d’unités de temps passée à être malade (). Et donc, si le taux d’infection est de = 20%, alors une personne susceptible finira infectée en moyenne au bout de = 5 contacts, et si le taux de guérison est de = 10%, alors la personne sera guérie en moyenne au bout de = 10 unités de temps.
La simulation
Bien entendu, mettre toute l’île en quarantaine préventive est irréaliste : la plupart des produits viennent par bateau et, vu que l’île ne possède pas d’hôpital, plusieurs résidents doivent retourner régulièrement sur le continent, sans compter les quelques personnes qui font le voyage tous les jours pour y travailler. Le but est donc d’imaginer ce qu’il se passerait si, par malheur, quelqu’un ramenait la maladie sur l’île. Pour Guy, il s’agira de fournir une petite simulation pour aider son frère à bien comprendre l’impact de ses futurs choix, en particulier en matière de confinement. Guy veut donc faire vite et bien, car la contagion peut survenir à n’importe quel moment. En soit, rien de compliqué : c’est comme si, dans un jeu, on lançait un dé pour déterminer si une personne est infectée ou guérie. Et en informatique, on peut lancer énormément de dés…
Le principe est inspiré de cet article de blog (traduit de celui-ci, en anglais) qui présente et discute plein de manières de modifier une simulation et des effets des différents paramètres.
En pratique, j’ai choisi de prendre une population disposée sur une grille. On débute avec une poignée, , de personnes infectées distribuées au hasard sur la grille et on considère un intervalle de temps discret : à chaque étape de la simulation, on calcule ce qui s’est passé entre l’unité de temps précédente et celle-ci, de manière purement aléatoire. C’est un processus stochastique.
Durant une unité de temps, une personne infectée fait rencontres et peut potentiellement infecter les personnes rencontrées ( étant un paramètre que vous pouvez modifier durant la situation). Dès lors, si on part du principe qu’une personne infectée l’est en moyenne durant unités de temps, on en déduit qu’une personne infectée rencontre en moyenne personnes durant ce laps de temps.
En pratique, on passe en revue la liste des personnes infectées :
- On vérifie tout d’abord que la personne infectée n’est pas guérie en tirant un premier nombre aléatoire . Elle est guérie si .
- Si elle ne l’est pas, elle rencontre au hasard personnes. Si la personne rencontrée est susceptible, on tire un second nombre aléatoire , qui infecte la personne si .
Afin de simuler l’effet de mesures de confinement, j’ai choisi de rajouter un autre paramètre : les rencontres que fait une personne infectée ne peuvent se faire que dans un certain rayon , autour de la personne infectée, ce qui donne tout son intérêt à la grille : une personne ne peut infecter que ses voisins proches. Pour me simplifier la vie, c’est la distance dite de Manhattan qui est considérée ici : sur une grille, c’est maximum 4 personnes pour un rayon de 1, 12 pour un rayon de 2, etc :
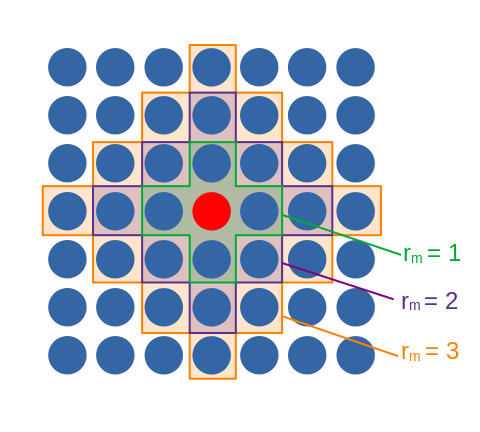
La simulation se termine lorsque plus personne ne peut être infecté. Cela signifie que des gens peuvent très bien ne jamais avoir contracté la maladie : la valeur de mesure donc le nombre de personnes qui n’ont jamais été malades.
Par défaut, j’utilise les paramètres suivants, dont on va dire qu’ils sont réalistes dans la situation qui nous occupe3 :
- = 1%.
- = 20%, = 10% : on est en moyenne contaminé au bout de 5 contacts avec une personne infectée et la maladie dure à peu près 10 unités de temps.
- = 4 et = 3. Autrement dit, une personne infectée fait 4 rencontres par unité de temps, parmi, au maximum, 24 personnes : évidemment sur les côtés de la grille, il y a des effets de bord qui réduisent le nombre de possibilités. En moyenne, une personne infectieuse fait donc 40 rencontres, que les personnes infectées soient elle-mêmes infectées ou pas.
La simulation se présente en trois parties : la première est constituée de sliders, vous permettant d’ajuster les différents paramètres. Des boutons vous permettent ensuite de lancer la simulation (et de la mettre en pause), ou d’avancer d’une seule unité de temps. La seconde partie est une visualisation des personnes : en bleu pour les personnes susceptibles, en rouge pour les personnes infectées et en vert pour les personnes guéries. Finalement, la troisième partie est un graphique reprenant l’évolution des trois populations au cours du temps.
Vous pouvez jouer avec la simulation ici :
Plusieurs reproches peuvent être faits à cette simulation. Je vais les énoncer tout de suite pour qu’on puisse se concentrer sur les résultats :
- Je me repose sur le générateur de nombres aléatoires par défaut,
Math.random(), sans savoir ce qu’il y a derrière (il dépend du navigateur). Pour faire de vraies simulations, il vaut mieux utiliser des générateurs dont on sait qu’ils se comportent bien, comme par exemple le Mersenne Twister (non, ce n’est pas une variante chelou du Twister).
- L’utilisation d’une grille est discutable : on pourrait utiliser des réseaux, modélisant le nombre d’interactions qu’un individu peut avoir. Évidemment, ça reporte le problème sur l’obtention de tels réseaux pour être réaliste, mais ça permet de faire de chouettes choses, comme faire apparaître la fameuse notion de cluster.
- Au niveau de l’implémentation, on peut faire un peu mieux en utilisant l'algorithme de Gillepsie, justement fait pour ce genre de cas où on modélise en fait des chaînes de Markov, c’est-à-dire que l’étape suivante dépend seulement de l’état précédent. D’ailleurs, on va utiliser des éléments de cette théorie par la suite.
Bref, comme toute modélisation, ça permet d’obtenir des résultats dans les limites qu’on s’est fixées. Si vous ne deviez retenir qu’un seul message de cet article, c’est celui-là.
Les résultats
Vu que c’est de l’aléatoire, il faut lancer plusieurs fois la simulation et faire une moyenne pour obtenir des tendances correctes (ce que j’ai fait ). Lorsque je présenterai un graphe issu de la simulation, ne vous focalisez pas sur les chiffres, mais plutôt sur la tendance qui s’en dégage.
Avec les paramètres par défaut
Voici un exemple de résultat obtenu avec les paramètres par défaut :
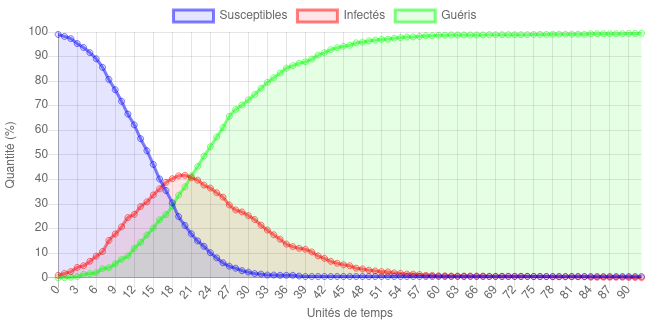
Qu’est ce qu’on peut noter ?
- Le nombre de personnes infectées croit très vite et présente un maximum aux alentours de 20 unités de temps, avec 40% de la population infectée en même temps (pour environ 30% de personnes susceptibles et 30% de personnes déjà guéries). Notez qu’en faisant la différence entre deux points successifs de la courbe des personnes susceptibles, on peut calculer que le nombre de personnes nouvellement infectées se situe entre 3 et 4% à ce moment de l’épidémie.
- Le nombre de personnes infectées décroît ensuite lentement et la maladie finit par disparaître après environ 100 unités de temps. Tout le monde (ou presque) y passe : à la fin de la simulation, le nombre de personnes guéries est de presque 100%.
Évidemment, ces deux points sont problématiques : d’une part parce qu’on risque d’atteindre très vite la saturation des services de santé qui doivent traiter toutes ces nouvelles personnes infectées, d’autre part parce qu’exposer toute la population à la maladie augmente le nombre de personnes présentant des complications, que lesdits services devront également traiter.
Notez qu’on peut, sous hypothèses, facilement estimer la probabilité qu’une personne infectée en contamine à elle seule autres durant le temps ou elle est infectée en utilisant la loi binomiale négative. En partant du principe que la personne infectée ne rencontre que des personnes susceptibles, on calcule en fait la probabilité d’infecter personnes et de ne pas en infecter (pour un total de recontres), l’infection ayant une probabilité d’arriver. La formule est
où je vais utiliser la notation pour la probabilité d’obtenir succès et échecs ( est la variable aléatoire qu’on cherche à calculer). est le coefficient binomial.
Par ailleurs si on veut calculer la probabilité pour que les infections se fasse avec au plus échecs, on doit sommer toutes les probabilités de à (puisqu’il s’agit de la probabilité d’obtenir les infections avec 0 échecs, 1 échec, 2 échecs, etc):
Pour = 20% et en imaginant qu’une personne infectieuse fait, comme expliqué plus haut, = 40 rencontres de personnes susceptibles, la probabilité d’en infecter 5 (=5, =35) est de 92%. Elle tombe à 27% pour la probabilité d’infecter 10 personnes (=10, =30) et est inférieure à 1% d’infecter au moins 15 personnes (=15, =25).4
Bien entendu, en réalité, une personne infectée peut ensuite en infecter une autre, donc les infections se cumulent
Jouer avec les paramètres
À la vue de ses résultats, André se rend très bien compte que si rien n’est fait, le pire est à venir : l’île compte 3 médecins5, qui devraient donc traiter plusieurs dizaines de nouveaux patients par jour au début de l’épidémie. C’est sans compter l’impact sur la vie de l’île, avec toutes les fermetures dues à d’éventuels repos maladie. Pour essayer de contenir l’épidémie au mieux, André peut donc tenter d’en mesurer l’impact en déplaçant les différents curseurs. Bien entendu, il n’a aucun contrôle sur le taux de guérison, à moins qu’un nouveau médicament ne soit mis sur le marché. Mais les autres ?
Premièrement, le nombre de personnes initialement infectées ne change pas grand-chose : même avec = 0,1% (c’est-à-dire une personne sur 1000 !), les nombres évoluent de manière similaire, juste que l’épidémie survient un tout petit peu plus tard et est un peu plus longue6. Si vous avez essayé plusieurs fois, vous avez ceci dit constaté qu’il existe un cas où l’épidémie s’arrête : lorsque le premier patient infecté guérit à la première étape de la simulation, n’ayant eu le temps d’infecter personne. Si vous suivez bien, cela arrive… une fois sur 10 à peu près.
Réduire le rayon de rencontre rend déjà la chose plus supportable :
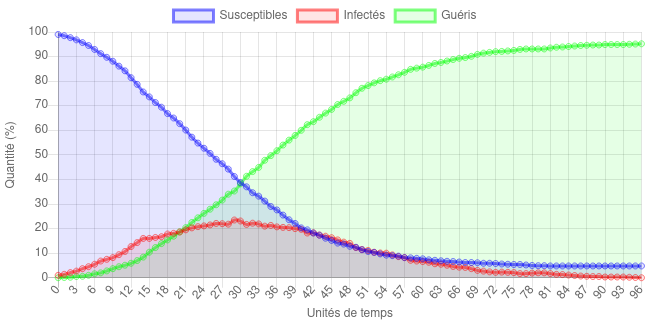
Le nombre total de personnes ayant été malades reste énorme, mais la charge pour le système de santé est plus supportable (environ 20% de personnes infectées), bien que le nombre de personnes infectées par unité de temps reste élevé très longtemps : on reste au-dessus de 10% de personnes infectées durant environ 50 unités de temps (contre environ 30 ci-dessus). À l’inverse, augmenter le rayon de rencontre a des conséquences catastrophiques : quand on prend un rayon énorme ( = 50), on monte très vite (10 unités de temps !) à 60% de personnes infectées.
En fait, en modifiant ce paramètre, on permet de simuler deux situations extrêmes :
-
En prenant = 1, on simule une transmission de proche en proche, où la maladie progresse très lentement. En fait, il faut se rendre compte que durant la simulation, on voit régulièrement apparaître des situations où une personne infectée ne peut plus infecter d’autres voisins, car ceux-ci sont déjà guéris ou en passe de l’être :
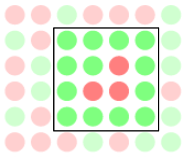
Quoi qu’il arrive, vu que =1, les trois personnes infectées à l’intérieur du carré ne peuvent infecter personne. Ces voisins agissent donc comme une barrière contre la transmission de la maladie. D’ailleurs, c’est le même effet qui explique le succès de la vaccination : si toutes les personnes que vous pouvez potentiellement infecter sont déjà immunisées, vous ne pourrez pas transmettre la maladie.
-
En prenant très grand, on simule un brassage permanent de la population, où tout le monde peut potentiellement avoir un contact avec tout le monde, ce qui rend très vite la situation ingérable : l’effet de barrière n’existe plus, puisque n’importe quelle personne susceptible peut se retrouver en contact avec une personne infectée !
Finalement, jouer sur le nombre de rencontres et sur le taux d’infection a donc des effets bénéfiques sur le contrôle de l’épidémie, même si ces effets ne sont pas tout à fait équivalents. Par exemple, voici une simulation dans laquelle le nombre de rencontre a été réduit à 1 :
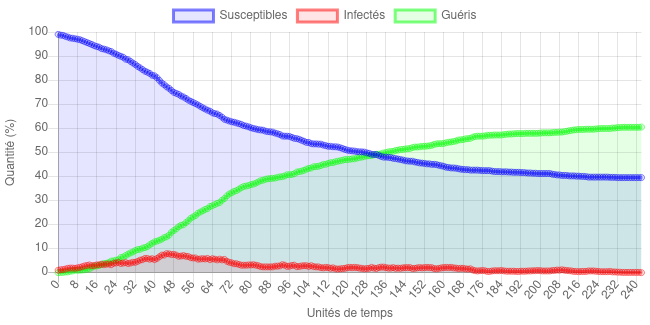
Cette fois, malgré une épidémie très longue (deux fois plus que les exemples précédents), le nombre de personnes ayant été malade n’est plus que de 60% et le nombre de personnes infectées ne dépasse jamais les 10%. Et si, cette fois, on diminue tout en gardant le nombre de rencontres à 4 :
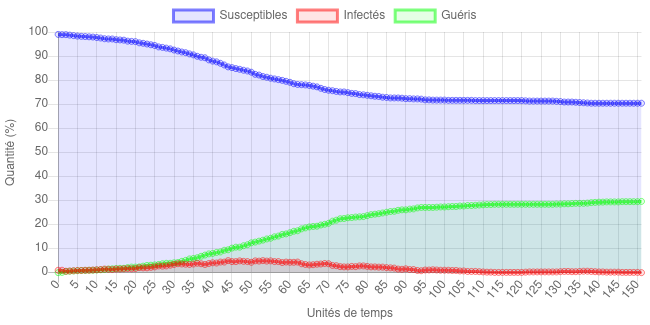
Avec ce choix de paramètres, on a carrément inversé la tendance, puisque la maladie n’a touché qu’à peu près 30% de la population.
Notez qu’on peut même arriver à une situation où la maladie ne se propage pas énormément. En gardant = 1, cela arrive dès que . Par exemple,
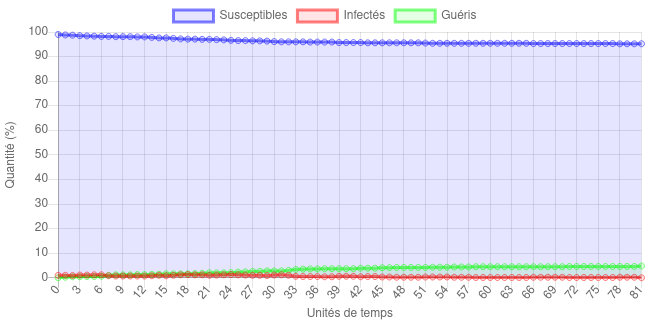
C’est évidemment une situation idéale ! On expliquera plus loin pourquoi c’est le cas.
Conclusion
Le résultat est sans appel : pour lutter contre l’épidémie, il est nécessaire d’éviter au maximum que la maladie se propage. André sait que ces mesures ne le rendront pas populaire, mais il est prêt : si jamais la maladie devait se déclarer sur l’île, ce sera confinement pour tout le monde !
Vous me voyez venir, ce genre de modèle invite très clairement à prendre des mesures drastiques. Ainsi,
-
Pour réduire , il s’agit de favoriser toute forme de prophylaxie (tout processus évitant l’apparition ou la propagation d’une maladie). Par exemple : port du préservatif pour une MST, port du masque pour une infection respiratoire, désinfection systématique de certains objets, lavage des mains et hygiène corporelle, etc.
-
Pour réduire et , on va augmenter la distance sociale, en évitant les lieux de rencontre, voir en confinant carrément la population le cas échéant. Par exemple, voici ce qui se passe si, après 10 étapes de simulation, on change brusquement et :
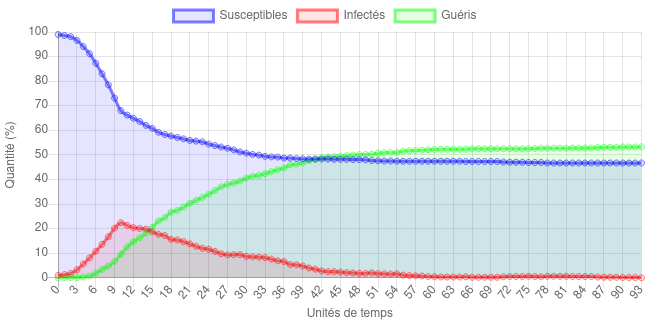
Exemple de simulation où on passe de à (avec = 1%, = 20%, = 10%) pour simuler l’effet d’une mesure de distanciation sociale. C’est, sur le papier, relativement efficace si tout le monde joue le jeu.
-
Pour augmenter (donc réduire ), il faut essayer de trouver des traitements efficaces. C’est clairement la partie la plus complexe, puisque la recherche d’un traitement prend énormément de temps. C’est aussi la raison pour laquelle on se rabat souvent sur les deux autres types de mesures, par manque de traitement efficace.
- Ou, de manière complémentaire mais pas tout à fait équivalente, que les contacts se font sur le début de la période de contagion, lorsque les symptômes ne sont pas encore apparus.↩
- C’est l’espérance mathématique.↩
- Ces paramètres varient énormément en fonction de la maladie qui est traitée.↩
- Calculé avec https://vrcacademy.com/calculator/negative-binomial-distribution-calculator/.↩
- Nombre basé sur la densité de médecins en France (source)↩
- Principalement parce que les effets de bord sont plus marqués.↩
Approche déterministe : modéliser et comprendre
Guy et André sont assez contents de la simulation, car elle permet de voir l’effet des différents paramètres d’une pression de bouton. Néanmoins, le caractère aléatoire rend difficile l’interprétation des résultats de manière précise. Heureusement, Louise a maintenant eu le temps de ressortir son syllabus1 d’analyse. Et elle a des choses à leur montrer et à leur apprendre !
Le modèle SIR revisité
Reprenons : on a donc 3 compartiments, une probabilité de passer du premier au second et une probabilité de passer du second au troisième.

Des équations différentielles ?
Une autre approche du modèle SIR consiste à s’intéresser à l’évolution macroscopique des différentes populations, sans regarder à l’échelle de l’individu. Par exemple, prenons le nombre de personnes qui guérissent à un point donné de la simulation : on peut connaître ce nombre en calculant
avec plus ou moins petit. Il semble assez logique que soit proportionnel à : si on attend longtemps entre deux étapes, le nombre de personnes guéries dans l’entre deux sera plus grand que si on regarde fréquemment. De même, on sait que cette grandeur est proportionnelle à , puisque plus est grand, plus les personnes guérissent vite. Finalement, on peut imaginer que ce nombre est proportionnel au nombre de personnes infectées : si personne n’est infecté, personne ne guérit. Dès lors, on a
Si on divise tous les membres de l’égalité par , afin d’obtenir la variation de au cours du temps, on a
ce qui, si on considère un très petit, revient à la définition d’une dérivée, notée ou encore . Puisqu’il s’agit de la variation de au cours du temps, une autre manière de voir cette quantité est de le définir comme la vitesse à laquelle les personnes guérissent. Pour ceux dont les cours de maths seraient loin, petit rappel : la dérivée d’une fonction en un point décrit en fait la pente de la fonction en ce point, autrement dit son évolution, ici dans le temps. Par exemple, regardons l’évolution de la courbe des personnes guéries dans la simulation ci-dessous :
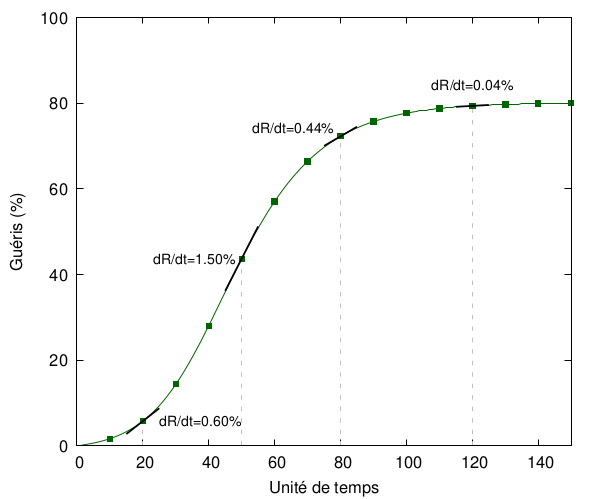
La dérivée représente ici le taux de guérison par unité de temps : plus cette dérivée est importante, plus le nombre de personnes guéries augmentera vite. On voit que celle-ci est faible au début, augmente ensuite (+1,5% de personnes guéries par unité de temps à = 50), puis diminue et tend en fait vers (avec ). Les zones où la dérivée est faible correspondent donc à des plateaux, ceux où la dérivée est importante à des modifications importantes.
En sachant que les deux autres populations (susceptible et infectée) dépendent aussi du nombre de personnes susceptibles, vu que s’il n’y en a plus alors il n’y a pas de nouvelles infections, mais aussi du nombre de personnes infectées, puisque s’il n’y en a plus alors il ne peut plus y avoir d’infection, le même raisonnement conduit à la définition suivante pour le modèle SIR :
C’est ce qu’on appelle un système d’équations différentielles.
Notez que par rapport à ce qu’on a fait précédemment, on ne considère donc non plus les individus séparément mais la population dans son ensemble. Les paramètres et ne peuvent plus être intégré de manière simple dans ce modèle (on part du principe que et ). Dès lors, l’effet éventuel des différentes mesures sera modélisé par la modification de et !
Une simulation, encore une !
Pour connaître la population dans un compartiment donné à un moment donné, il faut résoudre le système ci-dessus, en faisant le procédé inverse de la dérivée, l’intégration. Malheureusement, on n’a pas de solution analytique (simple) au problème ci-dessus, il faut donc se résoudre à l’intégrer de manière numérique. L’idée est assez simple : si on a, pour toute fonction dépendante du temps ,
avec une constante quelconque, alors
On peut donc s’amuser à calculer à partir de (avec ) en approchant de par petits pas (avec un pas trop grand). C’est le principe de la méthode d’Euler, qui a déjà été abordée par @Aabu dans son tutoriel. Ceci dit, pour des questions de stabilité, j’ai utilisé une des méthodes de Runge-Kutta (la plus connue, rk4), basée sur le même principe.
Vous pouvez retrouver la simulation ici:
Un nouveau type de graphe fait donc son apparition : le graphe susceptibles-infectés, présentant la trajectoire de l’épidémie c’est-à-dire le nombre de personnes infectées en fonction du nombre de personnes susceptibles. Ce dernier graphe permet dès lors de visualiser plus facilement l’évolution de l’épidémie. Par exemple,
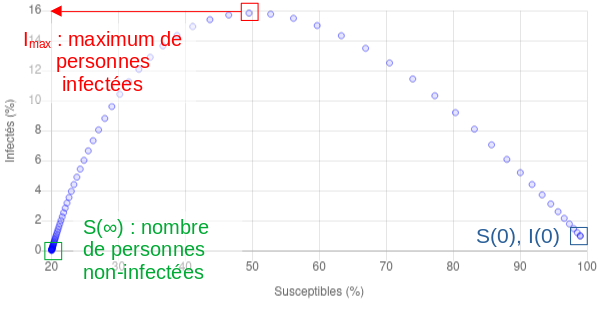
On peut dès lors facilement voir l’effet du paramètre sur l’évolution de l’épidémie :
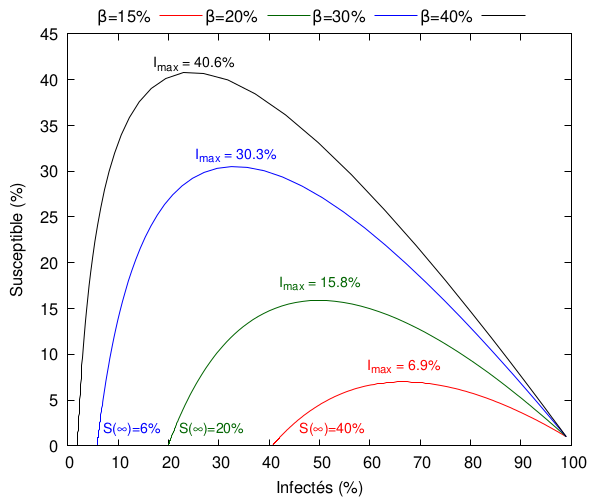
De manière peu surprenante, l’augmentation de est corrélée avec une augmentation du pic épidémique, ainsi que la réduction du nombre de personnes non-infectées.
Le nombre de reproduction
Reprenons nos équations :
Comme on l’a vu ci-dessus, puisque , la population de personnes susceptibles ne peut que baisser au cours du temps, tandis que celle de personnes guéries ne peut qu’augmenter au cours du temps, vu que . Par ailleurs,
ce qui signifie que la population, elle, reste constante dans l’absolu: aucune personne ne disparaît ou n’apparaît, il y a seulement des mouvements d’un compartiment à l’autre.
Le signe de est beaucoup plus intéressant : en effet, comme on vient de le voir, la maladie ne se propage que lorsque cette fonction est positive, puisque dans le cas contraire, le nombre de personnes infectées diminue inexorablement. Regardons donc plus en détail le graphe correspondant :
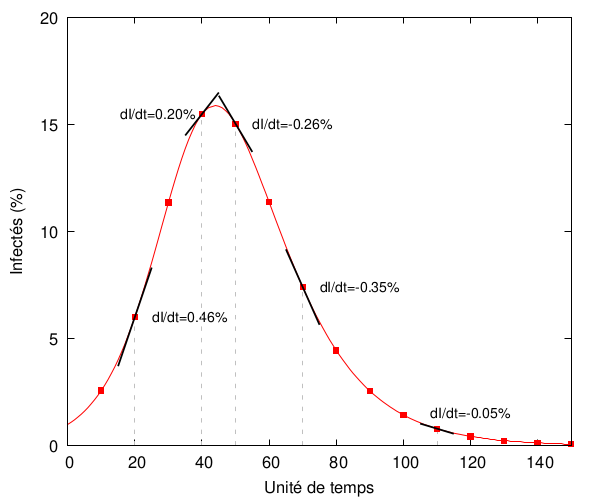
On voit que dans cet exemple, au-delà de , la dérivée devient négative : le nombre de personnes infectées diminue. Cette diminution est de plus en plus importante (valeur fortement négative, forte diminution) et puis diminue (avec, bien entendu, ).
Définition de
On a donc augmentation de la population de personnes malades si
avec est appelé le nombre de remplacement :
Il s’agit du nombre de personnes infectées par un individu contagieux, au temps . Notez que ne fait que baisser au cours de la simulation, vu que ne fait que diminuer. Au début de la simulation, vu qu’on a , on peut alors définir le nombre de reproduction de base, le fameux , comme étant
qui est le nombre moyen de personnes qu’infecte une personne malade tant qu’elle est contagieuse : si , un malade infectera moins d’une personne et la maladie disparaîtra d’elle même. À l’inverse, la maladie se propage si .
En effet, si on considère petit, on a et donc . En intégrant, on obtient
Dès lors, si , alors décroît et inversement.
Par exemple, pour = 20% et = 10%, on trouve que , donc l’épidémie se propagera. Notez également que . Il y a ceci dit un intérêt à suivre au cours du temps pour voir comment la situation épidémique évolue. Si ça vous intéresse, avec un petit bagage de statistique, c’est par là.
Études de solutions partielles
Malheureusement, on ne peut pas, à partir du système d’équation ci-dessus, obtenir de solution analytique à notre système. Autrement dit, il n’est pas possible d’obtenir, par exemple pour , une expression qui ne fasse intervenir que et . On peut ceci dit étudier des solutions partielles en considérant des cas ou une quantité est fonction d’une autre, qui sont facile à obtenir.
Ainsi, on peut étudier l’évolution de en fonction de , afin de comprendre l’évolution du graphe susceptible-infecté donné plus haut.
En effet,
qui a le bon goût d’être une équation différentielle séparable, possédant dès lors une solution, à savoir
avec une constante. En , et (, personne n’est immunisé !), on a
et donc,
Ainsi,
-
Nombre maximal de personnes infectées : il s’agit de rechercher le maximum de , qu’on obtient comme on l’a vu plus haut lorsque … Autrement dit lorsque , c’est-à-dire . Si on substitue cette seconde option dans l’équation de , on trouve
Grâce à cette équation, on peut donc estimer le nombre maximum de personnes malades au même moment. Par exemple, pour et = 99%, on trouve = 15,8%.
-
Immunité de groupe : "l’immunité de groupe" (ou, plutôt, le seuil d’immunité de groupe) est définie comme le moment où le pic d’infection est maximal, ce qu’on vient de calculer au point précédent. Il s’agit donc du point où , c’est-à-dire où
Pour un de 2, il s’agit donc du point où 50% de la population est infectée ou l’a été. Notez bien que cela ne signifie pas que l’épidémie est terminée (loin de là !), juste que le nombre d’infection ne fera que de diminuer.
-
Nombre de personnes non-infectées en fin d’épidémie : compte tenu que , on trouve que
Malgré son apparente simplicité, cette équation ne possède pas de solutions analytiques simples. Néanmoins, on peut en estimer numériquement la solution (il y en a 2, mais évidemment, seule celle qui donne est intéréssante). Par exemple, pour = 2 et = 99%, on trouve 20%. En comparaison avec le seuil d’immunité de groupe pour le même , on voit qu’il aura encore fallu 30% de malade pour achever l’épidémie.
L’évolution de ces quantités, ainsi que quelques autres, avec est tracée ci-dessous :
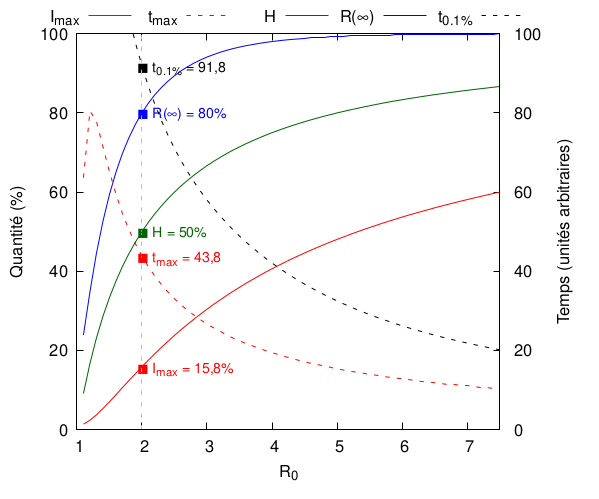
On voit très clairement que plus augmente, plus la situation est catastrophique : le pic épidémique survient de plus en plus tôt et est de plus en plus grave. Le seuil d’immunité de groupe augmente lui aussi avec : il est déjà de 50% pour = 2. Par ailleurs, le nombre de personnes ayant contracté la maladie à la fin de l’épidémie monte très vite à (quasiment, vu qu’il ne peut l’atteindre) 100%. Enfin, le retour à la normale est d’autant plus brutal, puisque le temps qu’il faut pour repasser sous la barre de 0,1% de personne nouvellement infectées diminue avec et donc plus est faible plus l’épidémie est longue.
Notez finalement la différence entre la courbe verte (immunité de groupe) et la courbe bleue (personnes guéries) : le seuil d’immunité de groupe ne signifie absolument pas la fin des ennuis !
Un résultat surprenant intervient lorsque qu’on étudie en fonction de :
qui est également séparable et donc intégrable:
avec une constante. Vu qu’en , on a , on obtient
vu que si on prend le cas , on peut écrire que . Dès lors, même si , , ce qui donne une borne inférieure à : certaines personnes ne seront jamais infectées quoi qu’il arrive. Pour et = 99%, on trouve 13,3%.
Évidemment, tenter l’immunité de groupe, c’est facile : on laisse faire les choses et la maladie s’éteindra d’elle-même. C’est même totalement une stratégie acceptable pour le rhume. Oui, mais tout dépend des effets de la maladie : on survit assez bien à un rhume et ça n’empêche même pas spécialement les gens de vivre, au pire ils sont plus fatigués, au pire du pire ça finit en état grippal. Le danger, et on ne le dira jamais assez, c’est d’en arriver à un point où le système de santé ne peut plus traiter les malades et est obligé de faire des choix : quand on est dans la force de l’âge en pleine santé, il est facile que dire que seuls les patients les plus faibles mourront… Jusqu’à ce que ça tombe sur un de vos proches.
Oui, mais si on… Meure ?
André fait tout de même remarquer à son frère et sa fille que malheureusement, la vie ne s’arrête pas pendant une épidémie. On peut empêcher que les gens se rencontrent, on ne peut évidemment pas empêcher qu’ils naissent et encore moins qu’ils meurent (de tout autre chose). Pas de problème, Louise est sur le coup.
Tentons d’améliorer le modèle sans changer le nombre de compartiments et introduisons une nouvelle probabilité : , modélisant le taux de mortalité (non dû à la maladie)… Et de naissances. En effet, on est obligés de partir du principe que le taux de mortalité et de naissance est le même pour conserver une population constante : ce n’est par exemple pas le cas en France, où on a un taux de mortalité de moins de 1% par an,2 contre un taux de natalité d’un peu plus de 1% par an, donc une légère croissance.3
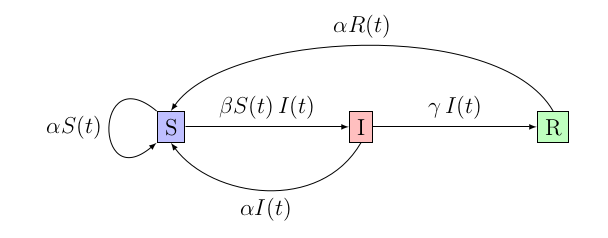
On en arrive au système suivant :
De la même manière que pour le système SIR simple, on peut facilement définir un nombre de reproduction comme étant
qu’on va ici nommer taux effectif de reproduction. En effet, ce système, avec lequel vous pouvez également jouer sur la simulation ci-dessus (il y a un curseur pour le taux de mortalité), a une propriété intéressante : il possède une solution d’équilibre endémique.
Une situation d’équilibre correspond au cas où les populations ne bougent plus en apparence :
ce qui ne signifie pas forcément que plus rien ne se passe : juste que le nombre de personne dans chaque compartiment reste constant passé un certain temps. Posons qu’à cette situation d’équilibre correspond le nombre de personnes susceptibles et le nombre d’infectés . Une situation d’équilibre endémique correspond au cas où . Ceci dit, puisque , alors
et donc soit = 0%, ce qui était déjà le cas avec le modèle SIR, soit
ce qui, rappelez-vous, correspond à la situation de maximum épidémique pour le modèle SIR où = 0%. De même, vu que ,
Et, dès lors,
Cette dernière relation montre bien qu’un équilibre endémique n’est pas possible si (vu que cela résulterait en , ce qui n’a pas de sens épidémiologiquement parlant). Par contre, il est possible dès que et on peut même prouver que cet équilibre est stable, c’est-à-dire que si rien n’est fait, la maladie reste en permanence dans la population, infectant au fur et à mesure les nouveau-nés.
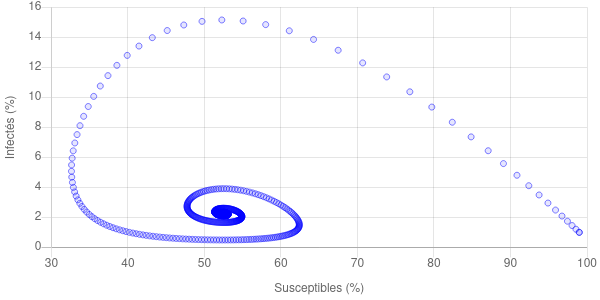
L’équilibre endémique se voit très bien sur la trajectoire de l’épidémie. Par exemple,
L’évolution de et en fonction de est détaillée ci-dessous :
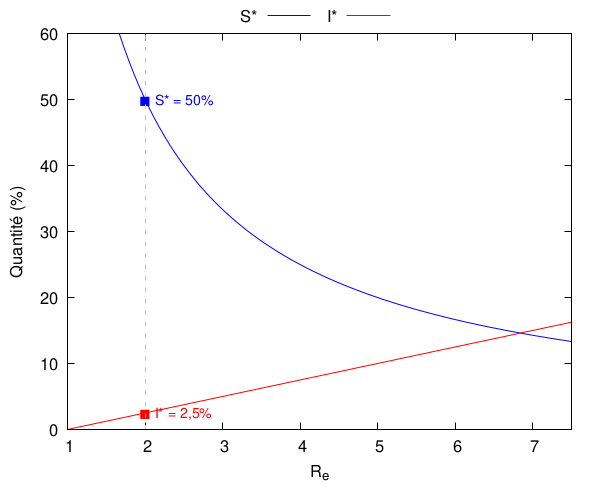
Vu l’expression, on voit très bien que est directement proportionnel à . Heureusement, en pratique, cette constante est minuscule, puisqu’on a parlé plus haut d’un taux d’à peu près 1% de naissances par an : ramené sur un jour, ça fait à peine = 0,0027%… Soit = 0,013% pour = 20% et = 2 : c’est négligeable sur de petites populations, moins à l’échelle d’une grande ville ou d’un pays.
Conclusion
Dans cette seconde partie, on a pu voir que l’analyse mathématique du modèle SIR (dans l’hypothèse d’un brassage total de la population) permettait de mettre en évidence le nombre de reproduction, et son importance pour la détermination de plein de points clés de l’épidémie. On a aussi vu que si on tenait compte du taux de mortalité, on finissait avec une solution endémique… Même si ce n’est pas trop grave au vu du très faible impact en pratique.
Bien entendu, ces prédictions doivent en pratique s’accompagner d’interprétations : gérer, par exemple, 2% de nouvelles infections par jour, c’est différent s’il s’agit d’un rhume, de la grippe ou de la malaria !
Au delà du modèle SIR
- Donc, si je comprends bien, le taux de mortalité, ce n’est pas très important ?
- Non, ça devrait aller, papa.
- Mais ces situations endémiques, là, ça peut arriver quand même ?
- Ça peut…
- Ah ! Et t’aurais quelque chose pour les gens qui se mettent en quarantaine ?
- Ça doit pouvoir se faire…
Une fois qu’on a compris le principe, on peut évidemment multiplier le nombre de compartiments et de transitions entre ceux-ci : tant qu’on arrive ensuite à raccrocher le modèle à une réalité, ça reste prédictif. Ici, on va plus particulièrement s’intéresser à l’influence de l’immunité et à celle de la détection des malades.
Immunité limitée : encore un peu de situations endémiques ?
En fait, on obtient systématiquement des situations endémiques lorsqu’on a une boucle. Une première possibilité est le modèle le plus simple, le modèle SIS :
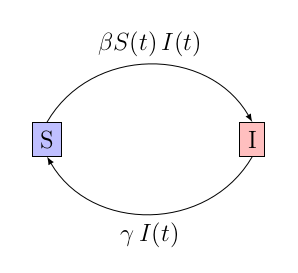
Probablement l’un des seuls modèles pour lequel on ait une solution, celui-ci modélise le cas où il n’y a pas d’immunité après la période d’infection, ce qui est le cas par exemple pour la grippe ou le rhume.1
À partir du schéma, on trouve facilement que le système est spécifié par
Notons d’ores et déjà qu’on peut définir un nombre de reproduction :
qui conduit en fait à une situation endémique si . Dès lors, si on cherche les solutions pour et vu que ,
De manière plus générale, on peut partir de pour déterminer une solution à ce problème :
où on a posé . On obtient
vu qu’on a quelque chose qui ressemble à une fonction logistique, on commence par faire un changement de variable : , donc ,
où . Autrement dit,
Si on introduit le fait que en , on a , on obtient
Et donc,
ou, plus simplement,
grâce à la définition de donnée plus haut. On voit assez vite que, si ,
- en on obtient bien et
- , vu que .
On a donc une situation épidémique qui évolue de à et qui n’en bouge plus. Par exemple,
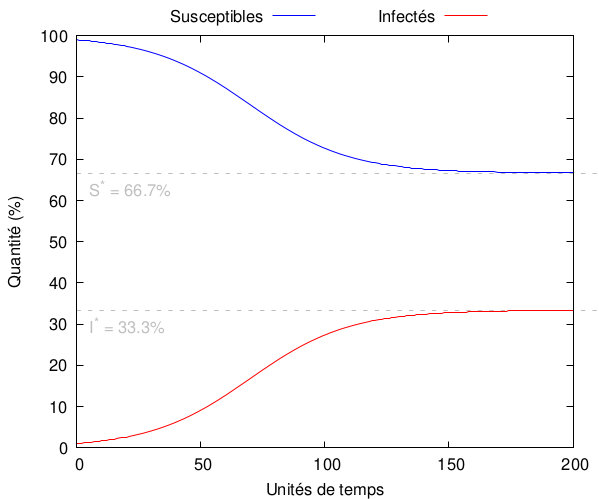
In fine, ça signifie que dans l’absolu tout le monde y passe et qu’il est évidemment possible d’y passer plusieurs fois.
Un autre cas de variations cyclique provient du cas où l’immunité existe, mais n’est que temporaire : c’est le modèle SIRS.
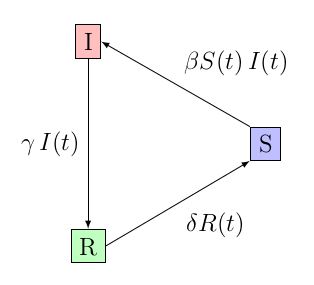
Dans ce cas, le nombre de reproduction est également
qui, quand conduit à une situation endémique cette fois caractérisée par
ce qui revient bien au modèle SIR d’origine pour = 0. Et en pratique, ça donne par exemple ceci :
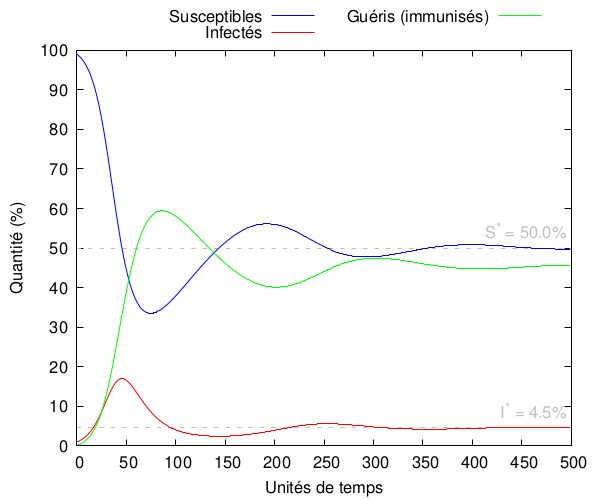
On voit qu’on retrouve dans ce cas un comportement ondulatoire (avec plusieurs pics épidémiques de moindres amplitudes) similaire à l’inclusion du taux de mortalité. Ceci dit, notez bien que le nombre d’infection finit malgré tout par se stabiliser autour de : on a dans ce cas des oscillations amorties. Une fois encore, les périodes d’immunité sont généralement très longues ( très petit), donc le modèle SIR suffit.
Pour avoir des épidémies régulières, ce qui arrive par exemple dans le cas de la grippe (une épidémie par an en hiver), on peut repartir du modèle SIS et introduire un taux d’infection variable , modélisant le fait que les défenses immunitaires sont moins efficaces à certaines périodes de l’année. Par exemple,
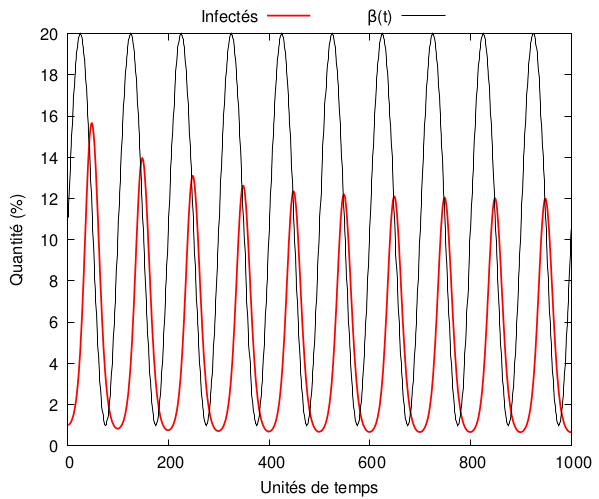
Incubation et quarantaine
Sur le modèle SIR de base, on peut également rajouter une période d’incubation, durant laquelle la personne infectée n’est pas encore contagieuse. C’est d’ailleurs le cas pour bien assez de maladies, où la contagiosité ne se développe qu’après quelques jours.
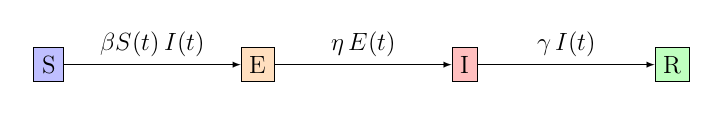
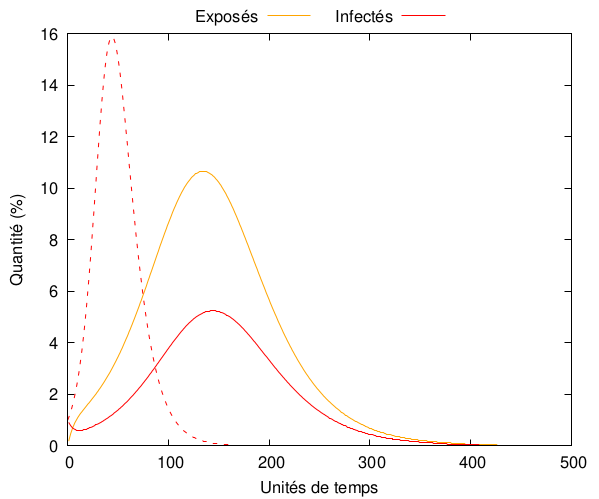
Le nombre de reproduction reste le même et le système ne présente pas de situation endémique. Par contre, par rapport au modèle SIR avec les mêmes paramètres, on voit un délai apparaître, ainsi qu’un élargissement de la courbe :
Néanmoins, on peut profiter de cette période d’incubation pour tenter de détecter les (futures) personnes infectieuses et tenter de les mettre en quarantaine pour éviter qu’elles en infectent d’autre. On peut alors imaginer le circuit suivant.
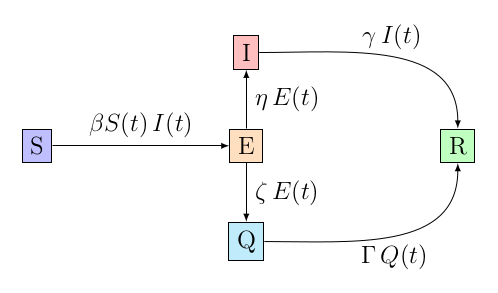
Dans ce cas, détermine le nombre de jours moyen que restera une personne exposée avant d’être mis en quarantaine. Évidemment, plus est grand, plus la détection et la mise en quarantaine sera efficace. Par la suite, on a généralement , puisque la période d’infectiosité ne change normalement pas avec la mise en quarantaine et que si la personne est mise plus tôt que le moment où elle est infectieuse, elle devra rester plus longtemps en quarantaine. Dans l’absolu, on a donc , afin que la probabilité de chaque branche soit équivalente, mais on pourrait très bien imaginer guérir plus vite si la maladie est détectée plus tôt.
Par exemple,
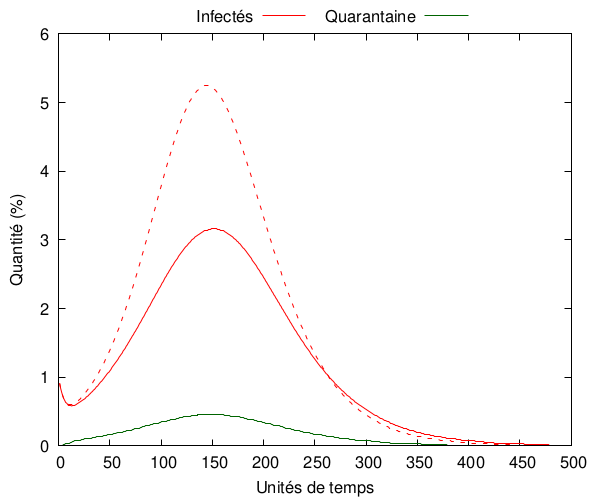
On voit bien que toute mise en quarantaine, même faible, est une amélioration
Conclusion
… Et ainsi de suite. Le tout est de bien étudier les différents mécanismes de la maladie afin de déterminer des catégories adéquates. Par exemple, dans le cas du SIDA, on n’a pas d’immunité, mais plusieurs stades d’infectiosité avec des taux différents. Dans le cas de la malaria, on inclut également la population de moustiques, vecteurs de la maladie, etc. C’est un sujet de recherche très vaste !
Bref, toute info supplémentaire sur la maladie est la bienvenue : le modèle SIR considère une immunité ad vitam æternam, et pas d’incubation. Le problème, c’est que dans le cas d’une nouvelle maladie, les infos mettent du temps à arriver, ce qui pousse de manière assez logique à privilégier un confinement généralisé ( et peuvent être déterminés assez vite) jusqu’à avoir plus d’infos.
- Plutôt parce que l’immunité ne fonctionne pas vu que les souches ont une forte variabilité, mais l’effet est le même.↩
Au final, l’île s’en est bien sortie : plus tard, les journaux titreront "gestion exceptionnelle de la violite à Zeest". André, modeste, remerciera ses collaborateurs et la chance qu’il a eu de voir l’épidémie arriver de loin. Tout est bien qui finit bien… Jusqu’à la prochaine fois. Et justement, une petite maladie sans prétention commence à faire des dégâts dans la province de Wuhan en Chine. COVID-19 ? Ma foi nous verrons…
Si vous deviez retenir une chose de tout ça, c’est que "tous les modèles sont faux… mais certains sont utiles". En effet, la réalité est toujours plus complexe que n’importe lequel des modèles qu’on pourrait imaginer : c’est pour ça qu’on les appelle des "modèles", d’ailleurs.
Dans le cas qui nous occupe, on retiendra que dans le cas déterministe (seconde et troisième partie), on part du principe que la population est brassée en permanence (tout le monde croise tout le monde) ce qui en termes de maladie représente… Le pire des cas, même si en essayant de reproduire des données réelles d’épidémies passées ou présentes, on absorbe ces effets dans les paramètres. On a vu que pour résorber ces effets, il fallait partir sur des simulations stochastiques sur base de réseaux : ce qu’on gagne en précision, on le perd alors en complexité (mais c’est parfois nécessaire).
Une autre source d’approximation provient du fait que les modèles présentés partent généralement du principe qu’une fois la direction décidée (les paramètres fixés), plus rien ne change. Bien entendu, les décisions prises au cours de l’épidémie changent parfois radicalement les paramètres et donc l’évolution des prédictions. Les simulations doivent donc être réévaluées en permanence.
Merci à @Holosmos et @Ekron pour la validation, à @Amaury et @STalone pour JSFiddle et @QuentinC pour les commentaires.
Tous les scripts et schémas utilisés dans ce tutoriel sont disponibles sur Github sous licence CC-BY.
Sources utilisées : outre Wikipédia,
- Y. Okabe et A. Shudo Mathematics 8, 1174 (2020), 10.3390/math8071174.
- C. M. Simon PeerJ Physical Chemistry 2, e14 (2020), 10.7717/peerj-pchem.14
- S. Ansumali et al. Annual Review in Control 50, 432 (2020), 10.1016/j.arcontrol.2020.10.003.
- La série d’articles Epidemic Modeling sur la modélisation du COVID-19, de B. Gonçalves sur Médium : partie 1, 2, 3 et 4.
- G. Bastin, Lectures on Mathematical Modelling of Biological Systems, https://perso.uclouvain.be/georges.bastin/lectures-bio.pdf (dernière consultation le 9 février 2021).




