Piles et files

• Quelques autres structures de données courantes
• Sommaire
• Arbres

On a vu que les listes représentaient des suites d'éléments que l'on pouvait facilement agrandir ou rétrécir selon ses besoins. Il se trouve qu'en pratique, certaines manières d'ajouter ou d'enlever des éléments reviennent très souvents, et on leur a donc donné un nom pour les repérer plus facilement : les piles et les files.

• Concept
• Mise en pratique

Concept

Imaginez que l'on manipule une liste d'éléments qui évolue au cours du temps : on peut en ajouter et en retirer. Supposons que l'on ajoute toujours les éléments au début de la liste. Pour retirer les éléments, il y a deux possibilités simples qu'il est intéressant d'étudier :

• le cas où on retire toujours les éléments au début de la liste
• le cas où on retire toujours les éléments à la fin de la liste

Ces deux cas de figures se retrouvent très souvent dans la vie de tous les jours. Dans le premier cas, on dit qu'on utilise une structure de pile, dans le deuxième cas une structure de file.

Par exemple, imaginez qu'un professeur a donné un devoir à ses élèves, à faire en temps limité. Un peu avant la fin, certains élèves commencent à rendre leur copie en avance. Le professeur décide de commencer à corriger les copies qu'il reçoit, pour gagner du temps. Il y a une pile de copies sur son bureau, et :

• quand un élève a terminé, il rend sa copie au professeur qui la pose sur la pile de copie
• quand il a terminé de corriger une copie, il prend la première copie sur la pile pour la corriger

Cela correspond bien à ce que j'ai appelé une pile. On décrit souvent ce comportement par l'expression dernier entré, premier sorti (ou LIFO, de l'anglais Last In, First Out) : la dernière copie rendue est la première à être corrigée.

Au contraire, quand vous faites la queue devant la caisse d'un supermarché, cela correspond bien à une file d'attente : les clients arrivent d'un côté de la queue (au "début de la queue"), et la caissière est à l'autre bout (à la "fin de la queue"). Quand elle a terminé de compter les achats d'un client, elle fait passer le client qui est à la fin de la queue. C'est le comportement premier entré, premier sorti (ou FIFO, First In, First Out).

Question : Imaginez un boulanger qui fait cuire du pain, le stocke puis le vend à ses clients. Les clients aiment bien avoir du pain le plus frais possible (qui sort tout juste du four), et le boulanger ne peut pas leur vendre de pain trop sec (qui est sorti du four depuis trop longtemps). Quels sont les avantages d'une pile ou d'une file dans ce cas ? Quelle structure choisiriez-vous ?

Mise en pratique

Piles

Les piles sont très simples, parce que ce sont essentiellement des listes. On a vu qu'avec une liste, il était facile d'ajouter et de retirer des éléments en tête de liste. Cela fait exactement une pile.

Voici un exemple de code C pour gérer les piles, qui réutilise le type List définit pour les listes. Pour ajouter un élément on utilise push, et pop pour enlever un élément et récupérer sa valeur.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

typedef List *Stack;

Stack *new_stack(void)
{
    Stack *stack;
    if ((stack = malloc(sizeof *stack)) == NULL)
        return NULL;
    *stack = NULL;
    return stack;
}

void free_stack(Stack *stack)
{
    free_list(*stack);
    free(stack);
}

int stack_is_empty(Stack *stack)
{
    return *stack == NULL;
}

int stack_push(Stack *stack, int elem)
{
    List *pushed;
    if ((pushed = cons(elem, *stack)) == NULL)
        return -1;
    *stack = pushed;
    return 0;
}

int stack_pop(Stack *stack, int *elem)
{
    List *tail;
    if (*stack == NULL)
        return -1;
    tail = (*stack)->next;
    *elem = (*stack)->val;
    free(*stack);
    *stack = tail;
    return 0;
}

La même chose en Caml :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

let new_stack () = ref []

let stack_is_empty stack = 
  !stack = []

let stack_push stack elem =
  stack := elem :: !stack

let stack_pop stack =
  let old = !stack in
  stack := List.tl old;
  List.hd old

N'hésitez pas à le recoder dans votre langage préféré. Même si ça existe déjà dans la bibliothèque standard, ça fait toujours un peu d'entraînement.

Files

Les files sont un peu plus délicates : si on retire les éléments en tête de liste (au début de la liste), il faut ajouter les éléments à la fin de la liste. C'est quelque chose que l'on ne fait pas d'habitude, car ce n'est pas pratique : dans une liste, on connaît le premier élément, mais pour accéder au dernier élément il faut parcourir toute la liste jusqu'à la fin, ce qui est lent (complexité linéaire). On va donc créer une structure supplémentaire, qui contient une liste, mais qui stocke aussi la cellule correspondant à son dernier élément, pour pouvoir y accéder (et rajouter de nouveaux éléments derrière).

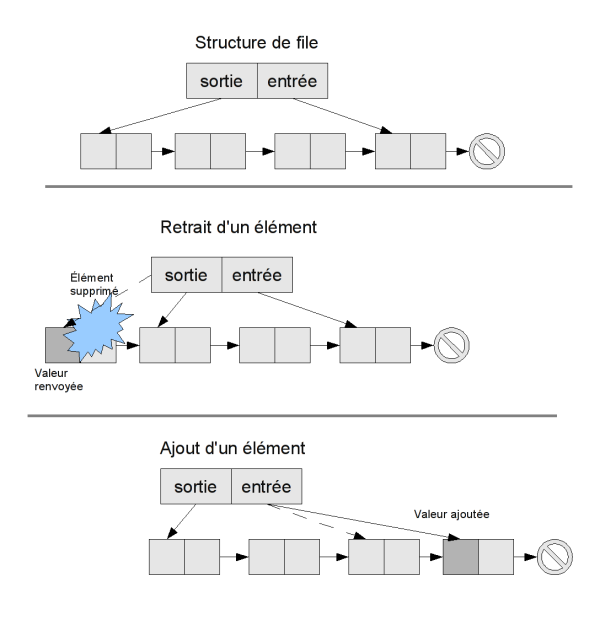
Remarque : pour définir les piles et les files, j'ai parlé d'ajouter les éléments en début de liste, et de les retirer soit au début (pour les piles) soit à la fin (pour les files). Mon implémentation concrète des files va en fait dans l'autre sens : je retire les éléments en début de liste, et je les ajoute à la fin. Bien sûr, ça ne change rien au comportement de la file.

Exercice : Codez les opérations push et pop pour une file (ou queue, terme utilisé en anglais) dans votre langage préféré.

Correction en C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

struct queue
{
    List *input;
    List *output;
};

typedef struct queue Queue;

Queue *new_queue(void)
{
    Queue *queue;
    if ((queue = malloc(sizeof *queue)) == NULL)
        return NULL;
    queue->input = NULL;
    queue->output = NULL;
    return queue;
}

void free_queue(Queue *queue)
{
    free_list(queue->output);
    free(queue);
}

int queue_is_empty(Queue *queue)
{
    return queue->input == NULL;
}

int queue_push(Queue *queue, int elem)
{
    List *cell;
    if ((cell  = cons(elem, NULL)) == NULL)
        return -1;
    if (queue_is_empty(queue))
        queue->output = cell; /* output was NULL, set it to the single cell */
    else
        queue->input->next = cell;
    queue->input = cell;
    return 0;
}

int queue_pop(Queue *queue, int *elem) {
    List *cell;
    if ((cell = queue->output) == NULL)
        return -1;
    *elem = cell->val;
    queue->output = cell->next;
    if (queue->output == NULL) /* empty queue */
        queue->input = NULL;
    free(cell);
    return 0;
}

Correction en caml :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

type 'a mutlist = { elem : 'a; mutable next : 'a mutlist option }
type 'a queue = ('a mutlist * 'a mutlist) option ref

let new_queue () = ref None

let queue_is_empty queue =
  !queue = None

let queue_push queue elem =
  let cell = { elem = elem; next = None } in
  queue := match !queue with
  | None -> Some (cell, cell)
  | Some (input, output) ->
      input.next <- Some cell;
      Some (cell, output)

let queue_pop queue = match !queue with
| None -> failwith "empty queue"
| Some (input, output) ->
    queue := (match output.next with
              | None -> None
              | Some tail -> Some (input, tail));
    output.elem

Si vous avez des difficultés à faire cet exercice, ou à adapter les solutions à votre langage préféré, n'hésitez pas à créer un topic sur dans le forum adapté à votre langage.

La plupart des langages de programmation proposent des bibliothèques qui permettent d'utiliser des piles ou des files, sans avoir à les recoder vous-même.

Ces structures apparaissent naturellement dans un certain nombre de problèmes ou de situations de tous les jours, et nous les rencontrerons à nouveau par la suite, au sein d'algorithmes plus compliqués.

• Quelques autres structures de données courantes
• Sommaire
• Arbres