Combien d'énergie peut-on extraire du vent ?

Pour calculer l’énergie extraite du vent par une éolienne, il faut déjà savoir combien d’énergie est transportée par le vent. Dans cette partie, nous allons donc calculer la puissance du vent, sans éolienne pour le freiner.

Modélisation du problème

Le vent est une masse d’air en mouvement et donc comme toute masse qui se déplace, il est doté d’une énergie cinétique, qu’on appelle dans ce cas énergie éolienne.

Dans la réalité, le vent est capricieux et présente des tourbillons, bourrasques et turbulences, mais nous ferons une hypothèse simplificatrice : il soufflera dans une seule direction, régulièrement, sans tourbillons ni turbulences, à la vitesse $v$, tel une rivière paisible. Nous considérons aussi qu’il n’y a pas de zones de haute ou de basse pression et donc la masse volumique $\rho$ du vent est constante.

Ce courant d’air sera à terme intercepté par une éolienne, qui occupera une certaine surface $S$. Le vent qui souffle ailleurs ne nous intéresse pas, donc nous ne considérons que le vent soufflant à travers cette surface. Faites cependant bien attention : il n’y a pour l’instant pas d’éolienne et la surface est libre de tout obstacle.

Pour avoir la situation la plus favorable, nous supposerons que le vent traverse la surface perpendiculairement, comme schématisé ci-dessous. En effet, si la surface était inclinée, moins d’air la traverserait, le cas extrême étant celui où la surface est parallèle au vent et l’air ne traverse pas du tout la surface.

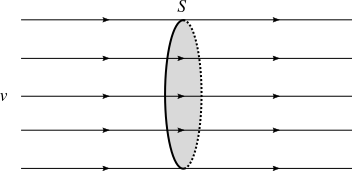
Calcul de la puissance du vent, sans éolienne pour le freiner

Pendant une certaine durée, la surface est traversée par une certaine masse d’air, dotée d’une certaine énergie cinétique. Autrement dit, la surface est traversée par une certaine quantité d’énergie par unité de temps, ce qui correspond à la puissance cinétique de l’air traversant la surface. Nous allons la calculer pour un courant d’air traversant une surface $S$ sans être freiné.

Pour rappel, une masse $m$ se déplaçant (sans rotation) à une vitesse $v$ a une énergie cinétique $E_c$ qui vaut :

$E_c = \frac{1}{2} m \, v^2.$

Nous allons appliquer cette formule à la masse d’air traversant la surface pendant une durée $\mathrm{\Delta}t$, qui aura une énergie cinétique $\mathrm{\Delta}E_c$. Le volume d’air concerné est celui « assez proche » de la surface pour la traverser pendant la durée $\mathrm{\Delta}t$, c’est-à-dire un cylindre de longueur $v\cdot\mathrm{\Delta}t$ et de section $S$.

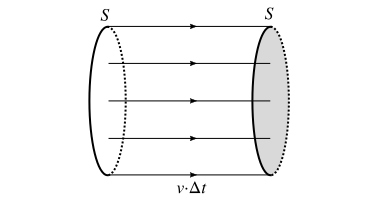
La masse de ce volume d’air est le produit de la masse volumique par le volume soit :

$m = \rho S v \mathrm{\Delta}t$

Ainsi, l’énergie cinétique de cette petite masse d’air est :

$\mathrm{\Delta}E_c = \frac{1}{2} m v^2 = \frac{1}{2} \rho S v^3 \mathrm{\Delta}t$

En divisant par $\mathrm{\Delta}t$, on obtient :

$\frac{\mathrm{\Delta}E_c}{\mathrm{\Delta}t} = \frac{1}{2} \rho S v^3$

Or, le rapport $\frac{\mathrm{\Delta}E_c}{\mathrm{\Delta}t}$ est, par définition, la puissance cinétique moyenne du flux d’air, $P_c$.

$P_c = \frac{1}{2} \rho S v^3 \quad \quad (1)$

Cette formule est importante et va nous resservir, on l’appellera maintenant « expression (1) ».

Quelques remarques sur la formule

Regardons de plus près l’expression (1) :

$P_c = \frac{1}{2} \rho S v^3$

On voit clairement qu’elle est proportionnelle :

• à la masse volumique $\rho$ de l’air ;
• à la surface $S$ ;
• au cube de la vitesse du vent $v$.

La masse volumique de l’air n’est pas le paramètre le plus déterminant, même si elle diminue avec l’augmentation de la température de l’air et de l’altitude. Elle vaut environ 1,225 kg/m³ au niveau de la mer à 15 °C, et varie usuellement 15 à 20 % en fonction du lieu d’implantation et de la saison.

Plus la surface est grande, plus on intercepte de vent, ce qui contribue au gigantisme des éoliennes actuelles, qui font jusqu’à plusieurs dizaines de mètres de diamètre ! Les éoliennes de moyenne puissance balaient une surface d’environ 6 500 m², soit approximativement la surface d’un terrain de football.

La vitesse du vent est le paramètre le plus important : elle apparaît au cube ! Elle varie grandement en fonction des lieux et peut varier entre quelques mètres par seconde et quelques dizaines de mètres par seconde. C’est pourquoi on cherche toujours à mettre les éoliennes dans les lieux les plus ventés, et avec le vent le plus régulier possible, comme en pleine mer ! Des petites différences de vitesses causent de grandes différences de puissance : un site avec un vent moyen de 10 m/s à un potentiel environ deux fois plus important qu’un site avec un vent moyen de 8 m/s.

Pour se donner une idée de l’ordre de grandeur de la puissance du vent, faisons une application numérique avec :

• $\rho$ = 1,225 kg/m³ ;
• $S$ = 6500 m² ;
• $v$ = 7 m/s, soit environ 25 km/h.

On obtient $P_c$ = 1,4 MW de puissance disponible, soit une puissance équivalente à environ 20 petites voitures.

Dans la première partie, nous avons calculé la puissance du vent à travers une surface sans qu’il soit freiné. Désormais, nous considérons que la surface $S$ contient effectivement une éolienne qui freine le vent.

Position du problème

En amont de l’éolienne, on suppose que le vent souffle à une vitesse $v_{am}$ donnée. La force avec laquelle l’éolienne freine le vent peut être contrôlée ; ainsi, la vitesse du vent en aval est un paramètre qu’on peut choisir librement entre 0 (le vent est totalement arrêté) et $v_{am}$ (le vent n’est pas du tout freiné).

Seul la masse d’air qui traverse l’éolienne va être freinée. Pour prendre en compte cette masse d’air et seulement cette masse d’air, nous allons considérer un tube de courant tel que l’air qui rentre dans ce tube est freiné par l’éolienne, et l’air qui n’y rentre pas ne sera pas affecté. Notez bien que le tube ainsi défini n’est pas un tube matérialisé physiquement, il s’agit simplement d’une frontière immatérielle séparant notre sujet d’intérêt du reste. La surface de l’entrée du tube est $S_{am}$ et la surface de sortie $S_{av}$.

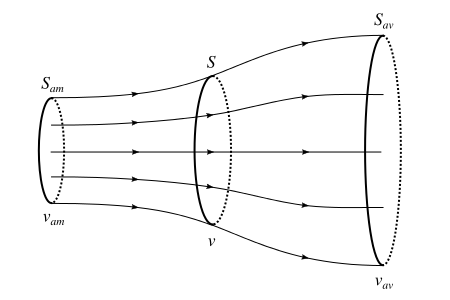
Le tube ne laisse pas l’air s’échapper, par définition, puisqu’il est défini pour englober tout l’air qui rentre jusqu’à sa sortie. Cela signifie que le débit massique est conservé : ce qui rentre dans le tube en sort également. Mathématiquement, cela se traduit par une égalité des débits massiques en entrée, au niveau de l’éolienne et en sortie.

$\rho \, S_{av} \, v_{av} = \rho \, S \, v = \rho \, S_{am} \, v_{am}$

Soit en simplifiant par $\rho$ :

$S_{av} \, v_{av} = S \, v = S_{am} \, v_{am} \quad \quad (2)$

Vous remarquerez sur le dessin que la surface de sortie est plus grande. Pourquoi ? Il faut que le débit massique se conserve, alors même que la vitesse de l’air diminue ; il y a donc deux solutions : soit l’air se comprime en augmentant sa masse volumique, soit il s’étale en occupant plus de place. Comme nous avons fait l’hypothèse que l’air était de masse volumique constante, alors l’air doit nécessairement s’étaler.

L’éolienne va freiner le vent en prélevant une partie de la puissance du flux d’air qui la traverse. Pour obtenir la puissance extraite par l’éolienne $P_t$, il faut ainsi calculer la différence entre la puissance du flux d’air en amont $P_{am}$ avec la puissance du flux d’air en aval $P_{av}$. Autrement dit :

$P_{t} = P_{am} - P_{av}$

On pourrait croire de manière naïve que pour avoir le maximum de puissance, il suffit d’avoir $P_{av} = 0$ et $P_t = P_{am}$. Mais cela ne peut pas arriver ! En effet, si l’on prélevait la quasi-totalité de la puissance du vent en amont, l’air devrait s’étaler énormément en aval de l’éolienne pour assurer la conservation du débit massique, ce qui n’est pas physiquement possible. Le vent doit ainsi avoir une vitesse non-nulle après l’éolienne et il va falloir trouver une expression de la puissance $P_t$ en fonction de $v_{am}$, $v_{av}$ et $S$, qui sont les paramètres connus ou contrôlables.

Première étape

En utilisant l’expression (1), on peut exprimer $P_t$ en fonction des surfaces et des vitesses du vent en amont et en aval.

$P_t = P_{am} - P_{av} = \frac{1}{2} \rho \, S_{am} \, v_{am}^3 - \frac{1}{2} \rho \, S_{av} \, v_{av}^3$

Soit, après factorisation :

$P_t = \frac{1}{2} \rho \left(S_{am} \, v_{am}^3 - S_{av} \, v_{av}^3 \right)$

On peut déduire de la conservation du débit massique (2) une expression de $S_{av}$ en fonction de $S_{am}$, ce qui permet d’éliminer une inconnue :

$S_{av} = S_{am} \, \frac{v_{am}}{v_{av}}$

En remplaçant cette dernière formule dans l’expression de $P_t$, on obtient :

$P_t = \frac{1}{2} \, \rho \, S_{am} \, v_{am} \left(v_{am}^2 - v_{av}^2 \right)$

Le problème maintenant est qu’on ne connaît pas $S_{am}$ ; par contre, on connaît $S$ et il est possible de trouver $v$, comme nous allons le faire dans la suite. En utilisant encore la conservation du débit massique (2), on peut avancer un petit peu, et écrire :

$P_t = \frac{1}{2} \, \rho \, S \, v \left(v_{am}^2 - v_{av}^2 \right) \quad \quad (3)$

Voilà une première expression de la puissance. On remarque qu’il y a une partie liée au débit ($\rho \, S \, v$) et une liée au ralentissement de l’air ($v_{am}^2 - v_{av}^2$). Gardez cette équation en tête, on la retrouvera un peu plus loin.

Deuxième étape

Pour continuer notre calcul, il faut se débarrasser de l’inconnue $v$. Cependant, il est impossible d’utiliser la conservation du débit massique, parce que cela réintroduirait $S_{am}$ ou $S_{av}$ dans l’expression (3). La solution vient en calculant d’une autre manière la puissance, via le travail mécanique qui est l’énergie apportée par une force lors d’un mouvement. On pourra alors résoudre une nouvelle équation pour exprimer $v$ en fonction des paramètres du problème.

En se déplaçant vers l’aval, le vent pousse la turbine, exerçant ainsi une force orientée vers l’aval. La turbine reçoit alors du travail de la part du vent. Pendant un mouvement de durée $\mathrm{\Delta}t$, l’air se déplace d’une distance $d = v\cdot \mathrm{\Delta}t$ (comme dans la première partie), tout en exerçant une force $F$. Par définition, le travail qu’il fournira à la turbine sera donc égal à :

$W_t = F d = F \, v \mathrm{\Delta}t$

En divisant par $\mathrm{\Delta}t$, on obtient la puissance mécanique cédée par l’air à la turbine en fonction de $F$ et $v$ :

$P_t = \frac{W_t}{\mathrm{\Delta}t} = F \, v \quad \quad (4)$

Pour exprimer $F$, nous allons utiliser le principe fondamental de la dynamique, qui stipule que la force est égale à la variation de la quantité de mouvement. Pour rappel, la quantité de mouvement d’une masse $m$ se déplaçant à la vitesse $v$ est $p = mv$. Si on désigne par $\mathrm{\Delta}p$ la quantité de mouvement cédée par la masse d’air traversant la turbine pendant le temps $\mathrm{\Delta}t$, on aura :

$F = \frac{\mathrm{\Delta}p}{\mathrm{\Delta}t}$

Il faut donc maintenant exprimer $\mathrm{\Delta}p$. Comme il s’agit de la quantité de mouvement cédée par la masse d’air, il s’agira de la différence entre la quantité de mouvement de cette masse d’air en amont $p_{am}$ et celle en aval $p_{av}$ :

$\mathrm{\Delta}p = p_{am} - p_{av}$

Comme on considère la masse qui traverse l’éolienne pendant le temps $\mathrm{\Delta}t$, on aura :

$p_{am} = m \, v_{am} = \rho S \, v \mathrm{\Delta}t \, v_{am}$

$p_{av} = m \, v_{av} = \rho S \, v \, \mathrm{\Delta}t \, v_{av}$

Et donc en remplaçant dans l’expression de $\mathrm{\Delta}p$ :

$\mathrm{\Delta}p = \rho S \, v \mathrm{\Delta}t (v_{am} - v_{av})$

En remplaçant dans l’expression de $F$, on obtient :

$F = \frac{\mathrm{\Delta}p}{\mathrm{\Delta}t} = \rho S \, v \, (v_{am} - v_{av})$

Finalement, en remplaçant $F$ dans l’expression (4), on obtient :

$P_t = F \, v = \rho\, S\, (v_{am} - v_{av}) v^2 \quad \quad (5)$

On peut désormais trouver $v$ ! En effet, en égalisant les deux expressions (3) et (5), on obtient l’équation suivante.

$\rho\, S\, (v_{am} - v_{av}) v^2 = \frac{1}{2} \, \rho \, S \, v \left(v_{am}^2 - v_{av}^2 \right)$

On peut en tirer facilement l’expression de $v$, en utilisant l’identité remarquable $v_{am}^2 - v_{av}^2 = (v_{am}+v_{av})(v_{am}-v_{av})$.

$v = \frac{1}{2} \left( v_{am} + v_{av} \right)$

Et maintenant, voilà l’étape finale dans le calcul de la puissance : on remplace $v$ dans l’expression de $P_t$ pour obtenir le résultat ci-dessous.

$P_t = \frac{1}{4} \rho \, S\, (v_{am} + v_{av})^2 (v_{am} - v_{av}) \quad \quad (6)$

On connaît $\rho$, $S$, ainsi que $v_{am}$. La vitesse en aval $v_{av}$ est contrôlée par l’éolienne. Il va maintenant être possible d’analyser cette formule pour voir ce qu’elle nous apprend sur le rendement des éoliennes.

Approche qualitative

La formule que l’on a déterminée dans la partie précédente est assez importante pour être écrite de nouveau :

$P_t = \frac{1}{4} \rho \, S\, (v_{am} + v_{av})^2 (v_{am} - v_{av})$

L’observation de cette formule nous indique deux choses : si le vent n’est pas freiné du tout ($v_{am} = v_{av}$), alors la puissance sera nulle. Si le vent est entièrement freiné, il en sera de même. En effet, rappelez-vous : le débit massique est conservé, et donc si $v_{av} = 0$, alors $v_{am} = 0$ également car :

$S_{av} \, v_{av} = S_{am} \, v_{am}$

Autrement dit, il y a bel et bien un optimum : si on freine trop le vent, on n’obtient pas la puissance maximale, et de même, si on ne le freine pas assez. Physiquement, il s’agit d’un compromis entre le freinage de l’air et son débit. Plus on freine l’air, plus on prend de l’énergie, mais en contrepartie, on réduit le débit, et donc on dispose de moins d’énergie.

Coefficient de puissance

On aimerait savoir quel est le maximum de puissance qu’on peut extraire du vent. Naturellement, ce maximum dépend de la puissance du vent incident $P_0$, il va donc être plus simple de calculer la proportion de puissance extractible plutôt que calculer directement la puissance extractible. Ainsi, le résultat sera indépendant de $P_0$. La proportion de puissance extraite s’appelle le coefficient de puissance et est défini comme le rapport entre la puissance de la turbine $P_t$ et celle du vent incident $P_0$.

$C_p = \frac{P_t}{P_0}$

On peut le calculer, car on connaît $P_t$ et que la première section nous a appris à calculer la puissance du vent à travers la surface de l’éolienne (expression (1)) :

$C_p = \frac{\frac{1}{4} \rho \, S\, (v_{am} + v_{av})^2 (v_{am} - v_{av})}{\frac{1}{2} \rho \, S\, v_{am}^3}$

Pour simplifier légèrement notre problème, nous allons introduire la variable $x$ définie comme le rapport des vitesses entre l’aval et l’amont.

$x = \frac{v_{av}}{v_{am}}$

Cette variable correspond à un « coefficient de freinage », qui, comme le coefficient de puissance, permet de s’abstraire de la vitesse du vent incident.

En factorisant et simplifiant comme il faut dans l’expression de $C_p$, on peut écrire la formule suivante :

$C_p(x) = \frac{1}{2} (1 + x)^2 (1-x)$

Il n’y a plus qu’une seule variable, $x$, et il va donc être très facile de calculer le maximum.

Valeur maximale du coefficient de puissance

Avant de calculer rigoureusement le maximum du coefficient de puissance, il est intéressant de voir à peu près sur un graphique comment il se présente.

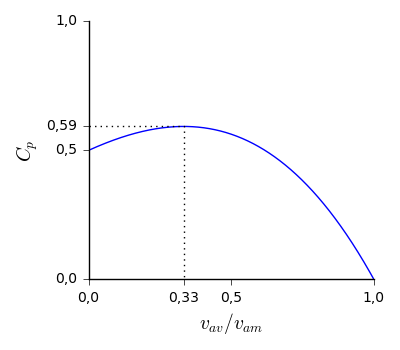
Sur ce graphique, on remarque deux choses intéressantes :

• le maximum de puissance vaut environ 0,59 et est atteint pour $x$ environ égal à 0,33 ;
• la courbe est assez plate autour du maximum, ce qui signifie qu’il est facile de rester dans une région à haut coefficient de puissance.

On peut trouver formellement le maximum du coefficient de puissance en étudiant sa dérivée par rapport à $x$, dont le calcul est laissé au lecteur à titre d’exercice. On trouve le résultat suivant :

$C_p'(x) = \frac{1}{2}(1+x)(1-3x)$

On sait que les extremums sont atteints quand la dérivée s’annule en changeant de signe. Il y a ici deux valeurs où elle s’annule : $x = -1$ et $x = 1/3$. Or, on cherche une vitesse du vent positive, donc le seul candidat valide est $x = 1/3$.

Comme $(1+x)$ est positif, et que $(1-3x)$ est positif avant $x = 1/3$ puis négatif après, on a bien un changement de signe et donc un extremum. Comme le changement s’effectue de positif vers négatif, il s’agit d’un maximum qui vaut :

$C_{p, max} = \frac{1}{2} (1 + 1/3)^2 (1-1/3) = 16/27 \approx 0,593$

Cette valeur est la limite de Betz ! Autrement dit, il n’est pas possible d’extraire plus de 60 % de l’énergie d’un courant d’air. Et pour arriver à ce résultat, il faut avoir $x = 1/3$ soit $v_{av} = \frac{1}{3} v_{am}$.

Les hypothèses du calcul de la limite de Betz

La limite telle qu’on l’a calculée ici tient compte d’un certain nombre d’hypothèses, qui sont les suivantes :

• L’écoulement est incompressible.
• Le flux d’air n’a ni tourbillon, ni turbulence.
• L’éolienne n’a pas de traînée aérodynamique et un nombre infini de pales.

Chaque hypothèse à son importance. L’écoulement incompressible permet d’affirmer que la masse volumique est constante, et donc de simplifier grandement les calculs du débit massique. En plus, la compression et la détente de l’air provoquent des pertes d’énergie, ce qui réduirait la puissance disponible.

L’absence de tourbillon et de turbulence permet de récupérer un maximum d’énergie. En effet, comme le flux est parfaitement droit, l’énergie de l’air est entièrement dédiée à son déplacement utile, de l’avant vers l’arrière de l’éolienne. Les tourbillons, en mettant le flux d’air en rotation, gâchent une partie de l’énergie cinétique disponible. Dans les éoliennes réelles, la rotation des pales fait que le flux d’air à une certaine énergie de rotation en aval.

L’absence de traînée consiste à négliger une partie des pertes présentes dans les éoliennes réelles. Cette hypothèse consiste à affirmer que toute l’énergie de l’air est utilisée pour la mise en rotation de l’éolienne, alors qu’en pratique l’aérodynamisme des pales provoque une force de traînée, qui gâche une partie de l’énergie.

Le nombre infini de pales est également une simplification. Il permet de dire que la poussée du vent est uniforme, et qu’il n’y a pas de vent qui passe à travers la surface de l’éolienne sans être freiné. Le nombre de pales en pratique est évidemment fini ; il y en a généralement trois.

On voit donc qu’il y a un petit nombre d’hypothèses simplificatrices, et qu’elles maximisent le résultat obtenu. Dans la pratique la limite de Betz est ainsi inatteignable, et constitue un majorant plus qu’une véritable limite physique. Certains travaux cherchent d’ailleurs à obtenir un résultat plus proche de la réalité.

Coefficient de puissance maximal atteint en pratique

Malgré toutes les hypothèses simplificatrices, les meilleures éoliennes atteignent déjà des valeurs très respectables pour le coefficient de puissance, comme le montre la figure ci-dessous.

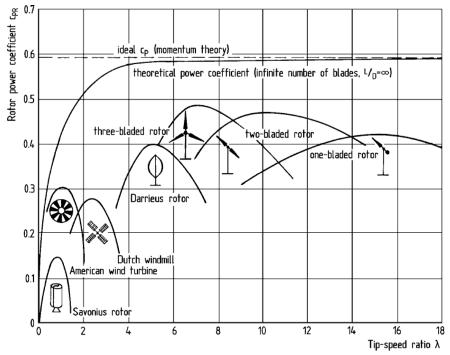
L’abscisse du diagramme est le rapport entre la vitesse de la pointe de l’éolienne et celle du vent incident, qui dépend de comment l’éolienne est contrôlée. Le facteur de puissance varie avec ce paramètre selon une courbe spécifique à chaque modèle d’éolienne.

Les éoliennes courantes, c’est-à-dire à axe horizontal avec trois pales, ont un coefficient de puissance maximal qui atteint presque 0,5 ! Certaines conceptions à quatre pales peuvent être très légèrement meilleures, mais leur coût plus élevé ne justifie pas leur emploi.

Quel vent faut-il pour faire marcher une éolienne de taille moyenne à pleine puissance ?

Maintenant que l’on sait comment se comportent les éoliennes en pratique, faisons quelques petits calculs pour trouver quelle vitesse de vent est nécessaire pour faire marcher à pleine puissance une éolienne de 3 MW. Notre éolienne aura les caractéristiques suivantes (approximativement celles de l'Enercon E-101) :

• $S$ = 8 000 m², sa surface ;
• $P_{t, \, max}$ = 3 MW, sa puissance nominale ;
• $C_{p, \, max}$ = 0,45, son coefficient de puissance, supposé constant ;
• $\rho$ = 1,225 kg/m³, la masse volumique de l’air sur le site d’implantation.

On peut trouver la vitesse du vent grâce à la puissance $P_0$ et cette puissance peut-être exprimée via la définition de $C_p$ :

$P_0 = \frac{P_t}{C_p} = \frac{3}{0{,}45} = 6{,}67~\mathrm{MW}$

Maintenant qu’on connaît la puissance du vent incident, calculons la vitesse correspondante :

$v_{am} = \sqrt[3]{\frac{2 P_0}{\rho \, S}} = 11{,}9~\mathrm{m/s}$

Presque 12 m/s (environ 43 km/h), une sacrée brise ! Ceci montre clairement que les meilleurs emplacements pour les éoliennes sont rares, et qu’il ne faut pas espérer avoir la puissance maximale en permanence…