Tout a fais, d’ailleurs j’aurais dû le préciser directement mais je sais quand même, basiquement, ce qu’est une dérivé, ce quelle représente et à quoi elle sert.
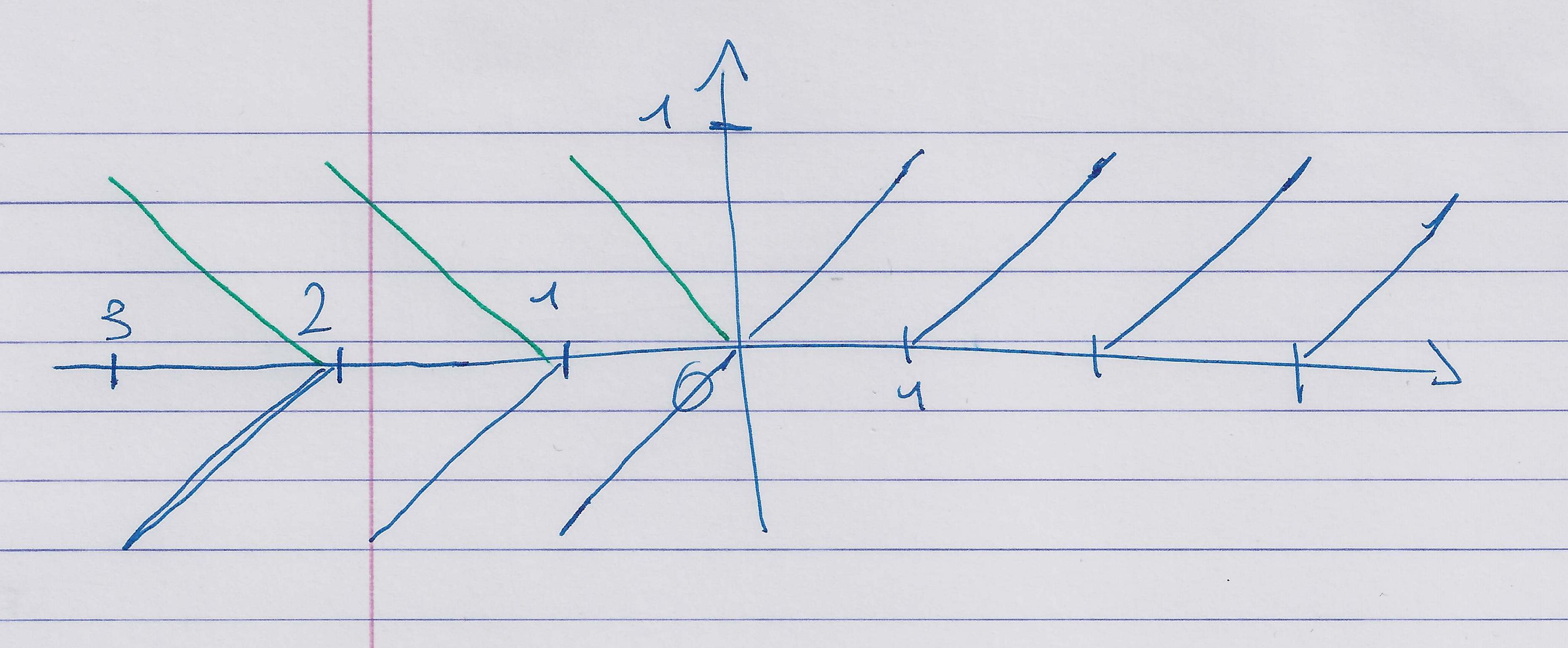
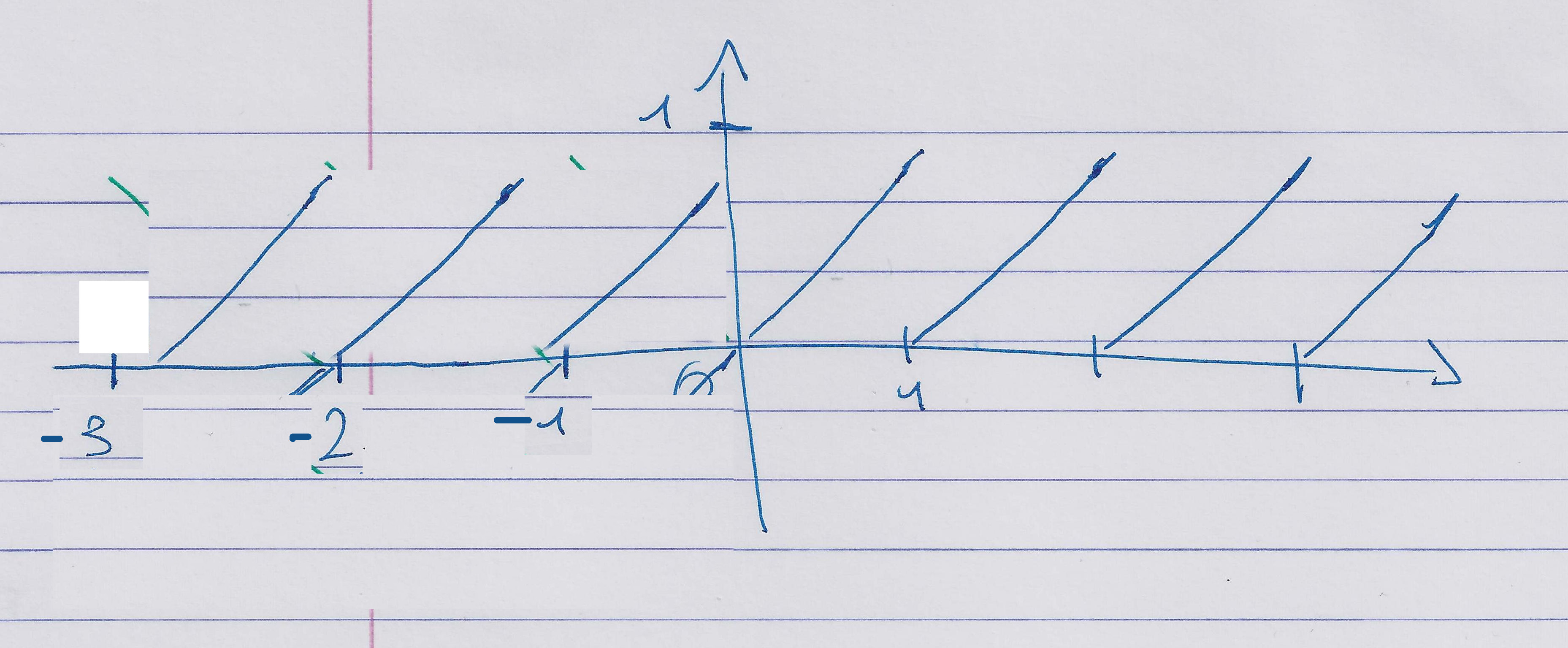
Si tu as une fonction paire qui monte à une certaine vitesse en $1$, alors de l’autre côté, en $-1$, elle va descendre à la même vitesse (soit monter à la vitesse opposée).
C’est plus clair présenté ainsi. 
+0
-0