Pythagore, à quoi ça sert ?

• Aspect mathématique
• Sommaire
• Quelques preuves du théorème

Voilà une phrase que l'on entend souvent, notamment concernant les mathématiques : " A quoi ça me servira dans la vraie vie ? " Même s'il semble étrange de parler de "vraie" vie (comme si les Maths faisaient partie d'une "fausse" vie ) il est tout de même légitime de se poser la question. Quel est l'intérêt de se rentrer dans le crâne des formules mathématiques complexes si elles ne doivent jamais servir ? Alors avant même de commencer à parler géométrie, triangle ou carré, commençons par considérer quelques cas de la "vraie" vie. Nous allons considérer un cas pratique très riche en la matière : la construction d'une maison. Posons-nous deux questions :

1. Comment le maçon ou le charpentier font-ils pour s'assurer que les murs ou les éléments de la charpente sont bien perpendiculaires ?
2. Comment fait l'architecte (ou le maître d’œuvre) pour connaître les dimensions de la toiture d'une maison qui n'existe que sur le papier ? Par exemple la maison ci-dessous :

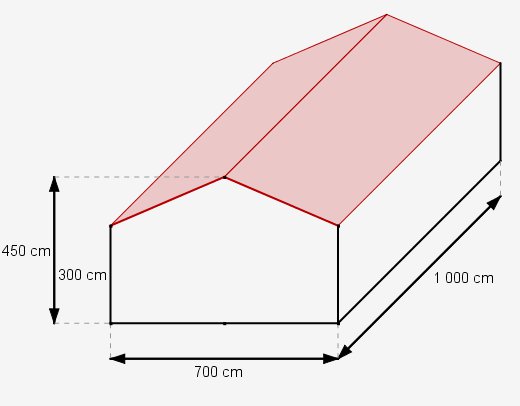
Eh bien, oui ! Avoir une maison de travers, ce n'est pas pratique. L'architecte ne peut se fier qu'à un dessin qui n'est qu'une réduction de la future maison : quelques millimètres d'erreur sur le plan peuvent représenter quelques dizaines de centimètres à l'arrivée. Le maçon et le charpentier n'utilisent évidemment plus leur équerre d'écolier. Et pourtant aucun ne commet d'erreur, avec ou sans outil moderne. Comment font-ils ? Vous voulez la réponse : ils connaissent le théorème de Pythagore et sa réciproque ! Alors, sans plus tarder découvrons-les ensemble.

• Le problème de l'architecte
• Le problème du maçon et du charpentier

Le problème de l'architecte

Élaguons et annotons la figure

Nous pouvons déjà répondre partiellement au problème rencontré par l'architecte : la toiture a une longueur de 1 000 cm soit 10 m. Ce qui nous manque en définitive ce n'est que la largeur d'un pan de toiture (nous supposerons que les deux pans sont symétriques). Finalement, le problème du toit de notre maison en 3 dimensions, peut se ramener à un simple problème en 2 dimensions, un problème de géométrie plane. Nous allons donc simplifier cette figure en ne considérant que le pignon de la maison et nommer les sommets utiles :

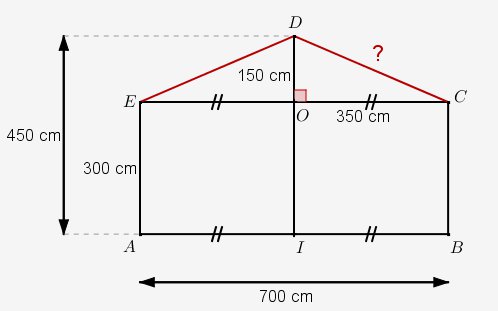
Si notre ami l'architecte a bien travaillé, alors les points I et O de la figure ci-dessus sont les milieux respectifs des segments [AB] et [CE] et donc $AI = IB = EO = OC = {700 \over 2} = 350 cm$. De plus, ABCE doit être un rectangle et les triangles DEO et DOC doivent eux être des triangles rectangles. Enfin, $DO = DI - OI = 450 - 300 = 150 cm$. Le problème revient donc à calculer la longueur de l'hypoténuse du triangle rectangle DOC, connaissant ses cathètes.

Vocabulaire et formulation du théorème

Pardon, je vais un peu vite en besogne. Dans un triangle rectangle, on classe généralement les trois côtés en deux catégories bien distinctes : ceux qui sont accolés à l'angle droit (que l'on appelle cathètes ou plus généralement côtés de l'angle droit) et celui qui ne le touche pas (l'hypoténuse). Vous remarquerez sur la figure ci-dessous que chaque cathète prise séparément est nécessairement plus courte que l'hypoténuse. Certains appuient d'ailleurs sur ce fait en parlant des "petits côtés de l'angle droit", mais cette formulation est redondante.

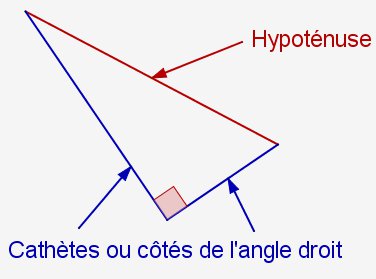
Nous disions donc que pour aider notre ami architecte nous devions trouver la mesure de l'hypoténuse du triangle rectangle COD. Nous connaissons bien les longueurs des deux cathètes CO et DO, mais cela ne nous avance pas d'avantage sur celle de l'hypoténuse CD. Pour y parvenir nous allons avoir recours au théorème de Pythagore dont voici (enfin !) deux formulations :

Avant que vous ne quittiez cette page de dépit, je vais vous expliquer ce théorème plus en détail. Tout d'abord, répondons à la question que vous vous posez peut-être : " C'est quoi ces carrés ? On n'est pas sensé être dans un triangle ? ". Par le mot "carré", les mathématiciens entendent une opération : plus exactement il s'agit de l'opération qui consiste à multiplier un nombre par lui-même. Par exemple, le carré de 5 n'est rien d'autre que la multiplication $5 \times 5 = 25$, que l'on note $5^2 = 25$. Le petit 2 écrit en haut à droite du 5 se lit " au carré " ou " élevé au carré ", comme dans l'unité $cm^2$. Si vous apprenez en ce moment le théorème de Pythagore à l'école, je vous conseille vivement de connaître sur le bout des doigts la liste des carrés de 0 à 15. D'ailleurs en voici une liste qui nous aidera pour la suite :

De la même façon que l'addition a comme opération "contraire" la soustraction ou que l'opération contraire de la multiplication est la division, le carré a une opération contraire appelée la racine carrée et qui se note à l'aide du symbole bizarroïde $\sqrt{\quad}$ voire $\sqrt[2]{\quad}$. Ainsi, chercher la racine carrée de 36, revient à se poser la question : " Quel nombre donne 36 si je le multiplie par lui-même ? ". Vous connaissez la réponse :$\sqrt {36} = 6$ ! Vous souhaitez vous exercer ? En voici quelques autres : calculer $\sqrt {16}$, $\sqrt {4}$, $\sqrt {81}$, $\sqrt {144}$ et $\sqrt {225}$. Vous pourrez vous aider de la liste de valeurs ci-dessus et lorsque vous aurez fini, vous pourrez cliquer ci-dessous pour connaître les réponses.

Retour sur les plans de l'architecte

Maintenant que vous disposez du vocabulaire, du théorème et des opérations nécessaires, il est temps de mettre tout cela en application. Le théorème de Pythagore nous dit que l'on peut calculer le carré de l'hypoténuse en additionnant les carrés des deux cathètes. Commençons donc par calculer ces fameux carrés : $DO^2 = 150^2 = 22\;500$ et $CO^2 = 350^2 = 122\;500$.

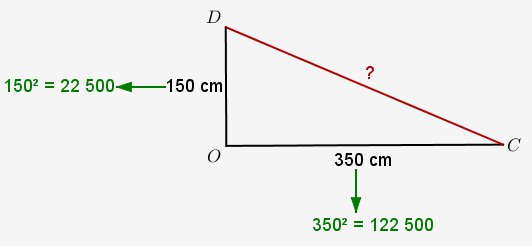
Additionnons maintenant les résultats obtenus :

Attention ! Le résultat obtenu n'est pas la longueur de l'hypoténuse mais son carré. Il nous reste donc une dernière étape : obtenir l'hypoténuse sachant que c'est un nombre dont le carré vaut 145 000. Comment obtenir un tel nombre ? Eh bien grâce à la racine carrée (une bonne vieille calculatrice fera l'affaire car pour ma part je ne connais pas toutes les racines carrées possibles et imaginables) :

Renversons le problème

Si l'on ne connaît qu'un seul côté du triangle, le théorème de Pythagore est inopérant, il faut bien l'admettre. Toutefois, imaginons que notre architecte ne connaisse que la largeur de la maison (toujours 350 cm) mais que les pentes de toiture réglementaires lui imposent qu'un pan de toit mesure 400 cm de longueur. Nous aboutissons alors à la figure suivante :

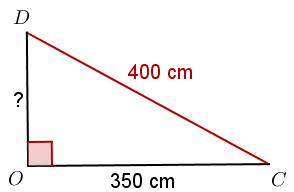
Cette fois, nous connaissons une seule cathète et l'hypoténuse. Mais nous pouvons toujours appliquer le théorème de Pythagore. Commençons par calculer les carrés des côtés connus : $DC^2 = 400^2 = 160\;000$ et $OC^2 = 350^2 = 122\;500$. Le théorème de Pythagore nous donne alors l'égalité suivante :

Comment trouver $OD^2$ ? Si en lui ajoutant 122 500, on trouve 160 000 alors il suffit de soustraire 122 500 à 160 000 pour trouver sa valeur :

Le problème du maçon et du charpentier

En effet, cette technique est valable pour un architecte qui conçoit ses plans en intérieur, derrière sa table de dessin, mais elle devient un peu trop compliquée pour quelqu'un travaillant en extérieur sur un chantier. Il faut une technique encore plus rapide et efficace. Heureusement pour nous, le théorème de Pythagore vient à nouveau à notre secours, ou plutôt sa réciproque.

Réciproque et contraposée du théorème de Pythagore

Et voilà encore un nouveau mot : réciproque. Qu'est-ce encore que cela ? C'est simple, on parle de propriété réciproque lorsque l'on formule une propriété en sens inverse. Par exemple, si l'on considère le dicton " Lorsqu'il fait nuit, tous les chats sont gris ", le dicton réciproque serait " Lorsque tous les chats sont gris, il fait nuit ".

Eh bien non justement ! Une propriété mathématique peut-être vraie et avoir une réciproque fausse. La propriété réciproque est une nouvelle propriété à part entière. Prenons un exemple simple : " Si mon ballon est un ballon de foot, alors il est rond ". Quoi de plus logique ? La réciproque de cette phrase serait : " Si mon ballon est rond, alors c'est un ballon de foot ". Aïe ! Cette dernière phrase n'est pas vraie : pour s'en convaincre il suffit de se rappeler que les ballons de hand ball, de basket ou de volley sont ronds eux aussi. Mais heureusement pour nous, le théorème de Pythagore a une réciproque qui fonctionne et dont voici l'énoncé (je vous invite à essayer de le formuler vous-même avant de le lire) :

Vous remarquerez que je ne parle plus d'hypoténuse ou de cathètes. Et pour cause, au début de l'énoncé, nous considérons un triangle quelconque vérifiant seulement une égalité particulière. Ce n'est qu'à la toute fin de la propriété que l'on découvre qu'il est rectangle et que l'on peut donc parler d'hypoténuse et cathètes. Enfin, que nous dit cette fameuse réciproque ? Elle nous dit que si l'on connaît les trois côtés d'un triangle et qu'en les élevant tous les trois au carré et en additionnant les deux plus petits, on trouve la valeur du carré du plus grand, alors on peut être certain que ce triangle est rectangle. C'est donc ce principe que notre maçon va devoir utiliser. Reste seulement à trouver trois longueurs vérifiant la réciproque de Pythagore et qui soient faciles à retenir.

Mais avant cela il reste une question en suspens : et si un triangle ne vérifie pas l'égalité de Pythagore, est-on certain qu'il n'est pas rectangle ou existe-t-il des cas particuliers qui seraient tout de même rectangles ? Ça, la réciproque ne le dit pas. Mais ce genre de cas particulier est impossible car il contreviendrait au Théorème de Pythagore lui-même. Supposons qu'il existe un triangle ne vérifiant pas l'égalité mais qui serait tout de même rectangle : le fait qu'il soit rectangle nous permettrait alors d'utiliser le théorème de Pythagore qui nous assurerait qu'il vérifie l'égalité, ce qui est en contradiction avec l'hypothèse initiale. Pour être plus clair encore, on peut formuler la propriété suivante :

Cette troisième propriété est ce que l'on appelle la Contraposée du théorème de Pythagore. La contraposée d'une propriété n'est rien d'autre que la même propriété, formulée de manière négative. Par exemple, la propriété " Si j'ai 35 ans alors je suis majeur " peut se reformuler ainsi : " Si je ne suis pas majeur alors je ne peux pas avoir 35 ans ". Par conséquent, la contraposée d'un théorème est obligatoirement vraie car équivalente au théorème lui-même.

Résolution du problème du maçon

Mais revenons-en à nos maçons. Euh … nos moutons ! Comment peut-on s'assurer que deux murs sont biens perpendiculaires à l'aide de la réciproque ou de la contraposée de Pythagore ? Pour cela, nous devons au préalable trouver trois longueurs vérifiant l'égalité de Pythagore et qui soient des nombres entiers de préférence. C'est ce que l'on appelle un triplet pythagoricien, et il en existe une infinité. A vous de jouer !

Vous n'en trouvez pas ? Alors lisez bien cette vieille astuce d'artisan. Notre maçon va devoir se placer à l'intersection des deux murs (dans le coin, quoi). A l'aide de son mètre, il devra mesurer 3m le long du premier mur et faire une marque au sol (à la craie ou à la bombe de peinture). Puis il recommencera sur le second mur en mesurant cette fois 4m. Si les deux murs sont bien perpendiculaires, alors il devrait mesurer 5m d'écart entre ses deux marques. Vous voulez une preuve ?

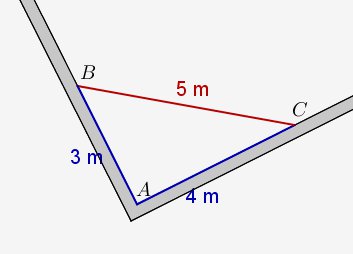
Avec les notations de la figure, calculons la somme des carrés des deux petits côtés :

Et maintenant, passons au carré du plus grand côté : $BC^2 = 5^2 = 25$.

On constate bien que $BC^2 = AB^2 + AC^2$ et d'après la réciproque de Pythagore, le triangle ABC est bien rectangle. Le triplet pythagoricien 3/4/5 est le plus simple de tous, c'est pourquoi il est souvent utilisé. Certains charpentiers utilisent quant à eux le triplet 6/8/10 qui n'est rien d'autre que le double du précédent. Pratique, non ?

A retenir

• Théorème de Pythagore : Si un triangle est rectangle, alors le carré de son hypoténuse est égal à la somme des carrés des deux autres côtés.
• Le théorème de Pythagore est un puissant outil permettant de calculer une longueur manquante dans un triangle rectangle.
• Réciproque du Théorème : Si le carré du plus grand côté d'un triangle est égal à la somme des carrés des deux autres côtés, alors ce triangle est rectangle.
• La réciproque du théorème de Pythagore permet de s'assurer qu'un triangle est rectangle.

• Aspect mathématique
• Sommaire
• Quelques preuves du théorème