Pythagore n'a jamais découvert son propre théorème ! Ce serait un usurpateur ? Mais alors qui est le véritable inventeur du théorème qui porte son nom ?
Pour être honnête avec vous, nous ne connaissons pas le découvreur du théorème de Pythagore, pour une raison bien simple : il s'agit d'une propriété connue depuis des millénaires. Nous savons par exemple que les Babyloniens la connaissaient un millénaire avant la naissance de Pythagore. Les babyloniens, vous connaissez ? Non ? Et si je vous parle de Babel et de sa tour, ça vous dit quelque chose ? Eh bien, Babel n'est rien de plus que le nom hébraïque d'une très ancienne et très puissante cité connue sous le nom de Babylone. Nous allons d'ailleurs y faire une petite escale avant de retrouver Pythagore et la Grèce.
La mythique Babylone
La civilisation babylonienne
La cité de Babylone aurait été fondée au cours du IIIème millénaire avant Jésus Christ aux environs de l'actuelle Bagdad, en Mésopotamie (grosso modo l'Iraq actuel). Pour vous donner un ordre d'idée, à cette période l’Égypte construit la grande pyramide de Kheops et les Grecs en sont encore à l'âge du bronze et essayent de coloniser le pays (bref, ils sont plus proches des Pierrafeu que d'Aristote). Babylone, bien que construite tardivement au beau milieu d'une région déjà très urbanisée et développée pour l'époque, va prendre un essor inattendu et devenir rapidement la première puissance régionale. Après des hauts et des bas, Babylone formera même au VIIème siècle av.JC. un empire s'étendant sur tout le moyen-orient :

Si la civilisation babylonienne est moins bien connue du grand public que la civilisation égyptienne, il ne faut pas pour autant la dénigrer. Ses prouesses architecturales ou scientifiques n'ont rien à envier au pays du Nil. Côté architecture, Babylone hébergeait l'une des sept merveilles du monde antique : les jardins suspendus (aujourd'hui disparus) ; ses gigantesques murailles ainsi que ses portes monumentales (comme la porte d'Ishtar) étaient connues des grecs eux-mêmes ; enfin, les civilisations mésopotamiennes étaient réputées pour leurs ziggurat, d'immenses temples rappelant les pyramides égyptiennes. D'ailleurs, la ziggurat de Babylone a marqué les mémoires puisque c'est elle que la Bible nomme Tour de Babel.



Babylone est également connue pour la production d'un des premiers et plus célèbres codes de loi : le code de Hammurabi. Mais, pour ce qui nous concerne, Babylone devint surtout un grand centre scientifique. Si vous en doutez, sachez que les Babyloniens comptaient en base 60, c'est à dire avec 60 chiffres quand nous n'en avons que 10 (enfin presque, il n'en avaient que 59 puisqu'il leur manquait le zéro). Et que c'est à cause de cette tradition que nous comptons 60 secondes dans une minute, 3600 dans une heure ou deux fois 12 heures dans une journée. C'est également aux Babyloniens que nous devons nos degrés pour mesurer les angles : en bons astronomes, ils partagèrent la voûte céleste en 6 secteurs de 60° chacun, d'où $6 \times 60 = 360°$, comme les 360 jours de l'année (presque, c'était 365,25 mais ce n'était pas si mal pour l'époque). D'où notre habitude de mesurer des angles droits de 90°, des angles plats de 180° et des angles pleins de 360°. Férus d'astrologie, ils étudièrent le ciel comme peu de civilisations ne le firent. Ils constatèrent le caractère cyclique de nombreux phénomènes astronomiques et développèrent ce que l'on nomme aujourd'hui la trigonométrie, le cosinus, le sinus …
La tablette Plimton 322
De nombreuses tablettes d'argile attestent de ces connaissances poussées sur les mesures du triangle (ce que l'on nomme la trigonométrie). Mais une en particulier va retenir notre attention, une tablette répondant au doux nom de Plimpton 322.

Cette tablette, aujourd'hui conservée à l'université de Columbia, daterait de -1800. Elle est incomplète mais comporte suffisamment d'informations pour vous faire douter de Monsieur Pythagore. Elle comporte des listes de nombres présentés par lignes, à la façon d'un manuel de mathématiques présentant des listes d'exercices types. Et parmi ces nombres, on découvre notamment des triplets pythagoriciens. Mais attention ! Il ne s'agit pas de triplet du genre 3/4/5 ou 6/8/10, non ! Ces triplets sont bien plus compliqués : le premier d'entre eux est 119, 120, 169 !  Vérifions ensemble :
Vérifions ensemble :
La réciproque du théorème de Pythagore est vérifiée : ces longueurs donnent bien un triangle rectangle. Et si le calcul du carré de 169 ne vous a pas découragé, voici un second triplet de la tablette : 4961, 6480, 8161 ! Ce simple exemple nous montre que les Babyloniens avaient une parfaite connaissance de l'égalité de Pythagore et, de plus, qu'ils disposaient d'algorithmes efficaces pour calculer les racines carrées. Pour les plus curieux et les plus chevronnés, je vous présente dans la bannière cachée la méthode dite babylonienne permettant d'extraire une racine carrée.
Ce qui suit exige une certaine technicité et une bonne dose de calcul mental.
Vous vous êtes peut-être déjà demandé comment extraire une racine carrée à la main ? Eh bien c'est faisable grâce à la méthode babylonienne que je vais dérouler ici avec le nombre 28 561 dont nous avons vu que la racine carrée était 169. Tout d'abord, on pose le calcul de racine à la manière d'une division, avec une potence (voir ci-dessous). Écrivons le nombre 28 561 en haut à gauche en prenant soin d'ajouter un zéro devant pour avoir un nombre pair de chiffres. On sélectionne ensuite les deux premiers chiffres (ici 02) et on cherche le nombre dont le carré est le plus proche de 2 tout en lui étant inférieur ou égal. Ici, c'est 1 car $1^2 = 1$ alors que $2^2 = 4 > 2$. On écrit donc 1 en haut à droite et le résultat de $1^2$ en dessous de 2 et on effectue la soustraction $2 - 1 = 1$ :
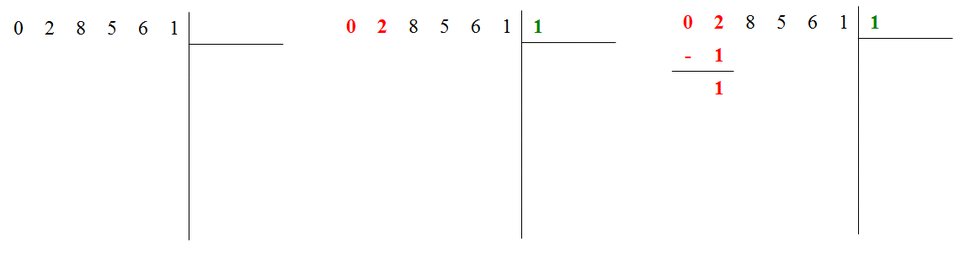
Jusque là, pas de problème. Ça ressemble beaucoup à la division. C'est maintenant que tout se complique. Abaissons deux chiffres supplémentaires : on obtient 185. Et là, il ne faut pas chercher un carré proche de 185, ce serait trop simple. Il faut revenir à notre résultat précédent (le 1) et le multiplier par 2. On écrit le résultat en dessous (partie en bas à droite) et on cherche un chiffre a tel que $2a \times a$ soit le plus proche possible de 185 tout en lui restant inférieur ou égal. Par exemple, $2 \color{red} 5 \color{black} \times \color{red} 5 \color{black} = 125$ est inférieur à 185, mais on doit pouvoir trouver mieux. $2 \color{red} 7 \color{black} \times \color{red} 7 \color{black} = 189$ est plus grand que 185, le nombre cherché est donc 6 car $2 \color{red} 6 \color{black} \times \color{red} 6 \color{black} = 156$ . On écrit donc 6 en haut à droite et on effectue la soustraction $185 - 156 = 29$ .

Ardu n'est-ce pas ? Si vous avez compris, l'étape suivante sera identique : on abaisse deux chiffres à gauche pour obtenir 2961, à droite on double le résultat pour obtenir $16 \times 2 = 32$ et on cherche à nouveau un chiffre a tel que $32a \times a$ soit le plus proche de 2961 tout en lui étant inférieur ou égal. Ce chiffre est 9 car $32 \color{red} 9 \color{black} \times \color{red} 9 \color{black} = 2961$ . On place 9 en haut à droite et on effectue la soustraction $2961 - 2961 = 0$ . Opération terminée : $\sqrt {28 561} = 169$ .

Revenons à notre tablette Plimpton 322. Elle prouve que les Babyloniens avaient une grande maîtrise de la formule de Pythagore, mais ce n'est pas tout. Si l'on considère la colonne de gauche, on voit apparaître des nombres bien plus longs. Ces nombres donne la valeur de l'opération suivante :
La division $hypoténuse \over cathète$ donne ce que l'on appelle aujourd'hui la sécante ou la cosécante des angles du triangle rectangle, c'est à dire l'inverse du cosinus ou du sinus de l'angle. Si vous ne connaissez pas encore le cosinus ou le sinus, sachez qu'il s'agit d'un outil géométrique particulièrement complexe et puissant qui a en plus l'avantage d'avoir des valeurs qui ne tombent presque jamais juste. 
Pendant ce temps en Égypte
Le papyrus Rhind
Il ne fait donc aucun doute que le théorème de Pythagore était connu des Babyloniens presque 2000 ans avant notre ère, mais surtout plus de 1000 ans avant Pythagore lui-même. Mais qu'en était-il des Égyptiens (je ne vous présente bien entendu pas cette brillante et célèbre civilisation) ? Eh bien, côté Égyptien c'est le flou. En fait, on est quasiment certain que le théorème était connu et maîtrisé mais il n'existe pas pour l'heure de preuve flagrante. Il existe bien des papyrus de Mathématiques comme le papyrus Rhind ou le papyrus de Moscou qui présentent des calculs de longueur, d'aire ou de volume particulièrement complexes. On y trouve le théorème de Thalès, mais pas celui de Pythagore.

Mais alors qu'est-ce qui nous faire croire que les Égyptiens maîtrisaient le théorème de Pythagore ?
Pour plusieurs raisons. Tout d'abord, le papyrus Rhind traite régulièrement des problèmes de pente de pyramide. La pente d'un triangle rectangle indique l'inclinaison de son hypoténuse et n'est autre que la tangente d'un des angles aigus du triangle ou, plus simplement, la division d'une des cathètes par la seconde. Par exemple, pour un triangle 3/4/5, la pente correspond à la fraction $4 \over 3$ ou à la fraction $3 \over 4$ (cela dépend de l'orientation du triangle). Or, c'est cette même pente qui est utilisée la plupart du temps dans le papyrus. Jamais le théorème de Pythagore n'est utilisé en tant que tel, mais le triplet pythagoricien 3/4/5 est utilisé presque partout sans jamais le dire. D'ailleurs, certaines pyramides sont construites dans des proportions très proches du triplet 3/4/5. C'est pourquoi ce fameux triplet est parfois appelé triangle égyptien.
Le don du Nil
Une autre raison tient à la nature même de l’Égypte. Il s'agit avant tout d'un pays agricole vivant au rythme du Nil. Tous les ans le grand fleuve sort de son lit et recouvre les champs, les fertilisant de ses alluvions. Problème : une fois la décrue amorcée, comment savoir où se situaient les canaux et les limites de parcelles ? Le pouvoir de délimiter les parcelles au nom du pharaon était attribué à des géomètres ou arpenteurs. Ces derniers se retrouvaient inévitablement dans la même situation que le maçon de l'exemple précédent : comment réaliser une figure géométrique de base comme la droite, le cercle ou l'angle droit pour partager les terres ? (Ceux qui répondent " avec un télémètre laser " ont du manquer une étape  ).
).
La réponse est bien plus simple qu'il n'y paraît : à l'aide d'une corde ! Pour tracer une droite, il suffira de la tendre. Pour tracer un cercle ou juste un arc de cercle, il suffira de fixer une extrémité de la corde à un piquet et de se déplacer en conservant la corde tendue. C'est ainsi que les anciens ont imaginer mille et une construction "à la règle non graduée et au compas" pour obtenir des milieux, des triangles, des bissectrices … Quant à l'angle droit, il suffit de reprendre à nouveau le triangle égyptien 3/4/5. Pour cela, l'arpenteur réalisait un nœuds à l'une des extrémités de la corde puis un second un peu plus loin. Ensuite, il reportait la distance entre les deux nœuds tout le long de la corde afin d'obtenir 13 nœuds en tout. Pourquoi 13 nœuds ? Eh bien car entre 13 nœuds, on compte 12 intervalles et que $3+4+5 = 12$ ! Il devenait donc possible de réaliser le fameux triangle égyptien et ainsi de construire un angle droit en reliant entre eux le premier et le dernier noeuds.
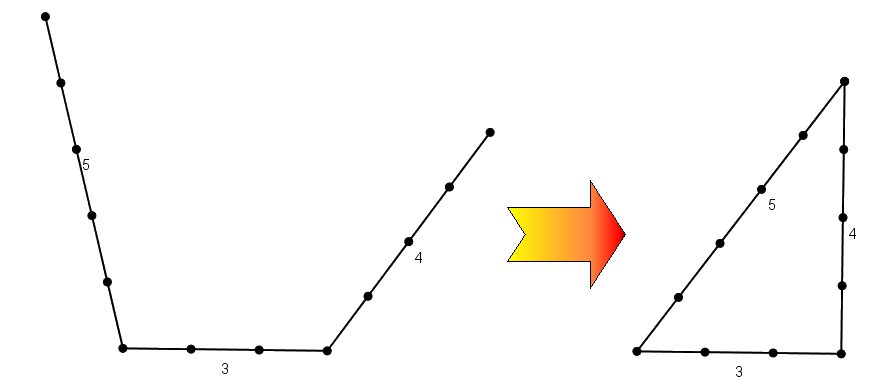
Cette technique, rudimentaire mais efficace sera utilisée pendant des millénaires.
A retenir
- Le théorème de Pythagore est une très ancienne propriété géométrique apparue plus d'un millénaire avant Pythagore lui-même.
- Les Grecs n'ont pas inventé les Mathématiques : la plupart de leurs connaissances sont issues d’Égypte et de Mésopotamie.
- Le triangle égyptien de longueurs 3/4/5 est un triangle rectangle