Nous savons désormais que le théorème de Pythagore ne s'applique que dans un triangle rectangle. Oui mais des triangles rectangles, on peut en trouver dans bien des figures géométriques, il suffit d'un angle droit, d'une hauteur ou d'une médiatrice. Par conséquent, notre cher théorème va nous permettre de calculer des longueurs inconnues, que ce soit dans des rectangles, des cubes ou des triangles non rectangles. Je vous propose ici un assortiment d'exercices de difficultés variables dont les solutions seront réutilisées dans le prochain chapitre. Chaque partie commence par un exercice accessible aux débutants et ouvrant la voie au second exercice, plus complexe ou nécessitant des connaissances en algèbre.
Diagonales de rectangles et de carrés
Diagonale du rectangle
Énoncé
Quelle est la longueur de la diagonale d'un rectangle de largeur 8 cm et de longueur 15 cm ?
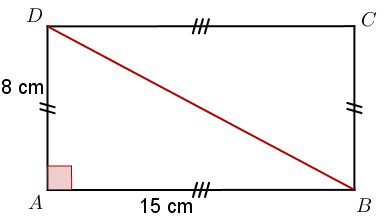
Solution
Cet exercice est le plus simple de tous. En traçant la diagonale [BD], on fait apparaître deux triangles rectangles. Il suffit donc de se placer dans l'un des deux, par exemple ABD. Le théorème de Pythagore donne ainsi :
Diagonale du carré
Énoncé
Quelle est la longueur de la diagonale d'un carré de côté $a$ ?
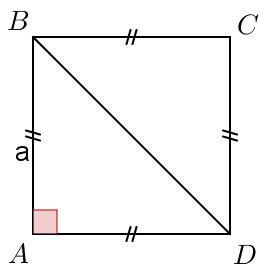
Solution
Il suffit là encore de tracer une diagonale pour qu'un carré soit partagé en deux triangles rectangles. Il est donc possible d'appliquer le théorème de Pythagore. La difficulté réside ici dans l'utilisation non plus d'un nombre connu mais d'une lettre $a$ symbolisant n'importe quel nombre positif. Fions-nous au travail effectué précédemment :
Nous arrivons à un résultat bizarroïde et incalculable : $\sqrt{2 a^2}$. Toutefois, il est possible d'améliorer l'écriture de ce résultat grâce à une propriété des racines carrées. Prenons un exemple. On sait que $\sqrt 36 = 6$ mais on sait aussi que $36 = 9 \times 4$. Or $\sqrt 9 \times \sqrt 4 = 3 \times 2 = 6$ donc on peut écrire que $\sqrt{9 \times 4} = \sqrt 9 \times \sqrt 4$. Plus généralement :
$\sqrt{x \times y} = \sqrt x \times \sqrt y$, avec $x$ et $y$ positifs ou nuls.
Attention, cette propriété fonctionne avec la multiplication, mais pas avec l'addition ou la soustraction. Un contrexemple suffira à s'en convaincre. On sait que $\sqrt 25 = 5$. Mais 25 peut se décomposer en 16 + 9. Or, $\sqrt 16 + \sqrt 9 = 4 + 3 = 7 \neq 5$.
Revenons à notre carré de côté $a$. Nous avons écrit que sa diagonale mesurait $\sqrt{2 a^2}$, ce qui peut s'affiner :
Autrement dit, si l'on connaît le côté d'un carré, il suffit de multiplier par $\sqrt 2$ pour connaître sa diagonale.
La duplication du carré
Cette propriété permet de résoudre un antique problème, celui de la duplication du carré. Le but de ce problème est de construire à la règle non graduée et au compas, un carré dont l'aire est exactement le double de celle d'un carré donné. Il n'est pas question de mesurer les longueurs ou les angles ! Vous ne pouvez faire que des droites et des cercles.
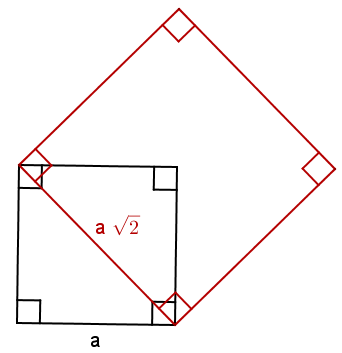
La solution est maintenant simple. Pour un carré de côté $a$, l'aire vaut $a \times a = a^2$. En construisant comme ci-dessus un carré le long de sa diagonale, on obtient un côté de longueur $a \sqrt 2$ et une aire de $a \sqrt 2 \times a \sqrt 2$. Cependant :
Le carré obtenu a donc une aire double du premier.
Diagonales de pavés et de cubes
Passons désormais aux figures en 3 dimensions, les solides. Les deux exercices que je vous propose ressemblent beaucoup à ceux déjà effectués avec le rectangle et le carré.
Diagonale du parallélépipède rectangle
Énoncé
Quelle est la longueur de la diagonale d'un parallélépipède rectangle de dimensions 3 cm / 4 cm / 12 cm ?
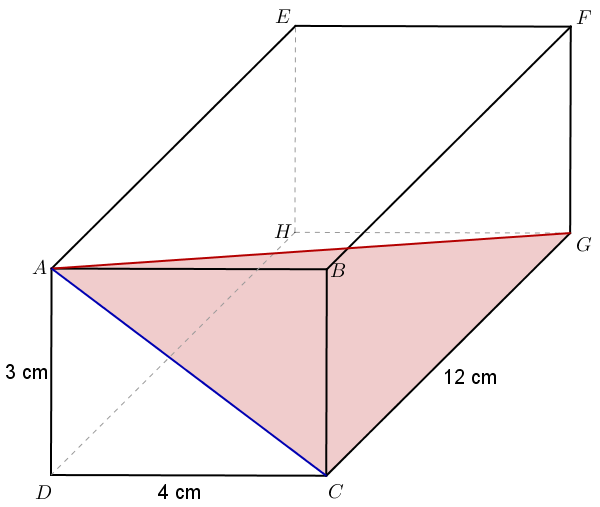
Solution
Avant de calculer AG, il est important de faire apparaître un triangle rectangle dont [AG] est un côté. Nous allons prendre ici le triangle ACG. Mais nous avons un soucis : nous ne connaissons qu'un seul de ses côtés. Qu'à cela ne tienne : nous allons d'abord calculer un second côté de ACG. Pour cela nous devons trouver un deuxième triangle rectangle ayant [AC] pour côté.
Prenons par exemple le triangle ADC rectangle en D. Ses cathètes mesurent 3 cm et 4 cm. Vous devriez déjà avoir repéré le fameux triplet pythagoricien 3/4/5 dont nous avons déjà parlé lors du problème du maçon. Je vous fais donc grâce de ces calculs.
Nous pouvons enfin en revenir au triangle ACG dont nous connaissons désormais les cathètes : AC = 5 cm et CG = 12 cm. Le théorème de Pythagore nous donne alors :
Diagonale du cube
Énoncé
Déterminer la longueur de la diagonale d'un cube d'arête $a$.
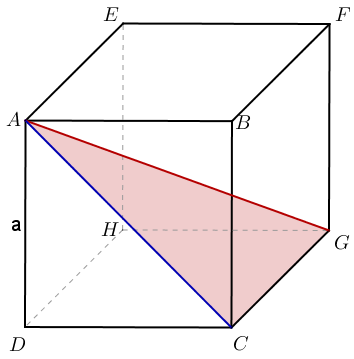
Solution
Le raisonnement à suivre est ici le même que durant l'exercice du parallélépipède rectangle :
- calculer d'abord AC avec le théorème de Pythagore dans le triangle ADC,
- en déduire ensuite AG en utilisant le triangle ACG.
Mais rappelez-vous l'exercice sur la diagonale du carré : nous savons déjà qu'un carré de côté $a$ dispose d'une diagonale de longueur $a \sqrt 2$. Nous pouvons donc en déduire sans plus de cérémonie que $AC = a \sqrt 2$. Reste donc seulement le calcul de AG :
Nous appliquons alors la même simplification que lors du calcul de la diagonale du carré :
Nous arrivons donc à ce résultat intéressant que la diagonale d'un carré de côté $a$ vaut $a \sqrt 2$, que la diagonale d'un cube d'arête $a$ vaut $a \sqrt 3$.
Nous pourrions même élargir cette propriété à des espaces ayant plus que 3 dimensions. Même si ces espaces sont difficiles à visualiser, rien ne nous empêche d'imaginer des espaces à 4, 5, 6 dimensions ou plus encore. L'équivalent du carré et du cube dans un espace à 4 dimensions se nomme alors hypercube, l'équivalent du cercle ou de la sphère se nommer hypersphère etc. Ainsi, avec une 4ème dimension, la diagonale d'un hypercube à 4 dimensions et d'arête $a$ vaudrait $a \sqrt 4 = 2 a$, alors qu'avec une 5ème dimension elle vaudrait $a \sqrt 5$…
Duplication du cube
Comme pour le carré, nous en venons donc au problème de la duplication du cube :
Un cube étant donné, construire à la règle non graduée et au compas un cube dont le volume sera le double du premier.
Vus les résultats obtenus pour le carré et le cheminement très similaire de nos réflexions en 2D et en 3D, vous devriez déjà avoir une idée. Il suffirait de tracer la diagonale du premier cube (dont le volume est $a \times a \times a = a^3$) puis de construire un cube reposant sur ladite diagonale. Comme celle-ci mesure $a \sqrt 3$, le volume du cube obtenu sera :
Et c'est là que ça coïnce ! Le cube obtenu a un volume non pas 2 fois mais $3 \sqrt 3$ fois plus grand. Avec la diagonale d'une des faces carrées du cube, peut-être ? Hélas, le cube obtenu aurait un volume $2 \sqrt 2$ fois plus grand. C'est mieux, mais toujours insuffisant. Allez, je vous laisse réfléchir par vous-même. La solution n'est en fait pas si compliquée.
Alors, vous n'avez pas trouvé ? Vous voulez la solution ? C'est simple : ce problème est insoluble. 
Posé au cours du VIème siècle avant notre ère, il aura fallu attendre le XIXème pour connaître la réponse. Ce problème fait partie des trois grands problèmes antiques, trois problèmes de construction à la règle et au compas qui donnèrent tant de maux de tête aux géomètres et mathématiciens. Parmi ces trois grands problèmes antiques, on trouve également la trisection d'un angle (son partage en trois parts égales) et la célèbre quadrature du cercle (construction d'un carré de même aire qu'un disque). A ces trois grands problèmes, j'aime en ajouter un quatrième : le 5ème postulat d'Euclide, propriété élémentaire indémontrable de la géométrie.
Hauteur d'un triangle
Hauteur d'un triangle isocèle
Énoncé
Dans un triangle isocèle de base 10 cm et dont les deux autres côtés mesurent 13 cm, calculer la hauteur relative à la base.
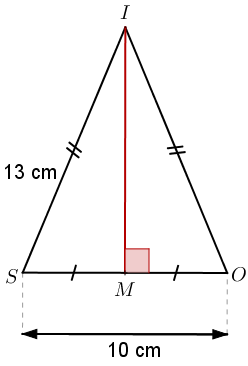
Solution
Il s'agit ici de calculer la longueur IM. Le triangle étant isocèle, la hauteur (IM) partage le triangle en deux triangles rectangles de mêmes longueurs. On trouve que $MS = 10 \div 2 = 5 cm$. On peut donc utiliser le théorème de Pythagore dans le triangle IMS par exemple. Mais attention, on connaît cette fois l'hypoténuse du triangle. Ce que l'on cherche, c'est l'un des cathètes.
Hauteur d'un triangle équilatéral
Énoncé
Quelle est la hauteur d'un triangle équilatéral de côté 1 cm ?
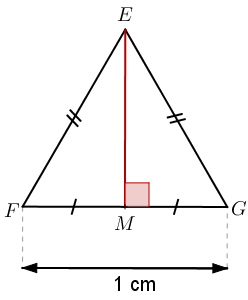
Solution
Contrairement à la diagonale du carré, j'ai décidé ici de vous épargner. Le côté du triangle équilatéral n'est pas une inconnu, mais un nombre très simple : 1. La logique est ici la même que pour le triangle isocèle : le triangle EFM est rectangle en M, son hypoténuse mesure 1 cm et $FM = {1 \over 2} cm$. Reprenons le calcul précédent :
Nous utilisons ici une autre propriété des racines carrées :
$\sqrt {x \over y} = {\sqrt x \over \sqrt y}$, avec $x$ positif et $y$ strictement positif.
A retenir :
- La diagonale d'un carré de côté $a$ vaut $a \sqrt 2$
- La diagonale d'un cube d'arête $a$ vaut $a \sqrt 3$
- La hauteur d'un triangle équilatéral de côté 1 vaut ${\sqrt 3}\over 2$
- La duplication d'un cube à la règle et au compas est impossible