Les équations

Aimez-vous les devinettes ? Si la réponse est oui, alors vous allez adorer les équations !

Les équations font souvent très peur quand on les apprend à l’école, et pourtant ce ne sont rien d’autres que des petites énigmes qui peuvent se révéler passionnantes à résoudre. Si on les prend par le bon bout et en connaissant les astuces qui existent pour venir à bout de leurs secrets, les équations peuvent devenir un jeu d’enfant !

Ce cours est précisément là pour ça ! Que vous cherchiez à comprendre votre cours et à réviser votre prochain contrôle ou que vous soyez juste là pour le plaisir de faire des maths, vous trouverez ici tout ce qu’il vous faut. Nous allons repartir de zéro en commençant par expliquer ce qu’est une équation, puis nous verrons pas à pas les différents types d’équations et les méthodes qui existent pour les résoudre.

Vous êtes prêts ? Alors partons ensembles sur la piste de ces mystérieuses inconnues…

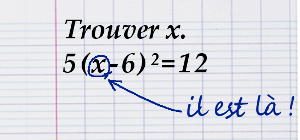
Présentation des équations

1. Qu'est-ce qu'une équation ?

   1. Qu'est-ce qu'une équation ?

   2. L'algèbre rhétorique

   3. Un langage pour les équations

2. Premières manipulations d'équations

   1. Remonter vers l'inconnue

   2. Transformons les équations

   3. Toutes les équations valent zéro

   4. Les équations par degré

3. TP : Inventons des équations !

   1. Avec une solution

   2. Avec deux solutions

   3. Multiplions les solutions

Équations à une inconnue

1. Équations du premier degré

   1. La résolution

   2. Quelques énigmes

   3. Représentation graphique

2. Équations du second degré

   1. La forme canonique

   2. La forme factorisée

   3. Quelques énigmes

   4. Représentation graphique

3. Équations de degré supérieur

   1. Une polémique en Italie

   2. Deux grands théorèmes

4. Équations non polynomiales

   1. Racines

   2. Exponentielles et logarithmes

   3. Fonctions trigonométriques

   4. Un exemple

5. Méthodes de résolution numérique

   1. Tableaux de variations

   2. Méthode de dichotomie

   3. Méthode de la fausse position

Équations à plusieurs inconnues

1. Équations à deux inconnues

   1. Représentation des solutions

   2. Méthodes de résolution

   3. Équations polynomiales

   4. Système d'équations

2. De plus en plus d'inconnues

   1. Représentation des solutions

   2. Équations du premier degré

   3. Méthodes de résolution

Annexes

1. Inéquations

   1. Plus grand ou plus petit

   2. Méthode de résolution

Voilà, ce cours est maintenant terminé ! Si vous avez des remarques ou des questions à propos de celui-ci, n’hésitez pas à les poser dans les commentaires. Pour des questions plus générales sur les équations, vous pouvez également utiliser le forum Science de Zeste de Savoir.

Références

Voici la liste des documents/livres que j’ai consultés lors de l’écriture de ce cours, par ordre alphabétique de leurs auteurs.

• Tablette BM 13901 - Anonyme - XVIIIe siècle av. J.-C.
• Abrégé du calcul par la restauration et la comparaison (الكتاب المختصر في حساب الجبر والمقابلة) - M. Al-Khawarizmi - 833
• A History Of Mathematical Notations - Vol I: Notations In Elementary Mathematics - F. Cajori - The open court company - 1928
• Ars Magna - G. Cardano - 1545
• The book of Numbers - J. H. Conway et R. K. Guy - Copernicus books - 1996
• Des mathématiciens de A à Z - B. Hauchecorne et D. Surreau - Ellipses - 1996
• L’algèbre au temps de Babylone - J. Høyrup - Vuibert - 2010
• Traité de la résolution des équations numeriques de tous les degrés - J.-L. Lagrange - Duprat - 1798
• Oh, les maths ! - Y. Perelman - Dunod - 1993