Deux inconnues, cela veut dire que nous cherchons maintenant deux nombres. Voici un exemple en algèbre rhétorique :
La somme de deux nombres est égale à 1000. Leur différence est égale à 500. Quels sont ces deux nombres ?
En écriture algébrique, cela signifie que allons avoir besoin d’une deuxième lettre. Comme notre première inconnue s’appelait , la seconde s’appellera . Ainsi, la traduction algébrique de notre équation ci-dessus s’écrira de la façon suivante :
En réalité, ceci se nomme un système d’équations, car comme vous le voyez, nous disposons de deux formules pour trouver nos deux inconnues. Nous reviendrons sur ceci plus en détail à la fin de ce chapitre.
Représentation des solutions
Une solution d’une équation à deux inconnues, c’est la donnée d’une valeur pour et d’une valeur pour . Prenons par exemple l’équation suivante :
Si et , cette égalité est bien vérifiée, en effet, on trouve 9 des deux côtés :
Cependant, cette équation a de nombreuses autres solutions, par exemple et , ou encore et . Comme nous allons le voir dans la suite, le fait d’avoir deux inconnues offre beaucoup plus de liberté et on se retrouve souvent avec des équations ayant beaucoup de solutions
Pour pouvoir mieux s’y repérer il est assez pratique de représenter les solutions dans un repère dans lequel l’inconnue est représenté sur l’axe horizontal et l’inconnue sur l’axe vertical. Par exemple, les trois solutions que nous venons de voir se représentent ainsi :
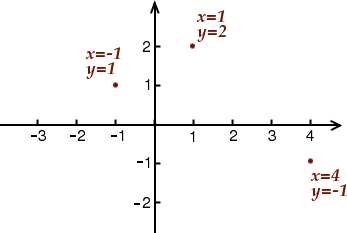
Et on pourrait continuer à chercher d’autres solutions de notre équation pour les placer dans ce repère. On verrait alors apparaître peu à peu la figure suivante :

Grâce à cette représentation des solutions dans un repère, chaque équation donne une figure géométrique. Ce principe est tout bête, mais il est en réalité extrêmement utile car il rend l’étude des équations plus concrète. Une expression algébrique est souvent assez obscure et abstraite, surtout quand on débute, tandis qu’une figure géométrique, c’est visuel et ça rend tout de suite les choses beaucoup plus claires.
Dans notre exemple, on obtient une sorte de cercle aplati qui se nomme une ellipse. Nous verrons un peu plus bas pourquoi.
Notez que cette correspondance marche aussi dans l’autre sens. Quand on fait de la géométrie, il est souvent très utile de chercher les équations des figures que l’on étudie cela permet de mettre toute la puissance de l’algèbre au service des problèmes géométriques.
Méthodes de résolution
Pour résoudre les équations à deux inconnues, nous allons pourvoir réutiliser ce que nous savons sur les équations à une inconnue. Prenons par exemple l’équation suivante :
Autrement dit, on cherche deux nombres dont le produit est égal à 12. Pour trouver une solution on peut procéder de la façon suivante :
- on donne une valeur numérique quelconque à l’une des inconnues, par exemple ;
- notre équation ne contient plus qu’une inconnue, on sait donc la résoudre.
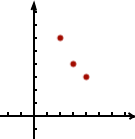
Ceci permet de trouver une solution, et pour en trouver d’autres, il suffit de répéter ce procédé en donnant une autre valeur à . Voici par exemple trois solutions :
- Donnons à la valeur 2, on tombe sur l’équation et on trouve la solution .
- Donnons à la valeur 3, on tombe sur l’équation et on trouve la solution .
- Donnons à la valeur 4, on trouve alors l’équation et on trouve la solution .
Voici comment se placent ces trois solutions dans un repère :
On pourrait continuer longtemps comme ça. Pour chaque valeur de on trouve une valeur de , ce qui permet d’obtenir des solutions à foison. Mais en réfléchissant un peu, on se rend compte qu’il n’est pas vraiment utile de donner des valeurs spécifiques à . On peut se contenter de résoudre l’équation en ne regardant que l’inconnue et en considérant comme un nombre qu’on connait. De cette façon, on trouve tout simplement la solution :
Autrement dit, l’ensemble des solutions de notre équation est composé des couples de nombres de la forme avec qui varie dans .
Vous noterez que varie dans , ce qui signifie que ne peut pas prendre la valeur 0. En effet, dans ce cas, n’est pas défini, car on ne peut pas diviser par 0. Si on remplace par 0 dans l’équation, on trouve et cette équation n’a effectivement pas de solution puisque la multiplication est toujours égale à 0 et ne vaut donc jamais 12.
Au final, la figure géométrique qui correspond à notre équation est la suivante :
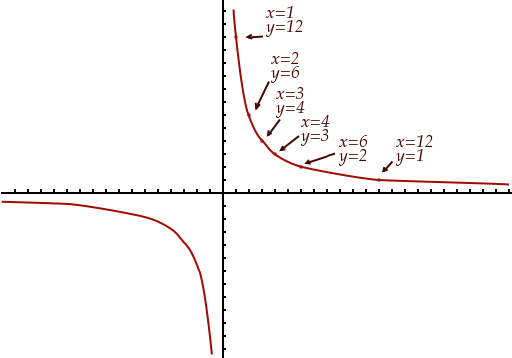
Cette figure se nomme une hyperbole. Vous remarquerez que de cette façon, l’ensemble des points correspond au graphe de la fonction .
La continuité
Il y a une chose qui peut surprendre dans ce que nous venons de voir, c’est de constater à quel point les solutions sont ordonnées. Après tout, on aurait pu s’attendre à ce qu’elles soient toutes dispersées de façon chaotique formant une sorte de nuage de points assez difficile à analyser.
Mais ce n’est pas le cas, on voit que nos solutions s’alignent parfaitement pour former des courbes continues.
Une courbe continue, c’est grosso-modo une figure que l’on peut tracer sur une feuille de papier sans lever le crayon. Dans le cas de l’ellipse que nous avons vu dans la section précédente, nous avons bien une courbe continue. Dans le cas de l’hyperbole, la figure formée par les solutions est composée de deux morceaux continus.
Cette propriété rend les solutions des équations bien plus agréables à visualiser ! Mais pourquoi est-elle vraie ? Toutes les équations donnent-elles toujours des figures continues ?
Cela provient du fait que les transformations que l’on fait subir à nos inconnues sont elles mêmes continues.
Prenons un exemple pour comprendre ce que cela veut dire. Considérons la multiplication qui fournit une solution à l’équation ci-dessus et changeons un tout petit peu ses nombres, remplaçons par exemple 3 par 3,0001 et 4 par 4,002. On trouve alors :
On constate alors que le résultat est également très proche de 12. Et plus les nombres que l’on multiplie sont proches de 3 et de 4, plus leur produit sera proche de 12. C’est cette propriété que l’on appelle la continuité : une opération est continue si quand on effectue cette opération avec des nombres de plus en plus proches, alors les résultats sont eux-même de plus en plus proches.
Ceci explique pourquoi les figures sont continues : si on modifie un tout petit peu , alors ne change lui aussi qu’un tout petit peu. En clair les points se suivent les uns après les autres sans pouvoir faire de grands sauts d’un seul coup. Ils ne peuvent pas être dispersés mais sont obligés de former une ligne continue.
Mais pourtant dans le cas de l’hyperbole, on a une courbe en deux morceaux. Pourquoi n’a-t-on pas un seul morceau continue ?
Parce qu’on utilise une division et que précisément la division n’est pas continue en 0. Regardez les deux divisions suivante :
Vous voyez que les nombres utilisés pour ces deux divisions sont très proches (les dénominateurs sont tous deux très proches de 0) pourtant les deux résultats sont très éloignés. La division n’est pas continue en 0. Il est donc possible à cet endroit d’avoir une rupture de la courbe.
D’une manière générale, si pour résoudre une équation on utilise des opérations qui ne sont pas continues en certains nombres, alors pour chacun de ces nombres il peut y avoir une cassure de la continuité, ce qui donne un morceau supplémentaire dans la figure.
L’addition, la soustraction et la multiplication sont quant à elles parfaitement continues. La division est elle aussi continue partout en dehors de 0. En réalité, la plupart des opérations classiques sont continues. Vous pouvez donc vous rassurer, toutes nos figures géométriques représentant nos solutions sont en général faciles à visualiser.
Équations polynomiales
Les équations par degré
Comme pour les équations à une inconnue, les équations à deux inconnues ne faisant intervenir que les quatre opérations de base et les puissances sont appelées des équations polynomiales. Et de la même façon, elles peuvent être classées selon leur degré.
- S’il n’y a pas de puissance, alors on a une équation du premier degré. Par exemple : .
- S’il y a des carrés, alors on a une équation du second degré. Par exemple : .
- S’il y a des cubes, alors on a une équation du troisième degré. Par exemple .
- Et ainsi de suite pour les degrés suivants.
Il faut cependant faire attention à une subtilité quand les inconnues sont multipliées entre elles. Si par exemple, on a le terme dans notre équation, alors celle-ci est de degré 2, car est une multiplication de deux inconnues comme ou . Pour connaître le degré, il faut donc considérer la multiplication faisant intervenir le plus d’inconnues, même si ce ne sont pas les mêmes. Ainsi, l’équation suivante : est de degré 5 car il y a le terme .
Équations du premier degré
Passons maintenant à l’étude des équations du premier degré qui, comme vous vous en doutez, sont les plus simples à aborder.
Comme pour les équations à une inconnue, il est possible de les réduire par les techniques vues dans la partie précédente (passer tous les termes du même côté, développer, simplifier). Au final, une équation du premier degré à deux inconnues se présente sous la forme classique suivante :
La question qui nous brûle les lèvres est alors la suivante : à quelle figure géométrique cette équation correspond-elle ?
Il est assez facile de faire une conjecture. Il suffit pour cela de prendre une équation du premier degré et de placer plusieurs solutions pour se faire une idée. Si par exemple on considère l’équation alors en donnant à les valeurs successives 0, 1, 2, 3, 4 et 5 on trouve les points suivants :
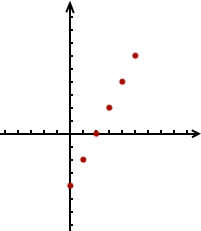
Alors ? Quel est votre pronostique ? Il n’est pas très difficile en voyant ces points de deviner que la figure va être une ligne droite. Et si vous doutez encore, vous pouvez essayer de placer d’autres points en choisissant d’autres valeurs de , vous constaterez que vos nouveaux points seront toujours alignés avec les autres.
Au final, la figure semble être celle-ci :
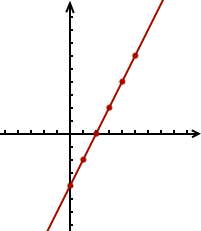
Mais comment expliquer ce phénomène ? Est-ce un cas particulier ou bien toutes les équations du premier degré sans exception se représentent-elles par des droites ?
Pour répondre à cette question, commençons par trouver une caractérisation des droites à partir des coordonnées de leurs points. Regardons la droite suivante sur laquelle nous avons placé un point :
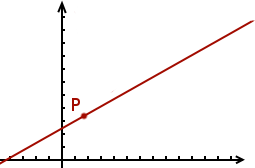
À partir de ce point, plaçons deux autres points et sur la droite et notons et les deux points suivants :
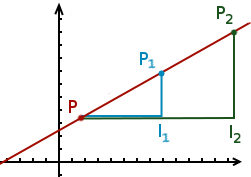
Ainsi on a :
- est le décalage horizontal entre et ;
- est le décalage vertical entre et ;
- est le décalage horizontal entre et ;
- est le décalage vertical entre et .
Nous nous trouvons alors dans la configuration du théorème de Thalès ! Les triangles et sont semblables et on a donc l’égalité suivante :
Cette égalité peut se formuler de la façon suivante : sur une droite, le rapport entre le décalage vertical de deux points et leur décalage horizontal est constant. En d’autres termes, les décalages horizontaux et verticaux sont proportionnels !
Cette propriété caractérise les droites. Ainsi il suffit de montrer que les points qui représentent les solution de nos équations du premier degré vérifient cette propriété pour montrer qu’il correspondent bien à une droite.
Considérons donc deux solutions de notre équations et notons les et . On a donc :
$$ ax_1+by_1+c=0 \text{et} ax_2+by_2+c=0.$Le décalage horizontal entre ces deux points est égal à $x_1−x_2 et leur décalage vertical à . Pour pouvoir comparer les deux, faisons la différence de nos deux équations ci-dessus :
On constate alors que le nombre s’élimine et que l’on peut factoriser cette égalité de la façon suivante :
Il ne reste plus qu’à passer la différence à droite de l’égalité et à diviser par pour obtenir :
Et c’est gagné ! Cette formule affirme précisément que est proportionnel à et le coefficient de proportionnalité est égal à .
Ce coefficient s’appelle le coefficient directeur de la droite et peut s’interpréter comme la pente de celle-ci. S’il est égal à 0 la droite est horizontale, s’il est positif la droite monte et s’il est négatif la droite descend. Notez que si ce coefficient n’est pas défini, ce qui correspond au cas où la droite est verticale : sa pente est infinie !
L’ensemble des solutions d’une équation du premier degré à deux inconnues est donc toujours une droite ! C’est un joli résultat, vous ne trouvez pas ?
Équations du second degré
Après le premier degré vient le second. Une équation du second degré à deux inconnues s’écrit de la façon suivante :
Ça fait peur, hein ? Rassurez-vous, nous n’allons pas entrer dans le détail de ces équations. Sachez simplement que les figures géométriques que l’on obtient s’appellent les coniques. Nous en avons déjà vu deux exemples au début de ce chapitre : l’ellipse et l’hyperbole.
Le nom des coniques vient du fait que ces figures correspondent à l’intersection entre un plan et un cône. Il existe trois types de coniques : les ellipses, les paraboles et les hyperboles. Les ellipses sont des figures finies, tandis que les paraboles et hyperboles ont toutes deux des branches qui partent à l’infini.
| Ellipse | Parabole | Hyperbole |
|---|---|---|
 |
 |
 |
 |
 |
 |
L’étude de ces équations du second degré est assez longue et nécessite de distinguer de nombreux cas de figure différents, mais dans le fond, les méthodes utilisées sont semblables à celles utilisées pour la résolution des équations du second degré à une seule inconnue. Si vous voulez en savoir plus n’hésitez pas à consulter un cours sur le sujet.
Système d'équations
Un système d’équation, c’est la donnée de plusieurs équations que l’on doit résoudre simultanément. Au début du chapitre, nous avons vu l’exemple suivant :
Ce qui signifie que l’on cherche deux nombres dont la somme vaut 1000 et la différence 500. Il ne suffit pas que l’une des deux soit vérifiée, on veut deux nombres qui satisfont les deux à la fois.
Vous aurez constaté de vous-même que l’on note un système en regroupant ses équations à l’aide d’une accolade à gauche.
Nous avons vu que les solutions d’une équation à deux inconnues sont représentées par une courbe, ce qui signifie que la plupart du temps il y a une infinité de solutions. Le fait de rajouter une deuxième équation donne une seconde contrainte qui permet de limiter les solutions.
Nous verrons dans le chapitre suivant que la plupart du temps, quand on étudie des équations avec plusieurs inconnues, il faut considérer un système comportant autant d’équations que d’inconnues pour n’avoir qu’un nombre fini de solutions. Ainsi, quand on étudie des problèmes à deux inconnues, ils est fréquent d’avoir deux équations.
Équations du premier degré
Nous avons vu qu’une équation du premier degré se représente par une droite. Ainsi, si on dispose d’un système de deux équations de degré 1, cela nous donne deux droites et la solution recherchée se trouve à l’intersection.
Regardons ce que cela donne pour l’exemple ci-dessus :
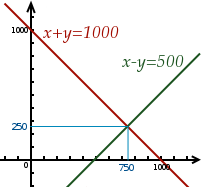
Les nombres qui vérifient se trouvent sur la droite rouge et ceux qui vérifient , sont sur la droite verte. Le seul point qui se trouve à la fois sur la rouge et la verte est celui de coordonnées . Notre système a donc une unique solution :
Deux droites quelconques ont presque toujours un et un seul point d’intersection, sauf si elles sont parallèles. Dans ce cas, le système n’a pas de solution.
En fait, le cas où les droites sont parallèles se présente quand les deux équations sont dépendantes l’une de l’autre par exemple dans le cas suivant :
Il est évident que ce système n’a pas de solution car ne peut pas être égal à la fois à 7 et à 2.
Pour que les droites ne soient pas parallèles, il faut que leurs coefficients directeurs ne soient pas les mêmes, autrement dit que le rapport ne soit pas le même dans les deux équations, sinon on tombe sur un cas impossible comme ci-dessus.
Méthode de résolution
Il existe plusieurs façons de résoudre un système d’équation, mais la plus générale qui marche quasiment à tous les coups est la suivante :
- On résout la première équation avec l’inconnue en considérant comme un nombre, comme nous l’avons déjà vu au début du chapitre.
- Une fois qu’on a trouvé la valeur de en fonction de , on prend la deuxième équation et on remplace toutes les occurrences de par l’expression que l’on vient de trouver.
- On tombe alors sur une équation à une seule inconnue : . Il n’y a plus qu’à résoudre celle-ci pour trouver , puis à déduire à partir de la valeur de .
Ça a l’air compliqué comme ça, mais vous allez voir qu’avec un exemple tout va s’éclairer. Reprenons notre système préféré :
On commence à résoudre la première équation pour trouver . C’est facile, il suffit de passer le de l’autre côté :
On remplace tous les de la deuxième équation par . Ici il n’y en a qu’un :
Nous avons maintenant une simple équation du premier degré à une inconnue que nous savons résoudre :
Et le se déduit immédiatement :
Heureusement, nous trouvons la même solution par cette méthode qu’avec l’intersection des droites sur le graphique : et . Ouf !
Si vous avez compris le principe, il ne vous reste plus qu’une chose à faire : résoudre des équations, résoudre des équations, encore résoudre des équations, toujours résoudre des équations ! Apprendre les méthodes est une chose utile pour débuter et comprendre ce qu’il faut faire, mais seule la pratique vous permettra de vraiment pouvoir prétendre maîtriser le sujet et ses nombreuses subtilités.