Si une équation, au lieu de donner une égalité, nous donne une inégalité, alors on appelle cela une inéquation. En voici un exemple :
Trouver un nombre dont le carré est plus petit que le triple.
Ce qui en langage algébrique se traduit de la façon suivante :
À quelques adaptations près, la plupart des techniques que nous avons vues pour les équations fonctionnent également pour les inéquations. Nous allons voir dans cette annexe comment les aborder.
Plus grand ou plus petit
Les quatre inégalités
Il existe quatre types d’inégalités, classées selon deux critères :
- Infériorité ou supériorité : indique si le nombre qui est à gauche de l’inégalité est inférieur ou supérieur à celui de droite.
- Large ou stricte : indique si le cas d’égalité est compté ou pas. Au sens large, un nombre est considéré comme inférieur (ou supérieur) à lui-même, au sens strict, ce n’est pas le cas. Voici un tableau qui résume ces quatre possibilités :
Infériorité | Supériorité | |
|---|---|---|
Stricte | ||
Large | ou | ou |
La nuance entre inégalité large ou stricte fait qu’une phrase telle que « est inférieur à » est ambiguë. Pour éviter toute confusion, il faut mieux préciser à chaque fois : « est inférieur ou égal à » ou « est strictement inférieur à ».
Trouver les zones
Contrairement aux équations dont les solutions sont souvent quelques nombres isolés, les inéquations ont la plupart du temps des intervalles entiers de solutions. Prenons par exemple l’équation suivante :
Il s’agit d’une équation polynomiale sous sa forme factorisée, il est donc facile d’identifier ses solutions : 0, 2 et 5. Celles-ci peuvent se représenter comme ceci sur la droite réelle :

Ces trois solutions délimitent quatre zones sur lesquelles l’expression est positive ou négative. Prenons par exemple, l’intervalle compris entre 0 et 2, si on teste par exemple avec le nombre 1, on trouve :
Ce test permet de dire qu’entre 0 et 2, l’expression est positive. En testant de même pour les trois autres zones, on constate que le résultat est également positif pour l’intervalle et qu’il est négatif dans les deux autres.
Ainsi, si on considère l’inéquation , alors l’ensemble des solutions est la réunion des deux intervalles :
Voici les quatre différentes configurations selon l’inégalité choisie :
| Inéquation | Représentation des solutions | Solutions |
|---|---|---|
 |
||
 |
||
 |
Petit rappel sur les intervalles. Un intervalle est fermé si il contient ses deux extrémités, il se note alors avec des crochets tournés vers l’intérieur, comme . Au contraire, on dit que l’intervalle est ouvert si les deux extrémités sont exclues et on tourne alors les crochets vers l’extérieur. En bref, si on a une inéquation large, les intervalles de solutions seront fermés et si l’inéquation est stricte ils seront ouverts.
Avec la pratique, vous verrez que la plupart du temps les expressions changent de signe en passant par 0. Ainsi, les zones positives et négatives alternent à chaque solution de l’équation. Mais attention ce n’est pas systématique : le contre-exemple le plus simple est qui s’annule pour mais sans changer de signe puisqu’un carré est toujours positif.
Méthode de résolution
La plupart des techniques de manipulation d’équations marchent de la même façon pour les inéquations. Il y a cependant quelques petites subtilités que nous allons voir maintenant.
Dans cette section nous n’allons traiter que des exemples de supériorité stricte, mais tout ce que nous allons dire marche également dans les trois autres cas.
Tous à gauche !
Si on a une inéquation, il est possible d’ajouter ou de soustraire le même terme à gauche et à droite sans en changer les solutions. En schéma cela donne ceci :
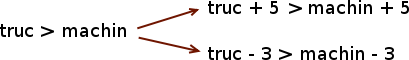
Cette propriété est vraiment fondamentale car c’est elle qui nous permet de passer tous les termes du même côté pour simplifier nos équations. Ainsi, comme pour les équations, toutes les inéquations peuvent se réécrire sous la forme :
Multiplions
Lorsque l’on a besoin de multiplier les termes d’une inéquation, en revanche, il y a un piège. Si on multiplie des deux côtés par un nombre positif, pas de problème, cela marche de la même façon, en revanche, si on multiplie par un nombre négatif, alors le sens de l’inégalité est changé.
En bref, on a la règle suivante :
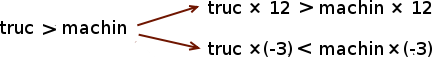
Cela marche évidemment de la même manière avec les divisions puisqu’une division n’est jamais qu’un cas particulier de multiplication. Diviser par un nombre, c’est multiplier par son inverse.
Prenez bien le temps d’y réfléchir, car dans le fond cette règle est tout à fait logique même si elle est surprenante quand on la voit pour la première fois. Quand on multiplie par un nombre négatif on renverse la droite des nombres : les positifs deviennent négatifs, les négatifs positifs et du coup les plus grands deviennent plus petits et les plus petits plus grands.
Ainsi, si par exemple votre inéquation est , alors en divisant par -2 des deux côtés on trouve ! L’ensemble des solutions est donc .
Méfiez-vous réellement de cette règle, c’est sans nul doute l’erreur numéro 1 que font les débutants.
Tableaux de signes
Lorsque notre inéquation se présente sous une forme factorisée, c’est-à-dire qu’elle est le produit de plusieurs termes plus simples, alors il est possible d’étudier le signe de chacun de ces termes séparément avant de tout regrouper grâce à la règle de multiplication des signes.
Considérons par exemple l’inéquation suivante :
Nous avons la multiplication de trois termes :
- est négatif si et positif si ;
- est toujours positif ;
- est négatif si et positif si .
Finalement, nous avons deux valeurs frontière où un changement de signe est possible : 0 et 2. Nous pouvons récapituler ce que nous venons de dire dans le tableau suivant :
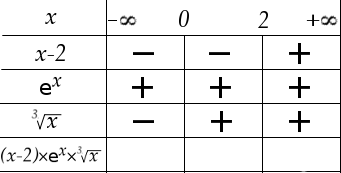
Il ne reste plus qu’à remplir la dernière ligne. Pour cela il faut se rappeler de la règle de multiplication des signes : si on multiplie un nombre par un nombre positif, cela ne change pas son signe tandis que si on le multiplie par un nombre négatif, son signe est inversé.
Ainsi, dans chaque colonne, il suffit de compter le nombre de signes négatifs. S’il y en a un nombre pair, alors le produit est positif, et s’il y en a un nombre impair alors le produit est négatif. Le tableau se complète donc de la façon suivante :
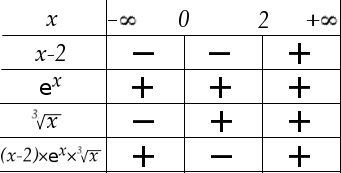
L’ensemble des solutions de notre inéquation est donc l’intervalle .
À vous de jouer
Vous avez maintenant toutes les clefs en main pour pouvoir résoudre l’équation donnée en préambule de cette annexe : trouver les nombres ayant un carré plus petit que leur triple.
Essayez de trouver la réponse par vous-même avant de regarder la solution, et si vous avez un doute n’hésitez pas à retourner lire ce que nous avons vu plus haut.
Nous cherchons donc à résoudre l’équation suivante :
Comme nous l’avons vu, la première chose à faire est de tout passer du même côté :
Nous pouvons maintenant factoriser :
Et il ne reste plus qu’à dresser notre tableau de signe :
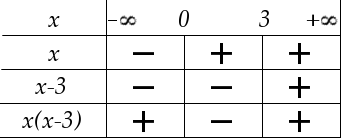
L’ensemble des solutions de notre inéquation se résume à l’intervalle . Bravo si vous aviez trouvé !