Les équations du premier degré sont les plus simples que l’on puisse trouver. Ce sont celles dans lesquelles les seules transformations que subit l’inconnue sont les quatre opérations de base : addition, soustraction, multiplication et division. Voici un exemple :
Cependant, nous avons déjà vu dans le deuxième chapitre de ce cours qu’avec quelques manipulations de base, toutes ces équations peuvent se réduire à la forme :
Par exemple, est une équation du premier degré. C’est de cette forme de base que nous allons partir dans ce chapitre.
La résolution
Tout de suite une bonne nouvelle : cette section va être courte. En effet, nous savons déjà tout ce qu’il faut savoir pour résoudre les équations du premier degré : l’inconnue n’apparaît qu’une seule fois dans la forme , il suffit donc de deux petites transformations pour aboutir à la solution :
Le schéma de l’équation est le suivant.

Les deux opérations étant réversibles, le schéma de résolution s’obtient facilement en inversant le chemin :

Nous avons donc la solution de notre équation :
Nous venons de résoudre l’équation sans problème grâce à nos petits schémas, mais remarquez que l’on serait arrivé au même résultat en utilisant uniquement le langage algébrique :
La première étape consiste à faire passer le de l’autre côté en le soustrayant et la seconde fait passer le de l’autre côté en divisant. Ceci permet d’obtenir le tout seul.
L’utilisation du symbole d’équivalence, , dans la résolution ci-dessus signifie que les équations considérées ont les mêmes solutions. Le fait que la flèche soit à double sens est très important, et vient du fait que l’on utilise des opérations réversibles, comme nous l’avons vu dans la première partie du cours. Si on utilisait des opérations non réversibles comme le carré, alors la flèche n’irait que dans un sens (), ce qui signifie que l’on ne peut pas revenir en arrière et que de nouvelles solutions peuvent être apparues.
Rassurez-vous, nous n’allons pas abandonner tout de suite nos schémas de résolution, mais nous allons commencer une transition en douceur et il va falloir que vous vous habituiez peu à peu à résoudre les équations grâce au langage algébrique. Ça peut sembler un peu abstrait au départ, mais c’est tellement plus pratique une fois qu’on le maîtrise.
Quelques énigmes
Après la théorie, la pratique. Dans cette section, je vous propose quelques énigmes qui se résolvent grâce à des équations du premier degré. Essayez de chercher les réponses par vous-même avant de regarder les solutions !
La bosse des équations
Au zoo, dans l’enclos des chameaux et des dromadaires on peut compter 12 têtes et 17 bosses. Combien y a-t-il de chaque animal ?
Pour pouvoir répondre, il est bon de savoir qu’un chameau a deux bosses tandis qu’un dromadaire n’en a qu’une.

La première chose à faire quand on se retrouve face à une énigme comme celle-ci, c’est la traduire dans notre merveilleux langage algébrique. Et pour cela, il faut commencer par décider ce que représente l’inconnue. Ici, nous cherchons deux choses : le nombre de chameaux et le nombre de dromadaires, l’inconnue peut donc être l’un au l’autre de ces nombres.
Décidons par exemple de noter le nombre de chameaux. Comme il y a 12 têtes cela signifie qu’il y a 12 animaux, il y a donc dromadaires. À partir de là, nous pouvons compter les bosses :
- il y a chameaux à deux bosses, ce qui fait bosses ;
- il y a dromadaires à une bosse, ce qui fait bosses.
Au total, il y a donc bosses. Or on sait que ce nombre vaut 17, ce qui donne l’équation suivante :
Et voilà ! Il n’y a maintenant plus qu’à appliquer ce que nous avons appris à faire pour résoudre cette équation.
Il y a donc 5 chameaux et 7 dromadaires.
Notez que l’exemple est si simple que nous n’avons même pas pris la peine de passer par la forme standard . Si on avait voulu le faire, on aurait obtenu et donc et , ce qui donne bien .
L’épitaphe de Diophante
L’énigme que nous allons voir maintenant est sans doute la plus célèbre de toutes les équations du premier degré de l’histoire des mathématiques. Il s’agit de l’épitaphe (texte gravé sur la tombe) du mathématicien Diophante d’Alexandrie qui a vécu au IIIe siècle. Voici une traduction de ce que l’on pouvait lire sur cette tombe :
Passant, sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s’écoula,
Puis s’étant marié, sa femme lui donna
Cinq ans après un fils qui, du destin sévère
Reçut de jours hélas ! deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, si tu sais compter, à quel âge il mourut.
Alors et vous ? Êtes-vous capable de dire à quel âge Diophante est mort ?
Clairement l’inconnue de ce problème est l’âge de Diophante, notons-le donc . L’épitaphe découpe la vie de Diophante en plusieurs tranches :
- son enfance qui dure un sixième de sa vie soit ;
- son adolescence qui dure un douzième de sa vie soit ;
- entre son adolescence et son mariage il s’écoule un septième de sa vie soit ;
- entre son mariage et la naissance de son fils il s’écoule 5 ans ;
- son fils a vécu deux fois moins longtemps que lui soit ;
- après la mort de son fils il s’écoule encore 4 ans.
La durée de sa vie est égale à la somme de tous ces termes, on obtient donc l’équation suivante :
Il n’y a maintenant plus qu’à résoudre :
Nous avons donc et . Il suffit maintenant simplement soit de passer ces deux termes de l’autre côté, soit d’appliquer directement la formule que nous avons vue dans la section précédente si vous vous en souvenez :
Diophante est donc mort à l’âge de 84 ans, un bel âge pour l’époque !
Quel âge ?
Un jeune homme de 21 ans demande son âge à un autre. Ce dernier lui répond : « j’ai deux fois l’âge que vous aviez quand j’avais l’âge que vous avez ». Mais quel âge a-t-il ?
Le plus dur dans cette énigme, ce n’est pas de résoudre l’équation, c’est de réussir d’abord à trouver l’équation sans s’embrouiller à partir de l’énoncé. Faites chauffer vos neurones et réfléchissez tranquillement vous pouvez y arriver !
Commençons par dire que notre inconnue désigne cette fois l’âge de l’homme. Ainsi cet homme a années de plus que le jeune homme de 21 ans. L’expression « quand j’avais l’âge que vous avez » peut donc être remplacée par « il y a ans ». L’homme a donc dit :
« J’ai deux fois l’âge que vous aviez il y a ans »
Or le jeune homme a 21, donc, il y a ans, il avait ans. L’homme prétend donc avoir deux fois cet âge, ce qui revient à l’équation suivante :
Le plus dur est fait ! Il n’y a plus qu’à résoudre :
L’homme a donc vingt-huit ans !
Représentation graphique
Lorsque l’on a une équation dont on a passé tous les termes à gauche, il est possible de considérer la fonction associée. Pour les équations du premier degré, ces fonctions sont celles de la forme :
Ces fonctions se nomment des fonctions affines.
Pour en savoir plus sur les fonctions, vous pouvez vous reporter au cours Introduction aux fonctions.
Quand on étudie une équation, on ne s’intéresse finalement qu’aux valeurs de pour lesquelles est égal à 0. En étudiant la fonction en général, on regarde également ce que donne cette expression pour d’autres valeurs de . À première vue cela peut sembler superflu, mais en réalité cela permet de prendre du recul et donc de mieux comprendre le fonctionnement de l’équation.
Quand on a une fonction réelle, on peut la représenter dans un repère composé de deux axes : celui des abscisses (horizontal) et celui des ordonnées (vertical) :
Prenons par exemple la fonction affine , alors on place les points de la façon suivante : pour chaque , on met dans le repère un point ayant pour abscisse et pour ordonnée . Voici trois exemples :
- si , alors ;
- si , alors ;
- si , alors .
Cela donne les trois points suivants :
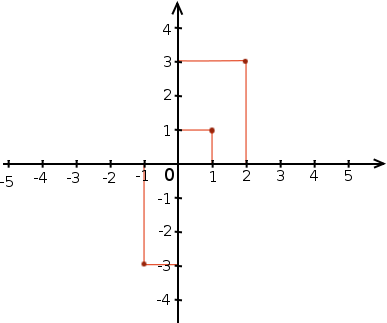
Et si on trace tous les points en faisant varier , on obtient une droite :
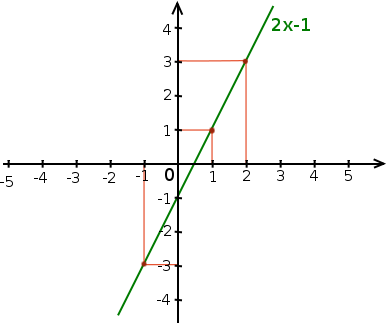
Le fait d’obtenir une droite est tout à fait normal, c’est justement la particularité des fonctions affines. Toutes les fonctions affines se représentent par une droite et les paramètres et jouent de la façon suivante :
- Le nombre s’appelle le coefficient directeur et représente la pente de la droite. Si est positif, la droite monte de gauche à droite et plus est grand, plus elle monte vite. Si au contraire est négatif, la droite descend.
- Le nombre , s’appelle l’ordonnée à l’origine, c’est la hauteur à laquelle la droite coupe l’axe des ordonnées.
Voici quelques exemples de droites obtenues de cette façon :
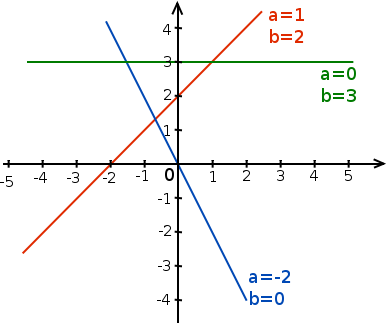
Je ne vous en dis pas plus sur les représentations des fonctions car ce n’est pas l’objet de ce cours. Si vous voulez comprendre plus en détail pourquoi on obtient des droites et ce qui se passe quand a et b varient, vous pouvez vous reporter à un cours sur les fonctions.
Les solutions de l’équation correspondent alors aux points où la fonction vaut 0, c’est-à-dire aux intersections avec l’axe des abscisses.
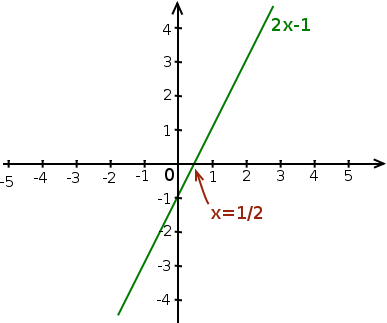
Vu que les fonctions affines sont des droites, elles coupent l’axe des abscisses en un seul point qui correspond à la solution que nous avions trouvée. Voici sa représentation pour l’équation pour laquelle on trouve bien .
Il existe une exception pour laquelle, la droite ne coupe pas l’axe des abscisses : si elle est parallèle à celui-ci. Cela signifie que , donc que l’inconnue disparaît dans notre équation qui devient simplement . Une équation sans inconnue ! Voilà qui est très étrange. Il y a alors deux cas :
- si n’est pas égal à 0, l’égalité est toujours fausse et donc l’équation n’a aucune solution ;
- si est égal à 0, l’équation devient juste 0=0 qui est toujours vrai, donc tous les nombres sont solutions.
Dans ce cas, notre droite est confondue avec l’axe des abscisses.