Dans les trois derniers chapitres, nous avons étudié les équations polynomiales, c’est-à-dire celles faisant intervenir les quatre opérations de base et les puissances. Mais il existe encore de nombreuses opérations en mathématiques que l’on peut mettre dans nos équations :
- les racines carrée, racines cubiques, et racines d’ordre supérieur ;
- les logarithmes et les exponentielles ;
- les fonctions trigonométriques : sinus, cosinus, tangentes…
J’en passe et c’est sans compter les multiples combinaisons que l’on peut faire en utilisant toutes ces fonctions ! Lorsque l’on se trouve face à une telle transformation, le premier principe que l’on cherche à appliquer est toujours celui que nous avons vu dans la première partie de ce cours : remonter vers l’inconnue en appliquant les transformations inverses. C’est ce que nous allons apprendre à faire dans ce chapitre.
Ce cours n’est pas un cours sur les fonctions et n’a pas pour but d’expliquer comment fonctionnent les opérations qui suivent. Si vous n’en connaissez pas certaines, reportez-vous à un cours sur le sujet ou passez votre chemin le temps de les avoir apprises.
Racines
Racine carrée
Commençons par la racine carrée. Dans les nombres réels, la fonction racine carrée n’est définie que sur les nombres positifs et donne toujours un nombre positif. Son graphe est le suivant :

La fonction racine carrée est l’inverse du carré, ainsi, pour la remonter, il suffit de prendre le carré. Si par exemple on a l’équation suivante :
sa seule solution est . Si en revanche la racine donne un résultat négatif, comme dans l’équation suivante :
alors l’équation n’a pas de solution.
Attention, à ne pas élever l’équation précédente au carré : c’est un piège. En effet, comme nous l’avons vu dans la première partie du cours, le fait d’élever une équation au carré peut faire apparaître de fausses solutions et c’est se qui se passe ici : on obtient , mais 25 n’est pas réellement solution puisque .
Racine cubique
Pour la racine cubique c’est plus simple car elle est définie pour tous les nombres, mêmes négatifs. Son graphe est le suivant.
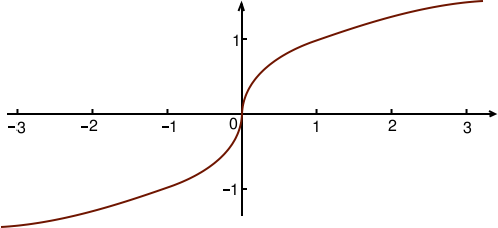
Pour remonter une racine cubique, il suffit de prendre le cube. Par exemple, l’équation suivante :
possède une unique solution : .
Racines d’ordre supérieur
Pour les racines d’ordre supérieur, la règle est la suivante :
- si la racine est paire, alors, elle se comporte comme la racine carrée et n’est définie que pour les nombres positifs ;
- si la racine est impaire, alors, elle se comporte comme la racine cubique et est définie pour tous les nombres réels.
Voici trois exemples de résolution :
Équation | Résolution |
| |
| 12 est pair et -3 est négatif : pas de solution. |
|
Exponentielles et logarithmes
Exponentielles
On parle d’exponentielle lorsque l’on a une puissance, mais que l’inconnue se trouve en exposant comme dans l’équation suivante :
L’opération qui permet de remonter l’exponentielle est le logarithme de même base. Ainsi, la solution de l’équation ci-dessus est .
Dans cet exemple, on a une exponentielle de base 3, mais la plupart du temps, en mathématiques, on rencontre l’exponentielle de base qui possède des propriétés qui la rendent agréable à manier. Le logarithme de base e se nomme le logarithme népérien et se note .
Les graphes des fonctions exponentielles ressemblent à ceci :
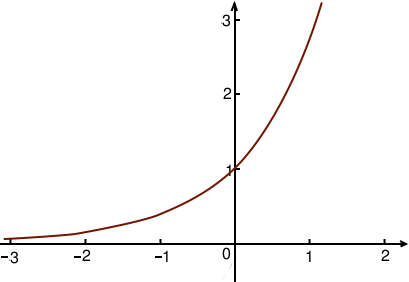
Comme pour la racine carrée, vous voyez que cette fonction ne prend pas de valeurs négatives. Ainsi ces équations n’ont pas de solution si elles demandent à une exponentielle d’être négative. Si au contraire l’exponentielle est bien positive, alors elle s’inverse grâce au logarithme de même base.
Voici deux exemples d’équations exponentielles :
Équation | Résolution |
-1 est négatif : pas de solutions. |
Notez que l’exponentielle est toujours donnée dans une base positive. Les exponentielles à base négative comme par exemple ne sont pas définies en général et demandent l’intervention des nombres complexes quand cela est possible.
Logarithmes
Intéressons nous maintenant aux équations faisant intervenir un logarithme, comme par exemple :
Les fonctions logarithme ont un graphe de la forme suivante :
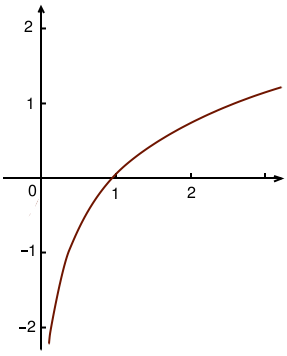
Cette fonction passe par toutes les valeurs, positives et négatives, elles sont donc toujours résolubles. Pour remonter un logarithme, on utilise l’exponentielle de même base, voici un exemple :
Équation | Résolution |
Fonctions trigonométriques
Passons maintenant aux fonctions trigonométriques, il y en a principalement trois : le cosinus, le sinus et la tangente.
Attention, la définition des fonctions trigonométriques dépend de l’unité d’angle choisie. La mesure la plus classique est celle en radians pour laquelle, un tour complet mesure (soit environ 6,28), un demi-tour mesure et un angle droit mesure . C’est cette convention que nous utiliserons.
Le cosinus
Le graphe du cosinus ressemble à ceci :
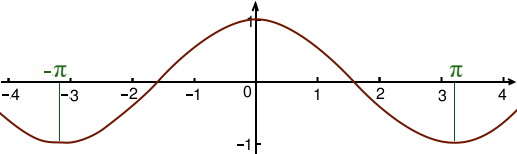
En fait, le cosinus est -périodique ce qui signifie que si on fait un zoom arrière, le motif se répète tous les , il oscille entre -1 et 1 :

Tout d’abord remarquons que comme cette fonction ne sort pas d’un intervalle allant de -1 à 1, alors l’équation
ne possède pas de solution si ou si .
Si en revanche , nous nous retrouvons dans une situation que nous n’avons encore jamais connue car avec cette périodicité, les équations faisant intervenir un cosinus ont une infinité de solutions. Regardons par exemple l’équation suivante :
On peut voir sur le graphe que la fonction cosinus passe une infinité de fois par la valeur 1/2, il y a donc bien une infinité de solutions.
Si vous connaissez vos tables trigonométriques, vous savez que l’un des angles dons le cosinus vaut 1/2 est celui de , ainsi l’une des solutions est . À partir de là, vu que la fonction est -périodique, tous les nombres suivants sont solutions :
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Bon je ne vais pas les écrire tous car vous avez compris qu’il y en a une infinité. Tous les nombres de la forme avec un nombre entier (positif ou négatif) sont solutions.
Mais même quand on a donné ceux-là on ne les a pas encore tous ! En effet, vu que la fonction cosinus est paire (c’est-à-dire que son graphe est symétrique par rapport à l’axe vertical) alors à chaque fois que l’on a une solution, son opposé est également solution. Il faut donc ajouter toutes les solutions suivantes :
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
Au final, les solutions de l’équation sont les nombres de la forme avec .
Mais comment fait-on si le cosinus de l’inconnue n’est pas égal à 1/2, mais à un autre nombre ?
On utilise la fonction arc cosinus ! Si est un nombre entre -1 et 1, alors est le nombre dont le cosinus vaut qui se trouve entre et . Pour reprendre l’exemple ci-dessus, on a
Ainsi, par un raisonnement identique à celui que nous venons de faire pour 1/2, si on considère l’équation
avec compris entre -1 et 1, alors une de ses solutions est et on peut en déduire que toutes ses solutions sont les nombres de la forme avec .
Notez que c’est le même principe que pour le carré qui donne deux solutions : dans ce cas, le symbole désigne la racine positive et la seconde solution se trouve en prenant l’opposé. Dans les deux cas, on a un symbole spécifique qui donne l’une des solutions et à partir de cette solution, on reconstruit toutes les autres.
En résumé, voici deux exemples d’équations avec un cosinus :
Équation | Résolution |
7 est plus grand que 1 : pas de solution. |
Le sinus
Le fonctionnement est identique pour le sinus. Son graphe est le même que pour le cosinus, mais décalé de vers la droite.
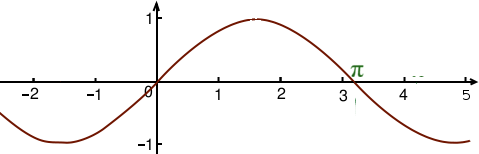
La fonction qui permet de retrouver le nombre entre et dont le sinus est égal à un nombre donné est l'arc sinus. Ainsi, si on a l’équation suivante :
avec compris entre -1 et 1, alors est l’une des solutions. Comme pour le cosinus on trouve d’autres solutions en ajoutant des multiples de à ce nombre.
D’autre part, comme le graphe est symétrique par rapport à un axe vertical d’abscisse , cela signifie que est aussi une solution. Au finale, l’ensemble des solutions de l’équation est composé des nombres de type ou avec .
La tangente
Pour la tangente, on a cette fois un graphe -périodique :

Vous remarquez que contrairement au cosinus et au sinus, la tangente passe par toutes les valeurs. Ainsi, l’équation
a toujours des solutions. Pour trouver la solution qui se trouve entre et , on utilise l'arc tangente. Ainsi, les solutions de l’équation sont les nombres de la forme avec un nombre entier.
Vous remarquez qu’on ajoute bien et non pas puisque la tangente est -périodique.
Un exemple
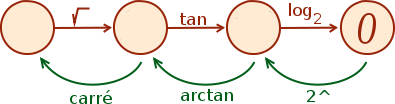
Pour récapituler tout ce que nous venons de dire, j’ai envie de vous lancer un petit défi. Sauriez-vous résoudre l’équation suivante :
Si l’on reprend nos bons vieux schémas d’équations, on a donc ceci :

Essayez de trouver la (ou les) solution(s) par vous-même avant de regarder les explications qui suivent.
Solution
Comme nous l’avons déjà fait avec les opérations élémentaires, il s’agit de remonter vers l’inconnue en suivant le parcours vert de droite à gauche :
La première étape est facile, nous savons que pour remonter un logarithme, il faut utiliser une exponentielle de même base, ainsi on trouve .
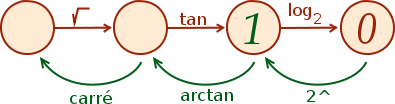
Pour remonter la tangente, on utilise l’arc tangente. Si vous regardez dans une table trigonométrique vous pourrez voir que . Mais il ne faut pas oublier que comme la tangente est -périodique, on a une infinité de solutions en ajoutant les multiples de à .
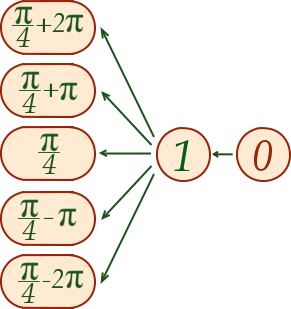
Seules cinq solutions sont représentées sur le schéma, mais il ne faut pas oublier qu’il y en a une infinité. Il faut imaginer que le schéma se prolonge infiniment vers le haut et vers le bas avec tous les nombres de la forme .
Il ne reste plus qu’à remonter la racine. Rappelez-vous qu’il n’y a de solution que quand le résultat de la racine est positif. Ainsi, la moitié des nombres que nous avaient donnés la tangente sont sans issue. Il nous reste cependant tous ceux de la forme avec positif qu’il suffit de mettre au carré.
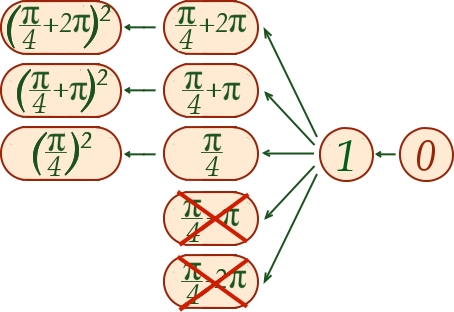
Et voilà le travail ! Les solutions de notre équation sont les nombres de la forme avec .
Résolution sérieuse
Nous venons de résoudre notre équation grâce à nos schémas, mais bien sûr, le même raisonnement peut se faire uniquement en écriture algébrique :
Encore une fois, si cette écriture algébrique vous parait rébarbative, faîtes tout de même l’effort de la lire en détail en comparant à la résolution par les schémas. Cette écriture est réellement beaucoup plus puissante et agréable à utiliser une fois qu’on la maîtrise.