|
|
mercredi 20 février 2019 à 12h38
|
Non, je lui ai directement envoyé la séquence par mail. Il y en a aussi une autre très proche de celle-ci : $PGCD(n!^2+1,\sigma(n)!)$ qui semble avoir un comportement similaire. Le contre-exemple pou…
|
|
|
mercredi 20 février 2019 à 11h18
|
Bonjour,
J'ai contacté Eric Rowland qui m'a trouvé un contre-exemple pour n=7880, on trouve 380927609 qui est composé.
Néanmoins il m'a dit que la séquence était intéressante et pouvait être po…
|
|
|
dimanche 17 février 2019 à 18h45
|
Bonjour,
En partant de la formule d'Eric Rowland : https://arxiv.org/pdf/0710.3217.pdf j'ai pu constater que la formule suivante donnait également soit 1 soit un nombre premier.
La formule en q…
|
|
|
lundi 14 janvier 2019 à 18h45
|
Bonjour,
Effectivement j'ai oublié, c'est la somme des diviseurs de l'entier n (n compris).
|
|
|
lundi 14 janvier 2019 à 16h36
|
Bonjour,
J'aimerais comprendre ce rapport $\frac{\sigma(n*\sigma(n))}{m}, m = \sigma(n)$
Pourquoi parfois le résultat vaut bien $\sigma(m)$ et parfois non ?
Exemple avec n=50 : $\frac{\sigma…
|
|
|
vendredi 30 novembre 2018 à 09h22
|
Bonjour à tous,
Je reviens avec de nouvelles informations.
En fait il s'agit d'une reformulation de la conjecture de l'infinité des nombres de Mersenne premiers (conjecture non résolue, même si l…
|
|
|
lundi 26 novembre 2018 à 09h43
|
Merci pour la réponse.
Après je ne sais pas comment expliquer pourquoi on trouve souvent les mêmes entiers. J'ai pu aller plus loin avec le code python (et en réduisant le temps de recherche en re…
|
|
|
lundi 26 novembre 2018 à 02h55
|
En effet il y a une limite.
Je viens d'essayer ce test en ligne : https://www.alpertron.com.ar/ECM.HTM
Quand j'entre le nombre et que je mets factor il semble ne rien trouver (j'ai laissé tourner…
|
|
|
lundi 26 novembre 2018 à 01h37
|
Merci, je vais analyser ton code !
J'avais remarqué que 2834329 était premier. Peut-être que tous les entiers renvoyés sont premiers (même si ce serait étonnant) ?
Je ne sais pas s'il est possi…
|
|
|
dimanche 25 novembre 2018 à 23h27
|
Bonjour,
Je cherche à avoir la liste des valeurs entières du rapport suivant : 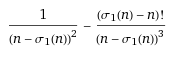
$\sigma(n)$ désigne la somme des diviseurs de n (n c…
|
|
|
dimanche 29 avril 2018 à 19h43
|
Je vois, je ne pensais pas que ça allait être si difficile. Merci pour le lien.
|
|
|
dimanche 29 avril 2018 à 19h20
|
Je viens de voir ton edit, tu es sûr pour la convergence vers 1 ? Car avec les 17 000 premiers termes je trouve déjà 1.02
|
|
|
dimanche 29 avril 2018 à 19h01
|
J'avais pensé que comme p(n) > n ln(n) alors le dénominateur serait toujours plus petit que celui avec la suite des nombres premiers et donc la convergence obtenue serait plus grande que celle obtenu…
|
|
|
dimanche 29 avril 2018 à 18h54
|
Oui c'est trouver la limite.
|
|
|
dimanche 29 avril 2018 à 18h16
|
Ok. Et avec l'approximation n ln(n) il y a moyen de sortir une convergence ? Du coup la convergence avec la suite des nombres premiers sera inférieure à celle obtenue avec n ln(n).
Après ça reste…
|
|
|
dimanche 29 avril 2018 à 18h00
|
Ah oui. Sinon il n'y a pas moyen en remplaçant par la formule qui donne exactement le nième nombre premier que j'ai postée plus haut ? Ou avec les encadrements ?
|
|
|
dimanche 29 avril 2018 à 17h43
|
Merci.
Du coup j'ai du mal à voir ce que donnerait l'expression à étudier car ce que tu donnes fournit directement la somme des n premiers nombres premiers (je pense qu'on peut l'utiliser aussi qu…
|
|
|
dimanche 29 avril 2018 à 16h37
|
Bonjour,
J'essaye de trouver la convergence de la suite $\frac{1}{2} + \frac{1}{5} + \frac{1}{10} + \frac{1}{17} + \frac{1}{28} + ...$
À chaque fois au dénominateur on ajoute le nombre premier qu…
|
|
|
mercredi 08 novembre 2017 à 23h11
|
> Comme Lucas, je me demande où tu en es de tes réflexions ; je n'ai rien compris à ton message d'hier soir.
>
> Il y a une accumulation d'imprécisions : nombres entiers naturels (donc positifs),…
|
|
|
mercredi 08 novembre 2017 à 22h47
|
Une forme qui donnerait les couples (x;y) qui conviennent pour ne tomber que sur des nombres premiers finissant par 7. Par exemple (x;y) = (-1;-4) convient.
|
|
|
mercredi 08 novembre 2017 à 22h25
|
> > La 1ère exression permet de génerer tous les entiers positifs finissant par 7. ( c'est probablement l'étape la plus difficile à démontrer, est-ce qu'on couvre bien tous les nombres qui finissnet …
|