@InaDeepThink : Je ne comprends pas ta question, par "séparer" je n’entends pas "union", je ne vois pas quel sens ça aurait. Par exemple avec 1 ligne, on peut séparer le plan en 2. Avec 2 lignes, on peut séparer le plan en 4. Avec 3 lignes, on peut séparer le plan en 7. (Presque les premières puissances de $2$.)
Il faut :
Trouver une formule donnant le nombre de régions délimitées par $n$ hyperplans dans $ℝ^k$ (en position générale). Lui ajouter le nombre de sous-espaces qui s’obtiennent comme intersection de certains de ces hyperplans.
Trouver une formule donnant pour $k$ élèves et $n$ lancers permis, le nombre maximal d’étages qu’il est possible de tester.
Trouver une interprétation de pourquoi ça donne la même formule.
Oh, on m’a montré un problème marrant aujourd’hui, il est sûrement déjà passé sur le sdz mais pas ici donc je le pose :
Problème 25: je dispose d’un polynôme à coefficients entiers et positifs, votre but est de trouver ce polynôme. Pour cela, vous avez le droit de me demander deux fois l’image d’un réel de votre choix par ce polynôme (exemple: vous me demandez P(pi) puis P(54)).
Quelle est la démarche à suivre pour gagner à tous les coups ?
Question bonus, le problème est le même mais doit être résolu de tête, sans faire appel à une calculette ou autre.
Ok, le problème est sympa
Juste @blo yhg, ne poste surtout pas une solution à ton problème, car j’ai pas eu le temps mais je veux absolument le chercher
$k = P(1)$ (on obtient donc la somme des coefficients de $P$). On note $s$ le nombre de chiffres de $k$.
Ensuite on demande gentiment : $P(10^{s+1})$. On obtient alors : $\displaystyle \sum_{k = 0}^{n} a_k \cdot 10^{sk+k}$, donc puisque le coefficent devant $a_{k+1}$ est : $10^{(sk+k)+s+1}$ et que chacun des $a_k$ est positif et à un nombre de chiffres strictement inférieur à $s$, on peut bien identifier dans $P(10^{s+1})$ les coefficients.
Peut-être qu’il faut pouvoir donner la liste des coefficients directement quand on nous donne les réponses dans notre manière habituelle de représenter les nombres, comme le fait la réponse de InaDeepThink ? Mais bon ça reste idéalisé quand même suivant le polynôme.
Je trouve ça plus rigolo formulé comme « le nombre minimum d’évaluations pour déterminer le polynôme », sans spoiler ce nombre.
Tout à fait, mais ça n’est plus la même question alors, ça change la réponse (bon peut-être pas pour la question bonus). Et même que la réponse est dans le message de melepe, donc non je ne triche pas.
Juste @blo yhg, ne poste surtout pas une solution à ton problème, car j’ai pas eu le temps mais je veux absolument le chercher
Généralement quand on résout le problème on a l’idée de demander P(1), puis (P(P(1) + 1), et alors les coefficients sont affichés en base P(1) + 1. Sauf que donner des coefficients en base P(P(1) + 1) c’est pas intuitif, on préfère les coefficients en base 10. Pour ça, évaluer P à la puissance de 10 directement supérieure à P(1) te donne les coefficients en base 10 (et donc tu n’as pas besoin de faire des changements de base calculatoires).
Je signale juste que j’ai fait une erreur dans l’énigme que j’ai donnée en lien avec le problème du jeter d’étudiants (merci à InaDeepThink). La version correcte était la première : on ne doit pas ajouter le nombre de sous-espaces obtenus comme intersection de certains des $n$ hyperplans.
Le problème que j’avais considéré quand j’ai vérifié ce que je disais de mémoire n’était pas le bon : j’ai considéré que quand on jette un étudiant d’un étage, on obtient l’information de si l’étage critique est égal, plus petit ou plus grand que l’étage du jeter. Avec cette version, il faut bien ajouter les sous-espaces. L’interprétation géométrique fonctionne pour les deux versions.
Bon, je pense que blog yhg avait une bien meilleur idée en tête, mais voilà l’idée que j’avais.
Rappelons rapidement les conditions, pour partir sur une même compréhension du problème qui est posé. On peut jeter un étudiant d’une fenêtre et celui-ci peut soit mourir soit survivre, si il meurt on a un étudiant en moins, si il survit on peut le réutiliser.
On essaie de déterminer l’immeuble le plus grand possible (en nombre d’étages) tels qu’il est possible avec $n$ lancés de déterminer, l’étage fatal de cet immeuble, tels que :
dans tous les cas le dernier étage de l’immeuble est fatal, donc si un immeuble à $m$ étages et qu’un étudiant suivit au à tous les étages $ \leq m-1$ alors on peut directement en déduire que le $m$-ième étage est fatal.
si l’étudiant survit à tous les étages de l’immeuble alors le premier étage est fatal, puisqu’on considère que dans un immeuble dans tous les cas au moins un étage est fatal.
Ceci étant dit, commençons par trouver une formule donnant le nombre maximal d’étage que peut avoir un immeuble si on nous donne $k$ étudiants et $n$ lancés.
On note $f : \mathbb{Z}^2 \rightarrow \mathbb{N}$ la fonction, qui à tout couples de la forme : $($nombre d’étudiants, nombre de lancés$)$ associe le nombre d’étages maximal qu’on peut obtenir.
Par exemple : $\forall k \in \mathbb{N}^*, f(k,1) = 2$, avec la convention : $f(a, b) = 0$ si $a \leq 0$ ou bien si $b \leq 0$.
Si on a $n+1$ lancés, remarquons qu’on a alors : $f(k, n+1) = f(k-1, n)+f(k, n)$. Effectivement, lorsqu’on lance notre premier étudiant d’un étage , soit il meurt et dans ce cas là il nous reste $n$ lancés et $k-1$ étudiants, donc on se retrouve à calculer $f(k-1, n)$, ou bien il survit et dans ce cas on se retrouve donc à calculer $f(k, n)$. On a donc $f(k, n+1) = f(k-1, n) + f(k, n)$ (on notera que c’est bien une somme disjointe car si l’étudiant survit alors on doit déterminer le nombre d’étages que l’on peut obtenir "au dessus", et si il meurt on doit déterminer le nombre d’étages "en-dessous").
En utilisant la condition initiale, $ \forall k \in \mathbb{N}^*, f(k, 1) = 2$ on trouve (c’est pas trop compliqué, je mettrai dans la semaine les détails des calculs) :
Essayons de prouver que c’est la même formule qui donne le nombre de régions délimités par $n$-hyperplan, en comprenant le lien avec les étudiants et l’immeuble.
2.
Introduisons la relation d’équivalence : $\sim$, on dira que deux mots $a$, $b$ sur l’alphabet $\{0, 1\}$ sont tels que $ a \sim b$ si et seulement si :
si $a = b$
ou bien si $a = m \overbrace{0 \ldots 0}^{k \text{ fois }} c$ et $b = m \overbrace{0 \ldots 0}^{k \text{ fois }} d$ ou $m \in \sum^*$ et $c, d \in \sum^{+}$.
On a alors : $f(k, n) = \sup\{ \mid E \mid : E \subset \sum^+, \forall m \in E, \mid m \mid = n, \not\exists a, b \in E, a \sim b \} = \mid E/\sim \mid $.
En fait, ce résultat se voit si on représente $0$ comme un étudiant qui meurt et $1$ comme un étudiant qui survit. Si on se trouve dans un immeuble à $m$ étages et que l’on arrive à déterminer quel étage est fatal, ça veut dire qu’on arrive à trouver un mot binaire nous permettant de trouver cet étage, soit une succession de $n$ lancés étudiants qui soit valide.
Par exemple prenons le cas ou $(n, k) = (2,2)$ , dans ce cas là on peut avoir au maximum $4$ étages. Supposons que l’étage fatal soit l’étage numéro $2$.
Bon on commence par jeter un étudiant au deuxième étage, il meurt on a donc pour l’instant le mot $0$. Ensuite on jette le dernier étudiant qu’il reste au premier étage, cet étudiant survit et on en déduit que le deuxième étage est fatal grâce au mot $01$.
Maintenant, il faut comprendre que la relation d’équivalence introduite est très importante. En effet elle s’assure de supprimer les suites non valides. Si on a $k$ fois le caractère $0$ dans une de nos suites, ça veut dire que $k$ étudiants meurent, mais dans ce cas il est impossible de jeter plus d’étudiants puisqu’ils sont tous morts, donc les caractères qu’il y a derrière ces $k$$0$, ne servent à rien, ainsi c’est pourquoi on "identifie" ces mots à un seul puisqu’un de ces mots détermine un seul étage.
On comprend mieux pourquoi, $f(n, k)$ est égal à l’ensemble des classes d’équivalences de $E$ par $ \sim$, effectivement, qu’importe ou se trouve l’étage fatal on doit avoir une suite de $0$ et de $1$ (donc une suite d’étudiants qui meurent ou survivent) de taille $n$ (on a que $n$ lancés) tels qu’il est possible d’identifier cet étage, on a donc bien : $f(n, k) = \mid E / \sim \mid$, ou $E = \{m \in \sum^+ \mid \mid m \mid = n\}$ .
A partir de cette nouvel "visualisation" du problème (comme le cardinal de l’ensemble des classes équivalences d’un ensemble par une relation bien choisit), on va mieux comprendre le lien avec $2.$.
Effectivement on va montrer que le nombre de régions délimitées par ces $n$ hyperplans, détermine exactement ce cardinal.
On commence par noté $g:\mathbb{Z}^2 \rightarrow \mathbb{Z}$ la fonction qui à un couple donne le nombre de régions que l’on peut délimité dans $\mathbb{R}^k$ avec $n$ hyperplans.
Maintenant on peut identifier un lancé à un hyperplan, et une intersection à une suite. A chaque fois qu’un hyperplan sépare l’espace en deux parties on peut associer ces deux parties à : l’une représente le cas ou un étudiant meurt et l’autre à celle ou il survit.
Pour $(n, k) = (2, 2)$ on peut donc avoir la figure suivante :
On remarque que pour des petites valeurs de $k$, on a un lien entre le cardinal de $E/\sim$ et $g(k, n)$, on va essayer de comprendre pourquoi c’est vrai pour des valeurs plus grandes.
Maintenant l’idée c’est que lorsqu’on rajoute un hyperplan, pour maximiser le nombre de régions il faut clairement que cet hyperplan intersecte tous les hyperplans déjà en place, on rajoute alors un $1$ à chacun de ceux-ci (on a alors des mots de $n+1$ caractères).
Pour les autres nouvelles régions délimitées, on y rajoute à $0$, mais il faut savoir lesquelles peuvent obtenir un $0$ (càd faire mourir un étudiant), or ce nombre est tout simplement de $f(k-1, n)$, puisque c’est le nombre d’anciennes régions se terminant n’ayant pas encore de sous mots avec $k$$0$.
Ainsi en gros, un hyperplan représente le lancé d’un étudiant, on peut lire l’intersection des hyperplans comme une suite de $0$ et de $1$, tels que le $0$ représente la mort d’un étudiant et le $1$ la survit de celui-ci. Lors de l’ajout d’un hyperplan, si l’on veut maximiser le nombre de région il faut que ce nouvel hyperplan intersecte tous les autres hyperplans déjà en place, en bref ce $n+1$ième hyperplan coupe l’espace en deux, d’un côté on a l’espace d’origine (même nombre de région), cela correspond au cas ou on rajoute un $1$, car le lancé du $n+1$ième étudiant survit, et dans le cas ou il meurt on a exactement le nombre de régions délimités par $n$ hyperplans dans $\mathbb{R}^{k-1}$ (ça se voit assez bien sur un dessin, même si pour $k \geq 3$ c’est un peu plus chaud :D), ainsi on rajoute un $0$ à l’ensemble des mots n’ayant pas $k$$0$ comme sous mot et qui ne sont pas égaux par $\sim$.
Donc on a clairement : $g(n,k) = \mid E/\sim \mid$
Je me permet de directement de proposer un nouveau problème car ça fait longtemps qu’on en a pas proposé un:D
On prend trois points au hasard sur une sphère. Quelle est la probabilité que les cordes qui les joignent forment un triangle acutangle ?
J’ai lu un peu plus en détail et en fait non, ce n’est pas comme je faisais.
si l’étudiant survit à tous les étages de l’immeuble alors le premier étage est fatal, puisqu’on considère que dans un immeuble dans tous les cas au moins un étage est fatal.
Y’a un bug là, tu voulais peut-être dire que si tous les étages sont fatals, alors c’est le premier étage qu’il faut considérer comme critique (c’est en quelque sorte le dual du premier point si on imagine que les « étages négatifs » ne sont jamais fataux… et puis mince j’ai eu envie d’écrire fataux alors voilà !).
J’utilise bien la même récurrence pour le calcul de $f(k,n)$. Je ne sais pas si tu connais mais les séries formelles permettent de rédiger la preuve de manière efficace.
Pour ta présentation avec les mots binaires en fait je ne comprends pas ce que tu fais. C’est quoi intuitivement, ta relation d’équivalence ? Déjà j’ai l’impression que tu voulais plutôt dire que $a$ et $b$ sont équivalents si ils sont égaux ou que leur plus grand préfixe commun a au plus $k$ occurences de $0$, non ? Il ne faut pas forcer les $0$ soient consécutifs, n’est-ce pas ? Mais même en réinterprétant ainsi, je ne vois pas.
Si ce que tu veux faire, c’est considérer l’ensemble $E_{k,n}$ des mots qui apparaissent comme séquence de « mort, pas mort, pas mort, mort, etc. » quand on effectue les lancers, ça m’a l’air intéressant mais aussi un peu complexe… En notant $∗$ la concaténation et $+$ l’union (notations comme pour les langages formels), ça donne comme récurrence $E_{k,n} = 1 ∗ E_{k-1,n-1} + 0 ∗ E_{k,n-1}$. Par exemple on a :
$E_{1,4} = \{1,01,001,0001,0000\}$,
$E_{2,3} = \{11,101,100,011,010,001,000\}$.
Peut-être que j’ai manqué quelque chose mais je ne vois pas de description simple de $E_{k,n}$.
edit$E_{k,n}$ est l’ensemble des mots de longueur $n$ et de poids de Hamming au plus $k$, peut-être que c’est ce que tu disais. Ça donne en même temps une preuve de la formule pour $f(k,n)$ (que je ne détaille pas). Il faudra que je regarde mieux ce qu’on peut faire avec, je n’ai pas compris ce que tu as rédigé.
edit J’ai la flemme de continuer mais on fait la même chose dite différemment. Moi j’identifiais directement les étages aux région par une récurrence, sans passer par les mots binaires.
Tout d’abord, si on choisit trois points au hasard sur un sphère, alors l’intersection du plan passant par ces trois points et de la sphère forme un cercle. On peut donc se restreindre au cercle. Je fais alors appel à la figure suivante :
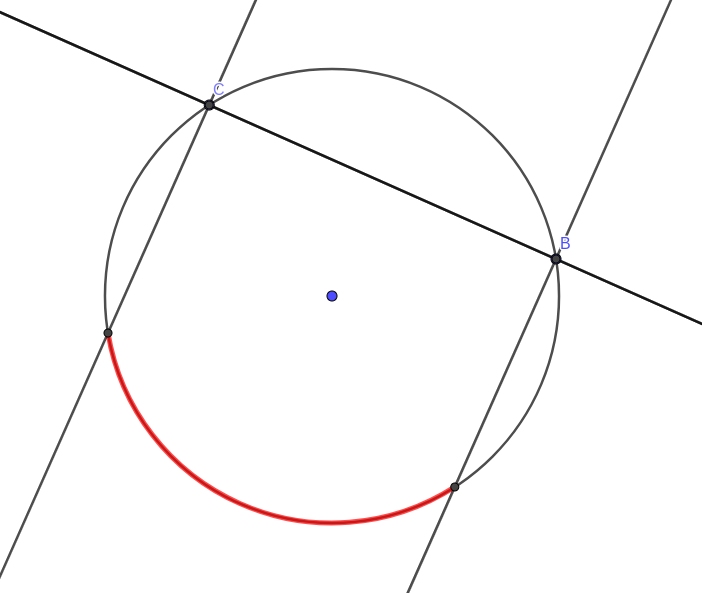L’idée est la suivante : si je choisis deux points aléatoirement sur le cercle, quelle est la probabilité qu’en choisissant le troisième point, le traingle formé est acutangle ? J’ai donc les points $B$ et $C$. Si on trimbale un point $D$ sur le cercle, on voit bien que le seul arc sur lequel il répond au problème est l’arc rouge. On observe un angle obtus sinon.
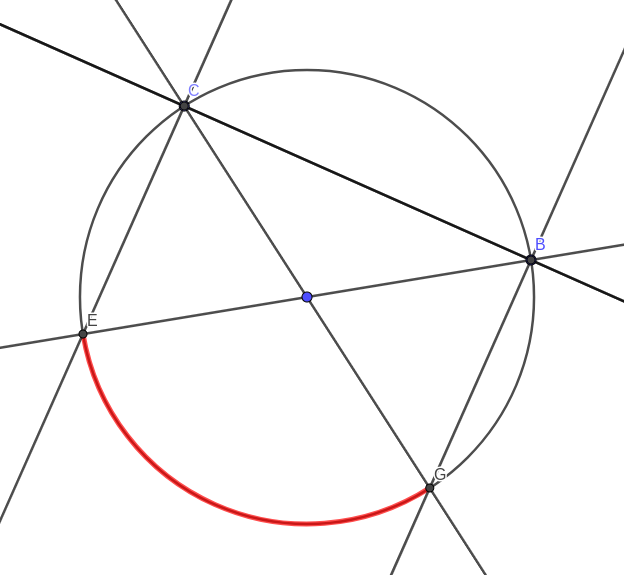Par construction $BCEG$ forme un rectangle, donc $\widehat{EOG} = \widehat{BOC}$. Ensuite il n’y a plus qu’à se demander quel est l’angle moyen $\widehat{BOC}$ : on place au hasard le premier point, et le deuxième point forme avec lui un angle entre $0$ et $180°$, donc en moyenne $90°$. Cela veut dire que, ayant placé les deux premiers points, il y a en moyenne une chance sur quatre que les trois points forment un triangle acutangle. Donc la probabilité est de $\frac{1}{4}$.
NB : pour la dernière étape, on peut le justifier comme suivant : si $X$ est la variable aléatoire qui vaut $1$ lorsque le triangle est acutangle et $0$ sinon, et $Y$ la mesure de l’arc entre les deux premiers points, alors on sait que :
Le résultat n’est pas correct. Je pense que le problème vient du fait que tu admets que les angles du triangle $ABC$ sont répartis au hasard comme si les sommets étais choisis de façon équiprobable sur le cercle circonscrit.
Quand on calcule expérimentalement la probabilité conditionnelle de tomber sur un triangle aigu sachant qu’on est dans une petite bande autour d’un cercle sur la sphère (n’importe lequel), c’est toujours très proche de $1/4$ (flemme de conditionner pour que le cercle soit compris en entier dans la bande). Ça c’est normal. Mais si on passe à la sphère toute entière, on trouve une autre valeur ! Ça donne un contre exemple à ce qu’il y a écrit sur wikipédia et qui est probablement une bêtise… je ne trouve rien sur cette idée d’approcher une probabilité conditionnelle de cette manière, pourtant c’est quelque chose qui semble assez intuitif.
Voici un autre exemple reprenant la même idée mais en 2d. On tire deux points dans le disque unité, uniformément selon la mesure de Lebesgue. On considère la corde passant par ces deux points et on regarde la probabilité que la distance séparant les deux points soit supérieure ou égale à la moitié de la longueur totale de la corde.
Si on prend deux points uniformément répartis sur une corde du cercle, on trouve $1/4$. Pourtant, expérimentalement, on trouve $1/2$ si on prend deux points dans le disque. Fixons $𝜀>0$ très petit et pour chaque corde du cercle, on regarde une zone d’épaisseur $𝜀$ autour de cette corde. Quand on conditionne par « être dans cette zone », on obtient comme probabilité $1/4$ (lorsque $𝜀$ tend vers $0$). Si on tire nos deux points en commençant par tirer une corde selon la bonne loi puis en tirant deux points uniformément dans la bande autour de cette corde, on va trouver comme probabilité $1/4$ pour notre proposition. Mais le problème est que les configurations où les deux points sont proches vont être sur-représentées car les vont être compris dans beaucoup plus de bandes lorsqu’ils sont proches que lorsqu’ils sont loin. C’est cohérent avec le fait que l’on sous-estime ainsi la probabilité : quand les points sont proches, la propriété a tendance à ne pas être vérifiée.
Ça fait penser au paradoxe de Borel, dans lequel on fait la même approximation.
@InaDeepThink Tu attends une méthode sans trop de calcul ?
Normalement oui, il n’y a pas trop trop de calculs, juste une intégrale Par contre si on veut voir la correspondance entre ces différentes distributions de probabilités il peut y avoir rapidement beaucoup de calculs.
Soit $A,B,C$ les trois points et soit $O$ l’origine. On conditionne par $A$ et on effectue une rotation ramenant $A$ à l’origine, les deux autres points sont indépendants et uniformément répartis. On conditionne par $B$. La densité de probabilité d’obtenir un angle $\angle AOB$ (non orienté) de $𝜃$ est proportionnelle à la longueur du cercle correspondant, soit proportionnelle à $\sin(𝜃)$. L’intégrale de $\sin(𝜃)$ de $0$ à $𝜋$ est $2$, donc la densité est $\sin(𝜃)/2$.
Ensuite on regarde sur un dessin, pour $A$ et $B$ fixés, la zone de la sphère dans laquelle peut se situer $C$ pour que $ABC$ soit acutangle. Soit $𝜃$ l’angle non orienté $\angle AOB$. La zone recherchée est la sphère à laquelle on a retiré trois secteurs sphériques, l’un d’angle $𝜃$ et les deux autres d’angles $𝜋-𝜃$. La probabilité de tomber dans l’un de ces secteurs sphériques est
Et wolframalpha dit que ça vaut $1/2$… je le crois (pour moi c’est beaucoup de calculs ). De toute manière c’est ce que j’ai vérifié expérimentalement.
Si tu veux avoir plus d’info sur le problème et notamment sur les différentes distributions de probabilités tu peux regarder Ici, l’erreur faite par Skodt est d’ailleurs exactement celle dont la "remarque" parle.
Connectez-vous pour pouvoir poster un message.
Connexion
Pas encore membre ?
Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte
Juste @blo yhg, ne poste surtout pas une solution à ton problème, car j’ai pas eu le temps mais je veux absolument le chercher 
L’idée est la suivante : si je choisis deux points aléatoirement sur le cercle, quelle est la probabilité qu’en choisissant le troisième point, le traingle formé est acutangle ? J’ai donc les points $B$ et $C$. Si on trimbale un point $D$ sur le cercle, on voit bien que le seul arc sur lequel il répond au problème est l’arc rouge. On observe un angle obtus sinon.
Par construction $BCEG$ forme un rectangle, donc $\widehat{EOG} = \widehat{BOC}$. Ensuite il n’y a plus qu’à se demander quel est l’angle moyen $\widehat{BOC}$ : on place au hasard le premier point, et le deuxième point forme avec lui un angle entre $0$ et $180°$, donc en moyenne $90°$. Cela veut dire que, ayant placé les deux premiers points, il y a en moyenne une chance sur quatre que les trois points forment un triangle acutangle. Donc la probabilité est de $\frac{1}{4}$.
NB : pour la dernière étape, on peut le justifier comme suivant : si $X$ est la variable aléatoire qui vaut $1$ lorsque le triangle est acutangle et $0$ sinon, et $Y$ la mesure de l’arc entre les deux premiers points, alors on sait que :
). De toute manière c’est ce que j’ai vérifié expérimentalement.
