L'inertie selon Aristote
Prenez un objet et faites-le glisser sur la table devant vous. Qu'observez-vous ? L'objet continue son mouvement, puis finit par s'arrêter. Pourquoi ? Facile, me direz-vous, c'est à cause des forces de frottement. Imaginons d'ailleurs une table beaucoup plus lisse, l'objet ira beaucoup plus loin.
Mais si nous supprimions totalement les frottements, que se passerait-il ? L'objet continuerait-il son mouvement indéfiniment ? (en supposant une table de dimension infinie)
Je sens une pointe d'hésitation en vous. Imaginer un mouvement infini ne va pas de soi. Il faudra d'ailleurs attendre Galilée pour exprimer une telle loi.
Quelle était la situation avant lui ? La physique au Moyen-âge est dominée par les écrits d'un homme : Aristote (384-322 av. JC). Dans sa Physique, il décrit son système du monde, basé sur les quatre éléments et la notion de lieu naturel. Chaque élément a son lieu naturel, vers lequel il tend toujours : l'eau et la terre (et donc tout objet solide) tendent vers le bas, le feu et l'air tendent vers le haut. Tout autre mouvement est un mouvement contraint, nécessitant l'action d'une force.
Quelle est précisément l'action d'une telle force ? Si on lance un objet, on lui fournit un impetus, qui lui fournit une certaine vitesse. L'objet va conserver cette vitesse jusqu'à ce qu'il ait consommé tout son impetus.

À ce moment-là, son impetus étant épuisé, l'objet retourne vers son lieu naturel, donc vers le bas. Ainsi pour Aristote, la trajectoire d'un boulet de canon est celle décrite par le schéma ci-dessus : une partie en ligne droite, à vitesse constante, puis une partie verticale, qui ramène l'objet vers le bas.

L'inertie selon Garfield : tout corps tend vers son lieu naturel
L'inertie selon Galilée
Puis vint Galilée (1564-1642). Dans son livre Dialogue sur les deux grands systèmes du monde, il oppose deux systèmes : le système aristotélicien, géocentrique, et le système copernicien, dans lequel la Terre se meut autour du Soleil.
Or, quel est le principal argument contre le mouvement de la Terre ? Il réside justement dans la conservation du mouvement : dans le cadre aristotélicien, comment expliquer que les oiseaux puissent voler dans le ciel pendant que la terre se déplace, ou qu'un homme qui saute en l'air puisse retomber à l'endroit exact d'où il a sauté ?
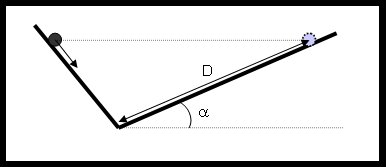
Galilée apporte une réponse, grâce à ses expériences sur les plans inclinés, qui l'amèneront au principe d'inertie : soit une bille roulant sur deux planches, comme sur le schéma ci-dessous. Galilée remarque que, quel que soit l'angle $\alpha$ , la bille revient à la hauteur à laquelle elle a été lâchée. Plus l'angle est petit, plus la bille parcourt donc une distance élevée.
Et si la deuxième planche était horizontale, se demande Galilée. Comme la bille décélère sur une pente montante, et accélère sur une pente descendante, sur une surface horizontale, elle continuerait son mouvement à vitesse constante.
" Une vitesse quelconque imprimée à un corps se conserve rigoureusement aussi longtemps que les causes extérieures d’accélération ou de ralentissement sont écartées, condition qui se réalise seulement dans le plan horizontal ; car dans les plans déclives il existe déjà une cause d’accélération, tandis que dans les plans qui montent il existe une cause de ralentissement. D’où il suit que le mouvement sur le plan horizontal est perpétuel. "
Galileo Galilei, Discours et démonstrations concernant deux sciences nouvelles (1636)
Mais c'est à ce moment qu'il commet une erreur d'appréciation. Une surface qui ne monte ni ne descend est pour lui une surface qui reste à la même altitude et qui donc…suit la surface de la Terre. Voilà l'erreur qui empêchera Galilée d'être considéré comme le père du principe d'inertie : un mouvement inertiel est pour lui un mouvement circulaire, qui suit la courbure de la Terre.
Le vrai principe d'inertie apparaîtra sous la plume de Descartes, puis de Newton. La formulation qu'en fait Descartes mérite d'être mentionnée ici. Elle lui vient, non pas de uniquement de considérations physiques, mais aussi d'arguments métaphysiques sur l'immuabilité de Dieu :
"D’où il suit que, puisqu’il a mû en plusieurs façons différentes les parties de la matière lorsqu’il les a créées, et qu’il les maintient toutes en la même façon et avec les mêmes lois quil leur a fait observer en leur création, il conserve incessamment en cette matière une égale quantité de mouvement."
René Descartes, Principes de philosophie (1633)
"Que Dieu est la première cause du mouvement, et qu'il en conserve toujours une égale quantité dans l'univers […] Que chaque partie de la matière, en particulier, continue toujours d'être en même état, pendant que la rencontre des autres ne la contraint point de changer. C'est-à-dire : si elle a quelque grosseur, elle ne deviendra jamais plus petite, sinon que les autres la divisent ; si elle est ronde ou carrée, elle ne changera jamais cette figure sans que les autres ne l'y contraignent ; si elle est arrêtée en quelque lieu, elle n'en partira jamais que les autres ne l'en chassent ; et si elle a commencé une fois à se mouvoir, elle continuera toujours avec une égale force jusques à ce que les autres l'arrêtent ou la retardent. "
René Descartes, Monde ou Traité de la lumière (1633)
Il est à noter que cette loi, aussi "innocente" qu'elle puisse paraître, suscita à l'époque bien des débats, d'ordre théologique.
Ainsi, Pascal note-t-il dans ses Pensées : "Je ne puis pardonner à Descartes ; il aurait bien voulu, dans toute sa philosophie, se pouvoir passer de Dieu ; mais il n'a pas pu s'empêcher de lui faire donner une chiquenaude, pour mettre le monde en mouvement ; après cela, il n'a plus que faire de Dieu."
L'inertie selon Newton
Pour Newton l'inertie est une force, non pas au sens moderne du terme, mais comme une force interne à l'objet, qui lui permet de résister aux changements de mouvement.
Définition III
La force qui réside dans la matière (vis infita) est le pouvoir qu'elle a de résister. C'est par cette force que tout corps persévère de lui-même dans son état actuel de repos ou de mouvement uniforme en ligne droite.
Cette force est toujours proportionnelle à la quantité de matière des corps […] On peut donner à la force qui réside dans les corps le nom très expressif de force d'inertie.
Le corps exerce cette force toutes les fois qu'il s'agit de changer son état actuel, et on peut alors la considérer sous deux différents aspects, ou comme résistante, ou comme impulsive ; comme résistante, en tant que le corps s'oppose à la force qui tend à lui faire changer d'état; comme impulsive, en tant que le même corps fait effort pour changer l'état de l'obstacle qui lui résiste.
On attribue communément la résistance aux corps en repos, et la force impulsive à ceux qui se meuvent ; mais le mouvement et le repos, tels qu'on les conçoit communément, ne sont que respectifs ; car les corps qu'on croit en repos ne sont pas toujours dans un repos absolu.
Note: ce n'est plus ainsi qu'on définit l'inertie de nos jours, ce n’est pas une force. La notion de force d'inertie existe toujours, mais n'a plus le même sens (voir chapitre sur les référentiels)
"Cette force est toujours proportionnelle à la quantité de matière des corps", dit Newton. En effet, l'inertie caractérise la tendance de l'objet à conserver sa quantité de mouvement, qui est proportionnelle à la masse. Vous pouvez d'ailleurs le remarquer très facilement : à vitesse égale, vous aurez plus de mal à arrêter une boule de bowling qu'une balle de tennis.
Exit donc la notion d'impetus d'Aristote. Le mouvement uniforme et le repos ne sont plus deux états séparés de la matière, l'un n'est pas plus naturel que l'autre, un corps en mouvement ne cherche pas spontanément à revenir à son "état naturel" de repos.
Ainsi, dit Newton, "les projectiles par eux-mêmes persévèrent dans leur mouvement, mais la résistance de l'air les retarde, et la force de gravité les porte vers la terre."
De plus, il rajoute: "Une toupie, dont les parties se détournent continuellement de la ligne droite par leur cohérence réciproque, ne cesse de tourner, que parce que la résistance de l'air la retarde peu à peu.". Un lecteur moderne verra dans cet exemple la notion de conservation du moment cinétique de la toupie, mais Newton ne différencie pas ces deux lois de conservation.
Pour clore ce chapitre, analysons deux exemples :
- Imaginez une voiture au repos : elle démarre. Que ressentez-vous ? Vous vous sentez "tiré vers l'arrière" et vous vous enfoncez dans votre siège. En réalité, que s'est-il passé ? Votre corps, qui était au repos, tend à rester au repos, et oppose donc une résistance à l'accélération de la voiture. En réalité, vous n'êtes pas tiré vers l'arrière mais plutôt poussé vers l'avant par le siège de la voiture. Il se passe exactement la même chose lorsque la voiture accélère (votre corps tend à rester à vitesse constante, et la voiture vous pousse à accélérer)
- Maintenant, prenons l'exemple inverse, la voiture ralentit : vous vous sentez propulsé vers l'avant, et sans la ceinture, vous risquez de vous encastrer dans le pare-brise… En réalité c'est votre inertie qui tend à vous faire conserver la vitesse que vous aviez, alors que la voiture ralentit.