L'art de la guerre
Une des principales applications de la mécanique à l'époque de Newton était militaire : il s'agissait de la balistique. La maîtrise de la trajectoire d'un boulet de canon pouvait décider de l'issue d'une bataille, voire d'une guerre…
Cette science est donc en effervescence à l'époque, comme en témoignent quelques ouvrages : The Genuine Use and Effect of the Gunne (Robert Anderson, 1674) ou L'art de lancer des bombes (François Blondel, 1683). Mais tous ces ouvrages se basent sur les travaux de Galilée : celui-ci avait montré qu'un mouvement balistique pouvait se décomposer en un mouvement horizontal uniforme (mouvement inertiel) et un mouvement vertical uniformément accéléré. Il avait démontré à partir de là que la trajectoire était parabolique.
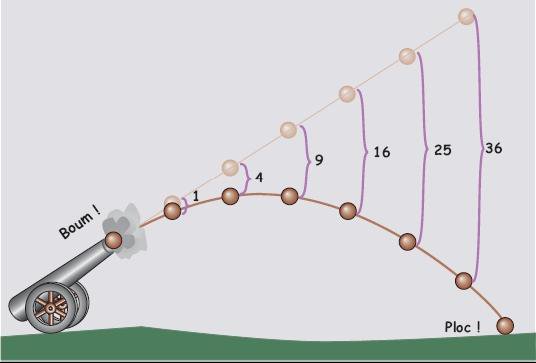
Hélas, ces travaux étaient bien insuffisants. Tous se rendaient bien compte que la trajectoire réelle était perturbée par la résistance de l'air, mais personne n'avait encore réussi à la calculer.
Newton va s'atteler à la tâche : sa troisième loi va permettre enfin de dompter cette résistance.
L'air fait de la résistance
D'où vient cette résistance, se demande Newton ? Elle provient des chocs entre le projectile et l'air ambiant. Or nous avons vu qu'en corollaire de sa loi de l'action et de la réaction apparaissait la loi de conservation de la quantité de mouvement. L'objet, en se déplaçant, va transmettre une partie de sa quantité de mouvement à l'air ambiant. Or d'après la loi de conservation, il doit perdre cette même quantité de mouvement. La perte de vitesse est donc proportionnelle à la vitesse de l'objet.
Mais ce n'est pas tout : la quantité de mouvement perdue est aussi proportionnelle à la masse d'air qui a été déplacée. Or, plus l'objet va vite, plus il rencontre d'air en un temps donné : s'il va deux fois plus vite, il transmet donc deux fois plus de vitesse à deux fois plus d'air…
Ainsi, la quantité de mouvement perdue est deux fois proportionnelle à la vitesse.
Elle est donc proportionnelle au carré de la vitesse.
Il en est donc de même pour la force motrice (qui est ici la résistance de l'air).
Citons Newton une dernière fois, pour voir comment il nous le présente :

Comme il l'annonce, il va donc s'atteler à la détermination du mouvement. Le développement mathématique de ce problème est malheureusement trop technique pour être présenté dans ce cours : Newton utilise un langage géométrique et ses démonstrations font appel à des résultats comme la quadrature de l'hyperbole par exemple. Sachez que ce problème se résout aujourd'hui par ce qu'on appelle une équation différentielle (la quadrature de l'hyperbole faisant appel à la notion d'intégrale). Et cette branche des mathématiques (le calcul infinitésimal), qui elle aussi va révolutionner la science, sera inventée entre autres par… Isaac Newton lui-même.