Est reproduite ici la démonstration de Galilée concernant la chute des corps. Il y démontre qu’un objet subissant une accélération constante parcourt une distance proportionnelle au carré du temps. Employant un raisonnement géométrique, il utilise ce qu’on appelle la méthode des indivisibles, qui permet de calculer des aires en les divisant en surfaces infiniment petites. Vous reconnaîtrez sûrement là les prémisses du calcul intégral, utilisé aujourd’hui pour démontrer un tel résultat.
Théorème I - Proposition I
Théorème I - Proposition I
Le temps pendant lequel un espace donné est franchi par un mobile, partant du repos, avec un mouvement uniformément accéléré, est égal au temps pendant lequel le même espace serait franchi par le même mobile avec un mouvement uniforme, dont le degré de vitesse serait la moitié du plus grand et dernier degré de vitesse atteint au cours du précédent mouvement uniformément accéléré.

Représentons par la ligne AB le temps pendant lequel un mobile, partant du repos en C, franchira d'un mouvement uniformément accéléré l'espace CD; on représentera le plus grand et dernier des degrés de la vitesse accrue dans les instants du temps AB par la ligne EB, formant avec AB un angle droit; menons AE: toutes les lignes parallèles à BE, tirées des différents points de la ligne AB, représenteront les degrés de vitesse croissants après l'instant initial A.
Divisons BE en son milieu par le point F, et menons FG et AG respectivement parallèles à AB et FB; on aura construit le rectangle AGFB égal au triangle AEB, et dont le côté GF coupe AE en son milieu I; si ensuite les parallèles du triangle AEB sont prolongées jusqu'à GI, nous aurons l'agrégat de toutes les parallèles contenues dans le quadrilatère égal à l'agrégat des parallèles comprises dans le triangle AEB; en effet celles qui se trouvent dans le triangle IEF correspondent à celles que contient le triangle GIA, et celles qui sont dans le trapèze AIFB sont communes.
Comme d'autre part à tous les instants, pris un à un, de l'intervalle AB correspondent tous les points, pris un à un, de la ligne AB, et comme les parallèles menées à partir de ces points et comprises dans le triangle AEB représentent les degrés croissants de la vitesse grandissante, tandis que de leur côté les parallèles contenues dans le rectangle représentent autant de degrés de la vitesse non croissante, mais égale, il est clair qu'autant de moments de vitesse seront consumés dans le mouvement accélérés d'après les parallèles croissantes du triangle AEB, que dans le mouvement uniforme d'après les parallèles du rectangle GB; en effet, ceux des moments qui font défaut dans la première moitié du mouvement accéléré (c'est-à-dire ceux qui sont représentés par les parallèles du triangle AGI) sont compensés par les moments que représentent les parallèles du triangle IEF.
Il est donc manifeste que des distances égales seront parcourues en un même temps par deux mobiles dont l'un, partant du repos, se meut d'un mouvement uniformément accéléré, et l'autre d'un mouvement uniforme que caractérise un moment de vitesse égal à la moitié du plus grand moment de vitesse atteint par le premier. C.Q.F.D.
Théorème II - Proposition II
Théorème II - Proposition II
Si un mobile, partant du repos, tombe avec un mouvement uniformément accéléré, les espaces parcourus en des temps quelconques par ce même mobile sont entre eux en raison double des temps, c'est-à-dire comme les carrés de ces mêmes temps.
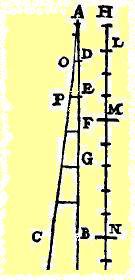
Convenons de représenter par la ligne AB un flux de temps avec un premier instant A, et soient AD et DE deux intervalles quelconques pris dans ce temps; soit la ligne HI le long de laquelle le mobile, partant du repos en H, descendra d'un mouvement uniformément accéléré; soit encore HL l'espace franchi pendant le premier intervalle de temps AD, et HM l'espace franchi pendant l'intervalle AE. Je dis que le rapport de l'espace HM à l'espace HL est en raison double de celui que le temps AE a au temps AD, ou encore que les espaces HM et HL ont même rapport que les carrés de AE et AD.
Traçons la ligne AC, faisant avec AB un angle quelconque. Des points D et E menons les parallèles DO et EP: DO représentera le plus grand degré de la vitesse acquise à l'instant D de l'intervalle de temps AD, et EP le plus grand degré de la vitesse acquise à l'instant E de l'intervalle de temps AE.
Mais on a démontré plus haut (Th. 1), à propos des espaces parcourus, que sont égaux des espaces dont l'un est parcouru par un mobile se mouvant à partir du repos avec un mouvement uniformément accéléré, alors que l'autre, durant le même intervalle de temps, est parcouru par un mobile mû d'un mouvement uniforme dont la vitesse est la moitié de la plus grande vitesse acquise dans le mouvement accéléré.
Il en découle que les distances HM et HL sont identiques à celles qui seraient traversées dans les intervalles de temps AE et AD, par des mouvements uniformes dont les vitesses seraient comme la moitié de EP et DO respectivement. Si donc on parvient à montrer que les espaces HM et HL sont en raison double des temps EA et DA, la proposition sera établie.
Or il a été démontré, dans la proposition 4 du livre 1, que les espaces franchis par des mobiles animés d'un mouvement uniforme sont entre eux dans un rapport composé du rapport des vitesses et du rapport des temps. Dans le cas présent le rapport des vitesses est le même que le rapport des temps (en effet, le rapport de la moitié de EP à la moitié de DO, ou de EP à DO, est le même que le rapport de AE à AD), et donc le rapport des espaces traversés est bien égal au carré du rapport des temps. C.Q.F.D.
Galilée, Discours et démonstrations concernant deux sciences nouvelles