Annexe B: L'énergie

Nous allons ici redémontrer les formules de l'énergie potentielle et de l'énergie cinétique.

NB: la connaissance du calcul intégral est nécessaire pour comprendre cette partie.

L'énergie potentielle

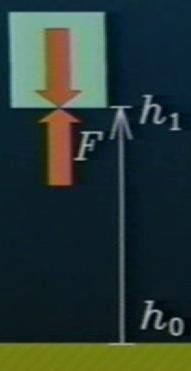
Soit donc une force soulevant un corps d'une hauteur infinitésimale $dx$. Le travail effectué est égal à:

$$ \delta W = F.dx $$

Pour quantifier l'énergie totale accumulée par le corps lorsqu'il est soulevé à la hauteur $h_1$, il nous faut intégrer cette expression:

$$W = \int^{h_1}_{0} F.dx$$
Or la force s'opposant au poids, elle est égale à $mg$. On obtient donc:
$$W = \int^{h_1}_{0} mg.dx$$

Si on note $h$ la hauteur totale, on obtient alors:

$$W = mgh$$
C'est ce qu'on appelle l'énergie potentielle, liée à la hauteur de l'objet.

Pourquoi énergie potentielle ? Parce que cette énergie peut être restituée, comme l'avait noté Leibniz dans ses expériences de pensée : lâché d'une certaine hauteur, ce corps pouvait, grâce à un système de bascule, soulever un autre corps de même masse à la même hauteur, ou un corps de masse double à une hauteur moitié moindre, etc…

Cette énergie est restituée sous forme de vitesse. Il existe donc une forme d'énergie liée à la vitesse, que nous appelons énergie cinétique. Cherchons son expression…

L'énergie cinétique

Calculons donc le travail d'une force dont l'effet est non plus de soulever un objet mais de l'accélérer. Sur une distance infinitésimale $dx$, son travail vaut:

$$ \delta W = F.dx $$

Si la force agit de $0$ à $x_1$, l'énergie accumulée vaut:

$$E_c = \int^{x_1}_{0} F.dx$$
Or d'après la deuxième loi de Newton, on a :
$$F = ma$$
On obtient donc:
$$E_c = \int^{x_1}_{0} ma.dx$$
Effectuons quelques manipulations sur cette expression:
$$E_c = \int^{x_1}_{0} m\frac{dv}{dt}.dx$$
Or, $\frac{dx}{dt}$ est égale à la vitesse. La formule revient alors à intégrer $mv$ entre $0$ et $v_1$ , la vitesse atteinte en $x_1$.
$$E_c = \int^{v_1}_{0} mv.dv$$

Ce qui nous donne, pour un objet ayant atteint une vitesse $v$:

$$E_c = \frac{1}{2}mv^2$$

Nous avons donc trouvé là l'expression de l'énergie cinétique d'un objet possédant une vitesse $v$.