Les tableaux

• Ada, les types composites
• Sommaire
• Les chaînes de caractères

Comme prévu, nous allons aborder dans ce chapitre un nouveau type de données, les tableaux ou ARRAY en Ada. Ce sera pour nous l'occasion d'aborder et d'expliquer ce que sont les types composites. Puis nous nous concentrerons sur notre premier type composite, les tableaux. À quoi cela ressemble-t-il en Ada ? Quel intérêt à faire des tableaux ? Comment faire des tableaux uni-, bi-, tridimensionnels ? Ce sera également l'occasion de réinvestir ce que nous avons vu dans la seconde partie, notamment sur les boucles.

• Les types composites, c'est quoi ?
• Tableaux unidimensionels
• Tableaux multidimensionels
• Des tableaux un peu moins contraints
• Quelques exercices
• Pour les utilisateurs de la norme Ada2012

Les types composites, c'est quoi ?

N'ayez crainte, vous pourrez continuer à suivre ce tutoriel, même si vous n'avez pas bien compris ce qu'est un type composite : toute la partie III y est consacrée. En fait, disons que si les types composites vont nous ouvrir de nombreuses portes qui nous étaient pour l'instant fermées, elle ne va pas pour autant révolutionner notre façon de coder ni remettre en cause ce que nous avons déjà vu.

Pour mieux comprendre, souvenons-nous de notre TP sur le craps. Nous avions beaucoup de variables à manipuler et donc à transmettre à chaque procédure ou fonction. Par exemple, il nous fallait une variable Dé1, une variable Dé2, une variable Hasard et peut-être même une variable SommeDés. Il aurait été plus pratique de ne manipuler qu'une seul variable (appelée MainJoueur ou Joueur) qui aurait contenu ces 4 variables. De même une variable composite Bourse aurait pu gérer la mise et la somme en dollars dont disposait le joueur.

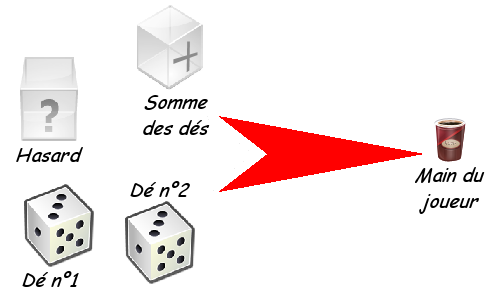
Pour schématiser, les types composites ont pour but de nous faire manipuler des objets plus complexes que de simples variables. Prenons un autre exemple, nous voudrions créer un programme qui crée des fenêtres et permet également de leur donner un titre, de les agrandir ou rétrécir… dans l'optique de le réutiliser plus tard pour créer des programmes plus ambitieux. Nous devrons alors créer notamment les variables suivantes :

• X, Y : position de la fenêtre sur l'écran
• Long,Larg : longueur et largeur de la fenêtre
• Épais : épaisseur des bords de la fenêtre
• Titre : le titre de la fenêtre
• Rfond, Vfond, Bfond : trois variables pour déterminer la couleur du fond de la fenêtre (R:rouge ; V : vert ; B : bleu)
• Actif : une variable pour savoir si la fenêtre est sélectionnée ou non
• Reduit : une variable pour savoir si la fenêtre est réduite dans la barre des tâches ou non
• …

Eh oui, ça devient complexe de gérer tout ça ! Et vous avez du vous rendre compte lors du TP que cela devient de plus en plus compliqué de gérer un grand nombre de variables (surtout quand les noms sont mal trouvés comme ci-dessus). Il serait plus simple de définir un type composite T_Fenêtre et de ne manipuler qu'une seule variable F. Imaginons également la tête de nos fonctions :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

CreerFenetre(X=>15,
             Y=>20,
             Long=>300,
             Larg=>200,
             Epais => 2, 
             Titre =>"Ma fenêtre", 
             Rfond => 20,
             Vfond => 20, 
             Bfond => 20, 
             Actif => true, 
             Reduit=> false ...)

Sans compter que, vous mis à part, personne ne connaît le nom et la signification des paramètres à moins de n'avoir lu tout le code (sans moi ). Imaginez également le chantier si l'on désirait créer une deuxième fenêtre (il faudra trouver de nouveaux noms de variable, Youpiiii !) Il serait bien plus simple de n'avoir qu'à écrire :

1
2

CreerFenetre(F) ;
ChangerNom(F,"Ma fenêtre") ; …

Nous n'aurions pas à nous soucier de tous ces paramètres et de leur nom. C'est là tout l'intérêt des types composites : nous permettre de manipuler des objets très compliqués de la manière la plus simple possible.

Tableaux unidimensionels

Problème

Le premier type composite que nous allons voir est le tableau, et pour commencer le tableau unidimensionnel, appelé ARRAY en Ada.

Les tableaux n'ont pas été créés pour nous «compliquer la vie». Comme toute chose en informatique, ils ont été inventés pour faire face à des problèmes concrets.

Voici un exemple : en vue d'un jeu (de dé, de carte ou autre) à 6 joueurs, on a besoin d'enregistrer les scores des différents participants. D'où le code suivant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

...
   ScoreJoueur1 : natural := 0 ; 
   ScoreJoueur2 : natural := 0 ; 
   ScoreJoueur3 : natural := 0 ; 
   ScoreJoueur4 : natural := 0 ; 
   ScoreJoueur5 : natural := 0 ; 
   ScoreJoueur6 : natural := 0 ; 
BEGIN
   ScoreJoueur1 :=  15 ;
   ScoreJoueur2 :=  45 ;
   ScoreJoueur3 :=  27 ; 
   ScoreJoueur4 :=  8 ; 
   ScoreJoueur5 :=  19 ; 
   ScoreJoueur6 :=  27 ; 

   get(ScoreJoueur1) ; skip_line ; 
   get(ScoreJoueur2) ; skip_line ; 
   get(ScoreJoueur3) ; skip_line ; 
   get(ScoreJoueur4) ; skip_line ; 
   get(ScoreJoueur5) ; skip_line ; 
   get(ScoreJoueur6) ; skip_line ; 
...

Un peu long et redondant, d'autant plus qu'il vaut mieux ne pas avoir besoin de rajouter ou d'enlever un joueur car nous serions obligés de revoir tout notre code ! Il serait judicieux, pour éviter de créer autant de variables, de les classer dans un tableau de la manière suivante :

Chaque case correspond au score d'un joueur, et nous n'avons besoin que d'une seule variable composite : Scores de type T_tableau. On dit que ce tableau est unidimensionnel car il a plusieurs colonnes mais une seule ligne !

Création d'un tableau en Ada

Déclaration

1

Scores : array ;

Car il existe plusieurs types de tableaux unidimensionnels : tableaux d'integer, tableaux de natural, tableaux de float, tableau de boolean, tableau de character… Il faut donc créer un type précis ! Et cela se fait de la manière suivante :

1

type T_Tableau is array of natural ;

Non je ne suis pas en plein délire, rassurez-vous. En fait, nous avons oublié lorsque nous avons écrit le tableau de numéroter les cases. Le plus évident est de le numéroter ainsi :

Il faudra donc écrire le code suivant :

1
2

Type T_Tableau is array(1..6) of integer ;
Scores : T_Tableau ;

Mais le plus souvent les informaticiens auront l'habitude de numéroter ainsi :

Il faudra alors changer notre code de la façon suivante :

1
2

Type T_Tableau is array(0..5) of integer ;
Scores : T_Tableau ;

La première case est donc la numéro 0 et la 6ème case est la numéro 5 ! C'est un peu compliqué, je sais, mais je tiens à l'évoquer car beaucoup de langages numérotent ainsi leurs tableaux sans vous laisser le choix (notamment le fameux langage C ). Bien sûr, en Ada il est possible de numéroter de 1 à 6, de 0 à 5, mais aussi de 15 à 20, de 7 à 12… il suffit pour cela de changer l'intervalle écrit dans les parenthèses.

Dernier point, il est possible en Ada d'utiliser des variables pour déclarer la taille d'un tableau, sauf que ces variables devront être… constantes !

1
2
3

TailleMax : constant natural := 5 ; 
Type T_Tableau is array(0..TailleMax) of integer ;
Scores : T_Tableau ;

Il vous sera donc impossible de créer un tableau de taille variable (pour l'instant tout du moins).

Affectation globale

Maintenant que nous avons déclaré un tableau d'entiers (Scores de type T_Tableau), encore faut-il lui affecter des valeurs. Cela peut se faire de deux façons distinctes. Première façon, la plus directe possible :

1

Scores := (15,45,27,8,19,27) ;

Simple, efficace. Chaque case du tableau a désormais une valeur. Il est également possible d'utiliser des agrégats. De quoi s'agit-il ? Le plus simple est de vous en rendre compte par vous-même sur un exemple. Nous voudrions que les cases n°1 et n°3 valent 17 et que les autres valent 0. Nous pouvons écrire :

1

Scores := (17,0,17,0,0,0) ;

Ou bien utiliser les agrégats :

1

Scores := (1|3 => 17, others => 0) ;

Autrement dit, nous utilisons une sorte de CASE pour définir les valeurs de notre tableau. Autre possibilité, définir les trois premières valeurs puis utiliser un intervalle d'indices pour les dernières valeurs.

1

Scores := (17,0,17,4..6 => 0) ;

L'ennui c'est que l'on peut être amené à manipuler des tableaux très très grands (100 cases), et que cette méthode aura vite ses limites.

Affectation valeur par valeur

C'est pourquoi on utilise souvent la seconde méthode :

1
2
3
4
5
6

Scores(1) := 15 ;
Scores(2) := 45 ; 
Scores(3) := 27 ; 
Scores(4) := 8 ; 
Scores(5) := 19 ; 
Scores(6) := 27 ;

Quand nous écrivons Scores(1), Scores(2)… il ne s'agit pas du tableau mais bien des cases du tableau. Scores(1) est la case numéro 1 du tableau Scores. Cette case réagit donc comme une variable de type Integer.

Utilisé tel quel, si ça l'est. Mais en général, on la combine avec une boucle. Disons que nous allons initialiser notre tableau pour le remplir de 0 sans utiliser les agrégats. Voici la méthode à utiliser :

1
2
3

for i in 1..6 loop
   T(i) := 0 ; 
end loop ;

L'intervalle de définition d'un type T_Tableau est très important et doit donc être respecté. Supposons que nous n'ayons pas utilisé une boucle FOR mais une boucle WHILE avec une variable i servant de compteur que nous incrémenterons nous-même de manière à tester également si la case considérée ne vaut pas déjà 0 :

1
2
3
4

while i <= 6 and T(i) /= 0 loop
   T(i) := 0 ; 
   i := i + 1 ; 
end loop ;

La portion de code ci-dessus est censée parcourir le tableau et mettre à zéro toutes les cases non-nulles du tableau. La boucle est censée s'arrêter quand i vaut 7. Seulement que se passe-t-il lorsque i vaut 7 justement ? L'instruction if teste si 7 est plus petit ou égal à 6 (Faux) et si T(7) est différent de zéro. Or T(7) n'existe pas ! Ce code va donc planter notre programme. Nous devons être plus précis et ne tester T(i) que si la première condition est remplie. Ca ne vous rappelle rien ? Alors regardez le code ci-dessous :

1
2
3
4

while i <= 6 and then T(i) /= 0 loop
   T(i) := 0 ; 
   i := i + 1 ; 
end loop ;

Il faut donc remplacer l'instruction AND par AND THEN. Ainsi, si le premier prédicat est faux, alors le second ne sera pas testé. Cette méthode vous revient maintenant ? Nous l'avions abordée lors du chapitre sur les booléens. Peux être sera-t-il temps d'y rejeter un œil si jamais vous aviez lu les suppléments en diagonale.

Attributs pour les tableaux

Toutefois, pour parcourir un tableau, la meilleure solution est, de loin, l'usage de la boucle FOR. Et nous pouvons même faire encore mieux. Comme nous pourrions être amenés à modifier la taille du tableau ou sa numérotation, voici un code plus intéressant encore :

1
2
3

for i in T'range loop
   T(i) := 0 ; 
end loop ;

L'attribut T'range indiquera l'intervalle de numérotation des cases du tableau : 1..6 pour l'instant, ou 0..5 si l'on changeait la numérotation par exemple. Remarquez que l'attribut s'applique à l'objet T et pas à son type T_Tableau. De même, si vous souhaitez afficher les valeurs contenues dans le tableau, vous devrez écrire :

1
2
3

for i in T'range loop
   put(T(i)) ; 
end loop ;

Voici deux autres attributs liés aux tableaux et qui devraient vous servir : T'first et T'last. T'first vous renverra le premier indice du tableau T ; T'last renverra le dernier indice du tableau. Si les indices de votre tableau vont de 1 à 6 alors T'first vaudra 1 et T'last vaudra 6. Si les indices de votre tableau vont de 0 à 5 alors T'first vaudra 0 et T'last vaudra 5. L'attribut T'range quant à lui, équivaut à écrire T'first..T'last.

Il peut arriver (nous aurons le cas dans les exercices suivants), que vos boucles aient besoin de commencer à partir de la deuxième case par exemple ou de s'arrêter avant la dernière. Auquel cas, vous pourrez écrire :

1
2

for i in T'first +1 .. T'last - k loop
...

Dernier attribut intéressant pour les tableaux : T'length. Cet attribut renverra la longueur du tableau, c'est à dire son nombre de cases. Cela vous évitera d'écrire : T'last - T'first +1 ! Par exemple, si nous avons le tableau suivant :

Les attributs nous renverront ceci :

Tableaux multidimensionels

Tableaux bidimensionnels

Intérêt

Compliquons notre exercice : nous souhaitons enregistrer les scores de 4 équipes de 6 personnes. Nous pourrions faire un tableau unidimensionnel de 24 cases, mais cela risque d'être compliqué de retrouver le score du 5ème joueur de le 2ème équipe Et c'est là qu'arrivent les tableaux à 2 dimensions ou bidimensionnels ! Nous allons ranger ces scores dans un tableau de 4 lignes et 6 colonnes.

Le 5ème joueur de la 2ème équipe a obtenu le score 3 (facile à retrouver).

Déclaration

La déclaration se fait très facilement de la manière suivante :

1

type T_Tableau is array(1..4,1..6) of natural ;

Le premier intervalle correspond au nombre de lignes, le second au nombre de colonnes.

Affectation

L'affectation directe donnerait :

1
2
3
4

Scores := ((15,45,27,8,19,27),
           (41,5,3,11,3,54),
           (12,13,14,19,0,20),
           (33,56,33,33,42,65)) ;

On voit alors que cette méthode, si pratique avec des tableaux unidimensionnels devient très lourde avec une seconde dimension. Quant à l'affectation valeur par valeur, elle exigera d'utiliser deux boucles imbriquées :

1
2
3
4
5

for i in 1..4 loop
   for j in 1..6 loop
      T(i,j) := 0 ; 
   end loop ; 
end loop ;

Tableaux tridimensionnels et plus

Vous serez parfois amenés à créer des tableaux à 3 dimensions ou plus. La déclaration se fera tout aussi simplement :

1
2

type T_Tableau3D is array(1..2,1..4,1..3) of natural ; 
type T_Tableau4D is array(1..2,1..4,1..3,1..3) of natural ;

Je ne reviens pas sur l'affectation qui se fera avec trois boucles FOR imbriquées, l'affectation directe devenant compliquée et illisible. Ce qui est plus compliqué, c'est de concevoir ces tableaux. Voici une illustration d'un tableau tridimensionnel :

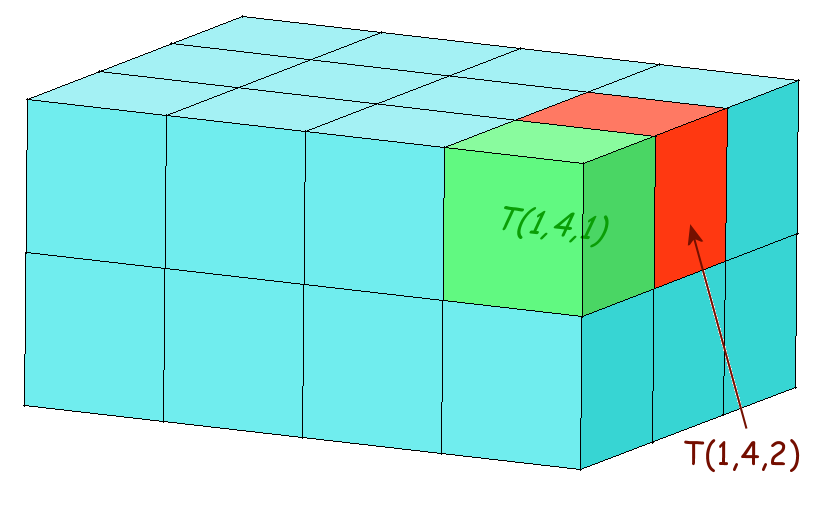
Notre tableau est en 3D, c'est un pavé droit (parallélépipède rectangle) découpé en cases cubiques. T(1,4,2) est donc le cube qui se trouve dans la première ligne, dans la 4ème colonne et dans la 2ème «rangée». Les choses se corsent encore pour un tableau en 4 dimensions, il faut s'imaginer avoir une série de tableaux en 3D (la quatrième dimension jouant le rôle du temps) :

T(1,4,1,2) est donc le cube situé à la 1ère ligne, 4ème colonne, 1ère rangée du 2ème pavé droit.

Et mes attributs ?

Nous avons effectivement un souci. T_Tableau3D est un type de tableau avec 2 lignes, 4 colonnes et 3 rangées, donc quand nous écrivons T'range cela correspond à l'intervalle 1..2 ! Pas moyen d'avoir les intervalles 1..4 ou 1..3 ? Eh bien si ! Il suffit d'indiquer à notre attribut de quelle dimension nous parlons. Pour obtenir l'intervalle 1..4 il faut écrire T'range(2) (l'intervalle de la seconde dimension ou le second intervalle), pour obtenir l'intervalle 1..3 il faut écrire T'range(3) (l'intervalle de la troisième dimension ou le troisième intervalle). Donc T'range signifie en fait T'range(1) !

Et mes agrégats ?

Voici une manière d'initialiser un tableau bidimensionnel de 2 lignes et 4 colonnes :

1

T := (1 => (0,0,0,0), 2 => (0,0,0,0)) ;

On indique que la ligne 1 est (0,0,0,0) puis même chose pour la ligne 2. On peut aussi condenser tout cela :

1

T := (1..2 => (0,0,0,0)) ;

Ou encore :

1

T := (1..2 => (1..4 => 0)) ;

Il devient toutefois clair que les agrégats deviendront vite illisibles dès que nous souhaiterons manipuler des tableaux avec de nombreuses dimensions.

Des tableaux un peu moins contraints

Un type non-contraint ou presque

Vous devriez commencer à vous rendre compte que les tableaux apportent de nombreux avantages par rapport aux simples variables. Toutefois, un problème se pose : ils sont contraints. Leur taille ne varie jamais, ce qui peut être embêtant. Reprenons l'exemple initial : nous voudrions utiliser un tableau pour enregistrer les scores des équipes. Seulement nous voudrions également que notre programme nous laisse libre de choisir le nombre de joueurs et le nombre d'équipes. Comment faire ? Pour l'heure, la seule solution est de construire un type T_Tableau suffisamment grand (500 par 800 par exemple) pour décourager quiconque de vouloir dépasser ses capacités (il faut avoir du temps à perdre pour se lancer dans une partie avec plus de 500 équipes de plus de 800 joueurs ). Mais la plupart du temps, 80% des capacités seront gâchées, entraînant une perte de mémoire considérable ainsi qu'un gâchis de temps processeur. La solution est de créer un type T_Tableau qui ne soit pas précontraint. Voici une façon de procéder avec un tableau unidimensionnel :

1

type T_Tableau is array (integer range <>) of natural ;

Notre type T_Tableau est ainsi «un peu» plus générique.

Attention ! Ici, c'est le type T_Tableau qui n'est pas contraint. Mais les objets de type T_Tableau devront toujours être contraints et ce, dès la déclaration. Celle-ci s'effectuera ainsi :

1
2
3
4

T : T_Tableau(1..8) ; 
   -- OU
N : natural := 1065 ; 
Tab : T_Tableau(5..N) ;

Affectation par tranche

D'où l'intérêt d'employer les attributs dans vos boucles afin de disposer de procédures et de fonctions génériques (non soumises à une taille prédéfinie de tableau). Faites toutefois attention à la taille de vos tableaux, car il vous sera impossible d'écrire T := Tab ; du fait de la différence de taille entre vos deux tableaux Tab et T.

Heureusement, il est possible d'effectuer des affectations par tranches (slices en Anglais). Supposons que nous ayons trois tableaux définis ainsi :

1
2
3

T : T_Tableau(1..10) ; 
U : T_Tableau(1..6) ; 
V : T_Tableau(1..4) ;

Il sera possible d'effectuer nos affectations de la façon suivante :

1
2

T(1..6) := U ;
T(7..10) := V ;

Ou même, avec les attributs :

1
2

T(T'first..T'first+U'length-1) := U ;
T(T'first+U'length..T'first+U'length+V'length-1) := V ;

Déclarer un tableau en cours de programme

Mais cela ne répond toujours pas à la question : «Comment créer un tableau dont la taille est définie par l'utilisateur ?». Pour cela, vous allez devori sortir temporairement du cadre des tableaux et vous souvenir de ce dont nous avions parler dans le chapitre sur les variables et leur déclaration. Lors des compléments, nous avions vu le bloc de déclaration. L'instruction DECLARE va nous permettre de déclarer des variables en cours de programme, et notamment des tableaux. Voici un exemple :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

procedure main is
    n : Integer ;
    type T_Tableau is array (integer range <>) of integer ;
begin
   Put("Quelle est la longueur du tableau ? ") ;
   get(n); skip_line ;

   declare
      tab : T_Tableau(1..n) ;
   begin

      --instructions ne nous intéressant pas

   end;

end main;

Ainsi, nous saisissons une variable n, puis avec DECLARE, nous ouvrons un bloc de déclaration nous permettant de créer notre tableau tab à la longueur souhaitée. Puis, il faut terminer les déclarations et ouvrir un bloc d'instruction avec BEGIN. Ce nouveau bloc d'instructions se terminera avec le END ;.

Quelques exercices

Voici quelques exercices pour mettre en application ce que nous venons de voir.

Exercice 1

Énoncé

Créez un programme Moyenne qui saisit une série de 8 notes sur 20 et calcule la moyenne de ces notes. Il est bien sûr hors de question de créer 8 variables ni d'écrire une série de 8 additions car le programme devra pouvoir être modifié très simplement pour pouvoir calculer la moyenne de 7, 9, 15… notes, simplement en modifiant une variable !

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

with Ada.Text_IO, Ada.Integer_Text_IO, Ada.Float_Text_IO ;
use Ada.Text_IO, Ada.Integer_Text_IO, Ada.Float_Text_IO ;

procedure Moyenne is
   Nb_Notes : constant integer := 8 ;               --Constante donnant la taille des tableaux
   type T_Tableau is array(1..Nb_notes) of float ;  --type tableau pour enregistrer les notes
   Notes : T_Tableau ;                              --tableau de notes
   Moy : float ;                                    --variable servant à enregistrer la moyenne

   function saisie return T_Tableau is              --fonction effectuant la saisie des valeurs d'un tableau
      T : T_Tableau ; 
   begin
      for i in T'range loop
         Put("Entrez la ") ; Put(i,1) ; 
         if i=1
            then put("ere note : ") ; 
            else put("eme note : ") ; 
         end if ; 
         get(T(i)) ; skip_line ; 
      end loop ; 
   return T ; 
   end saisie ; 

   function somme(T:T_Tableau) return float is       --fonction effectuant la somme des valeurs contenues dans un tableau
      S : float := 0.0 ; 
   begin
      for i in T'range loop
         S:= S + T(i) ; 
      end loop ; 
   return S ; 
   end somme ; 

begin                                                --Procédure principale
   Notes := saisie ; 
   Moy := Somme(Notes)/float(Nb_Notes) ; 
   Put("La moyenne est de ") ; Put(Moy) ; 
end Moyenne ;

1

Put(Moy,2,2,0) ;

Exercice 2

Énoncé

Rédigez un programme Pascal qui affichera le triangle de Pascal jusqu'au rang 10. Voici les premiers rangs :

1
2
3
4
5
6

1
1  1
1  2  1
1  3  3  1
1  4  6  4  1
1  5 10 10  5  1

Ce tableau se construit de la manière suivante : pour calculer une valeur du tableau, il suffit d'additionner celle qui se trouve au dessus et celle qui se trouve au-dessus à gauche. Le triangle de Pascal est très utile en Mathématiques.

Comme on ne peut créer de tableaux «triangulaires», on créera un tableau «carré» de taille 10 par 10 rempli de zéros que l'on n'affichera pas. On prendra soin d'afficher les chiffres des unités les uns en dessous des autres.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

with Ada.Text_IO,Ada.Integer_Text_IO ; 
use Ada.Text_IO,Ada.Integer_Text_IO ; 

procedure Pascal is
   Taille : constant integer := 10 ; 
   type T_Tableau is array(1..Taille, 1..Taille) of integer ; 
   Pascal : T_Tableau ; 

   function init return T_Tableau is
      T : T_Tableau ; 
   begin
      T := (others => 0)
   return T ; 
   end init ; 

   function CreerTriangle (Tab : T_Tableau) return T_Tableau is
      T : T_Tableau := Tab ;    --comme on ne peut pas modifier le paramètre, on en crée une copie
   Begin
      for i in T'range loop 
         T(i,1) := 1 ;          --le premier nombre vaut toujours 1
         for j in 2..i loop     --on remplit ensuite la ligne à partir du deuxième nombre
            T(i,j) := T(i-1,j) + T(i-1,j-1) ; 
         end loop ; 
      end loop ;
   Return T ; 
   end CreerTriangle ;

   Procedure Afficher(T : T_Tableau) is
   begin
      for i in T'range loop
         for j in 1..i loop 
            Put(T(i,j),4) ; 
         end loop ; 
         new_line ; 
      end loop; 
   end Afficher ; 
      

begin

   Pascal := init ; 
   Pascal := CreerTriangle(Pascal) ; 
   Afficher(Pascal) ; 

end Pascal ;

1
2
3
4
5
6
7
8

for i in T'range loop
   for j in 1..i loop     --on remplit ensuite la ligne à partir du deuxième nombre
      if i = 1
         then T(i,j) := 1 ;
         else T(i,j) := T(i-1,j) + T(i-1,j-1) ; 
      end if ; 
   end loop ; 
end loop ;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

function init return T_Tableau is
Begin
   for i in T'range loop 
      T(i,1) := 1 ;          --le premier nombre vaut toujours 1
      for j in 2..i loop     --on remplit ensuite la ligne à partir du deuxième nombre
         T(i,j) := T(i-1,j) + T(i-1,j-1) ; 
      end loop ; 
      for j in i+1 .. T'last loop --on complète avec des 0
         T(i,j) := 0 ; 
      end loop ; 
   end loop ;
Return T ; 
end init ;

Exercice 3

Énoncé

Réalisez un programme TriTableau qui crée un tableau unidimensionnel avec des valeurs entières aléatoires, l'affiche, trie ses valeurs par ordre croissant et enfin affiche le tableau une fois trié.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

With ada.Text_IO, Ada.Integer_Text_IO,Ada.Numerics.Discrete_Random ; 
Use ada.Text_IO, Ada.Integer_Text_IO ; 

Procedure TriTableau is

   Taille : constant natural := 12 ; 
   Type T_Tableau is array(1..Taille) of integer ; 

   --init renvoie un tableau à valeurs aléatoires

   function init return T_Tableau is
      T:T_Tableau ; 
      subtype Intervalle is integer range 1..100 ; 
      package Aleatoire is new Ada.numerics.discrete_random(Intervalle) ; 
      use Aleatoire ; 
      Hasard : generator ; 
   begin
      Reset(Hasard) ; 
      for i in T'range loop 
         T(i) := random(Hasard) ; 
      end loop ; 
   return T ; 
   end init ; 

   --Afficher affiche les valeurs d'un tableau sur une même ligne

   procedure Afficher(T : T_Tableau) is
   begin
      for i in T'range loop
         Put(T(i),4) ; 
      end loop ; 
   end Afficher ; 

   --Echanger est une procédure qui échange deux valeurs : a vaudra b et b vaudra a

   procedure Echanger(a : in out integer ; b : in out integer) is
      c : integer ; 
   begin 
      c := a ; 
      a := b ; 
      b := c ; 
   end Echanger ; 

   --Rangmin cherche la valeur minimale dans une partie d'un tableau ; du rang debut au rang fin
   --Elle ne renvoie pas le minimum mais son rang, son indice dans le tableau

   function RangMin(T : T_Tableau ; debut : integer ; fin : integer) return integer is 
      Rang : integer := debut ; 
      Min : integer := T(debut) ; 
   begin
      for i in debut..fin loop
         if T(i)<Min
            then Min := T(i) ; 
               Rang := i ;
         end if ; 
      end loop ; 
   return Rang ; 
   end RangMin ; 

   --Trier est une fonction qui renvoie un tableau trié du plus petit au plus grand
   --Principe, elle cherche la valeur minimale du tableau et l'échange avec la première valeur
   --puis elle cherche le minimum dans le tableau à partir de la deuxième valeur et l'échange 
   --avec la première valeur, puis elle recommence avec la troisième valeur...

   function Trier(Tab : T_Tableau) return T_Tableau is
      T : T_Tableau := Tab ; 
   begin
      for i in T'range loop
         Echanger(T(i),T(RangMin(T,i,T'last))) ; 
      end loop ; 
   return T ; 
   end Trier ; 

   T : T_Tableau ;

begin
   T := init ; 
   Put_line("Le tableau genere par l'ordinateur est le suivant :") ; 
   Afficher(T) ; New_line ;
   Put_line("Voici le tableau, une fois trie : ") ; 
   Afficher(Trier(T)) ; 
end TriTableau ;

Pour les utilisateurs de la norme Ada2012

Ce que nous venons de voir est valable pour tous les compilateurs, quelle que soit la norme Ada utilisée. En revanche, ce qui va suivre n'est valable que pour les compilateurs intégrant la norme Ada2012. Comme nous l'avions déjà vu lors du chapitre sur les conditions, la nouvelle norme internationale du langage Ada, appelée Ada2012, s'est inspirée des langages fonctionnels. C'est vrai pour les expressions conditionnelles, mais c'est également vrai pour les boucles. Ainsi, la boucle FOR a été enrichie de nouvelles fonctionnalités. La boucle FOR que vous connaissez devrait désormais être nommée FOR IN puisque s'ajoutent désormais trois nouvelles boucles : FOR OF, FOR ALL et FOR SOME.

Boucle FOR OF

La boucle FOR OF est un vrai coup de pouce pour les programmeurs. Aussi appelée foreach dans bon nombre de langages, va appliquer vos instructions à tous les éléments de votre tableau (of = de) sans que vous n'ayez à vous tracasser de leurs indices. Prenons un exemple :

1
2
3
4
5
6
7
8

Procedure Augmente is
   Type T_Tableau is array(1..8) of integer ; 
   T : T_Tableau := (7,8,5,4,3,6,9,2) ; 
begin
   for E of T loop
      E := E + 1 ; 
   end loop ; 
end Augmente ;

Le programme ci-dessus se contente d'incrémenter chacune des valeurs d'un tableau. Mais au lieu d'utiliser une boucle FOR IN comme d'habitude nous utilisons une boucle FOR OF. La variable E n'a pas besoin d'être déclarée, elle est automatiquement créée par la boucle en fonction du type d'éléments contenus dans le tableau T. Vous devez comprendre la phrase « FOR E OF T » ainsi : « Pour chaque élément E de T, faire ceci ou cela ». L'énorme avantage, c'est que nous ne risquons plus de nous tromper dans les indices, Ada prend automatiquement chacun des éléments du tableau. Et si jamais vous aviez un doute sur le typage de E, il est possible de réécrire la boucle ainsi :

1
2
3

for E : Integer of T loop
   E := E + 1 ; 
end loop ;

Encore mieux : la même boucle peut s'appliquer à des tableaux multidimensionnels.

1
2
3
4
5
6
7
8
9

Procedure Augmente is
   Type T_Tableau is array(1..13,1..15,1..32,1..9754) of integer ; 
   T : T_Tableau ; 
begin
   --Initialisez cet énorme tableau vous-même ;-)
   for E of T loop
      E := E + 1 ; 
   end loop ; 
end Augmente ;

Comme vous pouvez le constater, le type T_Tableau ci-dessus est vraiment abominable : très grand et de dimension 4. Normalement, cela nous obligerait à imbriquer quatre boucles FOR IN avec le risque de mélanger les intervalles. Avec la boucle FOR OF, nous n'avons aucun changement à apporter et aucun risque à prendre : Ada2012 gère tout seul.

Expressions quantifiées

Les deux autres boucles (FOR ALL et FOR SOME) ne sont utilisables que pour des expressions, appelées expressions quantifiées. Autrement dit, elles permettent de parcourir notre tableau afin d'y effectuer des tests.

Quantificateur universel

Première expression quantifiée : la boucle FOR ALL, aussi appelée quantificateur universel. Celle-ci va nous permettre de vérifier que toutes les valeurs d'un tableau répondent à un critère précis. Par exemple, nous souhaiterions savoir si tous les éléments du tableau T sont positifs :

1
2
3
4
5
6

...
   Tous_Positifs : Boolean ; 
BEGIN
   ...
   Tous_Positifs := (FOR ALL i IN T'range => T(i) > 0) ; 
   ...

Pour que la variable Tous_Positifs vaille TRUE, tous les éléments de T doivent être positifs. Si un seul est négatif ou nul, alors la variable Tous_Positifs vaudra FALSE. Mais ce code peut encore être amélioré en le combinant avec la boucle FOR OF :

1
2
3
4
5
6

...
   Tous_Positifs : Boolean ; 
BEGIN
   ...
   Tous_Positifs := (FOR ALL e OF T => e > 0) ; 
   ...

L'expression anglaise « for all » peut se traduire en « pour tout » ou « Quel que soit », ce qui est un quantificateur en Mathématiques noté $\forall$. Exprimé à l'aide d'opérateurs booléens, cela équivaudrait à : « (T(1)>0) AND (T(2)>0) AND (T(3)>0) AND (T(4)>0) AND ... ».

Quantificateur existentiel

Poussons le vice encore plus loin. Tant que tous les éléments ne seront pas positifs, nous incrémenterons tous les éléments du tableau. Autrement dit, tant qu'il existe un élément négatif ou nul, on incrémente tous les éléments. Cette dernière phrase, et notamment l'expression « il existe », se note de la façon suivante :

1
2
3

(FOR SOME i IN T'range => T(i) <=0) ; 
      -- OU
(FOR SOME e OF T => e <= 0)

Il s'agit là du quantificateur existentiel. Il suffit qu'un seul élément réponde au critère énoncé pour que l'expression soit vraie. Nous pouvons désormais compléter notre code :

1
2
3
4
5

WHILE (FOR SOME e OF T => e <= 0) LOOP
   FOR e OF T LOOP
      e := e + 1 ; 
   END LOOP ;  
END LOOP ;

L'expression anglaise « for some » peut se traduire en « pour quelques ». Le quantificateur mathématique correspondant est « il existe » et se note $\exists$. Exprimé à l'aide d'opérateurs booléens, cela équivaudrait à : « (T(1)<=0) OR (T(2)<=0) OR (T(3)<=0) OR (T(4)<=0) OR ... ».

Maintenant que vous connaissez les tableaux, notre prochain chapitre portera sur un type similaire : les chaînes de caractères ou string (en Ada). Je ne saurais trop vous conseiller de vous exercer à l'utilisation des tableaux car nous serons amenés à les utiliser très souvent par la suite, et le prochain chapitre ne s'en éloignera guère. Donc s'il vous reste des questions, des zones d'ombre, relisez ce cours et effectuez les exercices. N'hésitez pas non plus à vous fixer des projets ou des TP personnels.

En résumé :

• Pour utiliser des tableaux, vous devez créer un type spécifique en indiquant la taille, le nombre de dimensions et le type des éléments du tableau.
• La manipulation des tableaux se fait généralement à l'aide de boucles afin de traiter les divers éléments. Vous utiliserez le plus souvent la boucle FOR et, si votre compilateur est compatible avec la norme Ada2012, la boucle FOR OF.
• Un tableau est un type composite contraint. Il peut contenir autant d'informations que vous le souhaitez mais vous devez définir sa taille au préalable. Une fois le tableau déclaré, sa taille ne peut plus varier.

• Ada, les types composites
• Sommaire
• Les chaînes de caractères