Variables III : Gestion bas niveau des données

• Algorithmique : tri et complexité
• Sommaire
• La programmation modulaire II : Encapsulation

Le chapitre que nous allons aborder est très théorique et traite de diverses notions ayant trait à la mémoire de l'ordinateur : comment est-elle gérée ? Comment les informations y sont-elles représentées ? Etc. Nous allons passer le plus clair du chapitre à ne pas parler de programmation (étrange me direz-vous pour un cours de programmation ) mais ce n'est que pour mieux revenir sur les types Integer, Character et Float, sur de nouveaux types (Long_Long_Float, Long_Long_Integer… ) ou sur certaines erreurs vues au fil du cours.

Chaque partie de ce chapitre abordera la manière dont l'ordinateur représente les nombres entiers, décimaux ou les caractères en mémoire. Ce sera l'occasion de parler binaire, hexadécimal, virgule flottante… avant de soulever certains problèmes liés à ces représentations et d'en déduire quelques bonnes pratiques.

• Représentation des nombres entiers
• Représentation du texte
• Représentation des nombres décimaux en virgule flottante

Représentation des nombres entiers

Le code binaire

Nous allons essayer, au cours des sections suivantes, de comprendre comment l'ordinateur s'y prend pour représenter les nombres entiers, les caractères ou les nombres décimaux, car cela a des implications sur la façon de programmer. En effet, depuis le début, nous faisons comme s'il était normal que l'ordinateur sache compter de - 2 147 483 648 à 2 147 483 647, or je vous rappelle qu'un ordinateur n'est jamais qu'un amas de métaux et de silicone. Alors comment peut-il compter ? Et pourquoi ne peut-il pas compter au-delà de 2 147 483 647 ? Que se passe-t-il si l'on va au-delà ? Comment aller au delà ? Reprenons tout à la base.

Tout d'abord, un ordinateur fonctionne à l'électricité (jusque là rien de révolutionnaire) et qu'avec cette électricité nous avons deux états possibles : éteint ou allumé.

Bien sûr que non, mais c'est grâce à ces deux états de l'électricité que les Hommes ont pu créer des machines aussi perfectionnées capables d'envoyer des vidéos à l'autre bout du monde. En effet, à chaque état peut-être associé un nombre :

Lorsque le courant passe, cela équivaut au chiffre 1, lorsqu'il ne passe pas, ce chiffre est 0. De même lorsqu'un accumulateur est chargé, cela signifie qu'un 1 est en mémoire, s'il est déchargé, le chiffre 0 est enregistré en mémoire. Nos ordinateurs ne disposent donc que de deux chiffres 0 et 1. Nous comptons quant à nous avec 10 chiffres (0, 1, 2… 8, 9) : on dit que nous comptons en base 10 ou décimale. Les ordinateurs comptent donc en base 2, aussi appelé binaire. Les chiffres 1 et 0 sont appelés bits, pour binary digits c'est à dire chiffre binaire.

Il faut procéder en binaire comme nous le faisons en base 10 : lorsque l'on compte jusqu'à 9 et que l'on a épuisé tous nos chiffres, que fait-on ? On remet le chiffre des unités à 0 et on augmente la dizaine. Eh bien c'est pareil pour le binaire : après 0 et 1, nous aurons donc 10 puis 11. On peut ensuite ajouter une «centaine» et recommencer. Voici une liste des premiers nombres en binaire (je vous invite à essayer de la compléter par vous-même, ce n'est pas compliqué) :

Conversions entre décimal et binaire

Vous aurez remarqué les répétitions : pour les bits des «unités», on écrit un 0 puis un 1, puis un 0… pour les bits des «dizaines», on écrit deux 0 puis deux 1, puis deux 0… pour les bits des «centaines», on écrit quatre 0, puis quatre 1, puis quatre 0… et ainsi de suite en doublant à chaque fois le nombre de 0 ou de 1. Mais il y a une ombre au tableau. Nous n'allons pas faire un tableau allant jusqu'à 2 147 483 647 pour pouvoir le convertir en binaire ! Nous devons trouver un moyen de convertir rapidement un nombre binaire en décimal et inversement.

Conversion binaire vers décimal

Imaginons que nous recevions le signal suivant :

Ce message correspond au nombre binaire 10110 qui se décompose en 0 «unités», 1 «dizaine», 1 «centaine», 0 «millier» et 1 «dizaine de millier». Ce qui s'écrirait normalement :

$10110 = (1 \times 10000) + (0 \times 1000) + (1 \times 100) + (1 \times 10) + (0 \times 1)$ $10110 = (1 \times 10^4) + (0 \times 10^3) + (1 \times 10^2) + (1 \times 10^1) + (0 \times 10^0)$

Il n'y a pas de «dizaines» ou de «centaines» mais plutôt des « deuxaines », « quatraines », « huitaines » … Donc en binaire notre nombre correspond en fait à :

$10110 : (1 \times 2^4) + (0 \times 2^3) + (1 \times 2^2) + (1 \times 2^1) + (0 \times 2^0)$

Ainsi, il suffit donc d'effectuer ce calcul pour trouver la valeur en base 10 de 10110 et de connaître les puissances de deux :

$10110 : (1 \times 16) + (0 \times 8) + (1 \times 4) + (1 \times 2) + (0 \times 1) = 16 + 4 + 2 = 22$

Autre méthode pour effectuer la conversion, il suffit de dresser le tableau ci-dessous. Dans la première ligne, on écrit les puissances de 2 : 1, 2, 4, 8, 16… Dans la seconde ligne, on écrit les bits :

Il y va ainsi une fois 2, plus une fois 4 plus une fois 16 (et 0 fois pour le reste), d'où 22 !

Conversion décimal vers binaire

Imaginons, cette fois que nous souhaitions envoyer en message le nombre 13. Pour cela, nous allons dresser le même tableau que précédemment :

Et posons-nous la question : dans 13 combien de fois 8 ? Une fois bien-sûr ! Et il reste 5. D'où le tableau suivant :

Maintenant, recommençons ! Dans 5 combien de fois 4 ? Une fois et il reste 1 !

Dans 1 combien de fois 2. Zéro fois, logique. Et dans 1 combien de fois 1 : 1 fois.

Donc le nombre 13 s'écrit 1101 en binaire. Le tour est joué.

Retour sur le langage Ada

Représentation des Integer en Ada

Vous avez compris le principe ? Si la réponse est encore non, je vous conseille de vous entraîner à faire diverses conversions avant d'attaquer la suite, car nous n'en sommes qu'au B-A-BA. En effet, les ordinateurs n'enregistre pas les informations bits par bits, mais plutôt par paquets. Ces paquets sont appelés octets, c'est-à-dire des paquets de 8 bits (même s'il est possible de faire des paquets de 2, 4 ou 9 bits).

Pour enregistrer un Integer, le langage Ada utilise non pas un seul mais quatre octets, c'est-à-dire $4 \times 8 = 32$ bits ! Avec un seul bit, on peut coder deux nombres (0 et 1), avec deux bits on peut coder quatre nombres (0, 1, 2, 3), avec trois bits on peut coder huit nombres… avec 32 bits, on peut ainsi coder $2^{32}$ nombres, soit 4 294 967 296 nombres.

Mais la difficulté ne s'arrête pas là. En effet, le plus grand Integer n'est pas 4 294 967 296, mais 2 147 483 647 (c'est-à-dire presque la moitié). Pourquoi ? Tout simplement parce qu'il faut partager ces 4 294 967 296 nombres en deux : les positifs et les négatifs. Comment les distinguer ?

La réponse est simple : tous les Integer commençant par un 0 seront positifs (exemple : 00101001 10011101 10100011 11111001) ; tous les integer commençant par un 1 seront négatifs (exemple : 10101001 10011101 10100011 11111001). Ce premier bit est appelé bit de poids fort. Facile hein ? Eh bien non ! Car il y a encore un problème : on se retrouve avec deux zéros !

00000000 00000000 00000000 00000000 : $+0$ 10000000 00000000 00000000 00000000 : $-0$

C'est dommage et cela complique les opérations d'un point de vue électronique. Du coup, il faut décaler les nombres négatifs d'un cran : le nombre 10000000 00000000 00000000 00000000 correspondra non pas à $- 0$ mais à $- 1$. Le premier 1 signifie que le nombre est négatif, les 31 zéros, si on les convertit en base 10, devraient donner 0, mais avec ce décalage, on doit ajouter 1, ce qui nous donne - 1 !

Conséquence immédiate : l'Overflow et les types long

Patience, je vous entraîne peu à peu dans les méandres de l'informatique afin de mieux revenir sur notre sujet : le langage Ada et la programmation. Cette façon de coder les nombres entiers, qui n'est pas spécifique au seul langage Ada, a deux conséquences. Tout d'abord le plus grand Integer positif est 2 147 483 647 ($2^{31} - 1$), quand le plus petit Integer négatif est - 2 147 483 648 ($2^{31}$) : il y a un décalage de 1 puisque 0 est codé comme un positif et pas comme un négatif par la machine.

Deuxième conséquence, nous n'avons que $2^{32}$ nombres à notre disposition, dont le plus grand est seulement $2^{31} - 1$. C'est très largement suffisant en temps normal, mais pour des calculs plus importants, cela peut s'avérer un peu juste (souvenez-vous seulement des calculs de factorielles). En effet, si vous dépassez ce maximum, que se passera-t-il ? Eh bien plusieurs possibilités. Soient vous y allez façon «déménageur» en rédigeant un code faisant clairement appel à des nombres trop importants :

1
2

n : = 2**525 ; 
p := Integer'last + 1 ;

Et alors, le compilateur vous arrêtera tout de suite par un doux message : value not in range of type "Standard.Integer". Ou bien vous y allez de façon «masquée» ( ), le compilateur ne détectant rien (une boucle itérative ou récursive, un affichage du type Put(Integer'last+1);). Vos nombres devenant trop grands, ils ne peuvent plus être codés sur seulement quatre octets, il y a ce que l'on appelle un dépassement de capacité (aussi appelé overflow [j'adore ce mot ]). Vous vous exposez alors à deux types d'erreurs : soit votre programme plante en affichant une jolie erreur du type suivant.

1

raised CONSTRAINT_ERROR : ###.adb:# overflow check failed

Soit il ne détecte pas l'erreur (c'est ce qui est arrivé avec notre programme de calcul de factorielles) : le nombre positif devient trop grand, il «déborde» sur le bit de poids fort normalement réservé au signe, ce qui explique que nos factorielles devenaient étrangement négatives.

Eh bien le langage Ada a tout prévu. Si les Integer ne suffisent plus, il est possible d'utiliser d'autres types : Long_Integer (avec le package Ada.Long_Integer_Text_IO) et Long_Long_Integer (avec le package Ada.Long_Long_Integer_Text_IO). Les Long_Integer sont codés sur 4 octets soit 32 bits comme les Integer. Pourquoi ? Eh bien cela dépend de vos distributions en fait. Sur certaines plateformes, les Integer ne sont codés que sur 16 bits soit 2 octets d'où la nécessité de faire appel aux Long_Integer. Pour augmenter vos capacités de calcul, utilisez donc plutôt les Long_Long_Integer qui sont codés sur 8 octets soit 64 bits. Ils s'étendent donc de +9 223 372 036 854 775 807 à -9 223 372 036 854 775 808, ce qui nous fait $2^{32}$ fois plus de nombres que les Long_Integer.

Utiliser les bases

En Ada, il est possible de travailler non plus avec des nombres entiers en base 10 mais avec des nombres binaires ou des nombres en base 3, 5, 8, 16… On parlera d'Octal pour la base 8 et d'hexadécimal pour la base 16 (bases très utilisées en Informatique). Par exemple, nous savons que le nombre binaire 101 correspond au nombre 5. Pour cela, nous écrirons :

1
2
3
4

N : Integer ; 
BEGIN
   N := 2#101# ; 
   Put(N) ;

Le premier nombre (2) correspond à la base. Le second (101) correspond au nombre en lui-même exprimé dans la base indiquée : Attention ! En base 2, les chiffres ne doivent pas dépasser 1. Chacun de ces nombres doit être suivi d'un dièse (#). Le souci, c'est que ce programme affichera ceci :

1

5

Il faudra donc modifier notre code pour spécifier la base voulue : Put(N,Base => 2) ; ou Put(N,5,2) ; (le 5 correspondant au nombre de chiffres que l'on souhaite afficher). Votre programme affichera alors votre nombre en base 2.

Il sera possible d'écrire également :

1
2

N := 8#27# --correspond au nombre 7+ 8*2 = 23
N := 16#B#  --en hexadécimal, A correspond à 10 et B à 11

Il est même possible d'écrire un exposant à la suite de notre nombre :

1

N := 2#101#E3 ;

Notre variable N est donc donnée en base 2, elle vaut donc 101 en binaire, soit 5. Mais l'exposant E3 signifie que l'on doit multiplier 5 par $2^3 = 8$. La variable N vaut donc en réalité 40. Ou, autre façon de voir la chose : notre variable N ne vaut pas 101 (en binaire bien sûr) mais 101000 (il faut en réalité ajouter 3 zéros).

Imposer la taille

Imaginez que vous souhaitiez réaliser un programme manipulant des octets. Vous créez un type modulaire T_Octet de la manière suivante :

1

Type T_Octet is mod 2**8 ;

Vous aurez ainsi des nombres allant de 0000 0000 jusqu'à 1111 1111. Sauf que pour les enregistrer, votre programme va tout de même réquisitionner 4 octets. Du coup, l'octet 0100 1000 sera enregsitré ainsi en mémoire : 00000000 00000000 00000000 01001000. Ce qui nous fait une perte de trois octets. Minime me direz-vous. Sauf que si l'on vient à créer des tableaux d'un million de cases de types T_Octets, pour créer un nouveau format de fichier image par exemple, nous perdrons $3 \times 1000000 = 3 Mo$ pour rien. Il est donc judicieux d'imposer certaines contraintes en utilisant l'attribut 'Size de la sorte :

1
2

Type T_Octet is mod 2**8 ; 
For T_Octet'size use 8 ;

Ainsi, nos variables de type T_Octet, ne prendront réellement que 1 octet en mémoire.

Représentation du texte

Avant de nous attaquer à la représentation des décimaux et donc des Float, qui est particulièrement complexe, voyons rapidement celle du texte. Vous savez qu'un String n'est rien de plus qu'un tableau de characters et qu'un Unbounded_String est en fait une liste de Characters. Mais comment sont représentés ces characters en mémoire ? Eh bien c'est très simple, l'ordinateur n'enregistre pas des lettres mais des nombres.

Grâce à une table de conversion. L'exemple le plus connu est ce que l'on appelle la table ASCII (American Standard Code for Information Interchange). Il s'agit d'une table de correspondance entre des characters et le numéro qui leur est attribué. Cette vieille table (elle date de 1961) est certainement la plus connue et la plus utilisée. La voici en détail sur la figure suivante.

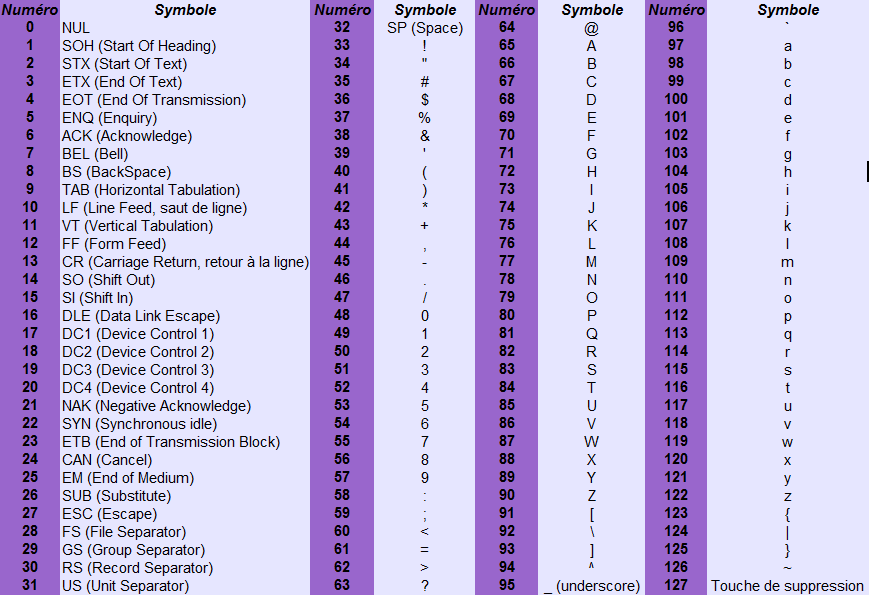
Comme vous pouvez le voir, cette table contient 128 caractères allant de 'A' à 'z' en passant par '7', '#' ou des caractères non imprimables comme la touche de suppression ou le retour à la ligne. Vous pouvez dors et déjà constater que seuls les caractères anglo-saxons sont présents dans cette table (pas de 'ö' ou de 'è') ce qui est contraignant pour nous Français. De plus, cette table ne comporte que 128 caractères, soit $2^7$. Chaque caractère ne nécessite donc que 7 bits pour être codé en mémoire, même pas un octet ! Heureusement, cette célèbre table s'est bien développée depuis 1961, donnant naissance à de nombreuses autres tables. Le langage Ada n'utilise donc pas la table ASCII classique mais une sorte de table ASCII modifiée et étendue. En utilisant le 8ème bit, cette table permet d'ajouter 128 nouveaux caractères et donc de bénéficier de $2^8 = 256$ caractères en tout.

Non, je ne vous ai pas menti et vous ne pouvez pas tout à fait utiliser les caractères accentués comme les autres. Ainsi si vous écrivez ceci :

1
2
3
4
5

...
   C : Character
BEGIN
   C := 'ê' ; Put(C) ; 
...

Vous aurez droit à ce genre d'horreur :

1

Û

Vous devrez donc écrire les lignes ci-dessous si vous souhaitez obtenir un e minuscule avec un accent circonflexe :

1
2
3
4
5

...
   C : Character
BEGIN
   C := Character'val(136) ; Put(C) ; 
...

Enfin, dernière remarque, les caractères imprimés dans la console ne correspondent pas toujours à ceux imprimés dans un fichier texte. Ainsi du caractère N°230 : il vaut 'æ' dans un fichier texte mais 'µ' dans la console. Je vous fournis ci-dessous la liste des caractères tels qu'ils apparaissent dans un fichier texte :

Et tel qu'ils apparaissent dans la console :

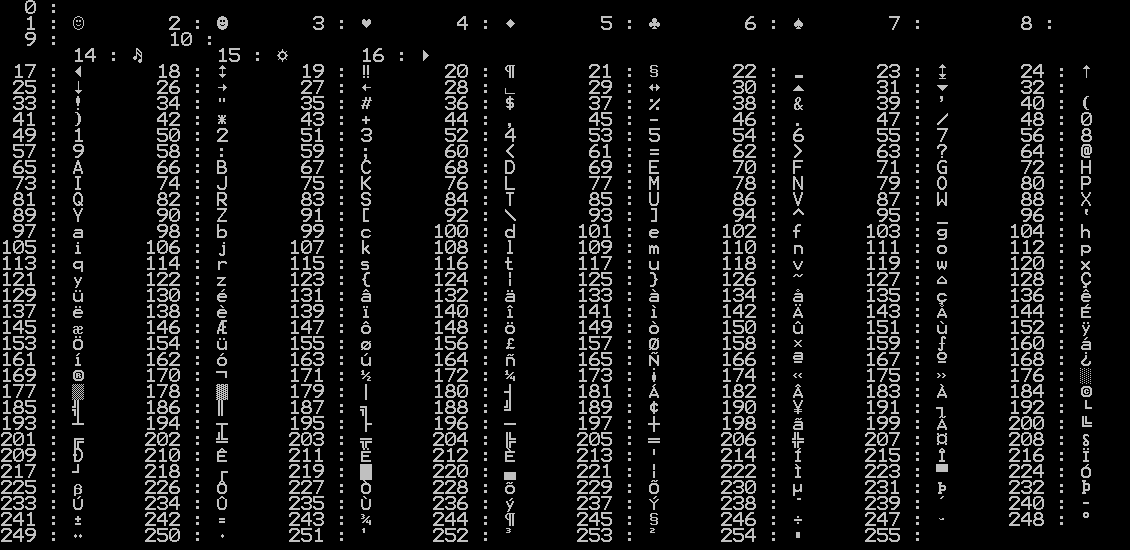
Vous remarquerez les ressemblances avec la table ASCII, mais aussi les différences quant aux caractères spéciaux. Le character n°12 correspond au saut de page et le n°9 à la tabulation.

Représentation des nombres décimaux en virgule flottante

Nous arrivons enfin à la partie la plus complexe. S'il vous paraît encore compliqué de passer du binaire au décimal avec les nombres entiers, je vous conseille de relire la sous-partie concernée avant d'attaquer celle-ci car la représentation des float est un peu tirée par les cheveux. Et vous devrez avoir une notion des puissances de 10 pour comprendre ce qui suit (je ne ferai pas de rappels, il ne s'agit pas d'un cours de Mathématiques).

Représentation des float

Représentation en base 10

Avant toute chose, nous allons voir comment écrire différemment le nombre $- 9876,0123$ dans notre base 10. Une convention, appelée écriture scientifique, consiste à n'écrire qu'un seul chiffre, différent de 0, avant la virgule : $9,8760123$. Mais pour compenser cette modification, il faut multiplier le résultat obtenu par 1000 pour indiquer qu'en réalité il faut décaler la virgule de trois chiffres vers la droite. Ainsi, $- 9876,0123$ s'écrira $- 9,8760123 \times 10^3$ ou même $- 9,8760123 E3$.

Eh oui, par défaut, c'est ainsi que sont représentés les nombres décimaux par l'ordinateur, le E3 signifiant $\times 10^3$. Il suffit donc simplement de modifier l'exposant (le 3) pour décaler la virgule vers la gauche ou la droite : on parle ainsi de virgule flottante.

Représentation en binaire

Cette écriture en virgule flottante prend tout son sens en binaire : pour enregistrer le nombre $- 1001,1$ il faudra enregistrer en réalité le nombre $- 1,0011E3$. Mais comme le chiffre avant la virgule ne peut pas être égale à 0, ce ne peut être qu'un 1 en binaire ! Autrement dit, il faudra enregistrer trois nombres :

• le signe : 1 (le nombre est négatif)
• l'exposant : 11 (pour E3, rappelons que 3 s'écrit 11 en binaire)
• la mantisse : 0011 (on ne conserve pas le 1 avant la virgule, c'est inutile)

D'où une écriture en mémoire qui ressemblerait à cela :

En simple précision, les nombres à virgule flottante sont représentés sur 4 octets. Comment se répartissent les différents bits ? C'est simple.

• D'abord 1 bit pour le signe,
• puis 8 bits pour l'exposant,
• enfin le reste (soit 23 bits) pour la mantisse.

Sauf que l'exposant, nous venons de le voir peut être négatif et qu'il ne va pas être simple de gérer des exposants négatifs comme nous le faisions avec les Integer. Pas question d'avoir un bit pour le signe de l'exposant et 7 pour sa valeur absolue ! Le codage est un peu plus compliqué : on va décaler. L'exposant pourra aller de -127 à +128. Si l'exposant vaut 0000 0000, cela correspondra au plus petit des exposants : $- 127$. Il y a un décalage de 127 par rapport à l'encodage normal des Integer.

Un exemple

Nous voulons convertir le nombre 6,75 en binaire et en virgule flottante. Tout d'abord, convertissons-le en binaire :

$6,75 = ({\color{red}1} \times 2^2) + ({\color{red}1} \times 2^1) + ({\color{red}0} \times 2^0) + ({\color{red}1} \times 2^{-1}) + ({\color{red}1} \times 2^{-2})$

Donc notre nombre s'écrira 110,11. Passons en écriture avec virgule flottante : $1,1011\times 2^2$ ou $1,1011E2$. Rappelons qu'il faut décaler notre exposant de 127 : $2+127=129$. Et comme 129 s'écrit 10000001 en binaire, cela nous donnera :

Cas particuliers

En effet, ce raisonnement n'est valable que pour des nombres dont l'exposant n'est ni 0000 0000 ni 1111 1111, c'est à dire si les nombres sont normalisés. Dans le cas contraire, on associe des valeurs particulières :

• Exposant 0 Mantisse 0 : le résultat est 0.
• Exposant 0 : on tombe dans le cas des nombres dénormalisés, c'est à dire dont le chiffre avant la virgule est 0 (nous n'entrerons pas davantage dans le détail pour ce cours)
• Exposant 1111 1111 Mantisse 0 : le résultat est l'infini.
• Exposant 1111 1111 : le résultat n'est pas un nombre (Not A Number : NaN).

Remarquez que du coup, pour les flottants, il est possible d'avoir $+0$ et $-0$ ! Bien. Vous connaissez maintenant les bases du codage des nombres flottants (pour plus de précisions, voir le tutoriel de Mewtow), il est grand temps de voir les implications que cela peut avoir en Ada.

Implications sur le langage Ada

De nouveaux types pour gagner en précision

Bien entendu, vous devez vous en doutez, il existe un type Short_Float (mais pas short_short_float), et il est possible de travailler avec des nombres à virgule flottante de plus grande précision à l'aide des types Long_Float (codé sur 8 octets au lieu de 4, c'est le format double précision) et Long_Long_Float (codé sur 16 octets). Vous serez alors amenés à utiliser les packages Ada.Short_Float_IO, Ada.Long_Float_IO et Ada.Long_Long_Float_IO (mais ai-je encore besoin de le spécifier ?).

Problèmes liés aux arrondis

Les nombres flottants posent toutefois quelques soucis techniques. En effet, prenons un nombre de type float. Il dispose de 23 bits pour coder sa mantisse, plus un «bit fantôme» puisque le chiffre avant la virgule n'a pas besoin d'être codé. Donc il est possible de coder un nombre de 24 chiffres, mais pas de 25 chiffres. Par exemple $2^{25} + 1$, en binaire, correspond à un nombre de 26 chiffres : le premier et le dernier vaudront 1, les autres 0. Essayons le code suivant :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

...
   x : Float ; 
Begin
   x := 2.0**25 ; 
   put(integer(x), base => 2) ; new_line ;    --on affiche son écriture en binaire (c'est un entier)
   put(x, exp => 0) ; new_line ;              --et on affiche le nombre flottant

   x := x + 1.0 ;                             --on incrémente
   put(integer(x), base => 2) ; new_line ;    --et rebelote pour l'affichage
   put(x, exp => 0) ; 
...

Que nous renvoie le programme ? Deux fois le même résultat ! Étrange. Pourtant nous avons bien incrémenté notre variable x ! Je vous ai déjà donné la réponse dans le précédent paragraphe : le nombre de bits nécessaire pour enregistrer les chiffres (on parle de chiffres significatifs) est limité à 23 (24 en comptant le bit avant la virgule). Si nous dépassons ces capacités, il ne se produit pas de plantage comme avec les Integer, mais le processeur renvoie un résultat arrondi d'où une perte de précision.

De même, si vous testez le code ci-dessous, vous devriez avoir une drôle de surprise. Petite explication sur ce code : on effectue une boucle avec deux compteurs. L'un est un flottant que l'on augmente de 0.1 à chaque itération, l'autre est un integer que l'on incrémente. Nous devrions donc avoir 1001 itérations et à la fin, n vaudra 1001 et x vaudra 100.1. Logique, non ? Eh bien testez donc ce code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

...
   x := 0.0 ; 
   n := 0 ; 
   while x < 100.0 loop
      x := x + 0.1 ; 
      n := n + 1 ; 
   end loop ; 

   Put("x vaut ") ; put(x,exp=>0) ; new_line ; 
   Put_line("n vaut" & Integer'image(n)) ;

Alors, que vaut n ? 1001, tout va bien. Mais que vaut x ? 100.09904 !!! Qu'a-t-il bien pu se passer encore ? Pour comprendre, il faut savoir que le nombre décimal 0.1 s'écrit approximativement 0.000 1100 1100 1100 1100 1100 en binaire… Cette écriture est infinie, donc l'ordinateur doit effectuer un arrondi. Si la conversion d'un nombre entier en binaire tombe toujours juste, la conversion d'un nombre décimal quant à elle peut poser problème car l'écriture peut être potentiellement infinie. Et même chose lorsque l'on transforme le nombre binaire en nombre décimal, on ne retrouve pas 0.1 mais une valeur très proche ! Cela ne pose pas de véritable souci lorsque l'on se contente d'effectuer une addition. Mais lorsque l'on effectue de nombreuses additions, ce problème d'arrondi commence à se voir. La puissance des ordinateurs et la taille du type float (4 octets) est largement suffisante pour pallier dans la plupart des cas à ce problème d'arrondi en fournissant une précision bien supérieure à nos besoins, mais cela peut toutefois être problématique dans des cas où la précision est de mise.

Car si cette perte de précision peut paraître minime, elle peut parfois avoir de lourdes conséquences : imaginez que votre programme calcule la vitesse qu'une fusée doive adopter pour se poser sans encombre sur Mars en effectuant pour cela des milliers de boucles ou qu'il serve à la comptabilité d'une grande banque américaine gérant des millions d'opérations à la seconde. Une légère erreur d'arrondi qui viendrait à se répéter des milliers ou des millions de fois pourrait à terme engendrer la destruction de votre fusée ou une crise financière mondiale (comment ça ? Vous trouvez que j'exagère ? ).

Plus simplement, ces problèmes d'arrondis doivent vous amener à une conclusion : les types flottants ne doivent pas être utilisés à la légère ! Partout où les types entiers sont utilisables, préférez-les aux flottants (vous comprenez maintenant pourquoi depuis le début, je rechigne à utiliser le type Float). N'utilisez pas de flottant comme compteur dans une boucle car les problèmes d'arrondis pourraient bien vous jouer des tours.

Delta et Digits

Toujours pour découvrir les limites du type float, testez le code ci-dessous :

1
2
3
4
5
6

...
   x : float ; 
begin
   x:=12.3456789; 
   put(x,exp=>0) ;
...

Votre programme devrait afficher la valeur de x, or il n'affiche que :

1

12.34568

Eh oui, votre type float ne prend pas tous les chiffres ! Il peut manipuler de très grands ou de très petits nombres, mais ceux-ci ne doivent pas, en base 10, excéder 7 chiffres significatifs, sinon … il arrondit ! Ce n'est pas très grave, mais cela constitue encore une fois une perte de précision. Alors certes vous pourriez utiliser le type Long_Float qui gère 16 chiffres significatifs, ou long_long_Float qui en gère 20 ! Mais il vous est également possible en Ada de définir votre propre type flottant ainsi que sa précision. Exemple :

1
2

type MyFloat is digits 9 ; 
x : MyFloat :=12.3456789 ;

Le mot digits indiquera que ce type MyFloat gèrera au moins 9 chiffres significatifs ! Pourquoi "au moins" ? Eh bien parce qu'en créant ainsi un type Myfloat, nous créons un type de nombre flottant particulier utilisant un nombre d'octet particulier. Ici, notre type Myfloat sera codé dans votre ordinateur de sorte que sa mantisse utilise 53 bits. Ce type Myfloat pourra en fait gérer des nombres ayant jusqu'à 15 chiffres significatifs, mais pas au-delà.

Enfin, nous avons beaucoup parlé des nombres en virgule flottante, car c'est le format le plus utilisé pour représenter les nombres décimaux. Mais comme évoqué plus haut, il existe également des nombres en virgule fixe. L'idée est simple : le nombre de chiffres après la virgule est fixé dès le départ et ne bouge plus. Inconvénient : si vous avez fixé à 2 chiffres après la virgule, vous pourrez oubliez les calculs avec 0.00003 ! Mais ces nombres ont l'avantage de permettre des calculs plus rapides pour l'ordinateur. Vous en avez déjà rencontré : les types Duration ou Time sont des types à virgule fixe (donc non flottante). Pour créer un type de nombre en virgule fixe vous procèderez ainsi :

1
2

type T_Prix is delta 0.01 ; 
Prix_CD : T_Prix := 15.99 ;

Le mot clé delta indique l'écart minimal pouvant séparer deux nombres en virgule fixe et donc le nombre de chiffres après la virgule (2 pas plus) : ici, notre prix de 15€99, s'il devait augmenter, passerait à $15,99+0,01 = 16$ €. Une précision toutefois : il est nécessaire de combiner delta avec digits ou range ! Exemple :

1

type T_Livret_A is delta 0.01 digits 6 ;

Toute variable de type T_Livret_A aura deux chiffres après la virgule et 6 chiffres en tout. Sa valeur maximale sera donc 9999.99. Une autre rédaction serait :

1

type T_Livret_A is delta 0.01 range 0.0 .. 9999.99 ;

Toutefois, gardez à l'esprit que malgré leurs limites (arrondis, overflow …) les nombres en virgule flottante demeurent bien plus souples que les nombres en virgule fixe. Ces derniers ne seront utilisés que dans des cas précis (temps, argent …) où le nombre de chiffres après la virgule est connu à l'avance.

En résumé :

• L'encodage du type Integer peut dépendre de la machine utilisée. C'est pourquoi il est parfois utile de définir son propre type entier ou de faire appel au type Long_Long_Integer afin de vous mettre à l'abri des problèmes d'overflow.
• Le type Character gère 256 symboles numérotés de 0 à 255, dont certains ne sont pas imprimables. Les caractères latins sont accessibles via leur position, en utilisant les attributs character'pos() et character'val().
• Le type Float et autres types à virgule flottante, offrent une grande souplesse mais peuvent être soumis à des problèmes d'arrondis.
• Les nombres à virgule fixe sont plus faciles à comprendre mais impliquent beaucoup de restrictions. Réservez-les à quelques types spécifiques dont vous connaissez par avance le nombre maximal de chiffres avant et après la virgule.

• Algorithmique : tri et complexité
• Sommaire
• La programmation modulaire II : Encapsulation